循环流化床炉膛燃烧的数值分析与试验

孙通，辛凯，张全厚

（1.神华（福建）能源有限责任公司 神华福能发电有限责任公司，福建 泉州 362712；2. 哈尔滨电站设备成套设计研究所有限公司，黑龙江 哈尔滨 150046；3.北方重工集团有限公司，辽宁 沈阳 110141）

循环流化床锅炉是在沸腾炉的基础上发展起来的，采用循环流化床的燃烧方式运行，简称CFB 锅炉，由于其具有燃料适用性广、烟气中的污染物排放量低、炉膛内燃烧效率高等显著的优点，目前已被广泛投入使用，未来将向着几十万千瓦级的大型化发展[1]，这方面的研究、开发和运行优化方面也日益受到相关专家学者的重视。

炉膛的燃烧工况对锅炉寿命和电厂整体运行的经济性、安全性等有较大程度的影响，由于流化床锅炉的燃料是颗粒较大的劣质煤，这构成了锅炉受热面磨损的主要因素，另外炉膛上部的受热面长期处在高温高压的状态下，这更加剧了炉膛受热面的磨损程度。现如今电厂趋向大机组大型化，由于设备庞大而复杂，运行中可调节的参数较多，试验不能应对需要而随时进行，加之参数对与之有关的工况影响已不能凭想象和经验做出判断[2]，因此本文采用数值分析与试验的方法，对循环流化床炉膛燃烧进行分析计算。

近年来已有多位学者对炉膛燃烧进行了相关研究，宋景慧、汪涛等[3]对50 MW 生物质循环流化床炉膛进行过二维模拟；张景宪[4]对300 MW 循环流化床锅炉燃烧调整及参数控制进行过分析；曹艳华、涂淑颖[5]对480 t/h 循环流化床锅炉炉膛燃烧温度场进行过分析。由于现场的试验条件有限、试验耗费的周期较长等不利因素的影响，循环流化床锅炉的炉膛燃烧工况很难得到实时的分析，本文运用大型商用CFD 软件FLUENT，基于Simple 算法，运用RNG k-ε 湍流方程，结合有限体积法对控制方程进行离散，在一次风速为25 m/s不变的情况下，针对二次风速分别为40 m/s、50 m/s 工况下的炉膛燃烧进行仿真模拟，并将两种工况下的结果进行对比分析，适时通过试验来验证，为循环流化床锅炉的实际燃烧运行调整和优化设计提供参考依据。

1 模型的建立

1.1 物理模型

循环流化床锅炉的物理模型、结构尺寸及一次风、二次风流动方向如图1 所示，采用solidworks 软件生成。

1.2 数学模型

采用FLUENT 6.3 研究炉膛燃烧，利用gambit 软件建立三维模型和划分网格，根据模型的特点，选择六面体网格，数目为76 万，增加两次网格数目进行无关性检验，得出的误差在合理范围内，最终计算结果的精确性可得到保证。炉膛内的空气流动采用RNG k-ε湍流方程求解，压力速度耦合采用Simple 二阶迎风的离散化算法，将迭代计算的残差精度设置为10-5。

RNG k-ε 模型是由Yakhot 及Orzag 提出的，通过大尺度运动和修正后的粘度项体现小尺度的影响，而使这些小尺度运动有系统地从控制方程中去除，所得到的k 方程和ε 方程，与标准k-ε 模型非常相似。

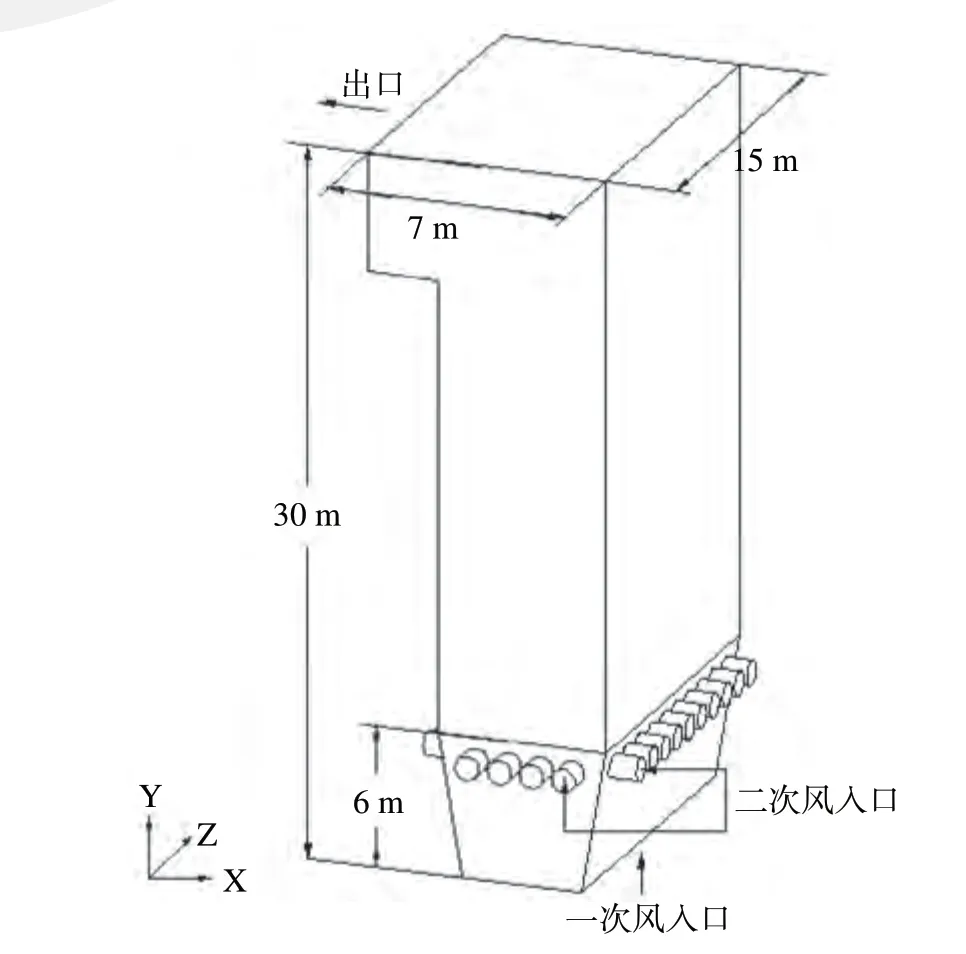
图1 循环流化床锅炉的物理模型

Gk是由层流速度梯度而产生的湍流动能，公式（1）介绍了计算方法；Gb是由浮力而产生的湍流动能，公式（2）介绍了计算方法；YM是由于在可压缩湍流中，过渡的扩散产生的波动；C1ε、C2ε、C3ε是常量，αk和αε是k 方程和ε 方程的湍流Prandtl 数；Sk和Sε是用户定义的。

与标准k-ε模型比较发现，RNG k-ε 模型的主要变化是：

（1）通过修正湍流粘度，考虑了平均流动中的旋转及旋流流动情况。

（2）在ε方程中增加了一项，从而反映了主流的时均应变率eff，这样，RNG k-ε模型中产生项不仅与流动情况有关，而且在同一问题中也还是空间坐标的函数。

从而，RNG k-ε 模型可以更好地处理高应变率及流线弯曲程度较大的流动[6]。

1.3 边界条件

一次风和二次风的边界条件均设置为速度入口，其余设置为壁面边界条件，出口设置为自由出口[7]。

2 结果与分析

2.1 温度场分析

迭代计算收敛后，在z=7.5 m 处建立切片，并进行两种工况的对比性能分析，图2 为针对二次风速分别为40 m/s、50 m/s 情况下的炉膛温度场等值线图。

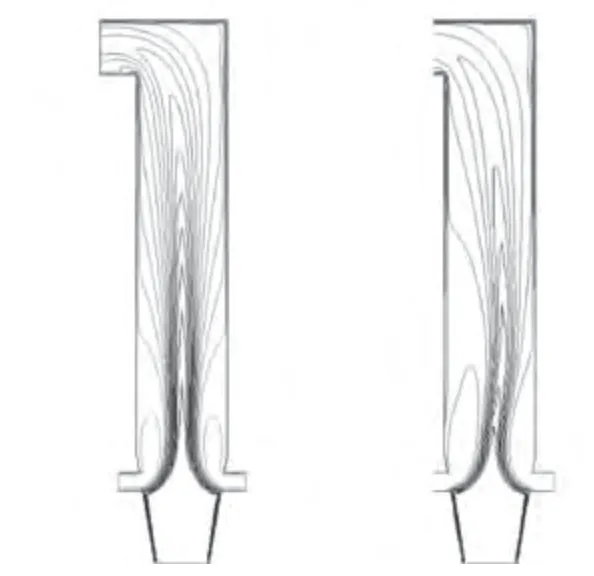
图2 不同二次风速下的炉膛温度场等值线图

由图2 的模拟结果可以看出，在二次风速为40 m/s 和50 m/s 的工况下，炉膛温度场的整体燃烧效果都较为均匀，但在炉膛高度为7 m 时，温度达到最大值，这是因为在此处的燃料较为密集，氧量较大，随着炉膛高度的增大，温度场更加趋近平稳，这是由于氧量和燃料在炉膛中的流动趋近顺畅，二次风速为50 m/s时效果更佳，体现了二次风的助燃作用。

2.2 组分浓度场分析

图3 不同二次风速下的炉膛CO2 分布等值线图

图4 不同二次风速下的炉膛CO 分布等值线图

炉膛内的CO2和CO 含量是反映炉膛内燃烧状况的重要参考依据。由图3 可以看出，当二次风速为40 m/s 时，燃料进入炉膛后与炉膛内的氧气迅速发生燃烧反应，整体CO2的组分分布较为均匀，炉膛中间部分低，向两侧延伸逐渐增高，随着二次风的加大，氧量得到补充，但燃料有向炉膛出口一侧流动的趋势。同理，由图4 可看出，炉膛两侧靠近避免部位发生的燃烧反应较为剧烈，随着二次风的增大，化学反应剧烈，区域偏移。

3 试验分析

为验证模拟的精确性，在现场进行温度场试验分析[8]，在炉膛中取10 个测点，同样保持一次风速恒定不变，二次风速分别设置为40 m/s、50 m/s，每个测点间隔3 min 后，取一组数据，接连取5 组，计算平均值，与FLUENT 中的计算数据进行对比，拟合出曲线图5。

图5 温度场的模拟与试验结果对比

由图5可以看出，FLUENT 的模拟计算值与实测值的拟合曲线分布趋势较为吻合，误差在允许范围内，尤其是临近炉膛空气出口处，其误差主要是由于测量系统偏差、人为操作、模型的简化处理等不可避免的原因引起的[9]。

4 结束语

（1）本文根据现场的运行工况和循环流化床锅炉的实际尺寸，建立出模型，采用FLUENT 软件对调整二次风速后的流场变化进行了分析，解决了试验条件有限、不能适时进行的问题。

（2）通过试验对比分析，可见模拟结果的精确性可靠，可作为循环流化床锅炉的实际燃烧调整和炉膛优化设计提供参考依据。

（3）一次风速恒定不变，随着二次风速的增大，炉壁的燃烧剧烈情况趋近平稳，但综合考虑炉膛实际燃烧运行调解和一二次风配比等因素，在运行和炉膛实际时应酌情考虑。

[1] Yue G X，Yang H R，Lu J F，et al. Latest development of CFB boilers in China[C]//Proceedings of the 20th International Conference on Fluidized Bed Combustion, Springer, 2010.

[2] 廖宏楷，王力. 电站锅炉试验[M]. 中国电力出版社，2007.

[3] 宋景慧，汪涛, 等. 50 MW 生物质循环流化床炉膛燃烧二维模拟[J]. 工业炉，2013,35(3)：8～11.

[4] 张景宪. 300MW 循环流化床锅炉燃烧调整及参数控制分析[J]. 河南科技，2013(12):108.

[5] 曹艳华，涂淑颖, 等.480t/h 循环流化床锅炉炉膛燃烧温度场研究[J]. 电力技术，2013,19(6):69～73.

[6] 王福军 计算流体动力学分析-CFD 软件原理与使用[M]. 北京：清华大学出版社，2004.

[7] 肖琨，王强，刘富君. 基于Fluent 的某型号锅炉末级过热器流动特性数值研究[J]. 能源工程，2011, (3):9～13.

[8] 王鹏利，赵小兵，李连友. 循环流化床锅炉冷态试验方法[J]. 热力发电，2007,(10):27～29.

[9] Zeng Tinghua, Zhan Zhigang. Deep Desulphurization and DeNOx in Circulating Fluidized Bed Boiler[J]. Electricity, 2011,(5):46～49.