基于灵敏度分析的大跨桥梁结构有限元模型优化研究
颜永先,胡 美,李晓娅
(1.浙江舟山跨海大桥有限公司,浙江 舟山 316000;2.浙江省交通科学研究院,杭州 310006)
基于灵敏度分析的大跨桥梁结构有限元模型优化研究
颜永先1,胡 美2,李晓娅2
(1.浙江舟山跨海大桥有限公司,浙江 舟山 316000;2.浙江省交通科学研究院,杭州 310006)
本文给出了一种基于灵敏度分析的大跨桥梁结构有限元模型优化方法。具体步骤如下:(1)通过竣工资料建立有限元模型;(2)利用成桥试验技术报告确定目标函数与修正参数;(3)采用灵敏度分析方法确定修正参数与目标函数的关系,将结构的有限元模型优化问题转化为数学模型的优化问题;(4)采用线性加权法将多目标优化转化为单目标优化问题,并利用二次规划法进行优化求解;(5)用优化后的结果代入有限元模型计算。采用上述方法对金塘大桥主通航孔桥的结构有限元模型进行优化,结果表明:优化后的计算响应值与实测响应值的误差控制在5%以内,验证了上述方法的实用性。
金塘大桥;模型优化;灵敏度分析;构造函数
0 引 言
目前开展大跨桥梁的损伤识别、使用状态评估和预测,一般采用有限元数值模拟分析与大桥检测或健康监测数据相结合的方法。一个比较精确的有限元模型是开展上述工作的基础[1],但是有限元模型的建立是基于结构设计图纸,其中理想化的假定和简化以及实际施工中的误差都将导致结构有限元分析模型计算得到的理论响应与实测响应之间存在一定的偏差。本文依据结构有限元模型优化的一般原理,根据桥梁荷载试验的位移响应测试成果,建立基于灵敏度分析的桥梁结构有限元模型优化方法,使得优化后的结构有限元模型计算的响应值与试验值趋于一致[2]。
1 模型优化方法与原理
在有限元模型优化的实践中,众多学者提出了各种各样的模型优化方法,如:直接修正法、参数修正法、基于仿生优化理论修正法如遗传算法、粒子群算法、模拟退火算法以及蚁群算法等、基于概率统计理论的修正方法、基于神经网络的修正方法、程序本身自带优化功能等。通过对比各种优化方法的优缺点以及适用性[3],本文采用基于灵敏度分析的静力参数修正法对结构有限元模型进行优化。
1.1 目标函数和修正参数
目标函数的选取关系到有限元模型优化成功与否,目前比较常用的是单目标优化函数,而基于位移目标函数的有限元模型优化是静力模型优化中应用得最为广泛的,所以本文根据成桥荷载试验技术报告提供的位移实测数据,采用计算位移与实测位移的残差来构造目标函数。
模型参数误差主要是由不精确的材料、几何参数和边界条件引起[4],根据确定的目标函数,考虑桥梁的结构特点选取修正参数,在选取的过程中要遵循以下两点:(1)不能选取太多参数,否则容易造成求解的病态方程;(2)选择灵敏度较大且较好反映结构损伤位置的参数。
1.2 灵敏度分析
灵敏度分析的算法主要有:差分法、矩阵摄动法、模态综合法和尼尔森法等。本文灵敏度的计算采用有限差分法。扰动步长:Δxi=xi×Δ,xi为修正参数值,Δ的值取0.001。
▽——向后差分算子:
▽f(xi)=f(xi)-f(xi-1)
(1)
向后差分计算表达式:
(2)
其中:P=[P1,P2,…Pn]T,Pn=[P1,P2,…Pk…,Pn]T上式的截断误差与ΔPk同阶。
1.3 构造函数
一般选取的目标函数只体现出模型优化后的最终状态,并没有体现出修正参数与目标量之间的关系。那么在对模型进行优化的过程中就需要构造出修正参数与目标值的关系,首先假设修正参数在初始参数值P0附近发生微小的波动Δp,因波动引起了结构响应值U的变化,利用在初始值附近的一阶泰勒级数展开式来表示结构响应值。结构响应值U与修正参数值P之间的函数关系用下式来表示:
(3)
目标函数即可写成下面的形式:
ΔU=Ua-Ut
(4)
(5)
ΔU=[ΔU1,ΔU2,ΔU3…ΔUj]T
ΔP=[ΔP1,ΔP2,ΔP3…ΔPi]T
(6)
(7)
(8)
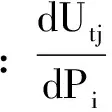
从式(8)可知,f是目标函数,为因变量,ΔPi表示第i个修正参数的增量,是自变量。采用线性加权和法将多目标优化转化为单目标优化问题,有限元模型优化问题即转变为数学模型问题,再利用序列二次规划法(SQP)进行约束优化问题求解。
其中位移计算值U与修正参数P的关系一般为非线性的函数关系,因此P取不同的值时,灵敏度也发生相应的变化[5]。在模型优化过程中,需要不断的更新Sij。当优化好的参数代入模型中得到的模型值与实测值的误差不能满足要求时,需要将优化计算得到的结果代入有限元模型中重新计算灵敏度,再代入式(8)重新计算,每次迭代都需要一次有限元计算和一次灵敏度分析,如此反复最终得到最优结果。
2 背景工程介绍
金塘大桥是舟山跨海大桥五座主桥中最长的一座,是国内继杭州湾跨海大桥、东海大桥之后第三长的跨海大桥。金塘大桥主通航孔桥为主跨620m的五跨钢箱梁斜拉桥,结构总体布置如图1所示,桥跨布置为77m+218m+620m+218m+77m,结构采用半漂浮体系,主梁采用封闭式流线形扁平钢箱梁,箱梁全宽30.1m,中心线梁高3.0m,全桥设置斜拉索84对。
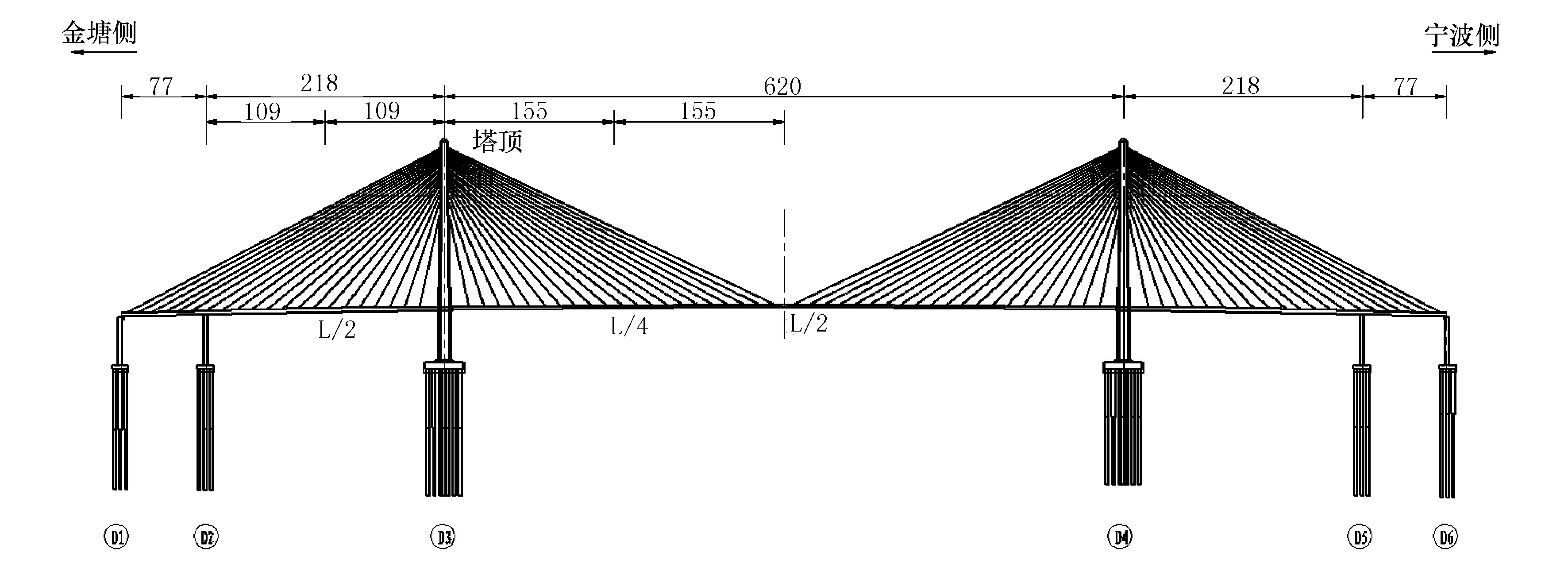
图1 金塘大桥总体布置图
3 模型建立
本文根据金塘大桥的特点和模型优化计算的需要,建立结构有限元模型(如图2)。
(1)主梁为鱼脊梁模型、采用Midas Civil的空间梁单元模拟。这种模型的优点是自由度少、对于抗弯刚度和平动质量处理较精确,可以反映出结构的主要特点。
(2)斜拉索采用只受拉不受压的空间杆单元来模拟,初张力通过在单元中输入初应力实现。斜拉索垂度效应产生的几何非线性采用Ernst公式进行修正。
(3)横梁和塔柱连接处刚性区采用刚性材料法[6]进行模拟,通过提高节点刚性区单元的材料弹性模量,使对应的单元与区域外的单元相比具有“刚性”特点。
(4)支座通过耦合模型中相应的节点自由度来实现。主梁与墩柱之间支座采用弹性连接真实模拟主梁半漂浮结构体系,并且为了更真实的模拟金塘大桥主桥边界条件,模型根据竣工图纸及地质勘察资料建立桩基,采用梁单元模拟,并根据土层特性采用弹簧单元模拟桩-土间相互作用。

图2 金塘大桥模型图
4 模型优化
根据金塘大桥主桥实际位移传感器布置情况,本文选择主梁次边跨跨中、中跨四分点、中跨跨中的竖向位移及主塔塔顶顺桥向水平位移作为目标函数。

其中:Uai为实测位移(成桥荷载报告);Uti为理论位移。
参考相关文献及工程经验,本文重点修正以下五类参数:斜拉索弹性模量、加劲梁弹性模量、加劲梁竖向抗弯惯性矩、主塔弹性模量、主塔竖向抗弯惯性矩,表1规定上述参数的初始值和修正上下限。

表1 修正参数初始值与修正上下限
根据成桥荷载试验活载布置情况,计算目标函数下参数取不同数值的竖向位移,并得到各参数的灵敏度曲线,见图3~图6。下图中横坐标比值表示参数计算值/理论值,纵坐标表示目标函数的位移量。

图3 次边跨跨中灵敏度曲线

图4 中跨四分点灵敏度曲线
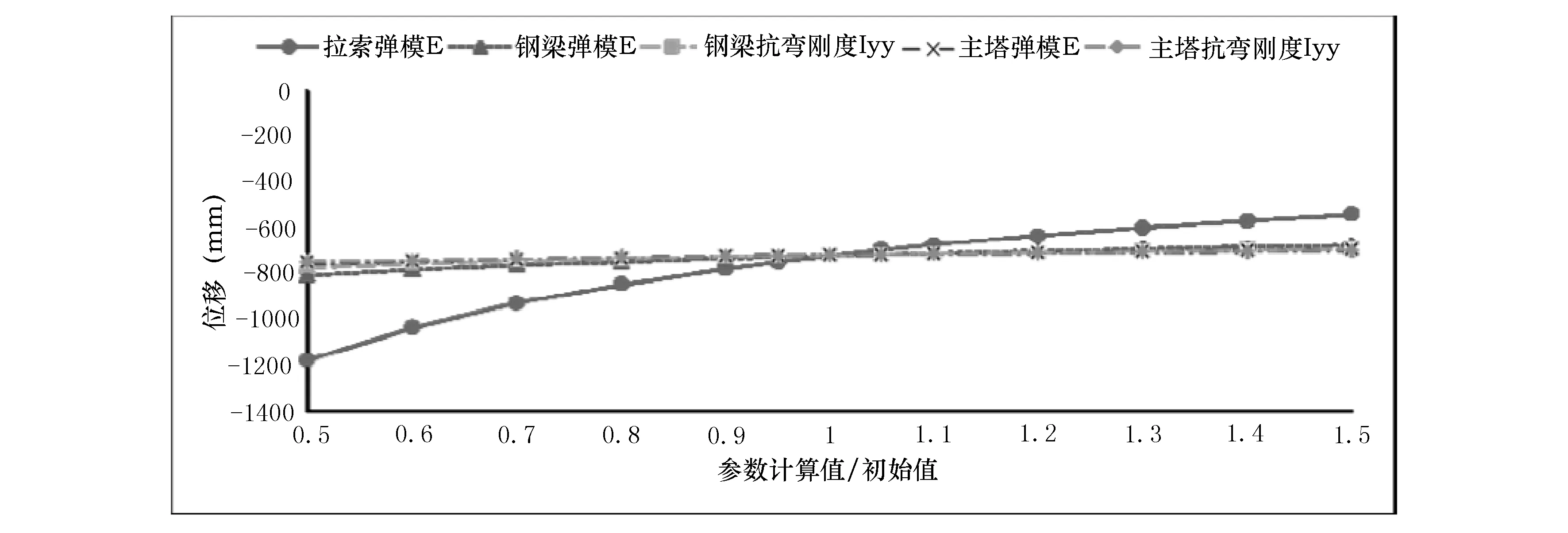
图5 中跨跨中灵敏度曲线

图6 索塔塔顶灵敏度曲线
从以上图形可以看出:
(1)对于次边跨跨中竖向位移、中跨四分点竖向位移、中跨跨中竖向位移,灵敏度从高到低依次为拉索弹性模量、钢梁弹性模量、钢梁竖向抗弯惯矩、主塔弹性模量、主塔抗弯惯矩。
(2)对于主塔塔顶顺桥向水平位移,灵敏度从高到低依次为主塔弹性模量、主塔抗弯惯矩、拉索弹性模量、钢梁弹性模量、钢梁竖向抗弯惯矩。
为进一步求得各参数的灵敏度值,分别将各参数在修正上下限的范围内变化,计算位移值与实测值差值的曲线,进行拟合,得出曲线方程。
①对于次边跨跨中竖向位移,拉索弹模:y=120x-114.4;钢梁弹模:y=44x-38.2;钢梁抗弯惯性矩:y=36x-30.2;主塔弹模:y=20x-34;主塔抗弯惯性矩:y=20x-14。
②对于中跨四分点竖向位移,拉索弹模:y=294x-288.2;钢梁弹模:y=64x-57.2;钢梁抗弯惯性矩:y=40x-33;主塔弹模:y=28x-21;主塔抗弯惯性矩:y=20x-13。
③对于中跨跨中竖向位移,拉索弹模:y=514x-486.4;钢梁弹模:y=118x-88.6;钢梁抗弯惯性矩:y=74x-44.4;主塔弹模:y=54x-24.4;主塔抗弯惯性矩:y=50x-20.2。
④对于主塔塔顶顺桥向水平位移,拉索弹模:y=30x+42.6;钢梁弹模:y=-14x-26.4;钢梁抗弯惯性矩:y=-5x+17.5;主塔弹模:y=-90x+102.6;主塔抗弯惯性矩:y=-90x+102.6。
根据上述求得修正参数的灵敏度汇总见表2所示。利用公式(8)构造参数和目标值的函数关系,采用表2所求灵敏度,荷载试验报告中的位移实测结果,加权系数取1,得到相应的数学模型,并且参考以往工程经验,将理论值与实测值的误差控制在5%以内。利用MATLAB中的fmincon函数对数学模型进行求解,因为在MATLAB中有约束非线性最小化函数fmincon的中型算法使用的是序列二次规划法。求得对应的修正量见表3所示。根据优化结果,代入模型中重新计算可以得出目标函数优化后的数值及误差,见表4所示。可以看出,经优化后,控制点目标位移误差均小于5%,满足目标要求。

表2 活载下各修正参数的灵敏度

表3 活载下各参数修正值

表4 活载下各位移值及其误差
5 结 语
本文采用基于灵敏度分析的静力参数修正方法对金塘大桥模型进行优化,有限元模型更加逼近于实际结构;并且在优化过程中,结构变量始终在预先给定的区间内变化,模型修正结果仍然符合其物理意义,可作为大桥结构健康监测与安全评估的基准有限元模型。上述结果表明:该方法对于大型实际工程结构的优化是可行有效的,且计算过程方便实用,在类似的大跨桥梁结构有限元模型优化分析过程中有借鉴意义。
[1]李兆霞,李爱群,陈鸿天,等.大跨桥梁结构以健康监测和状态评估为目标的有限元模拟[J].东南大学学报:自然科学版,2003,33(5):562-572.
[2]Berman A,Nagy E J.Improvement of a large analytical model using test data[J].AIAA J,1983, 21(8):1168 -1173.
[3] 袁爱民.基于灵敏度分析的有限元模型修正技术若干关键问题研究[D].南京:东南大学,2006.
[4]张启伟.基于环境振动测量值的悬索桥结构动力模型修正[J].振动工程学报,2002,15(1):74-78.
[5]钟颖.基于静力测试数据的桥梁结构有限元模型修正[D].成都:西南交通大学,2009.
[6]杨咏昕,陈艾荣.桥梁结构动力特性分析中节点刚性区问题的处理[J].土木工程学报,2001,(1): 14-18.
Optimization Method for the Finite Element Model of Large Span Bridge Structure Based on Sensitivity Analysis
YAN Yong-xian1, HU Mei2, LI Xiao-ya2
(1. Zhejiang Zhoushan Cross Sea Bridge Co.Ltd., Zhoushan 316000,China; 2.Zhejiang Scientific Research Institute of Transport,Hangzhou 310006,China )
Bringing forward the optimization method for the finite element model of large span bridge structure based on sensitivity analysis. The concrete steps are as follows: (1) the finite element model is established by the completion of data; (2) objective function and parameter modification are determined by the bridge test technology report ; (3) the relationship between parameters and objective function is established by method of sensitivity analysis, the finite element model of the structure optimization problem change into an optimization problem of mathematical model ;(4) using the linear weighted method, the multi-objective optimization change into a single objective optimization problem, and the optimization problem is solved by two quadratic programming method; (5) calculated finite element model with the optimized results .The finite element model of the main navigation span of Jin tang Bridge was optimized by updated method, results show that :the error between the response calculation and the measured response is controlled within 5%, The calculation results prove practicability of the updated method.
Jintang bridge;model optimization;sensitivity analysis;constructed function
2014-04-26
浙江省钱江人才计划项目(2012R10082);浙江省交通投资集团科技项目(201101)
颜永先(1978-),男,湖南益阳人,工程师,硕士,E-mail:464448746@qq.com。
TU311-41
A ?
10.3969/j.issn.1671-234X.2014.03.004
1671-234X(2014)03-0016-06

