基于可靠度的特载车荷载分项系数研究
吕颖钊
(杭州市公路管理局,杭州 310030)
基于可靠度的特载车荷载分项系数研究
吕颖钊
(杭州市公路管理局,杭州 310030)
针对大件运输特载车过桥问题,对特载车荷载分项系数进行研究。根据特载车荷载的特点,确定特载车荷载的概率分布和统计参数。采用概率可靠度方法,对受弯、受剪构件以及6种活恒载比,进行了结构承载能力可靠度计算。以最低可靠指标为尺度,适当考虑了一定的安全余量,推荐了特载车荷载分项系数为1.1。工程应用表明,该系数用于大件运输特载车过桥的结构检算基本可行。
大件运输;荷载分项系数;可靠度方法;最低可靠指标
0 引 言
近年来,随着机械工业的发展和经济建设的需要,盾构机、风叶、变压器、锅炉等大型设备通过公路运输变得越来越频繁。关于公路大件运输的研究,主要集中在大件运输策略[1]、桥梁维修加固[2]、运输设备开发[3]等几个方面,而对于特载车分项系数未有专门研究。《公路工程技术标准》(JTG B01-2003)规定汽车荷载由车道荷载和车辆荷载组成,其中车道荷载用于整体计算,车辆荷载用于局部加载。这种加载模式对特载车过桥的验算不很适用。若要参照,根据《公路桥涵设计通用规范》(JTG D60-2004)中“当某个可变作用在效应组合中其值超过汽车荷载效应时,则该作用取代汽车荷载,其分项系数应采用汽车荷载的分项系数”,那么特载车的分项系数可取1.4。《公路工程技术标准》(JTJ 001-97)规定车辆荷载分为计算荷载和验算荷载,计算荷载如汽车- 超20级,验算荷载如挂车- 120。目前,一些大件运输项目中,特载车过桥的验算采用验算荷载(挂车荷载)的分项系数,即1.1。文献[4]对我国公路桥梁规范中荷载基本组合分项系数取值大小与欧、美国家公路桥梁规范中有关分项系数进行了对比分析,发现我国公路桥梁规范荷载基本组合效应值处于中等水平。鉴于以上情况,针对大件运输车这种偶然荷载过桥的验算,分项系数取多少合适,本文基于可靠度的方法对特载车分项系数进行了专门的研究。
1 恒载效应模型
桥梁结构的恒载属于永久恒载,随时间的变化很小,即使在桥梁加固或维修保养中有所变化,也可以通过现场调查进行确定。但考虑到精确检测桥梁构件的几何尺寸、材料容重等参数并不现实,因此,在可靠度分析时恒载(恒载效应)采用随机变量概率模型进行描述。一般认为恒载(恒载效应)服从正态分布[5]。恒载效应的概率模型、概率分布及统计参数如下:
SG=KGSGk
(1)
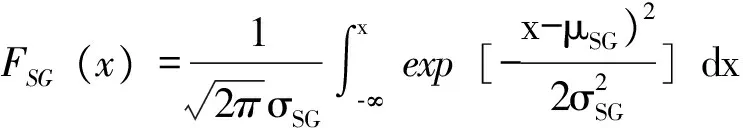
(2)
μSG=κSGSGk
(3)
σSG=μSGδSG
(4)
式中:SGk为恒载效应标准值;μSG,σSG,δSG分别是恒载效应的平均值、标准差和变异系数;KG为考虑恒载效应不定性影响的正态分布随机变量。根据文献[5],恒载效应的统计参数κSG=1.0148,δSG=0.0431。
2 特载车荷载效应模型
2.1 特载车荷载与桥梁规范中汽车荷载的区别
桥梁规范中汽车荷载(如公路-Ⅰ级或汽车-超20级)是经过统计分析的等代荷载,即具有一定可靠度的虚拟荷载。汽车荷载的变异性较大,文献[5]中明确汽车荷载可按照满铺平稳二项随机过程进行分析,荷载大小与设计(评估)基准期有关,设计(评估)基准期内汽车荷载服从极值Ⅰ型分布。汽车荷载过桥时,应考虑冲击系数影响,冲击系数与桥梁跨径有关。
特载车荷载与汽车荷载有较大的不同。第一,特载车荷载是实实在在荷载,其标准值可通过调查实测确定。第二,虽然特载车单车总重很大,但车轴很多、轮胎很密,那么分配到单个车轴或轮胎的压力并不大。第三,由于特载车荷载是真实荷载,且各个车轴的荷载通过油压系统可调节控制的,因此特载车荷载的变异性较小。第四,鉴于荷载真实性特点,确定特载车荷载服从正态分布,且与基准期无关。最后,考虑到特载车过桥一般以很低的速度(不大于10km/h)缓慢匀速通过,且其减震装置的减振缓冲效果要好于一般运输车辆,因此,特载车过桥可不考虑冲击系数影响。
2.2 特载车荷载效应概率模型
尽管大件运输特载车荷载是真实确定的,其荷载大小(轴重、轴距)可以通过实测得到,但是考虑到各个轴载分配的不均匀性和荷载效应计算模式的不精确性等因素影响,将特载车荷载(荷载效应)按照随机变量进行可靠度计算更为合理。结合特载车荷载特点,确定荷载效应的概率模型、概率分布及统计参数如下:
SQ=KQSQk
(5)
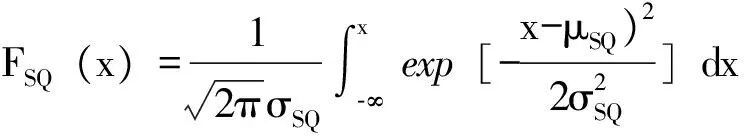
(6)
μSQ=κSQSQk
(7)
σSQ=μSQδSQ
(8)
式中:SQk为通过实测轴距、轴重计算的特载车荷载效应标准值;μSQ,σSQ,δSQ分别为特载车荷载效应的平均值、标准差和变异系数;KQ为考虑特载车荷载效应不定性影响的正态分布随机变量。
大件运输对大件货物的吊装有严格的要求。以钱江隧道盾构设备运输为例,在采用吊机装载时,将盾构设备的重心对准平板挂车的装载中心,并通过平板挂车液压悬挂系统的压力表监测大件货物的装载效果,保证平板挂车左右两侧的压力差值控制在5%之内(如图1)。
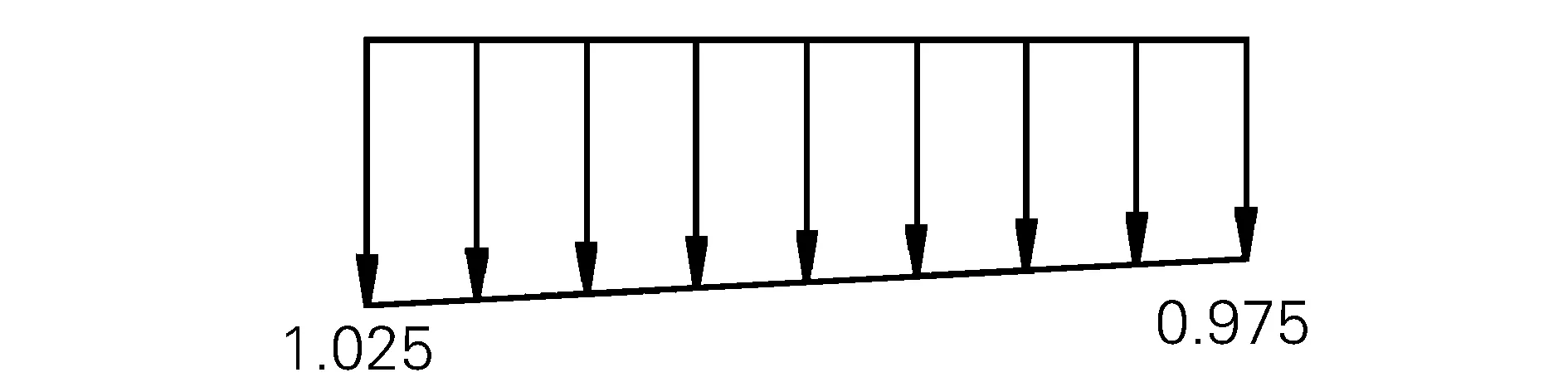
图1 特载车装载后横向不利荷载分布
根据上述横向不利装载图示(均匀分布),特载车荷载效应均值为1,变异系数为0.016。同时,考虑到特载车纵向轴载分配的不均匀性以及特载车过桥轻微冲击的影响[6],并结合钱江隧道盾构设备运输的监测情况,本文建议特载车荷载效应的统计参数κSQ= 1.0,δSQ= 0.05。
3 抗力效应模型
理论上,结构抗力是一个恒定量,但考虑到混凝土材质的不均匀性、结构尺寸的制造与测量误差、抗力计算模式的不精确性等因素的影响,在结构承载能力可靠度分析时,还是将结构抗力作为随机变量考虑。结构抗力效应概率模型为:
R=KRRK
(9)
式中:R为抗力效应概率模型;RK抗力效应标准值;KR为考虑抗力效应不定性影响的对数正态分布随机变量。
根据文献[5],在建立结构抗力与荷载效应关系式的基础上,结构抗力标准值表达式为:
Rk=γ0γR(γGSGk+γQSQk)
(10)
式中:γ0、γR、γG、γQ分别为结构重要性系数、抗力效应分项系数、恒载效应分项系数和特载车荷载效应分项系数;γ0对应于安全等级为一级、二级、三级桥梁分别为1.1、1.0、0.9,这里取值1.0进行研究,即按照特载车通过安全等级为二级桥梁情况进行可靠度分析;γR采用最小二乘法得到的受弯、受剪构件的抗力效应分项系数,如表1所示;γG根据相关规范取1.2;γQ是本文的研究对象,将根据可靠度方法试算确定。

表1 最小二乘法得到的抗力效应分项系数
4 特载车荷载效应分项系数
4.1 极限状态方程
根据可靠度分析方法,构造特载车过桥极限状态方程:
Z=R-SG-SQ
(11)
结合文献[5],抗力效应R、恒载效应SG、特载车荷载效应SQ的统计参数如表2所示。

表2 抗力和荷载效应统计参数表
4.2 最低可靠指标
最低可靠指标,是指特载车过桥时反映人们对桥梁结构安全容忍度的一个指标。理论上,最低可靠指标应根据桥梁结构和大件设备的重要程度、破坏性质、失效后果、经济指标等因素综合分析确定,但实际上目前很难找到一个合适的定量分析方法。我国的可靠度标准[5]采用“校准法”确定结构目标可靠指标。对于安全等级二类桥梁,延性破坏构件的目标可靠指标4.2,脆性破坏构件的目标可靠指标4.7。当条件和依据充分时,可对目标可靠指标进行±0.25幅度的调整。文献[7]提出将最低可靠指标设为β0.25,对应目标可靠指标βT降低0.25水平;文献[8]提出将最低可靠指标设为β0.85βT。另外,还有较多文献对最低可靠指标进行了研究,针对不同的结构,最低可靠指标大多介于2 ~ 4之间,这里不再一一列出。结合大件运输特载车过桥的特点,本文采用最低可靠指标为目标可靠指标下降0.5水平(即延性破坏3.7、脆性破坏4.2)进行结构承载能力可靠度分析。
4.3 可靠度计算
为了全面反映混凝土梁桥的各种受力情况,这里采用受弯、受剪2种受力状态(典型的延性和脆性破坏),活恒载比0.1、0.25、0.5、1、1.5、2.5共6种比值(涵盖大多跨径梁桥),以及初定特载车荷载效应分项系数1.05、1.1、1.15这3种情况,分别进行承载能力可靠度试算。例如:针对受弯构件的活恒载比1、特载车荷载效应分项系数1.1情况,根据式(10)和表1、表2,得到恒载效应的标准值1.0、均值1.0148、标准差0.0437,正态分布;特载车荷载效应的标准值1.0、均值1.0、标准差0.05,正态分布;抗力效应的标准值2.8658、均值3.514、标准差0.497,对数正态分布。再根据改进的JC法进行结构可靠度计算,得到该种情况的结构可靠指标为3.786。限于篇幅,全部情况的计算结果如图2~图5所示。
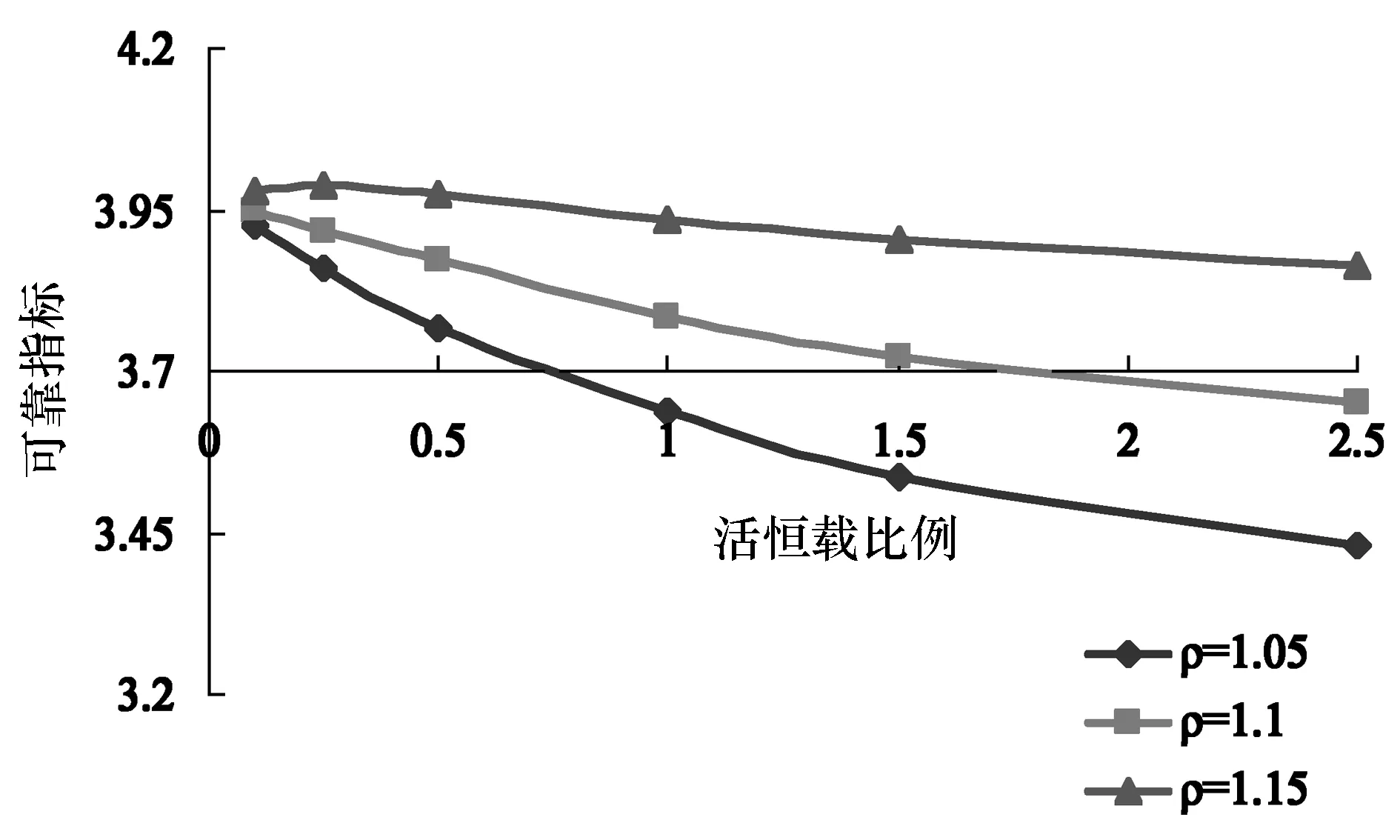
图2 受弯构件可靠度指标计算结果

图3 矩形截面受剪构件可靠度指标计算结果

图4 T形截面受剪构件可靠度指标计算结果

图5 受剪构件可靠度指标计算结果(综合)
4.4γQ讨论
采用活恒载比0.1、0.25、0.5、1、1.5、2.5对应的可靠指标均值和活恒载比0.5、1、1.5对应的可靠指标均值进行分析。关于受弯构件(延性破
坏),在特载车荷载分项系数为1.07时,对应的可靠指标均值约为3.7,满足最低可靠指标要求;当取1.1时,对应的可靠指标均值约为3.8,特载车过桥具有一定安全余量。关于受剪构件(脆性破坏),由于标准中抗力统计参数差异较大,矩形截面与T形截面对应的可靠指标计算结果差距较大,矩形截面的可靠指标低,T形截面的可靠指标高。参考标准中分析方法,采用两种截面对应的可靠指标均值进行综合分析,即使在特载车荷载分项系数为1.05时,结构也满足最低可靠指标要求。
根据上述可靠指标计算结果的讨论,并综合考虑最低可靠指标的模糊性、不同截面构件抗剪可靠指标的差异性、抗弯和抗剪可靠指标的宜统一性等方面因素,本文推荐特载车荷载分项系数为1.1。
5 工程应用
钱江隧道盾构外径15.43 m,是当时世界上最大直径的泥水盾构隧道之一。大件运输时,将盾构机拆分为刀盘驱动、刀盘中心体等十余个大型组件,其中单个运输组件最重为180 t(宽8.04 m)、最宽为8.6 m(167t)。陆路运输的起点为临浦电厂,终点为六工段工地。根据线路调查和最重组件,大件运输单位提供了平板挂车如图6所示,最大轴重控制在16 t。

图6 液压平板挂车图示
沿线经过42座桥梁需要检测评估。通过现场调查,确定旧桥检算系数Z1,并根据前面研究采用特载车荷载效应分项系数1.1,对全部桥梁进行承载能力检算。计算结果为:上部结构承载能力全部满足大件运输要求,下部结构承载能力有7座桥梁(主要是盖梁)不满足大件运输要求。在大件运输之前,根据桥梁缺损情况和检算结果,对其中16座桥梁进行了维修或加固,主要涉及桥面平整度维修、主梁抗裂加固、绞缝局部注浆、盖梁承载力提升、立柱修补等措施。在大件运输过程中,对大跨径桥梁以及调查和检算较差桥梁进行了应力和挠度监测。
盾构大件运输特载车顺利通过42座桥梁,监测数据与理论计算基本吻合,特载车过后桥梁结构未新增明显病害。工程实践表明,采用可靠度方法得出的特载车荷载效应分项系数1.1基本合理。
6 结 语
(1)公路大件运输是一项复杂的系统工程,其中特载车过桥的结构检算是一项重要的工作,鉴于已有规范对特载车荷载分项系数未有明确规定,尽管一些大件运输项目采用挂车荷载分项系数进行桥梁结构承载能力检算,但是规范和理论依据不够充分,因此,有必要以可靠度方法对特载车荷载分项系数进行专门研究。
(2)在分析已有对目标可靠指标、最低可靠指标研究成果的基础上,结合大件运输和桥梁检算特点,本文建议最低可靠指标为目标可靠指标下降0.5水平(即:延性破坏3.7、脆性破坏4.2)。
(3)从分析特载车荷载特点出发,采用可靠度方法,针对受弯和受剪构件以及活恒载比0.1、0.25、0.5、1、1.5、2.5六种情况,对特载车荷载分项系数进行了专门研究,给出了建议值1.1,并在依托工程桥梁结构检算中进行了成功应用。
[1]陈国强,吕颖钊,潘学政.公路大件运输的技术对策[J].浙江交通职业技术学院学报,2010,11(1):5-8.
[2]王学勤.东沙颖河大桥通行大件运输车辆加固技术[J].世界桥梁,2014,42(1):82-86.
[3]刘静,李兴举,黄细洋.大件公路运输桥式车组技术方案设计--以500千伏三堡变电站主变压器运输为例[J].物流技术,2013,(11):269-271.
[4]周勇军,孙婧,梁玉照.公路桥梁设计荷载基本组合的分项系数值及其效应对比[J].公路,2012,1(1):103-107.
[5]GB/T 50283-1999,公路工程结构可靠度设计统一标准[S].
[6]刘波,王有志,王涛,等.大件运输中简支梁桥的动力响应分析及监测[J].哈尔滨工程大学学报,2014,35(3):313-319.
[7]张跃松,王要武,张钟涛.建筑工程结构可靠度与使用寿命的预测及定量关系分析[J].建筑科学,2001,17(4):35-38.
[8]赵国藩.工程结构可靠性理论与应用[M].大连:大连理工大学出版社,1996.
Research on Load Subentry Coefficient of Special Load Vehicles Based on Reliability Method
LV Ying-zhao
(Highway Administration of Hangzhou, Hangzhou 310030, China)
Aiming at special load vehicle through the bridge, load subentry coefficient was researched. According to the characteristics of special load vehicle, the probability distribution and statistical parameters of special vehicle’s load were determined. Referring to the bending member and shear member, and six ratios of live load to dead load, the reliability indexes of bearing capacity were calculated based on reliability method. According to the permissible reliability index and considering the structural safety, the load subentry coefficient 1.1 of special load vehicle was recommended. Engineering application shows that the coefficient 1.1 is feasible for bridge structure checking of large-scale equipment transportation.
large-scale equipment transportation; load subentry coefficient; reliability method; permissible reliability index
2014-05-08
吕颖钊(1978-),男,浙江湖州人,高级工程师,博士,E-mail:lyz117@126.com。
U441.2
A ?
10.3969/j.issn.1671-234X.2014.03.002
1671-234X(2014)03-0005-05

