基于风险的老龄平台检修规划

陈团海， 陈国明， 张 超 ， 曾文彦

(1.中海石油气电集团有限责任公司，北京 100007； 2.中国石油大学海洋油气装备与安全技术研究中心， 山东青岛 266580； 3.中国船级社实业公司武汉分公司， 武汉 430022)

基于风险的老龄平台检修规划

陈团海1， 陈国明2， 张 超1， 曾文彦3

(1.中海石油气电集团有限责任公司，北京 100007； 2.中国石油大学海洋油气装备与安全技术研究中心， 山东青岛 266580； 3.中国船级社实业公司武汉分公司， 武汉 430022)

为确定老龄平台合理的检修方案，建立基于风险的老龄平台检修规划模型。研究模型中检测、维修与失效期望费用的计算方法，采用遗传算法进行优化求解；利用事件树进行概率分析，计算出各检测时间点平台检测、维修与失效三个基本事件的概率；基于规划模型对老龄平台延寿服役期间的检测间隔、方法及维修决策三个参数进行优化。最后以一老龄平台为例，根据备用的检测方法与维修方法确定10种检修方案，采用检修规划模型进行检修优化，结果表明，合理地安排检测与维修能够有效地降低平台风险，维修方法对检修方案的影响大于检测方法。

老龄平台；风险；检修规划；优化；遗传算法

0 引言

老龄平台可定义为达到或者超过其设计寿命的海洋平台，目前世界范围内有大量的老龄平台，由于最初设计不确定性以及经济制约等因素的影响，部分老龄平台仍在继续服役。为保证这些平台延寿服役期的安全性，检测与维修具有非常重要的作用，有效地检测与维修可以降低平台服役期间的风险[1]。因此，对老龄平台制定检修计划时，必须进行合理地规划，使得既能保证平台安全运行，又能最大程度地节省检修费用。老龄平台的检修规划最终可以归结为最优化问题，根据优化对象的不同，分为基于可靠性与基于风险的检修规划，基于风险的检修规划考虑了平台失效与平台维修之间的相对费用，其结果更能应用于工程实际。通常检修规划的具体目标包括四个：(1) 检测时间，包括检测次数与每次检测的时间点；(2) 检测范围，包括检测位置与检测幅度；(3) 检测方法，针对不同位置可能采取不同的检测方法；(4) 维修决策，包括是否维修以及采取的维修方法。该文针对以上问题，建立基于风险的老龄平台检测与维修优化模型，综合考虑各个因素的影响，研究基于风险的老龄平台检修规划。

1 基于风险的老龄平台检修优化模型

风险是指在一定时间内，由于系统行为不确定性产生危害的可能，系统中某一事件的风险可表示为事件发生概率与事件后果严重程度的函数，老龄平台延寿服役期间事件后果严重程度可以用相关费用进行表征，基于平台服役风险的检测与维修优化计算模型可采用下式表示[2]：

(1)

式中：CI(I,R)、CR(I,R)、CF(I,R)和CT(I,R)分别表示平台检测费用、维修费用、失效费用和总费用，I、R分别为检测、维修计划向量；t为服役时间；β(·) 为平台可靠性指标；βmin为可靠性指标下限；Δtmax、Δtmin分别为检测时间最大和最小值；n为检测次数。

在上面的优化模型中，所涉及的各项费用均为期望费用，期望费用可以通过事件概率与事件产生的费用进行计算[3]，优化模型中检测、维修、失效费用可通过下面公式计算。

(1) 检测费用

平台检测的期望费用可表示为[4]：

(2)

式中：CI, i(q)为第i次的检测费用，q为反应检测质量的参数；N为总的检测次数；Ti为第i次的检测时刻，PF(Ti)为时间[0,Ti]内平台失效概率；α为银行利率。

(2) 维修费用

平台维修的期望费用可表示为：

(3)

式中：CR,i(k)表示第i次检测完成后需要维修情况下所对应的维修费用；PR(Ti)为需要维修事件对应的概率。

(3) 失效费用

平台失效对应的期望费用可为：

(4)

式中：CF为平台结构失效对应的损失。

2 基于风险的老龄平台检修优化分析

2.1 平台失效与检修概率计算

进行检修规划时要充分考虑到检测、维修过程中的不确定性，根据概率确定相关事件，对平台检测时能否检测到缺陷由检测方法的检测概率函数决定，检测到缺陷后是否维修根据维修可靠性函数确定，平台维修后的恢复程度与维修方法有关。

2.1.1 失效概率

老龄平台检修与失效概率的计算可以借助于事件树，综合考虑每个时刻的检测、维修与失效三个基本事件，建立如图1所示的检修规划事件树。

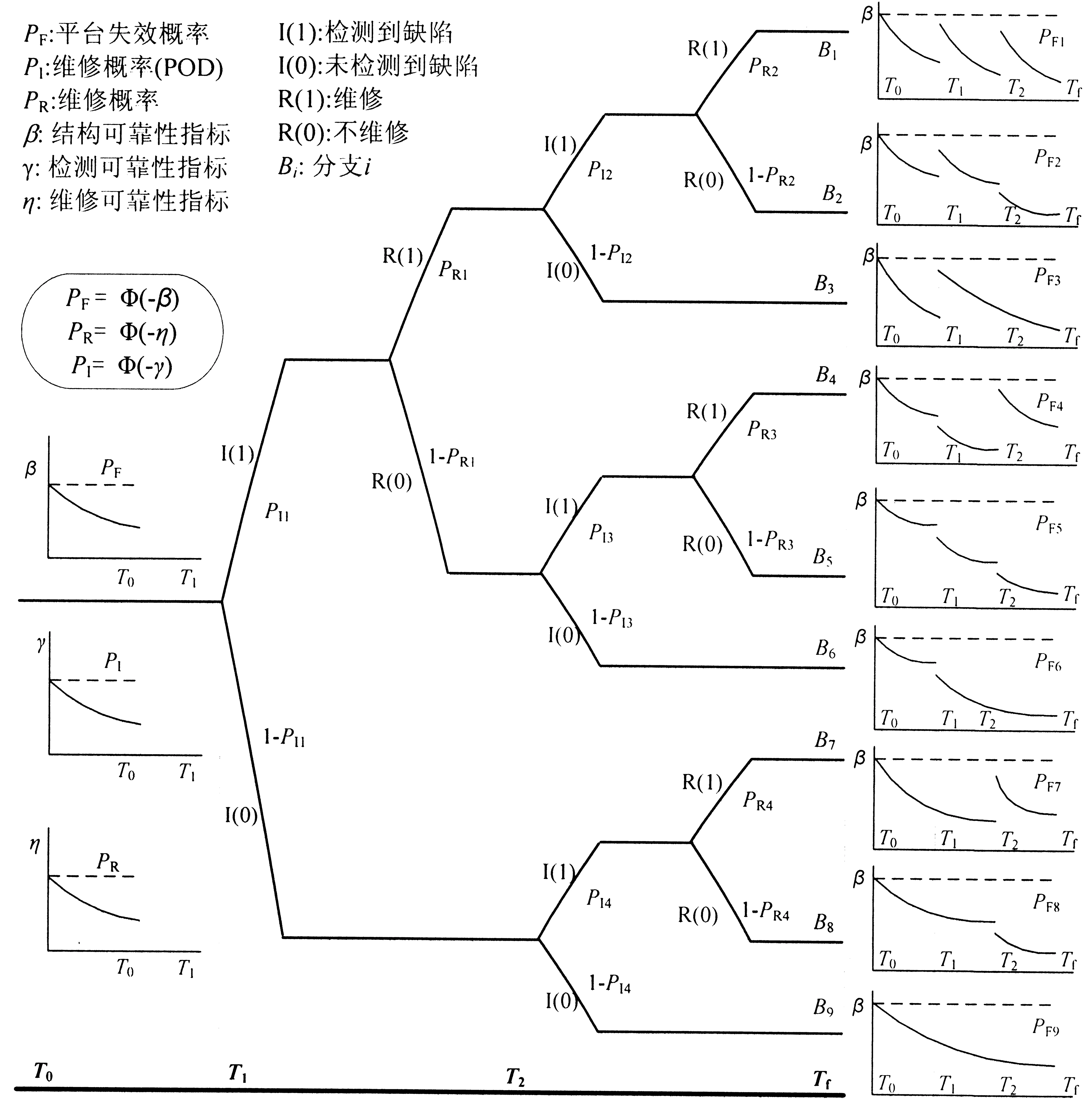
图1 老龄平台检修规划决策事件树

由图1可知：平台第1次检测后事件树有3分支，即未检测到缺陷I(0)、检修到缺陷不需维修I(1)R(0)、检测到缺陷需要维修I(1)R(1)；对平台进行第2次检测时，在第1次检测的3个分支上又各有3个分支，故第2次检测后产生9个分支，以此类推，经过n次检测后，事件树产生3n个分支，平台可靠性与维修可靠性变化曲线也同样有3n种情况。

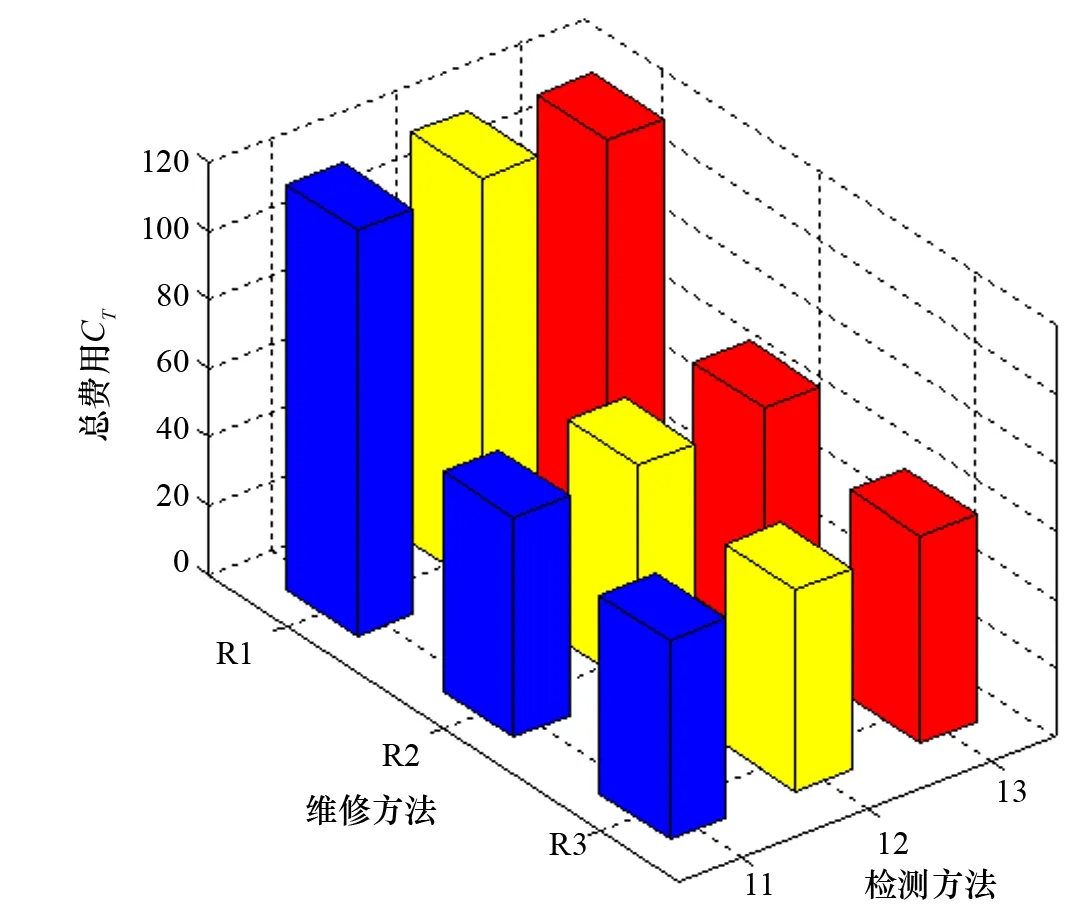
结构从初始时刻至第1次检测时段(T0

式中：MF(t)为时刻t老龄平台结构失效事件安全裕度方程。

根据检修规划决策事件树，老龄平台在时段(T1

(1) 未检测到缺陷

(6)

(2) 检测到缺陷不维修

(7)

(3) 检测到缺陷且维修

(8)

基于以上3分支事件的发生概率，时段(T1

(9)

式(6)～式(9)中：MI(T1)、MR(T1)、MF(T1)分别表示时刻T1平台检测、需要维修以及失效事件的安全裕度；MF0(t)、MF1(t)分别表示未维修、维修1次平台在时刻t失效的安全裕度。维修后，平台维修事件安全裕度和失效事件安全裕度恢复初值，检测事件安全裕度方程往后推T1，即MI1(t)=MI(t-T1)。

采用上面同样方法可得到2、3次检修后平台失效概率的计算公式，限于篇幅，在这不列出。

2.1.2 维修概率

根据图1所示的事件树计算维修概率，结构第1次检测后维修概率为

(10)

第2次检测后维修概率为

(11)

以上即为对老龄平台检修规划时失效概率与维修概率计算公式，可见检修规划时平台的失效和维修概率计算公式比较复杂，平台检测4次后，失效概率计算公式中共有1+34=82项，维修概率也有81项，且在可靠性串联系统各个分支中，最多的基本事件有13个。

2.2 基于遗传算法的优化求解

由式(1)的检修优化模型可知，老龄平台的检修规划求解有两个特点：(1)解空间比较大；(2)优化参数多，且优化参数中检测时间为连续变量，而检测方法与维修方法为离散变量，是一个混合优化问题，采用传统的优化方法难以进行求解，该文选择遗传算法进行优化求解。

遗传算法是一类借鉴生物界进化规律的自适应最优化求解技术。作为一种启发式的全局搜索算法，其主要特点是直接对结构对象进行操作，不受函数必须连续的约束，具有较好的全局优化能力，且对于参数较多的情况可以自适应调整解空间的搜索方法[5-6]，能够有效地解决老龄平台检修规划中的优化问题。

对于本文的最优化问题，可以采用MATLAB优化工具箱中遗传算法实现，n个变量优化可参考如下程序段：

Object_Function=@OPTn; % 确定目标函数

n_var = n; % 确定变量数

LB = [min1 min2 min3 ……]; % 确定下限

UB = [max1 max2 max3 ……]; % 确定上限

Const_Function = @CSTRn; % 指定约束方程

[x, f_val] = ga (Object_Function, n_var, [ ], [ ], [ ], [ ], LB, UB, Const_Function);

根据以上程序段，再进行相应的设置求解即可获得最优解。

3 算例

以某老龄平台为例，该平台于1995年投入使用，设计寿命为15年，目前处于老龄服役期，需要对该平台加强检修，为此根据上面的理论制定该平台延寿服役15年的检修计划。制定计划之前先根据经验制定三种备选检测和维修方法，分别为：

检测方法：I1—PT: 液渗检测；I2—MT: 磁粉探伤；I3—UT: 超声检测。

维修方法：R1—TG:打磨焊趾；R2—GF: 结构灌浆；R3—SC: 结构卡箍。

对所给定的3种检测方法与维修方法进行检修组合，再加上保持不检不修共形成10种平台检修方案，对前面9种方案进行优化求解，计算最低费用；直接通过失效概率计算第10种方案的平台失效损失费用，对两种费用进行对比，确定最优的检修方案。

优化模型中涉及的所有费用采用相对费用表示，3种检测方法之间的相对费用为CPT∶CMT∶CUT=0.5∶1∶2，3种维修方法的相对费用为CTG∶CGF∶CSC=5∶10∶20，以检测方法磁粉探伤、维修方法结构灌浆的费用为相对费用基准，平台失效费用CF0相对检测的费用比例为CMT∶CF0= 1∶5×106、相对维修费用的比例为CGF∶CF0= 1∶5×105。

根据上面参数进行优化求解，确定每种检修方案的最优检测次数以及对应的相对费用，并列出总费用中各单项费用数值，详细结果见表1。

表1 优化结果

备注：表中“- ”表示无该项

图2 维修规划9种方案最优费用三维柱状图

由表1可知，方案10(即平台延寿服役期间不检测、不维修)的费用最高，这说明老龄平台在延寿服役过程中虽然检测和维修要花费大量的费用，但是这个费用是非常必要的。通过比较各方案的总费用可知，方案3为最优检修方案，检修组合为I1-R3，即检测方法选择液渗检测，维修方法选择结构卡箍，服役期内共需要2次检测，检测时刻分别为延寿服役期的第4.5年和9.5年。

根据表1的结果，以三维柱状图表示第1～9种方案(优化方案)的总费用(如图2所示)。由图2可知，采用同一种维修方法时总费用相差不大，而采用同一种检测方法时总费用相差较大，这说明维修方法对总费用的影响远大于检测费用。这是因为对平台检测时只是对平台的状态进行识别，并没有改变平台的状态，而对平台维修时改变了平台本身的结构状态，能够有效地削减平台的服役风险。

在计算中假设平台各项费用成一固定比例，且检测函数与维修效果为确定函数，当费用参数与函数改变时，计算结果与最优方案可能会发生变化；但只要能够确定优化模型中的各参数，均可采用该规划模型进行老龄平台检修优化。

4 结论

(1) 给出了平台检修过程中检测、维修与失效产生的期望费用计算模型，综合考虑可靠性与检测间隔要求，建立了基于风险的老龄平台检修优化模型。

(2) 建立了老龄平台检修规划事件树模型，确定了检修决策过程中每个检测时刻的分支事件，给出了各分支事件的平台结构可靠性与维修概率计算公式，并综合考虑各分支事件本身概率计算了平台最终的失效概率。

(3) 综合考虑平台检修过程中的各不确定因素，采用遗传算法对平台检测与维修进行规划。通过对10种检修方案优化分析发现，检测与维修能够有效地降低平台风险，维修方法对最优方案的确定有较大影响，维修效果好的方法能够有效地减小检修总费用，而检测方法的影响相对较小。

[1] 代万宝, 宋春娜. 固定导管架式平台水下结构的定期检测[J]. 中国修船, 2008, 21(5): 49-51.

[2] 陈团海. 老龄平台结构完整性动态评估与风险控制[D]. 东营: 中国石油大学, 2011.

[3] Hellevik S G, Langen I, Sørensen J D. Cost Optimal Reliability Based Inspection and Replacement Planning of Piping Subjected to CO2Corrosion [J]. International Journal of Pressure Vessels and Piping, 1999(76): 527-538.

[4] 林红. 面向延寿工程的老龄平台寿命预测与管理研究[D]. 东营: 中国石油大学, 2008.

[5] Frangopol D M, Liu M, Multiob J. Optimization for Risk-based Maintenance and Life-Cycle Cost of Civil Infrastructure Systems[C].Proceedings of International Federation for Information Processing Digital Library, System Modeling and Optimization, Turin, 2005.

[6] 刘雅琴, 迟洪钦. 最优合并构成的有序遗传算法[J]. 上海师范大学学报(自然科学版), 2001, 30(4): 89-92.

Risk-based Inspection and Repair Planning for Ageing Platform

CHEN Tuan-hai1， CHEN Guo-ming2， ZHANG Chao1， ZENG Wen-yan3

(1. CNOOC Gas and Power Group, Beijing 100007, China; 2. Centre for Offshore Engineeringand Safety Technology, China University of Petroleum, Shandong Qingdao, 266580, China；3. China Classification Society Industrial Corporation Wuhan Branch, Wuhan 430022, China)

In order to determin the optimal inspection and repair scheme, the risk-based inspection and repair planning optimization model is presented. The calculation methods for the expected inspection, repair and failure costs in optimization model are proposed. The genetic algorithm in Matlab toolbox is employed to solve the optimization problem. Based on event tree analysis, the formula is derived to calculate inspection probability, repair probability and failure probability at the time of each inspection. Based on the optimization model, all the indeterminate factors of inspection intervals, inspection methods and repair methods are optimized. Finally, an ageing platform is considered in the optimization problem, and 10 candidate strategies are determined by combining different inspection methods and repair methods. The results shows that the risk of the platform will be decreased largely duo to inspection and repair optimization, and repair methods have a greater impact on inspection and repair planning than inspection methods.

ageing platform; risk; inspection and repair planning; optimization; genetic algorithm

2014-01-16

国家自然科学基金项目(No. 51079159): 超强台风下大型导管架平台动力灾变模拟及损伤控制。

陈团海(1984-)，男，工程师。

1001-4500(2014)03-0051-06

TE 952

A