基于折线滑动的岩质边坡非概率可靠性分析

王雨波 杨永生

(1.中钢集团马鞍山矿山研究院有限公司,安徽 马鞍山 243000；2.金属矿山安全与健康国家重点实验室，安徽 马鞍山 243000)

基于折线滑动的岩质边坡非概率可靠性分析

王雨波1,2杨永生1,2

(1.中钢集团马鞍山矿山研究院有限公司,安徽 马鞍山 243000；2.金属矿山安全与健康国家重点实验室，安徽 马鞍山 243000)

矿山高陡边坡稳定性研究是露天开采中的一个重要研究课题，由于边坡岩土体构成复杂，用传统的定值求解安全系数的方法已经不能很好地描述岩土体参数的不确定性。通过对折线滑动破坏模式的分区进行相关岩石室内试验，并根据实际工程岩体的情况对室内岩石参数进行强度折减，同时对边坡体不确定性参数进行区间描述。根据折线滑动的破坏模式，结合传递系数法，推导折线滑动非概率可靠度指标求解的功能函数，结合不同的区间解法对功能函数进行求解，得出最终的非概率可靠度指标，从非概率的角度对边坡可靠性进行研究分析。

边坡可靠性 非概率可靠性 折线滑动 区间理论

矿山高陡边坡稳定性研究是露天开采中的一个重要研究课题。传统的边坡稳定性分析方法是建立在确定性假设基础上，即认为边坡介质分布明确，各种作用因素明确，参数唯一。事实上由于边坡岩体组成或结构的不均匀性，导致安全系数Fs大于1的边坡未必稳定，又或是安全系数Fs小于1的边坡未必失稳这种“反常”的现象。实际上，由于岩土体介质是极其复杂的，无论是室内试验还是现场试验，试验数据都表现出不同程度的离散型。传统的概率可靠性分析方法从破坏概率的角度来评价边坡的稳定性，但是仍存在着以下不足：①试验数据有限的情况下需要确定概率分布形式；②假定的概率分布形式存在适用性问题；③概率分析模型对参数取值敏感性强，分布函数截尾数据的小误差可导致最后的可靠性指标不在可接受的范围，而在有限的取样和试验的条件下，往往难以避免这样的情况发生。基于区间理论的非概率可靠性分析用区间数对岩土体参数进行描述，能够较好地反映样本数据较少时参数取值的不确定性，减少了对数据信息量大的要求，在边坡工程研究中，确定某个力学参数的范围往往比确定其定值要容易得多，也比确定该参数的概率分布容易。本研究从非概率的角度出发，针对折线滑动的岩质边坡进行可靠性分析。

1 非概率可靠度理论

设

表示与结构有关的基本区间变量的集合，其中

xi∈Xi(i=1,2,…,n).

根据传统的概率可靠度分析方法可知，取

M=g(x)=g(x1,x2,…,xn),

(1)

为结构失效准则所确定的功能函数。当g(·)为xi(i=1,2,…，n)的连续函数时，M即为一区间变量，令

η=Mc/Mr,

(2)

式中，Mc为区间变量M的均值；Mr为区间变量M的离差。

由式(2)知，当η>1时，对∀xi∈Xi(i=1,2,…，n)，均有g(x)>0，结构安全可靠。当η<-1时，对∀xi∈Xi(i=1,2,…，n)，均有g(x)<0，结构必然失效。而当-1≤η≤1时，对xi∈Xi(i=1,2,…,n)，g(x)<0和g(x)>0均有可能。由于结构中所有的不确定参量在区间内取值的任意性，此时结构可能可靠，也可能不可靠。由式(2)可知，结构的安全程度随η值的增大而提高，因此，可用η作为边坡安全可靠程度的度量。

根据区间模型的非概率可靠度理论，对任意连续的极限状态函数M，基于区间模型的非概率可靠度指标定义为

(3)

满足条件

M=g(x1,x2,…,xn)=

G(δ1,δ2,…,δn)=0,

(4)

其中，

为与区间变量向量

对应的标准化区间变量向量，

可见，非概率可靠度指标η实质上就是‖·‖∞度量在区间变量标准化的扩展空间中从坐标原点到失效面的最短距离。

针对非概率可靠度指标的求解，目前常用的方法主要有定义法、组合法、截断法、转换法、优化法。

2 岩体参数区间描述

通过费辛柯法、格吉法以及经验折减法对试验强度参数进行折减，其中费辛柯法考虑了岩质边坡的高度以及裂隙的发育程度等因素，能较好地反应高陡边坡岩体内聚力情况，故计算内聚力最终取值采用费辛柯法折减，内摩擦角采用经验法折减，具体见表1。

表1 岩体计算参数最终取值

3 折线滑动功能函数的定义

定义边坡可靠度计算功能函数M=-Pi，即当下滑力Pi<0，则：①M=-Pi>0,此时边坡处于稳定状态，可靠度η>1；②当下滑力Pi=0，则M=-Pi=0,此时边坡处于极限平衡状态，可靠度η=1；③当下滑力Pi>0，则M=-Pi<0,此时边坡处于失稳状态，可靠度η<1。

由此可得边坡可靠性分析功能函数

M=-Pi=-Pi-1cos(αi-1-αi)-FsQicosαi+

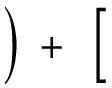
Wicosαi-Qisinαi-Uifi+cili=

-ψiPi-1-Fs(Qicosαi-Wisinαi)+

(Wicosαi-Qisinαi-Ui)fi+cili,

(5)

ψi=cos(αi-1-αi)-fisin(αi-1-αi),

式中，ψi为第i块滑体的剩余下滑力传递至第i+1块时的传递系数；Wi为第i块滑体的单块重力,kN/m ；αi为第i块滑体的滑面倾角,(°)；li为第i块滑体的滑面长度，m；ci为第i块滑体的滑面黏聚力，kPa；Fs为抗剪强度安全系数；fi为滑面上的摩擦系数；Qi为作用于分条上的水平总合力；Ui为滑面上的孔隙水压力合力，作用方向与滑面正交。

4 非概率可靠度指标求解及结论

(1)利用单纯形加速度法优化求解边坡的最危险滑动面。根据最危险滑动面对其可靠度指标进行计算，计算过程中考虑了震动和地下水的作用，根据最终坡面形状、地层产状以及地下水的情况，对滑动体进行条分，具体条分形式见图1。

图1 可靠度计算条分图(单位:m)

(2)运用区间数学理论求解岩质边坡折线滑动的功能函数，对优化的滑动面进行非概率可靠度计算，用自编程序进行迭代计算，具体的计算结果见表2。

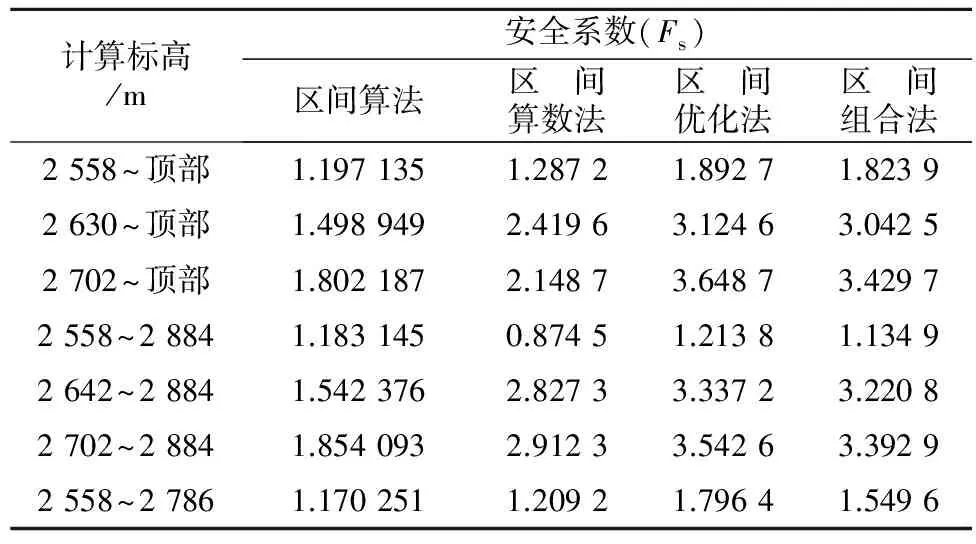
表2 计算剖面非概率可靠度计算结果

(3)通过区间算法针对具有折线滑动模式的岩质边坡进行了非概率可靠性分析，为边坡可靠性分析提供了新的思路。采用3种常见的区间算法进行计算，通过计算结果可以看出，不同计算标高下边坡的非概率可靠度指标均大于1，且危险滑面安全系数均大于1.15，可认定设计终了边坡是稳定的。

(4)在计算结果中可以看到，3种计算方法计算结果存在差异，其中2 558～2 884 m计算标高区间算数法的计算结果为0.874 5，根据区间非概率可靠度指标的定义，该段局部边坡是不稳定的。而优化法和组合法的计算结果分别为1.213 8、1.134 9，可以看出，区间算数法在评价边坡稳定性时存在较大差异。造成这种差异的原因主要是因为区间算数法在计算过程中的区间扩张所造成的，故运用区间算法进行可靠性分析时，需注意功能函数的区间扩张。应根据实际情况选择合理的区间算法，避免造成计算结果不能用于稳定性评价。

(5)从优化法和组合法计算的可靠度指标来看，二者计算结果存在差异，但结合二者的计算结果来看，本次可靠度指标是可靠的。

[1] 潘林锋,周昌玉.基于区间有限元法的压力容器可靠性分析[J].化工装备技术,2010,31(4):4-6. Pan Linfeng，Zhou Changyu.Reliability analysis of pressure vessel based on interval finite element method[J].Chemical Equipment Technology,2010,31(4):4-6.

[2] 邱志平,王晓军.不确定性结构力学问题的集合理论凸方法[M].北京:科学出版社,2008. Qiu Zhiping，Wang Xiaojun.Convex Method of Set Theory for the Uncertainty Structure Mechanical Problems[M].Beijing:Science Press,2008.

[3] 黄昌乾,丁恩保.边坡工程常用稳定分析方法[J].水电站设计,1999,15(1):53-58. Huang Changqian，Ding Enbao.The commonly used stability analysis method for slope engineering[J].Design of Hydropower Station,1999,15(1):53-58.

[4] 谭晓慧.边坡稳定可靠度分析方法的探讨[J].重庆大学学报：自然科学版,2001,24(6):40-44. Tan Xiaohui.The investigation of slope stability and reliability analysis methods[J].Journal of Chongqing University：Natural Science Edition,2001,24(6):40-44.

[5] 祝玉学.露天矿边坡设计的可靠性分析方法[J].水文地质,1980,47(5):42-46. Zhu Yuxue.The reliability analysis methods for slope design of open-pit[J].Hydrogeology,1980,47(5):42-46.

[6] 吕震宙,冯蕴雯.结构可靠性问题研究的若干进展[J].力学进展,2000,30(1):21-28. Lu Zhenzhou，Feng Yunwen.Some progress on study of structure reliability[J].Advances in Mechanics,2000,30(1):21-28.

[7] 魏宗平.机械非概率可靠性分析与可靠性优化设计研究[D].西安:西安电子科技大学,2006. Wei Zongping.Non-probability Reliability Analysis and the Study of Reliability Optimization Design for Mechine[D].Xi'an:Xidian University，2006.

[8] 武清玺.结构可靠性分析及随机有限元法:理论、方法、工程应用及程序设计[M].北京:机械工业出版社,2005. Wu Qingxi.Structure Reliability Analysis and Stochastic Finite Element Method:Theories，Methods，Engineering Application and Program Design[M].Beijing:Machine Industry Press,2005.

[9] 郭书祥,吕震宙.结构体系的非概率可靠性分析方法[J].计算力学学报,2002,19(3):332-335. Guo Shuxiang，Lu Zhenzhou.Non-probability reliability analysis methods of structure systems[J].Chinese Journal of Computational Mechanics,2002,19(3):332-335.

(责任编辑 石海林)

Non-probabilisticReliabilityAnalysisofRockSlopeBasedonPolygonalLineSliding

Wang Yubo1,2Yang Yongsheng1,2

(1.SinosteelMaanshanInstituteofMiningResearchCo.，Ltd.，Maanshan243000，China；2.StateKeyLaboratoryofSafetyandHealthforMetalMines，Maanshan243000，China)

Stability study of high-steep slope is an important research topic in surface mining.Because of the complex compose of the rock and soil mass，the uncertainty of the parameter of the rock and soil mass can not be precisely described by the traditional safety factor method.Through the rock laboratory test on the polygonal line sliding failure mode partition，strength reduction on the rock laboratory test parameter was made according to the actual situation of the rock mass in this slope engineering.At the same time，the uncertainty parameter of the rock and soil mass of the slope was described.According to the failure mode of polygonal line sliding，combing with the transfer coefficient method，the performance function for solving the non-probabilistic reliability index of the polygonal line sliding has been deduced.Combining with the different interval value，the solution of the function will be obtained，and the final non-probabilistic reliability index is got as well.From the perspective of the non-probability，the slope reliability analysis has been studied.

Slope stability，Non-probabilistic reliability，Polygonal line sliding，Interval theory

2014-09-26

王雨波(1987—)，男，助理工程师。

TD854.6

A

1001-1250(2014)-12-185-03