基于ARMA模型和趋势分析的铁谱定量参数分析与预测

曹海峰，韩念堔，宣征南

（1太原理工大学化学化工学院，山西 太原030024；2广东石油化工学院教务处，广东 茂名525000）

铁谱定量分析是铁谱技术的主要内容之一，是当前油液故障监测与诊断领域不可或缺的一部分。铁谱定量分析常运用于磨损趋势图的绘制，并通过划定的界限值和趋势曲线的走势分别对设备的磨损状态进行判定和预测。磨损趋势分析能够准确的对设备的磨损状态进行判定，但对设备磨损趋势的预测上却并不理想。ARMA模型是时序分析的一种，能够通过建立的时间序列达到对其未来数值的精确预测，因而被广泛的运用于多个行业，并被多名学者引入到油液监测与故障诊断领域［1－5］。油液的定量读数可以看作一个时间序列，理论上能够通过ARMA模型获取精确的预测值。然而，单个的定量读数并不能直接用于设备磨损状态的判定和预测，因此，很少有学者利用ARMA模型对铁谱定量读数进行分析预测。

本文结合铁谱定量趋势分析和AR模型各自的优点，提出了利用ARMA模型对定量参数进行预测，再利用趋势分析对观察值和预测值进行综合分析，达到对设备磨损状态进行精确判定和预测的方法。

1 ARMA（p，q）模型和趋势分析组合

1.1 ARMA（p，q）模型

ARMA（p，q）模型的全称是自回归移动平均模型，是由美国学者Box和英国统计学家Jenkins共同建立的时序理论。基本理念是：对于一个离散的时间序列｛Y1，Y2…Yn，…｝，其第n个观察值不仅与前n－1个观察值有关，还受系统自身的扰动影响，其数学表示方法如式（1）。

式中，p，q分别为该模型的自回归阶数与移动平均阶数。（Φ1，Φ2，…，Φp…）和（θ1，θ2…，θq，…）则分别是ARMA（p，q）模型的自回归系数和移动平均系数。｛et｝为与｛Yn｝独立同分布的白噪声序列。

当p＝0时，该模型为移动平均模型MA（q）如式（2）。

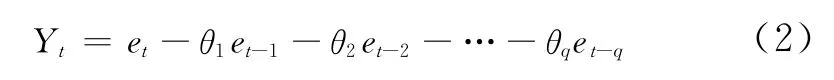
当q＝0时，该模型则被称为自回归模型AR（P）如式（3）。

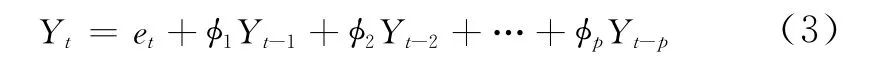
ARMA（p，q）模型只适用于平稳时间序列的描述，其具体的分析及预测过程主要包括数据预处理、参数识别、模型定阶及模型检验等步骤。

1.2 铁谱定量参数的趋势分析

铁谱定量参数的趋势分析主要是通过界限值的划定来对设备的磨损状态进行判定并利用趋势曲线的走势对设备的磨损进行简单预测。因此，定量参数分析的关键步骤在于找出设备运转过程中的“正常”、“注意”、“危险”、“警戒”状态的区间并划分正确的界限值。通常来说，学者们主要采用3δ法则来确立V1（基准值）、V2（警戒值）和V3（危险值）的值。

对于一组基于定量铁谱参数计算出的统计值样本X＝｛Xi｝（i＝1，…，n），由统计学知识可知，其样本均值和标准差分别为式（4），式（5）。

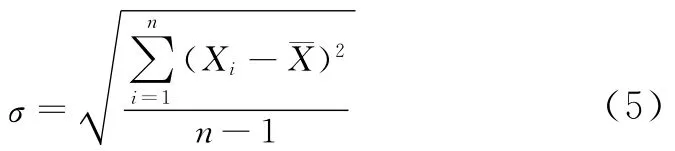
令

则

式中，i与n分别为样品的编号与数量。

通过V1、V2和V3的确定，整个趋势曲线就被划分成4块区域，而位于不同区域的样本值就代表着不同的磨损程度，进而反应出当时设备的磨损状态。

为了使划分的界限值能够更准确的对设备的磨损状态进行判定，闫辉等［6］将设备的故障率引入到界限值的划定因素中，何照荣等［7］也引入故障率理论并将传统的界限值公式进行了改进，如式（9）～式（11）。

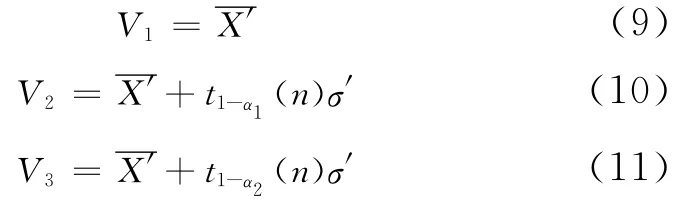
式中，α1，α1分别为“警戒状态”和“危险状态”的故障率，n则为样本的容量［7］。

1.3 ARMA（p，q）模型和趋势分析组合理论

对于已有的铁谱定量参数序列，建立时间序列并通过ARMA（p，q）模型对其进行分析预测，将获取的预测值与前期的观察值组合为新的序列并通过趋势分析的方法划定界限值，达到对设备磨损状态进行精确判定和预测的目的。

2 实验分析及验证

这里以实验室所搭建的实验平台中获取的铁谱定量数据进行前文理论的分析及验证。实验所用油样取自实验室自行搭建的实验平台，试验平台主体由YBP90L－4变频调速三相异步电动机、ZD10减速机和CZ2.5磁粉制动器构成，此外还有起冷却作用的水泵外联。其中电动机的额定功率为1.5kW，额定转速为1710r／min。减速箱为速比2的齿轮转速箱，所用润滑油为omala220齿轮液压油。按照美工石油协会（API）的分类方法，该润滑油能够满足齿轮传动时抗磨及防沉淀的要求。同时，实验过程、取样、数据获取均正确无误，能够正确代表设备的磨损状态。

因本次定量参数源于齿轮箱磨损实验的油样，磨粒粒度差异较大，故可直接选择DL（DL代表大于5μm磨损颗粒的光密度值）作为研究对象来判定及预测设备的磨损状态［7］。选取进入稳定磨损期之后的38个连续数据作为待研究的时间序列，其中，将前34个数据作为对DL趋势的分析预测样本，后4个则作为最终预测结果的验证。

利用SPSS软件作出本实验样本的序列图（见图1），可发现曲线并没有表现出季节性波动和明显的趋势变化，可初步认定为平稳序列。再作出其自相关及偏相关函数图（见图2、图3），可以看出样本的偏自相关系数仅在第一阶超出了2倍的标准差范围，其后的数值均在2倍的标准差之内，可作为零处理，因而，偏自相关系数1阶截尾；而由图3对样本自相关系数的描述可以看到，自相关系数表现出极强的趋近于零的趋势，因而可判断自相关系数拖尾。因此可以初步判定样本的拟合模型为AR（1）。

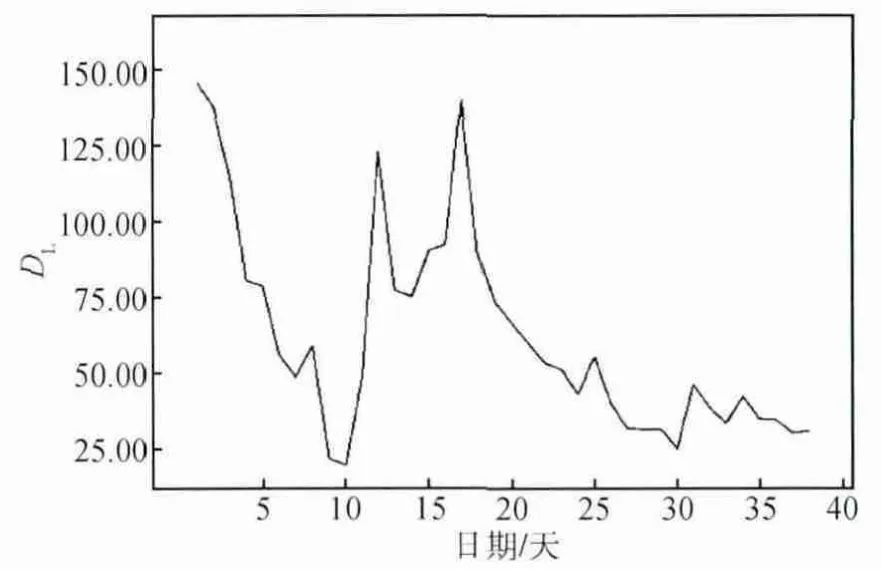
图1 DL序列图

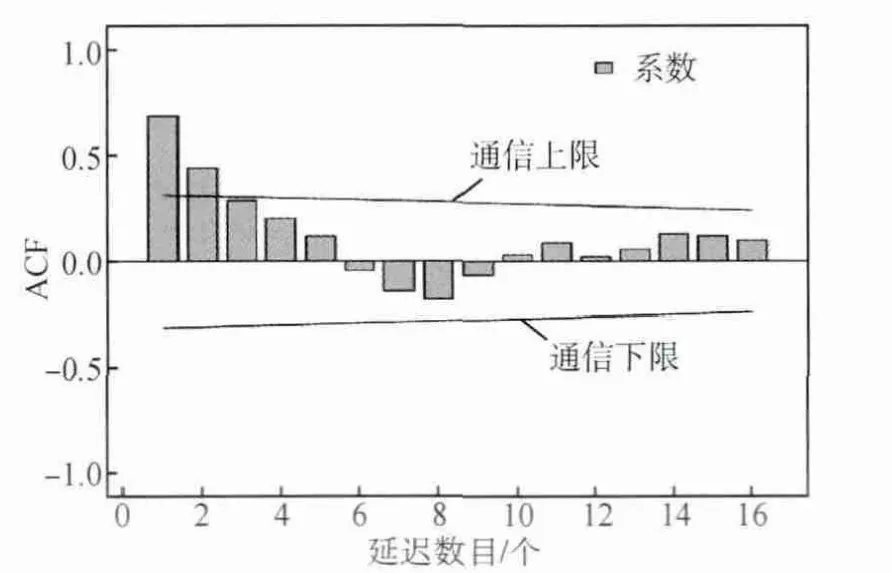
图2 自相关函数图

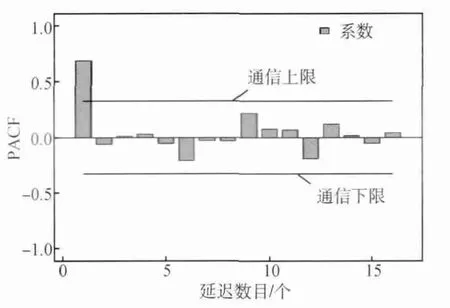
图3 偏相关函数图

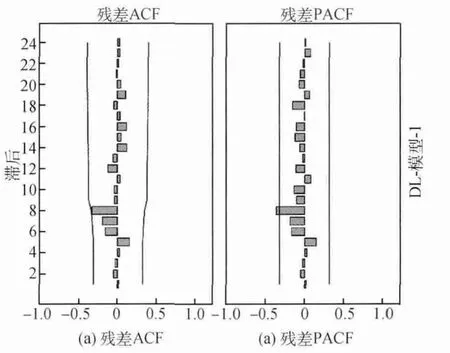
图4 残差的自相关及偏相关函数图

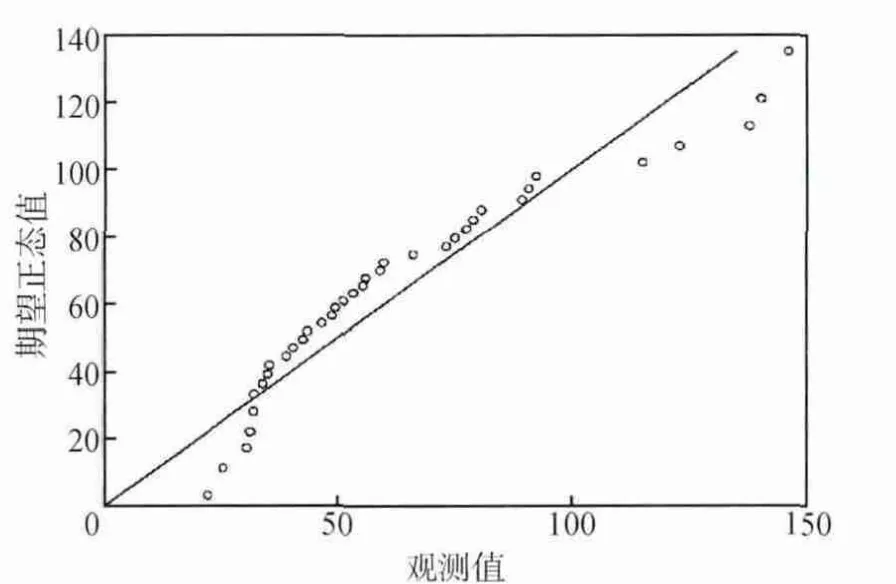
图5 DL真实值的Q－Q图

对AR（1）序列的残差进行拟合，通过它们的自相关函数和偏相关函数图（图4，图5）可以看出，残差的自相关函数和偏相关函数均在0阶和8阶截尾，故而，可认为残差为白噪声序列，即选取的模型是合理的。再对选定的AR（1）模型进行参数估计，并利用建立的模型对DL数值进行预测，可得到如表1所的预测值。

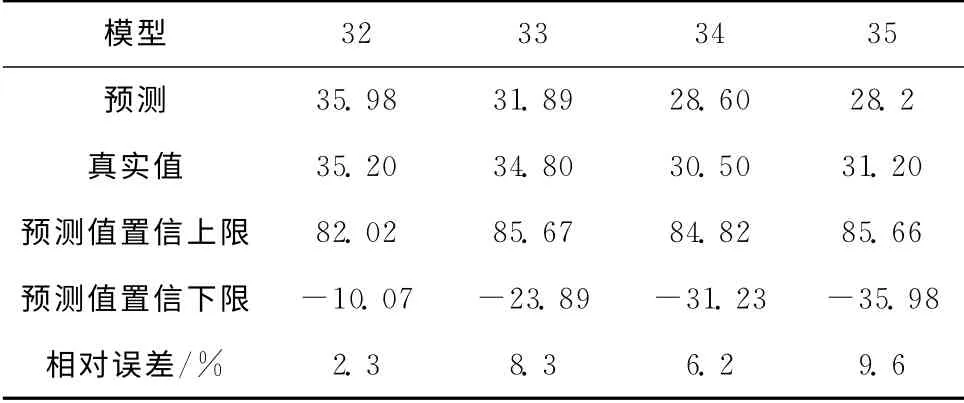
表1 DL预测值与真实值对照表

由表1所作的真实值与预测值之间的对比可以看出，其相对误差均在10%以内，说明预测精度较高，可以作为可信数据对设备在未来4天的磨损状态进行预测。将原始的34个真实值与4个预测进行组合作为一组新的序列，并与原始的真实值序列分别进行正态性检验，如图6，通过Q－Q值的观察对比，可发现其值基本上在第一象限的对角线附近徘徊，可认为其服从正态分布［8－9］。

利用1.2节 中 所 提 及 的 方 法 和 式（9）～式（11）分别对两组序列进行计算，最终可以得到如表2的界限值及图7的磨损趋势图。

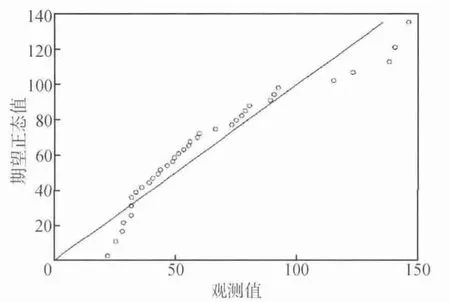
图6 DL真实值与预测值组合序列的Q－Q图

表2 两数据的界限值

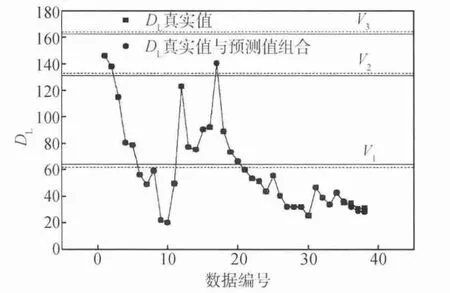
图7 两序列趋势分析图对照

图7中，虚线所示为DL真实值与预测值组合界限值划分的区间，而实线所示为DL真实值界限值划分的区间。通过对二者的比较可以看出，利用ARMA模型得出的DL预测值而做出的趋势图基本上与真实图像重合，界限区间也基本吻合，说明利用此方法对设备的磨损状态进行预测产生的误差极小，是一种值得信赖的预测方法。

3 结 论

（1）通过实例的验证，说明ARMA模型与趋势分析的组合方法对设备磨损状态进行预测的方法是可行的。且具有较高的精确度，对于预知设备磨损状态具有一定的参考价值。

（2）DL只是铁谱定量分析获取的诸多参数之一，因此，在实际的工作中，还可以根据需要选取最符合各自需求的参数来进行模拟预测。

（3）将趋势分析法和时序分析方法结合起来，实现优势互补就能够达到扬长补短的目的。在未来的故障监测与故障诊断的工作中，也可以引入其他的统计学理论方法，利用其优势来补充当前的方法理论，更好的为设备监测及故障诊断服务。

（4）为进一步提高ARMA模型的预测精度，还可以采用逐个预测的方法，并将前一个位置的预测值用真实值替换，这样就可以提升预测数值的精确度，进而确保对设备磨损状态预测的可靠性。

［1］ 李爱，陈果，候民利.航空发动机油样光谱分析的PSOLSSVM组合预测方法［J］.机械科学与技术，2013，32（1）：120－125.

［2］ 徐超，张培林，任国全，等.基于油液光谱LSSVR－AR模型的发动机故障预测［J］.内燃机学报，2010，28（2）：160－163.

［3］ 杨兴斌，冯辅周.发动机油液光谱分析预测模型研究［J］.振动与冲击，2010，29（s）：124－126.

［4］ 范庚，马登武.基于EMD和RVM－AR的航空发动机磨损故障预测模型［J］.计算机测量与控制，2013，21（7）：1746－1749.

［5］ 徐超，张培林，范红波，等.基于LS－SVM和AR模型的油液光谱数据预处理研究［J］.润滑与密封，2010，35（2）：59－63.

［6］ 闰辉，贺石中，毛宁，等.油液监测界限值传统计算方法的改进［J］.润滑与密封，2005（4）：81－83。

［7］ 何照荣，孙志伟，宣征南.基于铁谱定量分析的齿轮箱磨损分析［J］.机械传动，2013，37（7）：102－105.

［8］ 宗序平，姚玉兰.利用Q－Q图与P－P图快速检验数据的统计分布［J］.统计与决策，2010（20）：151－152.

［9］ 汪政红，周清志.两种多元正态性检验方法的应用和比较［J］.中南民族大学学报：自然科学版，2009，28（3）：99－103.