压水堆核电机组火用成本分析的矩阵算法
李永华,蒲亮,周思远
(1. 电站设备状态检测与控制教育部重点实验室(华北电力大学),河北省保定市 071003;2.国核工程有限公司,上海市 200233)
压水堆核电机组火用成本分析的矩阵算法
李永华1,蒲亮1,周思远2
(1. 电站设备状态检测与控制教育部重点实验室(华北电力大学),河北省保定市 071003;2.国核工程有限公司,上海市 200233)
为进行复杂能量系统的热经济学分析和评价,找出提高核电机组热经济性的新途径,基于火用经济学理论和矩阵算法,建立了压水堆核电机组热力系统火用成本分析通用模型。以某900 MW压水堆核电机组热力系统为例,进行了39股火用流的单位火用成本计算及分析,并对具体设备提出了明确的优化改进措施。结果表明:沿热力循环方向,各股火用流的单位火用成本先增加后减小;凝汽器输出火用流的单位火用成本最高,为7.1754,其次是凝结水泵和1号低压加热器,分别为5.249和4.1911。矩阵算法较常规火用成本分析法具有构造简单、矩阵元素填写法则简便、物理意义明确和规律性强等优点;利用矩阵算法的易编程性,便于开发出相应的计算及分析软件,进而为核电机组热力系统优化及故障诊断奠定理论基础。
核电机组;压水堆;热力系统;单位火用成本;矩阵方程
0 引 言
核电作为缓解能源紧张和减排温室气体的重要手段,具有广泛的发展前景[1]。随着我国核电机组装机容量的增加,核燃料(不可再生资源)消耗巨大,且乏燃料处理难度大、成本高,对环境危害大。在保证核安全的基础下,提高核电机组的热经济性对节约核燃料和降低发电成本具有重要的现实意义。
先进的能量系统分析方法为评价热功转换过程的完善性及提高核电厂的热经济性提供新的途径。Dunbar[2-4]基于热力学第二定律的火用分析法对运行中的核电厂进行了详细的火用分析,得出火用损失最大设备为反应堆,其次为汽轮机,并给出了具体的改进措施。Sayyaadi[5]应用热力学和火用经济学理论对典型的1 000 MW级压水堆核电机组进行了优化分析研究,对比分析3个不同层次的优化方法,最终得出火用经济学多目标优化为最佳优化方案。火用经济学理论的发展,使传统热力学分析得到进一步完善,Valero[6-10]等多位学者已将此理论应用于火电机组的成本分析、系统优化及故障诊断,但国内对核电机组进行火用成本分析的研究成果尚不多见。
我国核电发展路线以压水堆技术为主,压水堆核电机组与火电机组热力系统有着明显的不同,主要表现为核电站以核反应堆替代火电站的锅炉提供热能,汽轮机主要工作在湿蒸汽区,高压缸排汽进入再热器之前需要进行汽水分离等。因此,火电机组的火用成本分析方法很难应用于现行的核电机组,且常规方法求取能流的单位火用成本时需要对每个研究对象列出火用成本平衡方程,不易编制通用计算程序,变工况或在线计算工作量大。
为此,本文针对压水堆核电机组热力系统的特点,基于火用经济学理论和矩阵算法,研究适用于压水堆核电机组的火用成本分析模型,推导热力系统火用成本分布的通用矩阵方程,通过实例计算验证矩阵方程的正确性,分析热力系统单位火用成本的分布规律,并对具体设备提出明确的优化改进措施。
1 火用成本分析模型
1.1 物理模型
根据常规火电机组热力系统划分原则,结合压水堆核电机组热力系统的特点,将其划分为6个局部热力子系统:回热子系统、原子锅炉子系统、汽轮发电机子系统、汽水分离再热器子系统、给水泵子系统、凝汽器及凝结水泵子系统,如图1所示。本文中各种辅助汽水的分类可参考文献[11],主要参数含义如下:e为比火用 ;D为流量;W为功率;k*为单位火用成本,下标表示流的属性和位置。

图1 压水堆核电机组热力系统
1.2 数学模型
在划分好子系统的基础上,根据质量平衡方程和火用成本平衡方程,推导出局部热力子系统的火用成本分析方程。原子锅炉子系统、汽水分离再热器子系统的方程具体推导过程如下。
(1)原子锅炉子系统火用成本分析的通用物理模型见图2。根据质量平衡和火用成本平衡,建立原子锅炉子系统火用成本平衡方程,见下式。
(1)
(2)
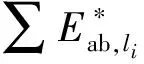
(3)
(4)
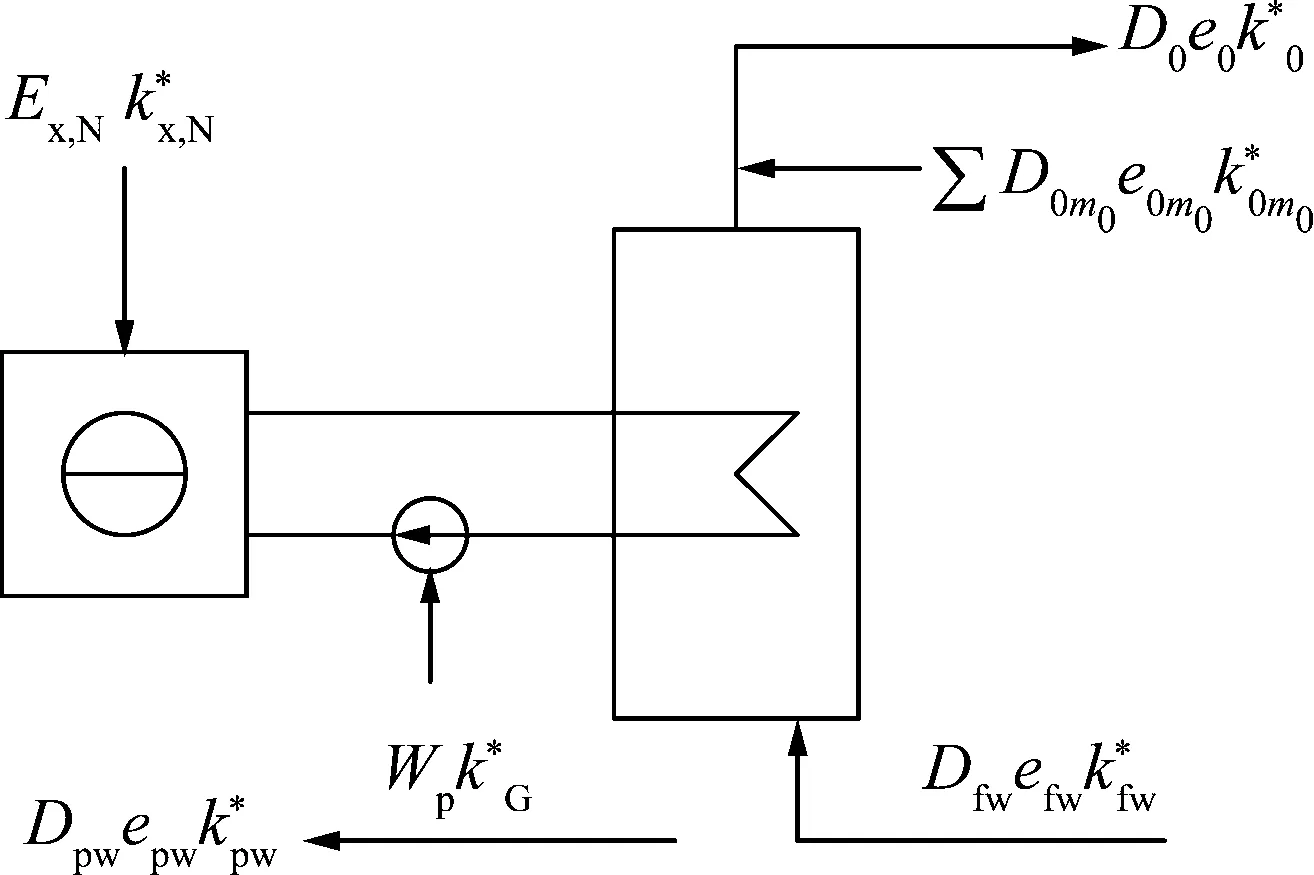
图2 原子锅炉子系统火用成本分析通用物理模型
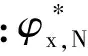
(2)汽水分离再热器子系统火用成本分析的通用物理模型见图3。根据质量平衡和火用成本平衡,建立汽水分离再热器子系统火用成本平衡方程,见下式。
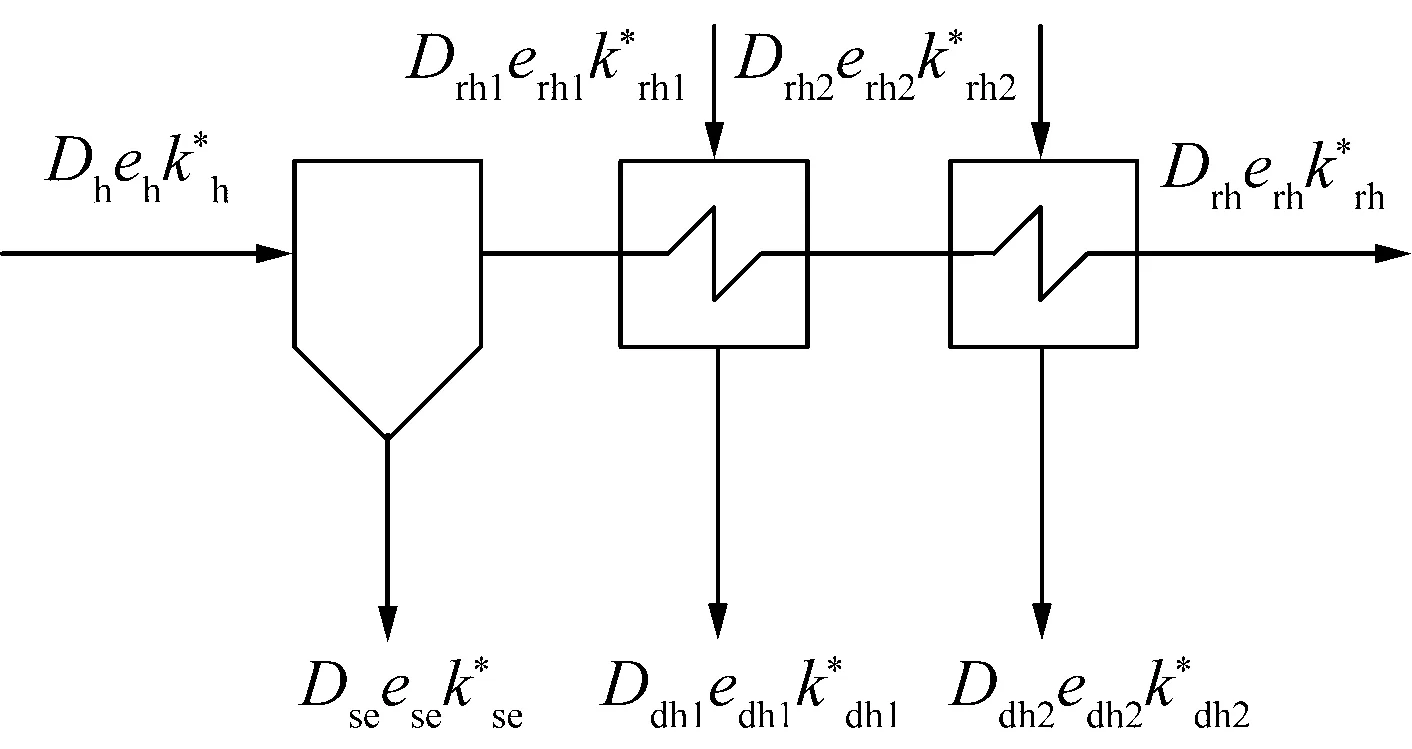
图3 汽水分离再热器子系统火用成本分析通用物理模型
(5)
(6)
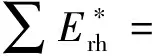
(7)
(8)
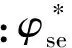
回热子系统、汽轮发电机子系统、给水泵子系统和凝结水及凝结水泵子系统与常规火电机组热力子系统类似,故方程推导及符号说明详见参考文献[12],这里不再赘述。
将各子系统的火用成本分析方程归并到一个统一的矩阵中去,得到整个热力系统的火用成本分析矩阵方程
(9)
式中:

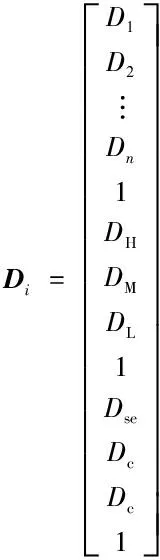
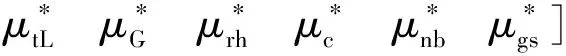
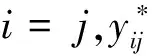
D1、D2……Dn为各级回热加热器抽汽流量;DH、DM、DL为汽轮机高、中、低压缸的进汽流量;Dc为低压缸排入凝汽器的蒸汽流量。
∑Diki为进出第i级加热器的第一类辅助蒸汽流量和,i取1,2…n;∑DtlH、∑DtlM、∑DtlL为进出汽轮机高、中、低压缸的辅助蒸汽流量和,如轴封漏气等;∑Dc,kj为进入凝汽器的第一类辅助汽水流量和。
Dw1、Dw2…Dwn为各级回热加热器给水(凝结水)流量;Dgs为给水泵中的给水流量。
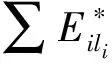
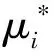
2 算例分析
2.1 机组简介
本文以某900 MW级压水堆核电机组为研究对象,图4为其原则性热力系统图,该机组由1个双流道高压缸和3个双流道、双排汽低压缸组成,回热系统为“两高、四低、一除氧”。反应堆额定热功率为2 895 MW,汽轮发电机组额定输出功率为983.8 MW,其他参数见文献[13]。
2.2 补充方程的建立原则
(1)从外部输入系统火用流的单位火用成本均规定为1。(2)子系统的非产品性输出火用的单位火用成本与输入火用的单位火用成本相等,所有产品火用流的单位火用成本相等。(3)若子系统的“燃料”为双线流,则构成双线流的2股火用流的单位火用成本相等[14]。
2.3 单位火用成本计算及分析
在热经济学分析中,将系统中的火用流赋予能量意义上的价值——火用成本,即获得该股火用流所需要消耗的外部火用,生产单位火用流所需要消耗的外部火用称为单位火用成本。该热力系统有39股火用流(如图4上火用流编号为1~39),这就需要计算39个单位火用成本。根据式(1)~(4)可以求解15个不同的单位火用成本,因此矩阵方程需要补充24个单位火用成本相等的关系式进行简化。由补充方程的建立原则可得,外部输入系统的核能火用的单位火用成本为1;第2、3、4、5、6、7、8、29、30、35、36、37股火用流的单位火用成本相等;第9、10、11、12、13、14、15、31、32、33、34股火用流的单位火用成本相等;第18、38、39股火用流的单位火用成本相等。综上所述,可得24个单位火用成本相等的关系式使矩阵方程封闭,有唯一解。通过Matlab软件编程计算,结果见表1。

图4 某900 MW压水堆核电机组原则性热力系统火用流图
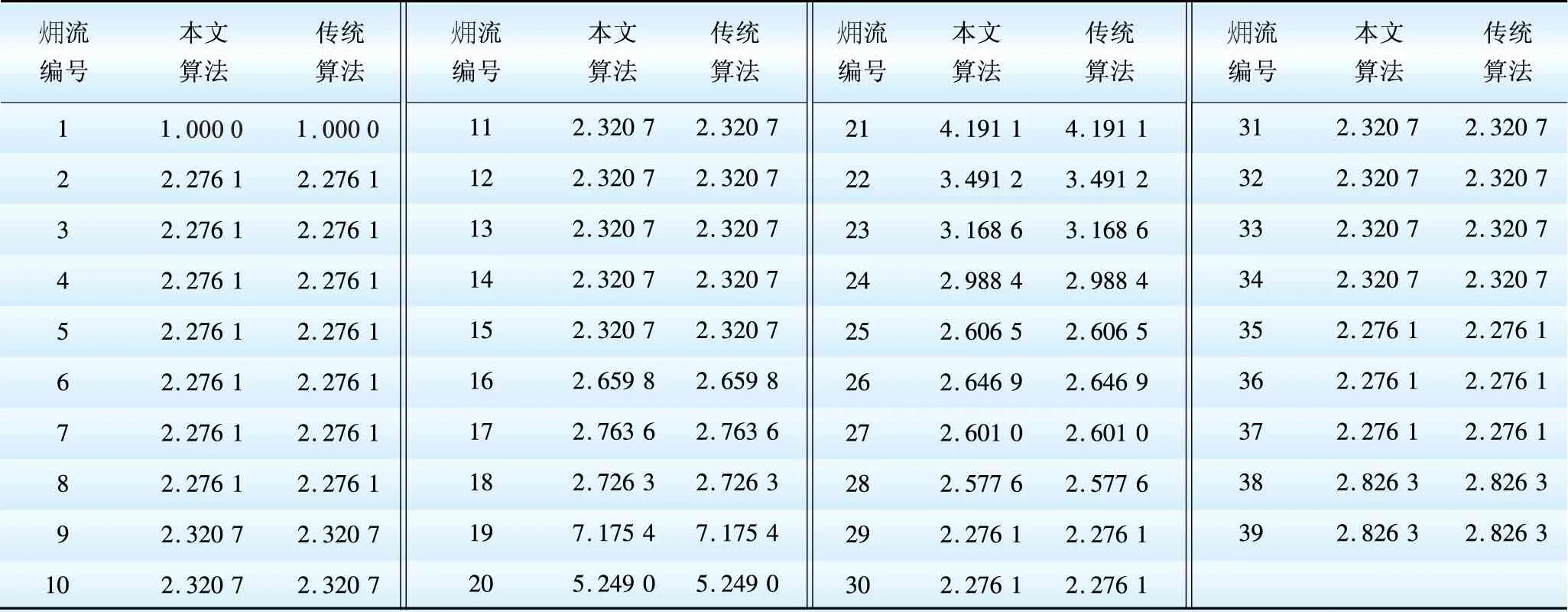
表1 某900 MW压水堆核电机组单位火用成本计算结果
由表1可看出:
(1)本文所述方法与传统算法(符号模式热经济学)计算的结果完全一致,验证了矩阵方程的正确性和准确性。
(2)沿热力循环方向,各股火用流的单位火用成本先增加后减小。靠近热力系统前端的单位火用成本较低,如主蒸汽(火用流编号为2)和主给水(火用流编号为28)的单位火用成本分别为2.2761、2.5776;远离热力系统前端的单位火用成本较大,如凝汽器热阱出口凝结水(火用流编号为19)的单位火用成本为7.1754。给水回热系统中,单位火用成本从低加到高加逐级减小,其中1号低加出口凝结水(火用流编号为21)的单位火用成本最大,为4.1911;7号高加出口给水(火用流编号为28)的单位火用成本最小,为2.5776。
(3)输出火用流的单位火用成本较高的设备有凝汽器、凝结水泵和1号低压加热器,相比其他设备,若减少相同的火用损,其节能潜力更大。因此,应设法减少凝汽器和1号低加内不可逆性引起的火用损失,如采取及时清理凝汽器和1号低加内的污垢,排除不凝结气体,确保1号低加疏水畅通等措施[15]。
(4)发电机输出电能(火用流编号为18)的单位火用成本为2.826 3,若引入核燃料的价格,可计算出发电机输出电能火用的热经济学成本,再考虑设备折旧、维修及劳务工资等非能量费用,可得出发电的实时成本,进而为上网电价的制定提供参考。
3 结 论
(1)基于火用经济学理论和矩阵算法,推导出压水堆核电机组热力系统的火用成本分布矩阵方程。该矩阵方程填写简单,各项物理意义明确,通用性强,且矩阵算法的易编程性使得单位火用成本的计算更加清晰和简便。
(2)应用该方程将全面揭示核电机组热力系统中各股能流的单位火用成本的分布规律,进而得出局部火用损对系统整体能量消耗的影响,为节能潜力挖掘指明了方向。
(3)在计算出单位火用成本的基础上,引入核燃料的价格及非能量费用,可对核电机组热力系统进行进一步的热经济学分析。从而为确定合理的发电成本提供依据,为核电机组热力系统优化及故障诊断奠定理论基础。
[1]祁恩兰.我国核电的建设形势及思考[J].电力建设,2009,30(5):1-4.
[2]Dunbar W R, Moody S D, Lior N. Energy analysis of an operating boiling-water-reactor nuclear power station [J]. Energy conversion and management, 1995, 36(3): 149-159.
[3]Durmayaz A, Yavuz H. Energy analysis of a pressurized-water reactor nuclear-power plant [J]. Applied Energy, 2001, 69(1): 39-57.
[4]崔雨.基于火用分析的900 MW级PWR核电机组热经济性研究[D].北京:华北电力大学,2011.
[5]Sayyaadi H, Sabzaligol T. Energoeconomic optimization of a 1000 MW light water reactor power generation system[J]. International Journal of Energy Research,2009,33(4):378-395.
[6]Valero A, Lozano M A, Bartolomé J L. On-line monitoring of power-plant performance, using exergetic cost techniques[J]. Applied thermal engineering, 1996, 16(12): 933-948.
[7]张超.复杂能量系统的热经济学分析与优化[D].武汉:华中科技大学,2006.
[8]程伟良,王清照,王加璇.300 MW 凝汽机组的热经济学成本诊断[J].中国电机工程学报,2005,25(8):126-129.
[9]Zhang C, Wang Y, Zheng C, et al. Energy cost analysis of a coal fired power plant based on structural theory of thermoeconomics[J]. Energy Conversion and Management, 2006,47(7):817-843.
[10]肖卫杰.结构理论研究及在热力系统故障诊断中的应用[D].北京:华北电力大学,2002.
[11]闫顺林,张春发,李永华,等.火电机组热力系统汽水分布通用矩阵方程[J].中国电机工程学报,2000,20(8):69-73.
[12]李永华,刘伟庭.火电机组热力系统火用成本分布通用矩阵方程[J].动力工程学报,2012,32(3):243-248.
[13]广东核电培训中心.900 MW 压水堆核电站系统与设备[M].北京:原子能出版社,2005:319-372.
[14]王加璇,张恒良.动力工程热经济学[M].北京:水利水电出版社,1995:82-83.
[15]廖军林,党小建.220 MW机组低压加热器疏水不畅分析及改造[J].电力建设,2012,33(11):46-48.
(编辑:蒋毅恒)
MatrixAlgorithmofExergyCostAnalysisonPWRNuclearPowerUnits
LI Yonghua1, PU Liang1, ZHOU Siyuan2
(1. Key Laboratory of Ministry of Education of Condition Monitoring and Control for Power Plant Equipment, North China Electric Power University, Baoding 071003, Hebei Province, China;2. State Nuclear Power Engineering Company, Shanghai 200233, China)
In order to implement thermoeconomics analysis and evaluation for complex energy system and find new ways to improve the thermal economy of nuclear power unit, a general model of exergy cost analysis on thermal system of pressurized water reactor (PWR)nuclear power units was established based on exergoeconomics theory and matrix algorithm. Taking the thermal system of a 900 MW PWR nuclear power unit as an example, the unit exergy cost of 39 exergy flows were calculated and analyzed, and explicit optimization improvements were proposed for the specific equipment. The results show that the unit exergy cost of each exergy flow increases firstly and then decreases along the direction of thermodynamic cycle; the maximum unit exergy cost is that of condenser output exergy flow, which is 7.1754, and followed by that of condensate pump and 1 low pressure heater, 5.249 and 4.1911 respectively. Compared with the traditional exergy cost analysis, the matrix algorithm has advantages in simple structure, convenient filling for each element of matrix, explicit physical meanings and obvious regularity. According to the programmability of matrix algorithm, a corresponding calculation and analysis software can be conveniently developed, which can provide a theoretical basis for the thermal system optimization and fault diagnosis of nuclear power units.
nuclear power units; pressurized water reactor; thermal system; unit exergy cost; matrix equation
TK 123
: A
: 1000-7229(2014)06-0137-05
10.3969/j.issn.1000-7229.2014.06.026
2013-12-16
:2014-02-21
李永华(1961),女,学士,教授,主要从事火电机组节能理论及节能技术方面的研究;
蒲亮(1989),男,硕士研究生,研究方向为电站设备状态监测、控制与信息技术,E-mail:ncepupuliang@163.com;
周思远(1987),男,硕士,助理工程师,研究方向为电厂运行经济性。

