向量函数的不变伪线性及其应用*

杨 杰， 黄龙光

(集美大学 理学院，福建 厦门 361021)

伪线性在最优化理论中有着重要作用，近年来，Lalitha[1]将伪线性概念推广到不可微函数，并给出这些函数的若干性质.Ansari[2]引入了非空凸集中的η-伪线性，但这些函数是不可微的，由此引发了将η-伪线性延伸到凸集和不可微函数中的想法；最近Ansari[3]又引入不变h-伪线性，研究了不可微且不变的伪线性函数的有关问题.

1 预备知识

设0表示Rn中的零向量，称映射f=(f1，f2，…，fm)：Rn→Rm是正齐次的当且仅当x∈Rn，r>0，有f(rx)=rf(x)；次奇的当且仅当x∈Rn{0}，f(x)=-f(-x).

定义1 映射f：Rn→Rm，

(a) 点x∈Rn沿着d∈Rn方向的Dini上方向导数定义为fD(x，d)=(fD1，fD2，…，fDm)，其中

(b) 点x∈Rn沿着d∈Rn方向的Dini下方向导数定义为fD(x；d)=(f1D，f2D，…，fmD)，其中

对∀d∈Rn有

fD(x；d)=-fD(x；-d)；fD(x；d)=-fD(x；-d)

(1)

由定义1可知，∀d∈Rn有

fD(x；d)≥fD(x；d)

(2)

由式(1)(2)，对∀x，d∈Rn有

fD(x；d)≥fD(x；d)=-fD(x；-d)

(3)

即fD(x；d)是次奇的.易知对每个确定的x∈Rn，fD(x；d)和fD(x；d)是正齐次的.

下面的条件C在研究伪线性中有重要作用.

条件C设K⊆Rn关于η是内凸的[3]，对∀x，y∈K，t∈[0，1]，有

(a) η(x，x+t(η(y，x)))=-tη(y，x)；

(b) η(y，x+t(η(y，x)))=(1-t)η(y，x).

显然，映射η(y，x)=y-x满足条件C.若η满足条件C，那么

η(x+t(η(y，x))，x)=tη(y，x)，t∈[0，1]

(4)

定义2 设K⊆Rn关于η是内凸的，且η满足条件C，f：K→Rm是η拟凸的当且仅当对∀x，y∈K，t∈[0，1]有

f(x+tη(y，x))≤max{f(x)，f(y)}

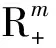
定义3 设K⊆Rn关于η是内凸的，h：K×Rn→Rm，称映射f：K→Rm，

(a) 关于η是h-伪内凸的当且仅当对∀x，y∈K，x≠y，有

等价地

(b) 关于η是h-伪内凹的当且仅当对∀x，y∈K，x≠y，有

等价地

(c) 关于η是不变h-伪线性的当且仅当关于η既是h-伪内凸的又是h-伪内凹的[3].

以下总设η满足条件C，K⊆Rn关于η是内凸的， f：K→Rm，h：K×Rn→Rm.

2 向量不变伪线性函数的若干性质

定理1 设对每个固定的x∈K，h(x；·)是线性的， f关于η是不变h-伪线性的且使得

fD(x；·)≤h(x；·)≤fD(x；·)

(5)

成立.那么对于任意x，y∈K，h(x；η(y，x))=0当且仅当f(x)=f(y).

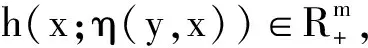
(6)

(7)

由式(6)(7)知h(x；η(y，x))=0，即f(x)=f(y).

充分性.对∀t∈(0，1)，

f(x+tη(y，x))=f(x)

(8)

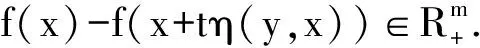
由f关于η是h-伪内凹的可知

(9)

根据条件C，

(10)

定理2 设对固定的x∈K，h(x；·)是线性的且f满足式(5)，那么f关于η是不变h-伪线性的当且仅当存在一个实值函数p：K×K→R，使得对所有的x，y∈K，p(x，y)>0且

f(y)=f(x)+p(x，y)h(x；η(y，x))

(11)

证明充分性.设f关于η是不变h-伪线性的，构造函数p：K×K→R，使p(x，y)>0(∀x，y∈K)，且

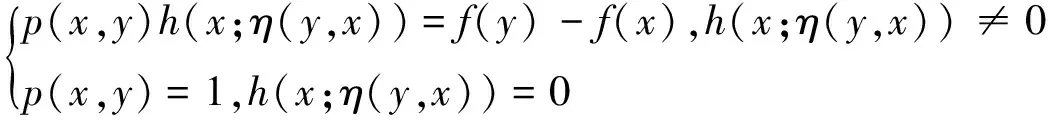
(12)

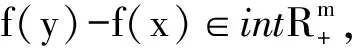
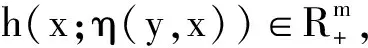
3 向量不变伪线性函数的优化问题

考虑下列优化问题

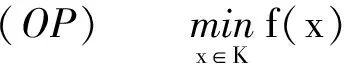
其中K⊆Rn关于η是内凸的，并设(OP)的解集S=argminx∈Kf(x)是非空的.

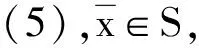
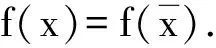
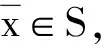
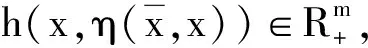
(13)

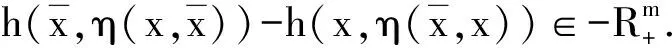
参考文献：

[1] LALITHA C S， METHA M. A Note on Pseudolinearity in Terms of Bifunctions [J]. Asia-Pac Oper Res， 2007(24)：1-9

[2] ANSARI Q H， SCHAIBLE S， Yao J C. Y-pseudolinearity [J]. Riv Math Sci Econ Soc， 1999(22)：31-39

[3] ANSARI Q H， REZAEI M. Invariant Pseudolinearity with Applications [J]. Optim Theory Appl， 2012(153)：587-601

[4] 胡毓达. 多目标规划有效性理论 [M].上海：上海科学技术出版社，1994