采用光学成像法的航空稳定平台振动幅度检测

王书民,张爱武,胡少兴,孟宪刚,段乙好,孙卫东

(1.首都师范大学三维信息获取与应用教育部重点实验室,100048,北京; 2.中国地震局地震预测研究所,100036,北京; 3.北京航空航天大学机械及自动化学院,100083,北京; 4.清华大学电子工程系,100084,北京)

采用光学成像法的航空稳定平台振动幅度检测

王书民1,2,张爱武1,胡少兴3,孟宪刚1,段乙好1,孙卫东4

(1.首都师范大学三维信息获取与应用教育部重点实验室,100048,北京; 2.中国地震局地震预测研究所,100036,北京; 3.北京航空航天大学机械及自动化学院,100083,北京; 4.清华大学电子工程系,100084,北京)

针对专用航空稳定平台振动检测设备成本高、难以在高光谱成像系统平台上集成应用等问题,提出了采用光学成像法的平台振动检测方法。将面阵CCD传感器与线阵高光谱传感器呈刚性紧密安装在航空稳定平台上进行影像数据的获取,并对获取的影像序列进行简化SIFT特征提取和分层金字塔实施的光流特征跟踪。考虑到振动对光谱成像等的影响,将振动分解在沿飞行方向和垂直于飞行方向2个方向上,并根据帧间相对运动模型解算出相对运动向量,然后由单次简谐振动造成的帧间特征不匹配,推导振动过程中振幅解算模型,并根据帧间运动矢量进行振幅的解算。实验结果表明,基于光学成像法进行振动检测可以达到微米级精度,满足系统集成应用需求,且其成本仅为多普勒振动测量方法的十几分之一。

光学成像法;航空稳定平台;振动幅度;检测;高光谱成像

航空稳定平台振动幅度的检测结果可以给机载高光谱影像直接地理定位误差的定性与定量分析[1]、光谱混叠研究[2-3]等提供重要依据。常见的平台振动检测方法有干涉计量法[4]以及虚拟仪器技术法[5]等,这些方法虽然测量精度高,但是需要专用的振动检测设备,成本高,不易与整个艇载平台系统进行集成应用,因此基于光学成像进行振动检测的方法已受到国内外学者的关注。关柏青通过分析不同形式运动造成的模糊图像,进行运动估计和振动测量[6];史红健等采用高速摄像机获取振动影像,并对影像进行时空域分析实现振动平台的测量[7];Li Qian等采用光学成像的方法先对图像进行傅里叶变化,并根据图像在频率域相位的变化,进行振动幅度的测量[8]。然而,上述方法均是通过非接触方式实现传感器对静止振动平台振动幅度的估计,不能完成对在轨运动平台振动幅度的实时测量。文献[9-10]采用小面阵CCD传感器结合SIFT特征与RANSAC算法,进行了卫星在轨颤动检测的可行性研究,解算出在轨卫星平台振动的幅度,但是SIFT特征检测与匹配耗时较长,不能进行振动幅度的实时估算与输出等。针对上述问题,本文采用光学成像法(Optical Imaging Method,OIM)进行振动幅度估计,如图1所示,先对序列影像进行简化SIFT特征提取与光流特征跟踪,计算帧间相对运动量,然后根据振幅计算模型进行振幅估算,实现振动幅度的实时计算与输出,最后将光学成像法与多普勒测量方法(Doppler Measurements Method,DMM)进行比较。实验结果表明,光学成像法的测量精度可满足系统要求,为艇载设备的集成、系统的减振性能设计以及影像数据的处理提供重要参考。

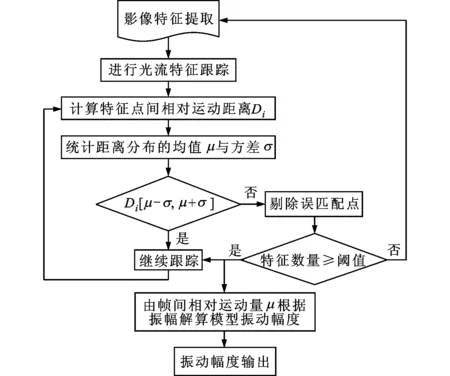
图1 基于OIM方法的振动幅度计算

1 特征提取与实时跟踪

1.1 SSIFT特征提取

Lowe提出尺度不变特征匹配(Scale Invariant Feature Transform,SIFT)[11],被广泛应用于图像特征提取与匹配。然而,SIFT特征提取耗时间长,实时性较差,难以实现特征的实时提取与匹配,因此本文对SIFT特征进行简化处理[12],在保证其鲁棒性的前提下,进一步提高特征提取的效率。

由于SIFT特征提取算法中特征描述子的生成占用整个算法80%以上时间开销,影像空间极值检测完毕后,对SIFT特征提取算法做如下简化:

(1)以极值点中心采用圆形窗体来确定统计的邻域范围,窗口采用David Lowe推荐的9σ×9σ(σ为尺度坐标),圆形窗口直径为9σ,在窗体内统计12个梯度方向;

(2)为保证光照不变性,将12个方向的梯度进行归一化,假设E=(e1,e2,…,e12)是特征点的特征向量,归一化后得到

(1)

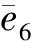
(2)

1.2 光流特征跟踪与匹配

基于梯度光流的角点跟踪方法实时性强,而且跟踪精度较高,如LK(Lucas-Kanade)算法[13]。假定t时刻图像上点x(x,y)处的灰度值为I(x,y,t),在t+Δt时刻,点x(x,y)运动到新位置(x+Δx,y+Δy),同时假定以x为中心的较小窗口w,在经过图像空间变换后t+Δt时刻x灰度值保持不变,即

I(x,t)=I(δ(x),t+Δt)

(3)

式中:δ(x)表示图像空间变换。当给定影像序列中的相邻两帧图像和某个窗口w后,确定影像空间变换参数即完成跟踪。但是,该算法过多地依赖特征窗口w的大小、物体的运动速度及图像目标的纹理等信息,当窗口w较小时,对于图像运动变换较大的情况,其空间变换参数估计精度有限;当窗口过大时,与假设情况不符。

通过构建影像金字塔实现角点梯度光流估计进行特征角点的亚像素跟踪[14-15],可有效解算上述跟踪问题。其基本思想是构建影像序列的金字塔,原始影像位于金字塔的底层,通过对原始影像进行下采样操作来产生金字塔中较高层影像,当影像分层到一定数量后,相邻帧间运动估计量变得足够小,即满足光流计算的约束条件。

由于在特征提取与跟踪的过程中会不可避免地引入错误目标,即跟踪错误,例如运动的汽车等,因此必须进行不稳定特征的剔除。经典的SIFT的特征匹配采用RANSAC算法进行特征匹配,通常需要进行多次迭代,时间开销大,计算复杂度高,难以满足实时性要求。

本文采用高斯概率模型进行不稳定角点剔除。假定当前帧和参考帧对应角点运动距离为Di(i=1,2,…,n),n为角点特征个数,在理想条件下,所有角点运动距离近似相等,其距离统计分布应满足高斯正态分布模型。设角点运动距离均值为μ、方差为σ,按照正态分布规律,样本落在区间[μ-σ,μ+σ]、[μ-2σ,μ+2σ]及[μ-3σ,μ+3σ]的概率分别是68.3%、95.5%及99.7%。通过设定信任区间可以剔除跟踪的错误目标和不稳定的角点。

1.3SSIFT特征提取与跟踪算法实施流程与步骤

本文采用简化SSIFT特征提取与跟踪,即先进行特征角点提取再进行跟踪的方法,当跟踪特征数量小于设定阈值时,放弃跟踪,重新提取特征角点。方法的具体步骤如下:

(1)输入影像,并对影像进行SSIFT特征检测,依次进行特征极值确定和描述符生成;

(2)采用金字塔分层实施的Lucas-Kanade算法,进行特征跟踪,其层数设定为3,并指定其特征搜索窗口w大小;

(4)统计所有对应特征点之间的距离Di,并求其分布均值μ和方差σ;

(5)设定信任区间A=[μ-σ,μ+σ],对于不满足Di∈[μ-σ,μ+σ]的对应特征点,直接剔除,否则予以保留,继续下一帧特征的跟踪,跳转步骤(3);

(6)判断当前跟踪保留的特征点数量N是否大于设定阈值,如果是继续跟踪,否则跟踪结束,跳转步骤(2)。

2 帧间相对运动与振幅计算

飞艇在飞行过程中受到气流颠簸、动力系统高频振动等影响,使得相邻帧间存在平移、缩放、旋转等运动,构建相邻影像帧间运动模型是帧间相对运动估计的前提条件,本文采用影像刚体变换模型,同时鉴于振动对光谱成像的影响,将振动分解在x与y两个方向上,即

(4)

式中:(xn,yn)为第n张影像像素坐标;(xn-1,yn-1)为第n-1张影像像素坐标;θ为相邻影像之间的旋转角度;dx、dy为平移量;γ为缩放因子。为方便计算,将式(3)进一步简化为

(5)

式中:a、b表示旋转参数;c、d表示水平与竖直方向的平移量。

对于相邻帧间运动参数实际解算,通常是通过匹配的m(m>3)对SSIFT特征点,构建2m个超正定方程,通过最小二乘可以求取运动补偿参数矩阵[abcd]T,即

(6)

综上,用于振动检测的影像序列数据应满足以下要求:

(1)根据相机的严格检校参数进行影像透视畸变校正,同时保证对象传感器与目标对象的距离大于等于10倍焦距,进一步减少弱透视的影响;

(2)根据POS位置姿态信息将所获得的影响数据投影在同一个指定的摄影平面上,或是保持相机传感器能够严格地垂直指向地面;

(3)用于振动检测的序列图像获取传感器的曝光时间Δt愈小愈好,即理想状态下limΔt→0,在一个振动周期内的某一瞬时时刻点获取图像数据。

基于上述条件,理论上,某时刻曝光位置C到D所获取的相邻影像数据,根据其运动方程进行平移、旋转等变换后能够很好地匹配,但由于振动的存在,会造成同一地物在相邻两张影像的对应特征不能很好地匹配。由振动造成的特征错位如图2所示。

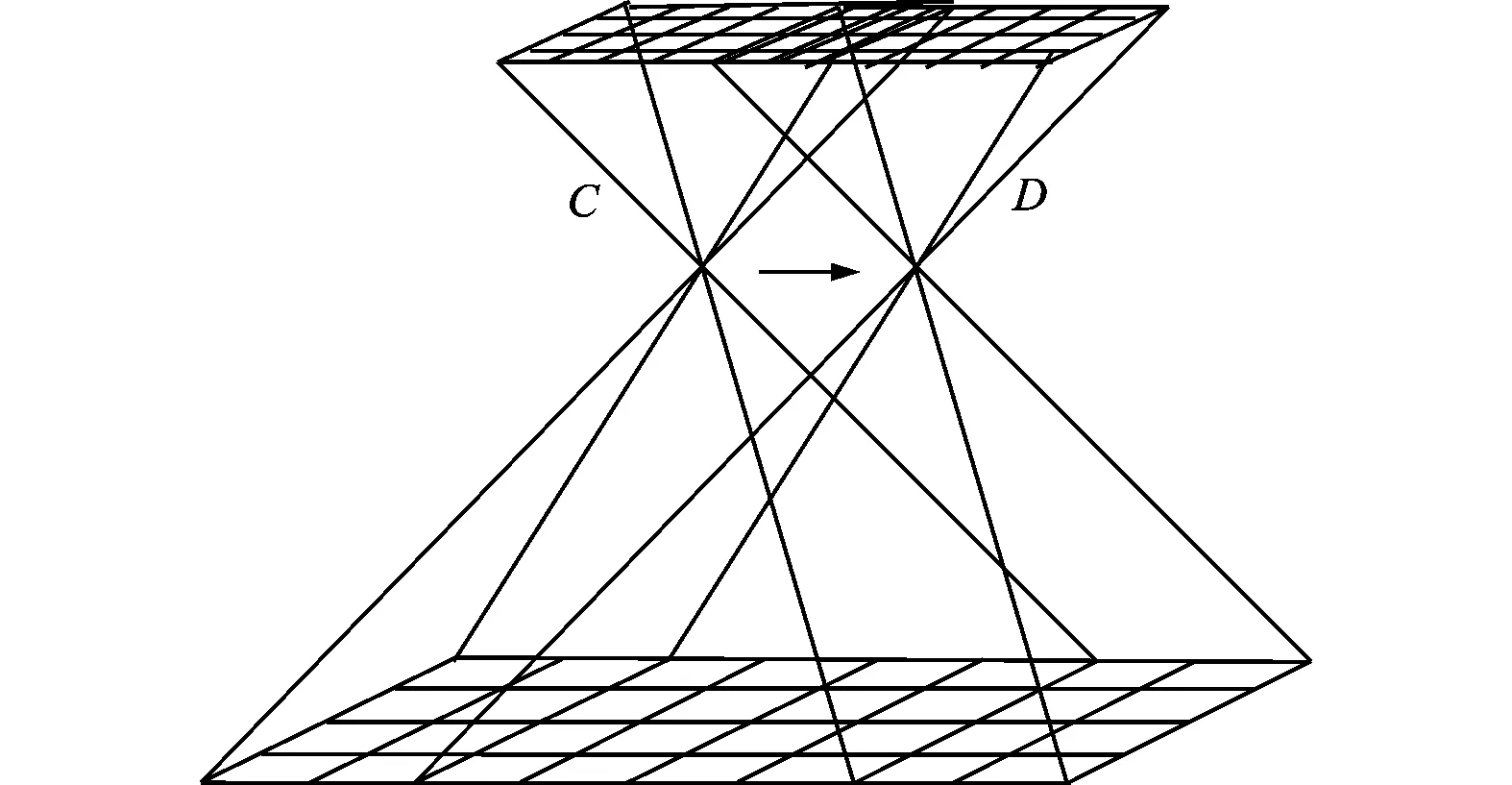
图2 振动造成的特征错位

为简化推导,假定平台一次振动过程为简谐振动,设艇载平台的振动幅度为A,第1次曝光时刻为t0,经过时间Δt,第2次曝光时刻为t0+Δt,由平台振动引起的像点运动为d;当t0与t0+Δt介于振动峰值两侧时,由于特征运动大小不能完全确定,因此采用平均法计算特征运动距离如下

d=(d′+d″)/2=A[sin(2πt0/T)+sin(2π(t0+Δt)/T)]t0/2

(7)

式中:d为特征平均像移量;d′表示t0+Δt时刻的特征像移量;d″表示t0时刻的特征像移量。传感器曝光位于振幅两侧时,平台振动振幅估算如图3所示,则振动幅度计算如下

A=2d/[sin(2πt0/T)+sin(2π(t0+Δt)/T)]

(8)

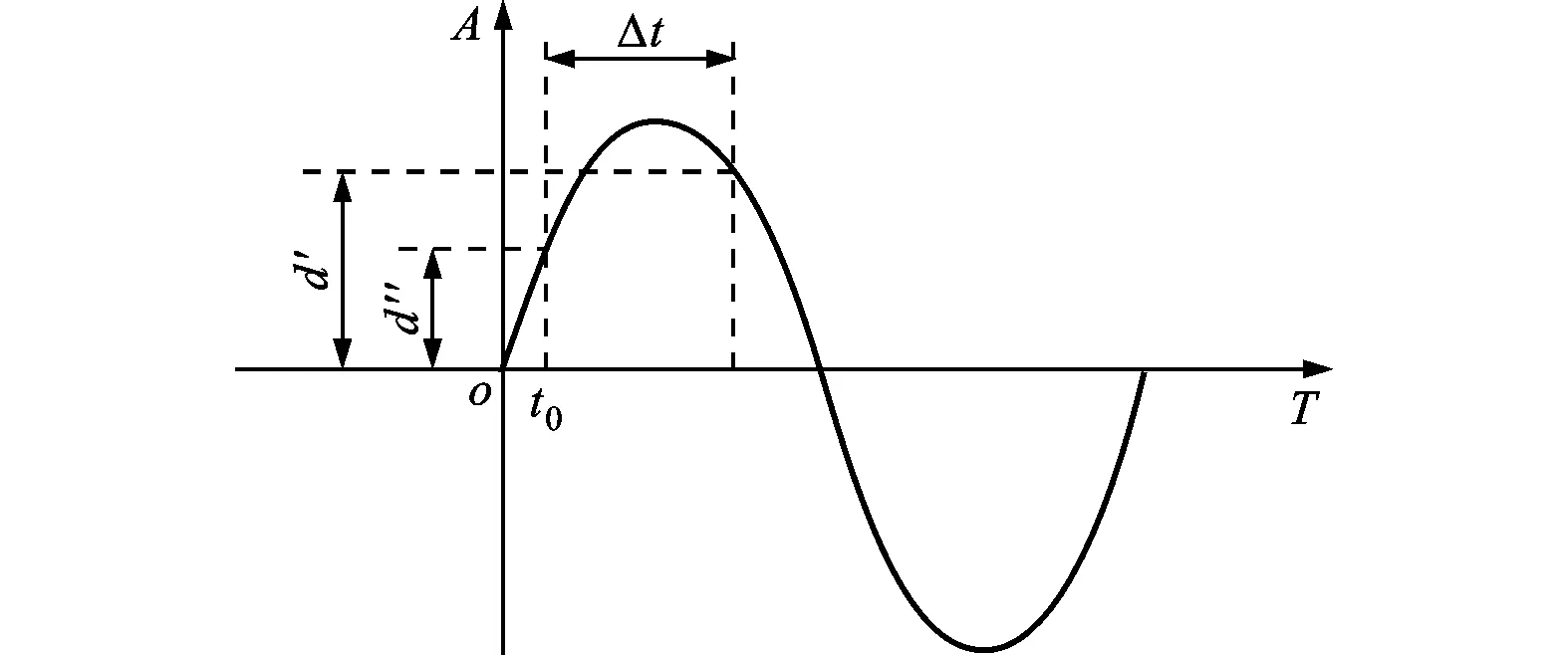
图3 传感器曝光位于振幅两侧时平台振动振幅估算

当t0与t0+Δt落在振幅A所处相位的一侧时,特征运动大小计算如下

d=d′+d″=A|[sin(2πt0/T)+sin(2π(t0+Δt)/T)]|

(9)

当传感器曝光位于振幅同侧时,平台振动振幅的估算如图4所示,则平台振动幅度计算如下

A=d/|[sin(2πt0/T)+sin(2π(t0+Δt)/T)]|

(10)

图4 传感器曝光位于振幅同侧时平台振动振幅估算

对于周期振动x(t)是多个简谐振动的合成,满足Dirichlet条件,极值个数有限,则x(t)可展开为傅里叶级数

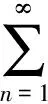
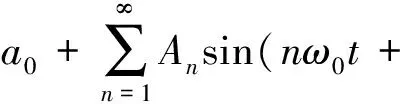
(11)

3 实验与分析

实验采用基于高空飞艇平台获取的影像序列数据,平台上主要搭载了线推扫式高光谱成像系统以及用于平台振动检测的影像序列获取传感器,在进行影像获取之前进行了传感器的严格检校,线阵传感器与面阵传感器呈刚性紧密安装在稳定平台上,传感器与动力系统安装示例如图5所示。实验采用佳能5d markⅡ作为振动检测的图像获取传感器,相机焦距为28 mm,获取的影像序列分辨率为640×480像素,单个像素大小为6.4 μm,获取速率为25帧/s,通过特征的提取与跟踪进行特征运动距离的计算。

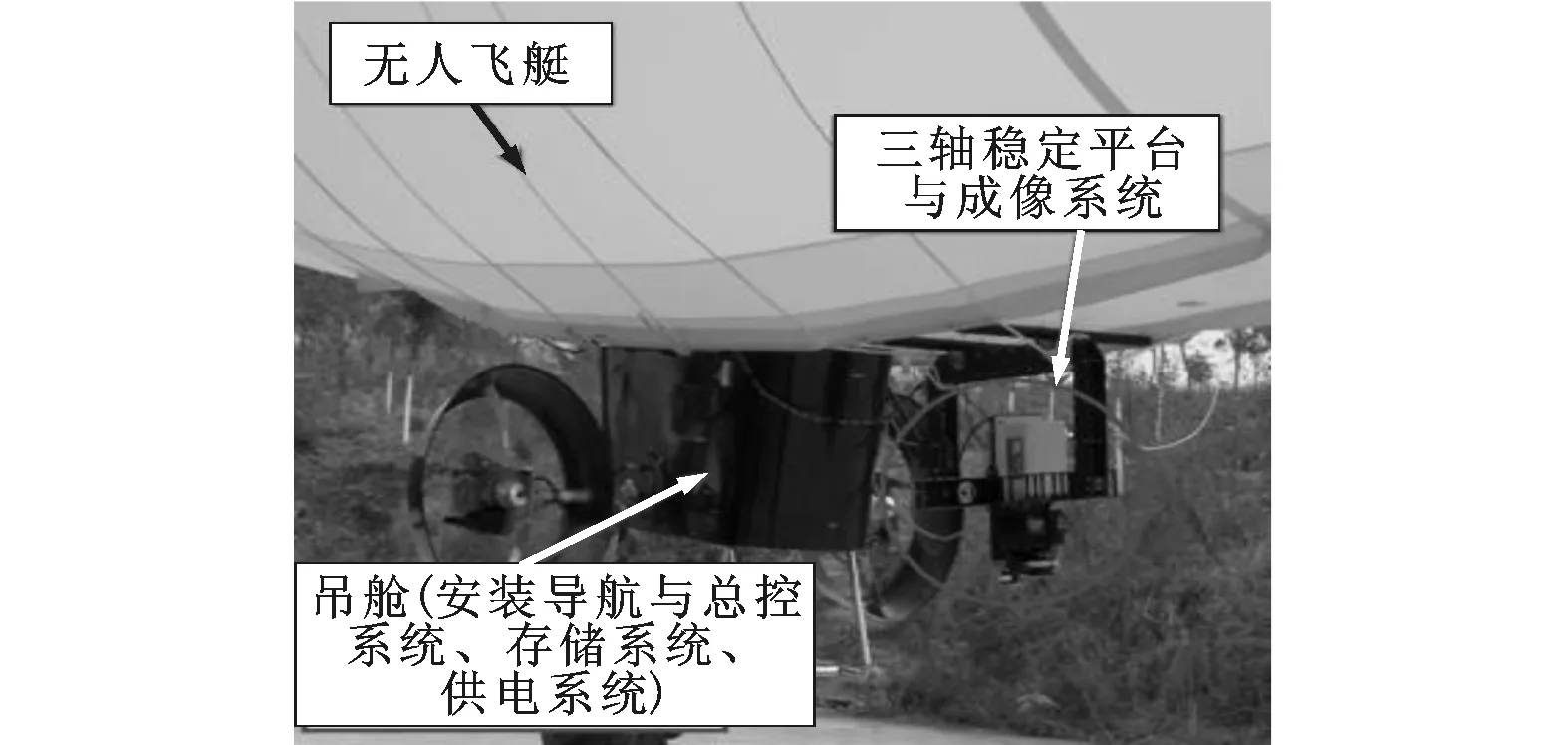
图5 传感器与动力系统安装图示

3.1 特征跟踪与相对运动估算

本文实验在惠普Hpxw4600台式计算机上进行,其主要配置为intel酷睿2处理器,主频3.06 GHz,内存4 GB,同时采用VC9.0软件为平台结合OpenCV库函数编写了影像特征跟踪与振幅解算程序,单帧影像处理平均耗时89.2 ms。

在SSIFT特征提取与跟踪过程中,由于汽车等运动目标光流特征变化明显,因此也可能作为特征角点进行跟踪,但是汽车等运动目标在相邻两帧之间存在运动,造成计算的帧间对应特征相对运动距离解算错误,必须予以剔除,如图6所示。

圆点为提取的特征角点;方框中行驶的汽车作为误匹配点被剔除(a)提取特征角点 (b)剔除运动目标

实验采用100帧影像通过帧间特征的跟踪匹配和运动模型解算,进行帧间相对运动的估计。同时,将帧间相对运动划分到沿飞行方向和垂直于飞行方向,即y与x方向,x方向的帧间相对运动解算结果如图7所示,y方向的帧间相对运动解算结果如图8所示。

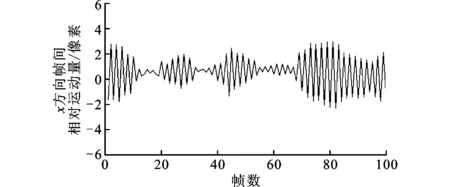
图7 x方向的帧间相对运动量

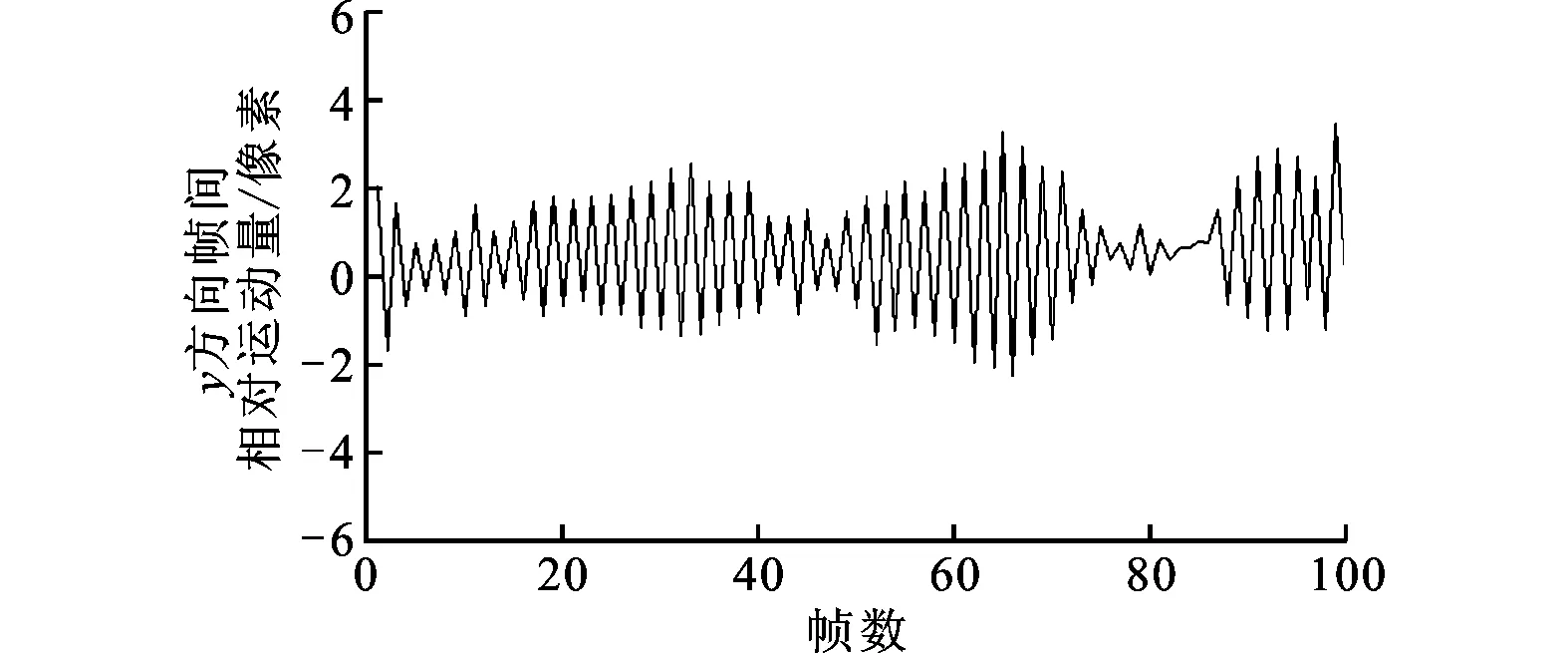
图8 y方向的帧间相对运动量

3.2 振动平台振幅计算

为简化计算,假设其第一帧影像的获取时间t0=0,飞艇动力系统采用4缸发动机,发动机每个冲程即每个工作循环曲轴转动2圈,每个工作循环各个缸按照固定顺序各点火爆炸一次,即每转爆炸2次转动2次。对于转速为6 000r/min的4缸发动机,其振动频率为6 000/60×2=200Hz。相邻两帧之间的曝光间隔te为1/25=0.04 s,根据上述假设与振动幅度计算公式,随机抽取10个时刻点的影像运动矢量,分别采用OIM方法与DMM方法解算出10组平台振动幅度数据,如表1所示。

表1 2种方法的平台振动幅度测量结果比较

实验结果表明:①基于光学成像方法进行平台振动检测是可行的,将极大减少平台振动估算的成本,缩短平台集成测试的周期;②x、y方向上的振动幅度是不同的,其对推扫成像的影响也是不同的;③平台振动的幅度不是固定的,随外部环境而变化;④在复杂的外部环境下,航空稳定平台的振动幅度可以达到140μm,因此在后期的影像直接定位处理中,应该根据振动幅度的大小，分别给予定位误差不同程度的补偿;⑤鉴于面阵CCD传感器与线推扫式高光谱相机呈刚性紧密安装在稳定平台上,因此振动对面阵CCD相机与线阵高光谱传感器的影响可视为一致,即可对两者施加相同频率与振幅的振动。

4 结论与展望

本文通过实验验证了基于光学成像方法进行振动检测的可行性,给出了艇载稳定平台的振动检测结果,为线推扫式高光谱成像系统集成、安装及减振设计等提供了重要参考。下一步将研究振动频率的测定,同时将根据检测出的平台振动幅度对光谱成像的影响进行仿真分析,对整个系统在集成安装过程中的减振设计提出明确要求;同时根据平台振动结果,对振动造成的影像定位误差进行补偿,将进一步提高线推扫式成像系统直接地理定位精度。

[1] 洪光烈,郭亮.线振动对合成孔径激光雷达成像的影响分析 [J].光学学报,2012,32(4): 262-268.

HONG Guanglie,GUO Liang.Analysis of effects of line vibration on imaging quality of synthetic aperture radar [J].Acta Optica Sinica,2012,32(4): 262-268.

[2] 王晓燕,唐义,唐秋艳,等.卫星平台振动对色散型光谱仪光谱成像质量的影响分析 [J].光谱学与光谱分析,2011,31(12): 3407-3411.

WANG Xiaoyan,TANG Yi,TANG Qiuyan,et al.Analysis of influence of satellite platform vibration on spectral imaging quality of dispersive imaging spectrometer [J].Spectroscopy and Spectral Analysis,2011,31(12): 3407-3411.

[3] TANG Qiuyan,TANG Yi,WANG Xiaoyan,et al.Synthetical imaging simulation of satellite vibration [J].Infrared and Laser Engineering,2012,41(3): 803-810.

[4] 杨翀.光学干涉计量用于振动测量的算法和实验研究 [D].合肥: 中国科学技术大学,2012.

[5] 刘彬彬.基于虚拟仪器技术的激光纳米振动测量方法研究 [D].哈尔滨: 哈尔滨工程大学,2007.

[6] 关柏青.基于主动序列模糊图像的运动估计和振动测量 [D].上海: 上海交通大学,2007.

[7] 史红健,朱飞鹏,何小元.基于时空域分析影像云纹的低频振动测量 [J].光学学报,2011,31(4): 1-5.

SHI Hongjian,ZHU Feipeng,HE Xiaoyuan.Low frequency vibration measurement based on spatiotemporal analysis of shadow moire [J].Acta Optical Sinica,2011,31(4): 1-5.

[8] LI Qian,WANG Shigang,GUAN Baiqing,et al.A machine vision method for the measurement of vibration amplitude [J].Measurement Science and Technology,2007,18(5): 1477-1486.

[9] 闫利,胡晓斌.卫星在轨颤动检测的可行性研究 [J].测绘通报,2013(7): 19-22.

YAN Li,HU Xiaobin.Feasibility research of on-orbit satellite vibration detection [J].Bulletin of Surveying and Mapping,2013(7): 19-22.

[10]胡晓斌,闫利.卫星颤动在轨检测可行性研究 [J].测绘地理信息,2013,38(4): 18-20.

HU Xiaobin,YAN Li.Research on feasibility of satellite on-orbit flutter [J].Journal of Geomatics,2013,38(4): 18-20.

[11]LOWE D G.Distinctive image features from scale-invariant keypoints [J].The International Journal of Computer Vision,2004,60(2): 91-110.

[12]刘力,彭复原,赵坤,等.采用简化SIFT算法实现图像快速匹配 [J].红外与激光工程,2008,37(1): 181-184.

LIU Li,PENG Fuyuan,ZHAO Kun,et al.Simplified SIFT algorithm for fast image matching [J].Infrared and Laser Engineering,2008,37(1): 181-184.

[13]LUCAS B D,KANADE T.An interactive image registration technique with an application to stereo vision [C]∥International Joint Conference on Artificial Intelligence.San Francisco,CA,USA: Morgan Kaufmam Publishers Inc.,1981: 674-679.

[14]陈白帆,蔡自兴.基于尺度空间理论的Harris角点检测 [J].中南大学学报: 自然科学版,2005,36(5): 751-754.

CHEN Baifan,CAI Zixing.Harris corner detection based on theory of scale-space [J].Journal of Central South University: Science and Technology,2005,36(5): 751-754.

[15]江志军,易华蓉.一种基于图像金字塔光流的特征跟踪方法 [J].武汉大学学报: 信息科学版,2007,32(8): 680-683.

JIANG Zhijun,YI Huarong.A image pyramid-based feature detection and tracking algorithm [J].Geoscience and Information Science of Wuhan University,2007,32(8): 680-683.

(编辑 刘杨)

VibrationAmplitudeDetectionofAeroStabilizationPlatformAdoptingtheOpticalImagingMethod

WANG Shumin1,2,ZHANG Aiwu2,HU Shaoxing3,MENG Xiangang1,DUAN Yihao1,SUN Weidong4

(1.Key Laboratory of 3D Information Acquisition and Application,Ministry of Education,Capital Normal University,Beijing 100048,China; 2.Institute of Earthquake Science,China Earthquake Administration,Beijing 100036,China;3.College of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing100083,China; 4.Department of Electronic Engineering,Tsinghua University,Beijing 100084,China)

A platform vibration detection algorithm for aero stabilization platform is proposed to solve the problem that the special vibration detection device is expensive and is hard to integrate and to apply in hyperspectral imaging systems.The algorithm is based on the optical imaging method,and accesses image data by adopting and installing frame CCD sensor on the airship-borne platform with line push-broom hyperspectral camera tightly.The simplified SIFT (Scale Invariant Feature Transform,SIFT) features are extracted from the image sequence,and pyramidal implementation of the Lucas Kanade feature tracker is employed to track features.The vibration is then decomposed on the fly direction and the direction that is perpendicular to the fly direction by considering effect of the vibration to spectral imaging.Then the relative motion vector between neighbor frames is solved using the image motion model.The unmatched features between the neighbor frames caused by the platform vibration is used to derive the vibration amplitude calculation model,and then the amplitude is calculated from the motion vector.Experimental results show that the vibration amplitude detection based on the optical imaging method reaches micron precision and satisfies the application requirement,while its cost is only one over ten of the cost of Doppler vibration measurement.

optical imaging method; aero stabilization platform; vibration amplitude; detection; hyperspectral imaging

2013-11-07。

王书民(1985—),男,博士,助理研究员;张爱武(通信作者),女,教授,博士生导师。

国家科技支撑计划资助项目(2012BAH31B01);国家自然科学基金资助项目(41071255);北京市自然科学基金重点资助项目(KZ201310028035)。

时间:2014-04-30

10.7652/xjtuxb201406005

TP732

:A

:0253-987X(2014)06-0025-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140430.1754.001.html