基于RBF神经网络的压水堆堆芯三维功率分布方法研究
夏 虹,李 彬,刘建新
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001;
2.深圳中广核工程设计有限公司,广东 深圳 518000)
各种堆芯功率监测方法中,中子通量密度监测较温度、压力等热工参数监测更能及时、直接反映堆芯功率的变化,而堆芯三维功率分布的实时监测对于反应堆的设计、安全及控制优化具有极其重要的意义。早期压水堆堆芯三维功率监测通过利用少数几个裂变探头在堆芯多个测量孔道中的移动测量一系列中子通量密度数据,经计算得到堆芯的三维功率分布,此探测方法呈现一次三维分布用时约90 min[1]。但在负荷跟踪等瞬态工况下不能实时呈现,且在小尺寸的实验堆和具有燃料球流动的球床气冷堆中,由于不能布置探测器孔道,无法通过堆内中子探测器来监测堆芯功率的三维分布。赵强[2]利用实际探测校正的方法计算堆芯的功率分布,在一定程度上减少了存储器的使用并提高了三维分布呈现的实时性,基本能实现核电厂稳态运行的在线仿真,但该方法在堆芯瞬态功率突变情况下的实时性尚有待进一步提升。李富等[3]对堆外探测器读数与堆内三维功率分布的关系进行了深入研究,发现堆外中子探测器的读数变化可反映堆芯的三维功率变化,且利用谐波法[4]能快速呈现堆芯功率的三维分布。李伟[5]则利用最小二乘法将堆芯三维功率分布和相应的堆外探测器计数拟合出响应矩阵,并利用求得的响应矩阵成功拟合出堆芯在稳定功率运行情形下的三维功率分布,但当功率水平发生变化时,拟合结果需考虑对控制棒末端所在节块的重构值进行适当修正。
针对以上对堆芯三维功率分布进行计算及监测时所遇到的问题,本文提出利用RBF神经网络对堆外核测量系统与堆芯功率三维分布间的非线性对应关系进行合理建模,实现对堆芯功率三维分布的实时监测,并在实验过程中通过几种方法提高模型的精度。
1 模型基本要素
1.1 堆外核测量系统
压水堆堆外中子探测系统由源量程、中间量程和功率量程组成,对变化范围为0.1~1×1011cm-2·s-1的中子通量密度进行监测。以300 MW压水堆核电厂为例,源量程使用含硼计数管探测器,测量启堆时的中子通量密度,这些探测器安装在装有初始启动源的堆芯两侧的平坦部分,约在堆芯高度1/4的位置;中间量程使用γ补偿电离室作为中子敏感元件并安装在相应的仪表孔道内,这些探测器被安置在相当于堆芯高度1/2的位置;功率量程用4个非补偿电离室(图1,A、B、C、D为非补偿电离室,每个分为上下两部分)探测泄漏出堆芯的中子通量密度。

图1 300 MW核电厂堆外核测量系统平面示意图
堆外中子探测系统在反应堆功率运行或负荷跟踪时,可实时呈现堆芯轴向一维功率分布。该一维功率分布包含大量的堆芯中子通量密度变化信息,这是用其呈现堆芯功率三维分布的基础。
1.2 RBF神经网络
RBF神经网络是一种由RBF神经元构成的3层前向神经网络,第1层为输入层,由信号源节点组成;第2层为隐藏层,其神经元模型的变换函数采用非线性径向基函数,该函数呈中心对称且向外衰减,具有局部响应的特点;第3层为输出层, 是对输入信号综合处理后的最终映射层。
RBF神经元结构模型及RBF神经网络的函数模型示于图2。
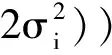

图2 RBF神经元结构模型(a)及RBF神经网络的函数模型(b)
RBF神经网络与其他前向神经网络相比,具有结构简单、训练简洁和学习收敛快的特点,能逼近任意非线性函数。同时通过训练对神经元间连接权值的调整,也具有信息的分布式存储、并行处理、自组织、自学习等神经网络的普遍功能。堆外核测数据与堆芯功率分布之间的复杂非线性对应关系,可通过RBF神经网络的合理设计得到恰当的模拟。
2 基于RBF神经网络的堆芯功率三维分布模型
2.1 RBF神经网络三维堆芯模型的设计

图3 模型构建过程示意图
为了利用RBF神经网络模拟出堆芯三维功率与堆外核测量数据的对应关系,需合理组织安排RBF神经元,使其生成具有特定功能的神经网络组合。模型的结构设计示于图3。首先,以一族神经元按某种连接方式,生成一多输入单输出神经网络,该神经网络经训练和权值调整,能模拟复杂的映射函数,其输出对应1个节块的功率值;其次,对堆芯的每层N个节块,使用N个相同结构的神经网络,这些神经网络的输入相同,输出则因各节块而异;最后,有序安排各层节块功率值即可得到堆芯三维功率分布。
2.2 RBF神经网络模型的训练
利用已知的历史数据对所设计的神经网络进行训练,以调整每个网络中神经元的连接权值。图4为用神经网络模拟堆芯功率分布示意图,中间部分为设计的神经网络,两边分别为已知数据输入和堆芯三维功率分布输出,训练过程中,神经网络自动调节每层神经元间的连接权值,使输出与输入对应。

图4 用神经网络模拟堆芯功率分布
在此,对历史数据的要求是:在若干组功率水平状态下,堆外核测量系统所呈现的轴向功率分布数据和对应的堆芯所有节块的功率数据同时采集。根据现有的实验条件,本次设计所使用的数据采自300 MW压水堆全范围仿真机,如表1所列,z(12×1)i表示1个功率状态下对应的轴向12点归一化功率分布数据,D(121×12)i表示相应功率水平的三维堆芯功率分布的1 452个数据。每组对应关系可让神经网络进行1次学习,经若干次训练,通过验证对比,待神经网络的输出达到了满意精度,即可用它拟合堆芯功率分布。

表1 仿真机采集数据类型
3 仿真实验和模型的验证
3.1 模型正确性的验证
用9组数据训练神经网络,再用训练好的神经网络结合1组轴向分布数据z(12×1)k,拟合堆芯分布d(121×12)k,与基准分布D(121×12)k进行比较,从拟合趋势和拟合误差两个角度进行评价,若不出现严重误差,则认为模型正确。实验观察了k=6时的情形,因数据量较大,为便于展示,在此只取1/4堆芯第10层的37个节块功率拟合值进行误差统计。统计结果显示:该层平均误差为7.788×10-3;最大误差为9.090×10-3;最小误差为7.212×10-3。
此外,用相同的方法对堆芯其他层进行了相同的实验,误差统计结果与文献[5]中使用拟合矩阵拟合堆芯功率变化状态下的结果一致,3个误差指标均在同一量级,且少数几个大误差也出现在控制棒末端节块。由此,通过实验初步证明了模型是正确的。
3.2 训练次数对模型精度影响的验证
根据神经网络的特性,加强训练可提高其对复杂函数的拟合精度。本次实验选取第6个功率组的D(121×12)6作为基准的验证对象,用z(12×1)6作为神经网络的拟合输入。分别对神经网络训练6次、7次、8次、9次后让神经网络执行堆芯功率拟合任务,对应得到拟合分布d6(121×12)6、d7(121×12)6、d8(121×12)6、d9(121×12)6。为便于展示,在此只取拟合数据di(121×12)6(i=6、7、8、9)与基准数据D(121×12)6的level 3作对比,误差比较列于表2。
从表2可看出,拟合最大误差随训练次数的增加而显著减小,由7.2%降到了1.42%;最小误差具有一定的随机性;平均误差由6组训练时的1%降到7组训练时的0.38%,且减小到千分量级后,呈现随机特性。对其他层进行同样的实验,也得到了类似的现象。本次实验结果表明,加强训练能提高模型的拟合精度。
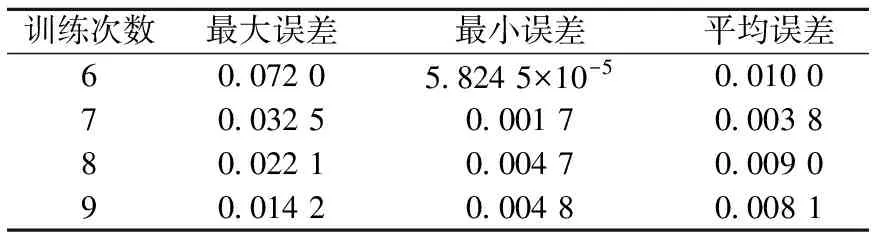
表2 训练次数不同情况下第6个功率点level 3节块拟合误差比较
3.3 神经网络输入节点对模型精度影响的验证

图5 轴向23点功率分布拟合示意图
为得到更多的轴向分布点,从而增大神经网络的输入节点,对仿真机上采集的轴向12点分布数据z(12×1)进行简单处理:在每两个数据间插入它们的平均值,即可插入11个值,从而形成轴向23点分布数据,即z(23×1),拟合方式如图5所示。另外将影响功率分布的T4、T3组控制棒棒位数据归一化后也引入到轴向功率分布点的阵列中,形成23+2点输入。3种输入情形下,均将拟合分布d(121×12)6与基准分布D(121×12)6进行比较,其他9组数据作训练。比较全体1 452个节块的最大、最小误差和平均误差。总体误差统计列于表3。
从表3可见,3种输入状态下神经网络模型对整体拟合的平均误差小于0.8%,且输入节点越多,平均误差越小,符合理论推测。实验中还发现,最大误差出现在控制棒末端的少数几个节块,误差大小和出现位置与文献[5]中通过拟合矩阵方法拟合得出的结论一致。最小误差则比拟合矩阵方法的拟合最小误差还小,说明轴向功率分布越精细,给出的轴向分布点越多,该神经网络模型的拟合越精确。另外,控制棒棒位参数加入到输入端并未对拟合结果起到显著改善效果,说明本设计的拟合不需考虑棒位参数。
为探究大误差形成的原因,实验引入了训练数据结构分析,通过对比分析大误差结块随功率变化时的热中子通量密度变化,得出以下结论:大误差的出现是由训练数据在拟合区段变化梯度过大、线性趋势不好导致的。

表3 3种输入情形的误差比较
3.4 训练数据结构对模型精度影响的验证
为验证上述实验关于大误差成因的结论,需找到一个控制棒末端所在节块的功率变化梯度较小、线性程度较好的功率点,对其进行拟合,并与之前的第6个功率组的实验结果作对比。
通过对仿真机采取的数据进行分析,选择第2个功率点作为拟合分布实验点,将D(121×12)2定为基准分布,将其他9组数据作为神经网络的训练组,得到拟合分布d(121×12)2,调整程序,运行出总体1 452个节块的平均误差为7.648 0×10-3,最大误差为3.801 0×10-2,最小误差为3.059 1×10-4。由此可见,本次实验相对于前面的实验结果,误差明显缩小,虽然在控制棒末端(第2个功率状态,T4控制棒末端在第3层)的节块仍出现了本次拟合的最大误差,但该误差水平可接受。这组实验充分说明了功率变化情况下,只要用于训练的数据功率间隔不是太大,即节块的功率变化梯度不大,功率变化的线性度就较好,神经网络的拟合结果可达到较理想的精度。
4 总结
本文利用RBF神经网络设计的堆芯三维功率分布智能监测方法能有效地将堆外中子计数与堆芯三维功率分布对应。实验结果表明,该方法不仅能有效减小控制棒末端的误差,而且通过增强训练、增加与神经网络输入对应的轴向功率分布测点、优选训练数据结构等方式能有效地提升模型的拟合精度。除此之外,在实验时,当用训练好的RBF神经网络拟合功率分布时,用普通双核计算机顺次计算每层37个节块功率值用时总共约0.2 s,若用高性能计算机并行运算每个节块的功率值,然后并行通信呈现三维功率分布,将大幅缩减计算时间,由此可见该模型具有非常优越的实时性,能满足控制系统实时性的要求。
参考文献:
[1] 刘国发. 核电站测量仪表与控制原理[M]. 深圳:大亚湾核电运营管理公司培训中心,2008:125-129.
[2] 赵强. 核电厂反应堆堆芯物理在线仿真系统研究[D]. 哈尔滨:哈尔滨工程大学,2006.
[3] 李富,周旭华,王登营,等. 采用堆芯外探测器监测堆内功率分布[J]. 核动力工程,2010,31(S2):92-96.
LI Fu, ZHOU Xuhua, WANG Dengying, et al. Monitoring of in-core power distribution by ex-core detectors[J]. Nuclear Power Engineering, 2010, 31(S2): 92-96(in Chinese).
[4] 罗征培,李富,王亚奇,等.在核反应堆安全运行中使用在线监视技术的设想[J]. 核科学与工程, 2000,20(1):32-38.
LUO Zhengpei, LI Fu, WANG Yaqi, et al. An idea about applying the online surveillance techniques to safe reactor operation[J]. Chin J Nucl Sci Eng, 2000, 20(1): 32-38(in Chinese).
[5] 李伟. 基于堆外计数的堆芯功率分布重构方法研究[D]. 哈尔滨:哈尔滨工程大学,2009.

