泡沫填充波纹夹芯梁的面内压缩破坏模式分析

韩宾,文灿,于渤,倪长也,秦科科,张钱城,卢天健,慈军,耿丽

(1.西安交通大学轻质结构和材料多学科研究中心, 710049, 西安; 2.西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安;3.广东顺德西安交通大学研究院, 528300, 广东佛山;4.东莞市永强汽车制造有限公司, 523407, 广东东莞)

泡沫填充波纹夹芯梁的面内压缩破坏模式分析

韩宾1,2,文灿1,2,于渤1,2,倪长也1,2,秦科科1,2,张钱城1,2,卢天健1,2,慈军3,耿丽4

(1.西安交通大学轻质结构和材料多学科研究中心, 710049, 西安; 2.西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安;3.广东顺德西安交通大学研究院, 528300, 广东佛山;4.东莞市永强汽车制造有限公司, 523407, 广东东莞)

为了提高波纹夹芯结构作为高铁车厢或油罐车罐体容器外壳在面内压缩载荷下的结构稳定性,提出了在波纹芯体空隙中填充聚酯泡沫的设想,理论研究了泡沫填充波纹夹芯梁的面内压缩破坏行为,同时对面内压缩破坏进行了数值有限元验证。泡沫填充波纹夹芯梁面内压缩下的主要破坏模式为宏观弹塑性屈曲、面板弹塑性起皱2种模式。结合宏观尺度上芯体的均匀化等效弹性常数,建立宏观屈曲破坏的理论模型;将泡沫等效为Winkler弹性基,建立面板起皱破坏的理论模型。对304不锈钢波纹夹芯板和Rohacell 51泡沫填充材料,构建结构的破坏模式图,有限元计算结果从破坏模式和临界载荷2个方面验证了理论预测的可靠性。在此基础上,对泡沫填充波纹夹芯结构进行质量最小优化设计,获得结构的最优化几何尺寸。综合考虑承载、能量吸收、减振、隔热等多功能特性,相较于空心波纹夹芯结构和金字塔点阵夹芯结构,泡沫填充波纹复合结构具有潜在的重要工程应用价值。

罐车;泡沫填充波纹夹芯梁;破坏模式;屈曲分析;结构优化

金属夹芯结构质量轻、刚度大,兼具抗冲击、减振、散热等多功能特性[1],在多个领域发挥着重要的作用。其中,如图1所示的波纹夹芯结构由于较低的制造成本,被广泛应用于建筑、包装、运输等行业,特别是被用作车辆、舰船、动力机械装备、高速列车、罐体容器及航空航天飞行器的外壳结构等,故研究波纹夹芯结构的综合力学行为对实际工程结构设计具有一定的指导意义。在实际工程应用中(如高铁列车厢体、油罐车罐体等),波纹夹芯结构的面内压缩性能是关键的力学性能指标,是确保结构轻量化和安全性的基础。

(a)空心及泡沫填充波纹夹芯试样照片

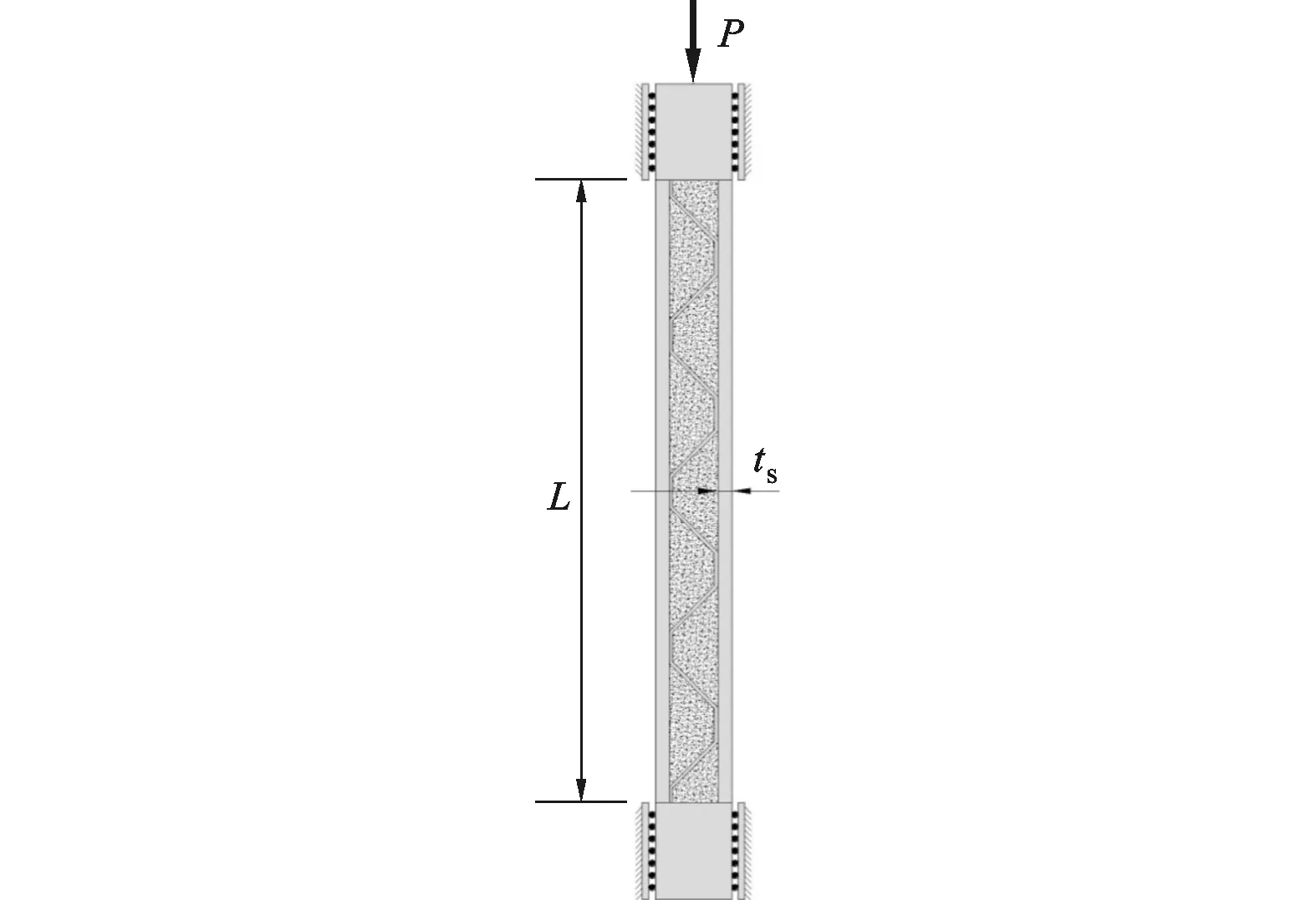
(b)泡沫填充波纹夹芯梁承受面内压缩示意图

目前,国内外仅有Biagi等从实验、理论和计算方面详细研究了铝合金及304不锈钢作为基体材料的波纹夹芯板的面内压缩力学行为[2-3]。若金属波纹夹芯板的基体材料为理想弹塑性,在面内压缩载荷作用下可能发生的破坏模式为弯曲失稳导致的整体弹性屈曲、面板弹性起皱/屈服、芯体剪切失稳;若基体材料为塑性硬化,可能发生的破坏模式则为整体弹/塑性屈曲及面板弹/塑性起皱。在同等质量下,通过材料及几何尺寸的设计,可以最大程度地提高金属波纹夹芯板的面内压缩承载能力,实现结构性能最优化的目的。在较小的面内载荷下,优化后的波纹夹芯结构性能可媲美帽型加筋结构;载荷较大时,波纹夹芯结构的质量优势稍有减小,但由于其抗冲击、减振、散热等多功能特性,仍然具有潜在的实际工程应用价值。

为进一步提高金属波纹夹芯梁的面内压缩性能,提高其整体及局部抗屈曲性能,同时满足其隔热保温性能的需要,本文考虑在波纹芯体空隙中填充泡沫材料(见图1a),以改善波纹夹芯结构的稳定性,提高破坏强度。目前,关于泡沫填充波纹夹芯结构的面内压缩行为研究(见图1b),国内外鲜有报道。为保证在相同质量下提高泡沫填充波纹夹芯梁面内压缩性能,本文采用理论分析与数值模拟(有限元分析)相结合的方法,充分考虑结构在面内压缩载荷下可能发生的破坏模式,对泡沫填充物、波纹夹芯梁对应的几何构型等进行合理的优化设计,以选取最优材料搭配和最优构型。

1 破坏模式理论分析

泡沫填充波纹夹芯梁的面内压缩响应行为与结构的整体尺寸、芯体的拓扑结构以及结构所用材料的力学性能等直接相关。结构总体长度为L,宽度为b,上下面板的厚度为ts,波纹板长度为l、厚度为t,为钎焊焊接预留的波纹平台宽度为f,波纹倾角为θ,如图2所示。

图2 泡沫填充波纹夹芯结构单胞示意图

芯体与面板均采用考虑塑性硬化的304不锈钢,泡沫填充材料选用Rohacell 51聚酯泡沫,相关材料性能见表1,304不锈钢的塑性强化曲线见参考文献[4]。芯体与面板之间采用钎焊方式连接,泡沫与面板和波纹芯体板之间采用环氧树脂胶结。在垂直于波纹方向的面内压缩载荷作用下,假定波纹芯体与面板、波纹芯体板与泡沫、泡沫与面板之间理想连接,不发生脱粘破坏[2-3],则泡沫填充波纹夹芯板可能发生的破坏模式为宏观弹性屈曲、宏观塑性屈曲、面板弹性起皱、面板塑性起皱、芯体弹性剪切破坏,图3给出了前3种破坏模式的示意图。针对不同的破坏模式,本文建立理论模型以预测与之对应的极限载荷,而结构的承载能力取决于极限载荷最低的破坏模式。

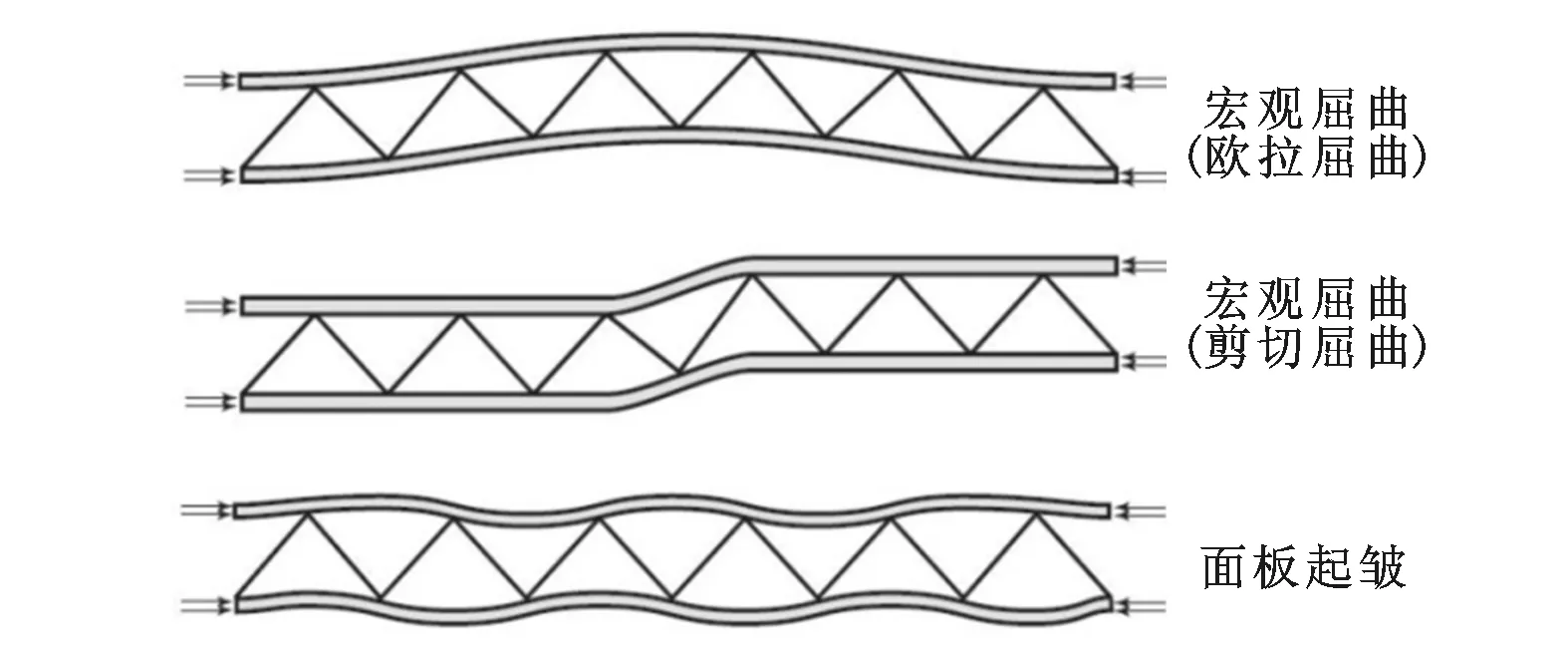
图3 破坏模式示意图[3]

脱粘失效是夹芯结构的最典型失效模式之一,在弯曲和剪切载荷下尤为普遍。本文假定各界面均为理想连接,无脱粘破坏,主要基于以下考虑。

(1)本文考虑304不锈钢波纹夹芯板,芯体板与面板之间通过钎焊连接。由于预留的波纹芯体平台提供了一定的焊接面积,钎焊焊接可以保证芯体和面板之间较高的连接强度,胶结也为泡沫与面板和波纹芯体板之间提供了一定的连接强度,可避免脱粘或脱焊的过早发生[2-3]。

(2)在本文考虑的面内压缩载荷作用下,载荷主要由面板的压缩变形承担,芯体与面板连接处的剪切变形很小(可忽略不计)。因此,对采用钎焊焊接的波纹夹芯板而言,脱粘破坏通常不会作为初始破坏发生。

(3)在初始破坏发生后的大变形阶段,由于弯曲/剪切变形以及芯体与面板变形的不协调,有可能发生脱粘破坏,但本文仅研究初始破坏模式,不考虑初始破坏发生后的大变形,故假定初始结构的各界面为理想连接,无脱粘破坏。

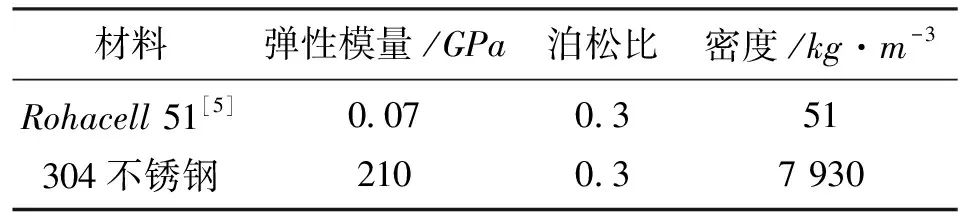
表1 材料基本性能

1.1 宏观屈曲

在面内压缩载荷下,欧拉屈曲和芯体剪切破坏是泡沫填充波纹夹芯板宏观整体失稳破坏的两种主要模式,而这两种破坏模式常常是相互耦合的。假设弯曲由面板承担,剪切由芯体承担,则结构宏观整体屈曲破坏的理论公式为[6-7]

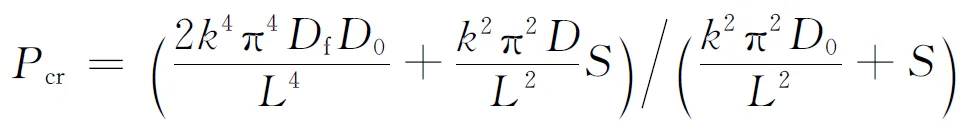
(1)

式中:k是修正系数,由边界条件决定,本文假设为固支边界条件,则k=2;抗弯刚度

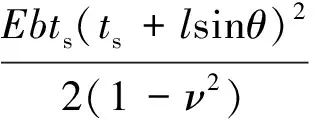
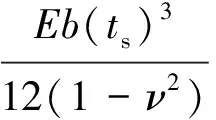
D=2Df+D0

(2)

芯体的抗剪刚度

(3)

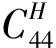
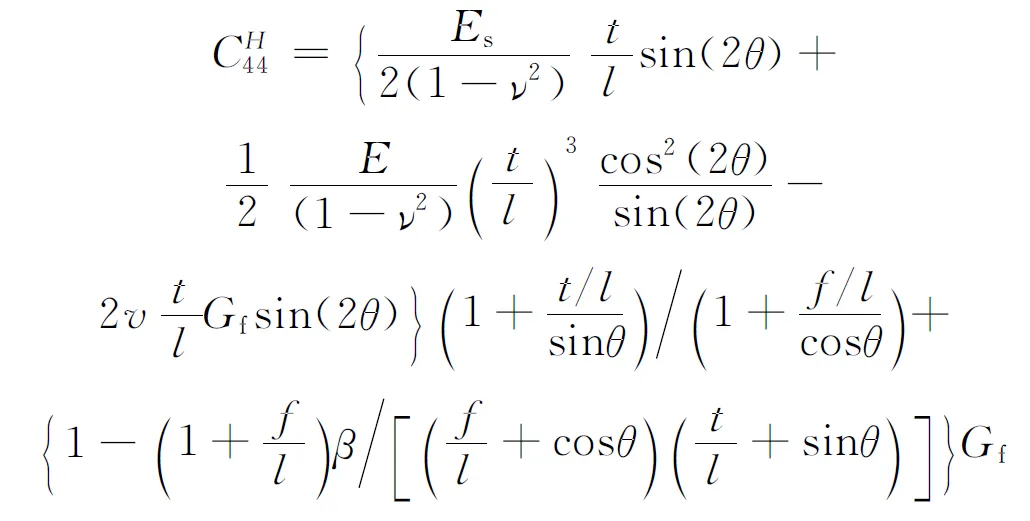
(4)

利用式(1)和式(2),结构的宏观弹性屈曲需满足条件

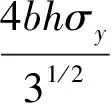
(5)

式中:2σy/31/2是平面应变下材料的屈服应力。若不能满足式(5)条件,结构将进入宏观塑性屈曲阶段,相关载荷计算仍采用式(2),仅需将其中的弹性模量改为相应的Shanley切线模量[9]:以切线模量Et替换平面应变下的弹性模量E/(1-ν2),而Et≡dσs/dεs为平面应变下真实应力与对数应变所形成曲线在σs=Pcr/2bts处对应的切线模量。实际计算时采用迭代算法得到结构的整体塑性屈曲失效载荷。在这个过程中,由于泡沫实际上不是主要承受载荷的构件,因此假设式(3)中的芯体剪切刚度一直保持为弹性状态。

1.2 面板起皱

面板起皱是一种局部失稳破坏模式,通常发生在波纹芯体中两个相邻平台区之间的面板部分。其边界条件取决于波纹芯体与上下面板的粘结情况,一般可假设为固支[3]。为增加波纹芯体与上下面板之间的焊接面积,本文考虑的波纹芯体存在入平台区(图2),波纹与上下面板之间的接触可视为完全焊接,故采用固支边界条件较为合理。

如图2所示,假定可能发生面板起皱的部位为上下面板中长度为p的区域。考虑泡沫填充对面板的支撑作用,可将泡沫等效为Winkler弹性基[5],与此相对应的等效弹簧系数为

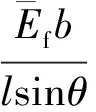
(6)

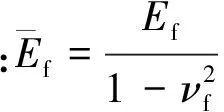
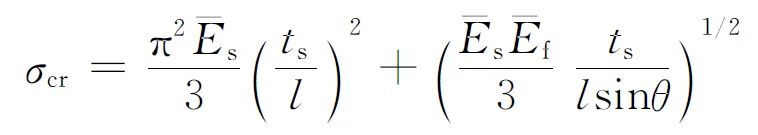
(7)

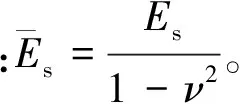
(8)

类似于宏观塑性屈曲,可采用迭代算法求解塑性面板起皱对应的临界载荷。

1.3 破坏模式图

针对受面内压缩的泡沫填充波纹夹芯梁,利用上述理论公式可构造相应的破坏模式图。固定芯体的几何尺寸(即t、l、f、θ固定不变),上下面板的几何尺寸ts、L为变量。为使结果具有普遍性,对变量进行归一化,即采用ts/l、L/l作为变量。

图4 泡沫填充波纹夹芯结构在面内压缩下的破坏模式图

2 有限元计算

为验证本文理论模型的可靠性,采用有限元方法针对面内压缩下泡沫填充波纹夹芯梁可能发生的典型破坏模式及其对应的极限载荷进行验证。

使用商用有限元软件ABAQUS对泡沫填充波纹夹芯结构的面内压缩行为进行数值求解分析,各部分几何模型的单元划分均采用平面应变实体单元(CPE4R)。为保持与理论模型一致,有限元模型中各部分之间的连接假设为完美连接:泡沫填充物与波纹芯体之间,泡沫填充物与上下面板之间,波纹芯体与上下面板之间,以及整体结构与两端的解析刚体之间的约束均采用Tie理想连接约束。

计算时采用准静态位移加载方式,夹芯梁一端采用固支边界条件,另一端除梁的轴向平动自由度约束外,其他自由度全部约束。由于波纹夹芯梁沿其中轴线表现为非对称,足以在面内加载计算时引入屈曲的倾向,故无需额外添加几何缺陷来保证计算结果的稳定性。

考虑到不同破坏模式对应的几何构型不同,本文分别针对不同几何构型的计算进行了网格收敛性分析,以保证计算结果的收敛性。

3 结果分析

结合图4,针对面板塑性起皱、结构宏观弹性屈曲和结构宏观塑性屈曲3种典型破坏模式进行有限元计算验证。根据破坏模式图,针对每种破坏模式,选取典型的几何构型进行分析讨论。

3.1 面板塑性起皱

为通过有限元计算捕捉面板塑性起皱破坏模式(Plastic Face Wrinkling),选用图4中的结构a,其包含6个单胞,几何尺寸为ts=0.67 mm,L=96.85mm。图5给出了面板塑性起皱对应的有限元计算结果及其变形模式。比较发现,数值模拟得到的破坏模式与理论预测一致,载荷的相对误差仅为1.61%。

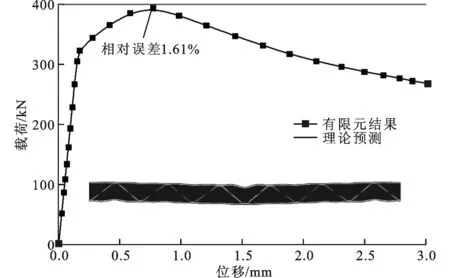
图5 泡沫填充波纹夹芯结构的面板塑性起皱

在面板塑性起皱破坏模式区中,由于图4中的结构a所处的区域相对较为开阔,在其他几何参数不变的情况下分别选取不同梁的长度,进一步考虑了包含5、7、8个完整单胞的情况。计算结果表明,在选取6个单胞几何构型的情况下,可以忽略边界效应对计算结果的影响。

3.2 宏观塑性屈曲

为通过有限元计算捕捉泡沫填充波纹夹芯梁的宏观塑性屈曲破坏模式(Macro Plastic Wrinkling),选用图4中的结构b,其包含17个单胞,几何尺寸为ts=2 mm,L=274.42 mm,结果如图6所示,可见数值模拟得到的宏观塑性屈曲破坏模式与理论预测吻合,且面内压缩强度与理论预测结果的误差为7.67%,属于工程可接受范围。

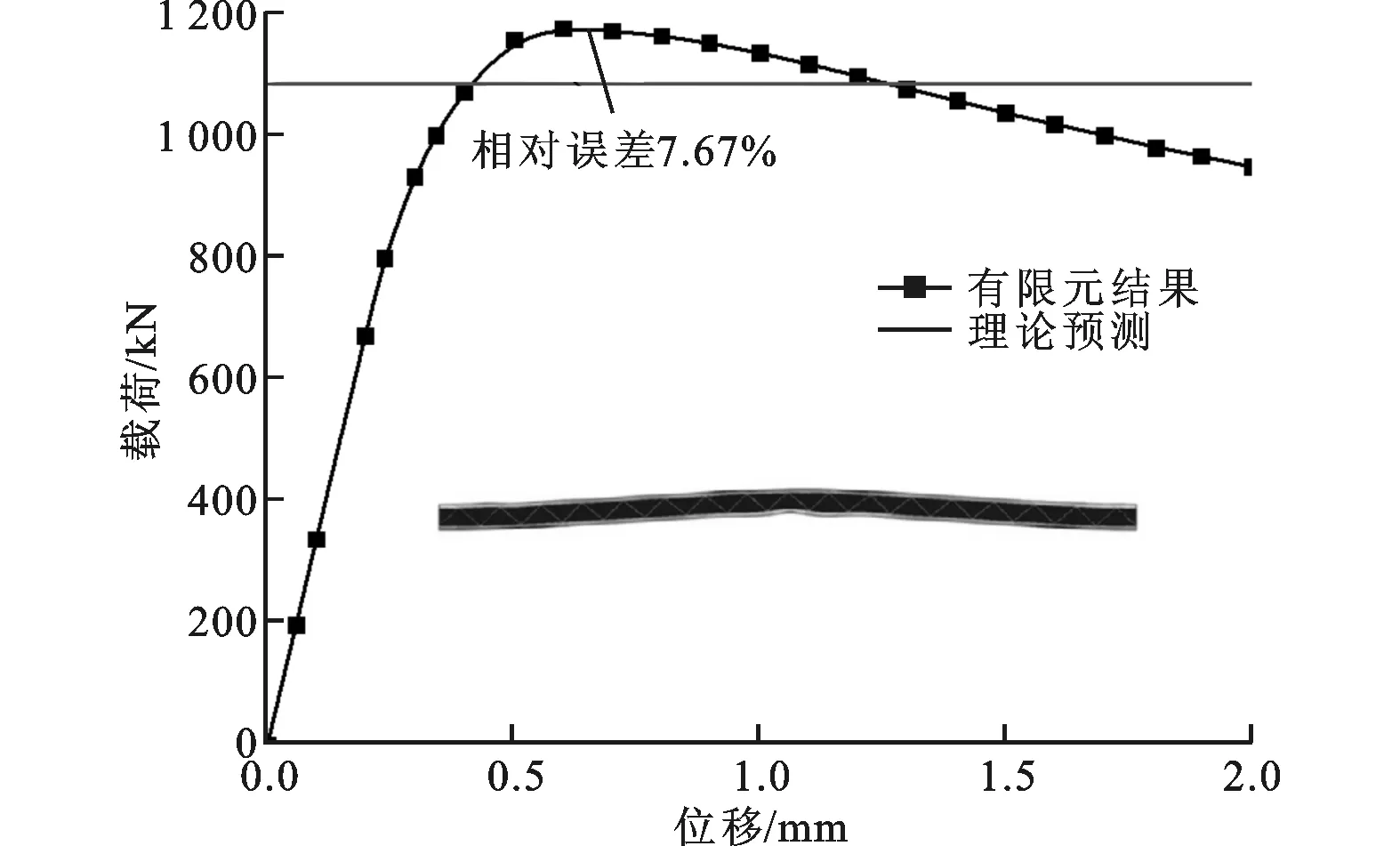
图6 泡沫填充波纹夹芯结构的宏观塑性屈曲

3.3 宏观弹性屈曲

为进一步利用有限元计算捕捉泡沫填充波纹夹芯梁的宏观弹性屈曲破坏模式(Macro Elastic Buckling),选用图4中的结构c,其包含55个单胞,几何尺寸为ts=0.5mm,L=887.82 mm,结果见图7。与其他2种破坏模式相类似,无论是破坏模式还是面内压缩强度,有限元模拟结果均与理论预测吻合良好。

图5～图7给出的有限元结果不仅验证了本文理论预测的有效性,同时还表明有限元模型及方法的可靠性,为进一步指导泡沫填充波纹夹芯结构的优化设计和实际应用奠定了可靠的理论基础。

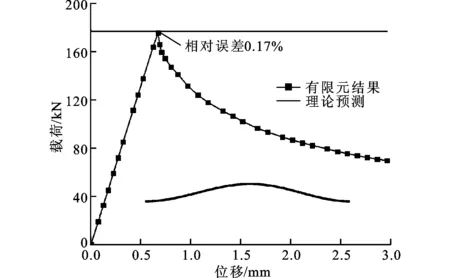
图7 泡沫填充波纹夹芯结构的宏观弹性屈曲

4 最小质量优化设计

在上述理论预测及有限元验证基础上,本节针对泡沫填充波纹复合夹芯结构开展给定面内载荷下的最小质量优化设计,并将结果与空心波纹点阵结构、帽型加筋结构以及金字塔点阵结构进行比较。

最优质量设计以上下面板的厚度、波纹芯体的厚度、腹板长度、腹板倾斜角度以及芯体平台长度为设计变量。在优化过程中,考虑到结构的厚度b对优化结果无实质影响,故保持结构为单位厚度。上下面板与波纹芯体均采用304不锈钢,泡沫采用Rohacell 51。

定义归一化面内载荷为

(9)

结构的质量为

M=ρLb(2ts+lsinθλ)+ρfLblsinθ(1-λ)

(10)

式中:ρ为上下面板所用材料的密度;ρf为泡沫材料的密度;λ表示波纹芯体所占的体积百分比。定义归一化质量为

(11)

归一化几何参量定义为

(12)

本文采用序列二次规划算法,采用Matlab软件进行质量最优化分析,约束条件为结构在面内压缩下不发生面板塑性起皱、宏观弹性屈曲、宏观塑性屈曲等破坏模式。固定f=0,θ=π/4,质量最优化结果见图8,其中空心波纹夹芯、帽型加筋、金字塔夹芯的优化工作分别由Biagi等[3]、Budiansky[10]、Cté等[11]完成。帽型加筋结构承受垂直于加强筋的面内压缩载荷时,结构等效为单一板结构的受载,不具备优化的价值,故图8仅给出该结构承受平行于加强筋方向的面内压缩载荷时的优化结果。

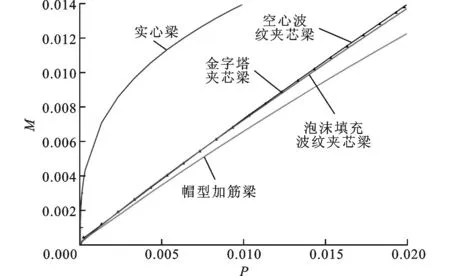
图8 面内压缩下几种梁结构的质量最优化结果比较

从图8可以看出,相同载荷下,泡沫填充波纹夹芯结构相较于空心波纹点阵夹芯结构更具优势，但整体而言,帽型加筋结构的质量优势明显。

为进一步研究平台宽度和波纹倾角对泡沫填充波纹夹芯结构最小质量的影响,图9给出了优化结果对f/L和θ的敏感性分析。

波纹芯体的平台区对结构的承载能力贡献很小,其主要作用是保证制造过程中芯体与面板的有效结合,防止结构出现脱焊等破坏情况。从图9a可以看出,在保证芯体与面板完好连接的情况下,波纹平台的宽度越小越好,f=0时质量为最优。

图9b的结果表明,泡沫填充波纹夹芯的质量最优化结果对波纹倾角θ在[π/6,π/3]范围内的变化并不敏感。进一步比较发现,θ=55°对应的结构质量为最优。

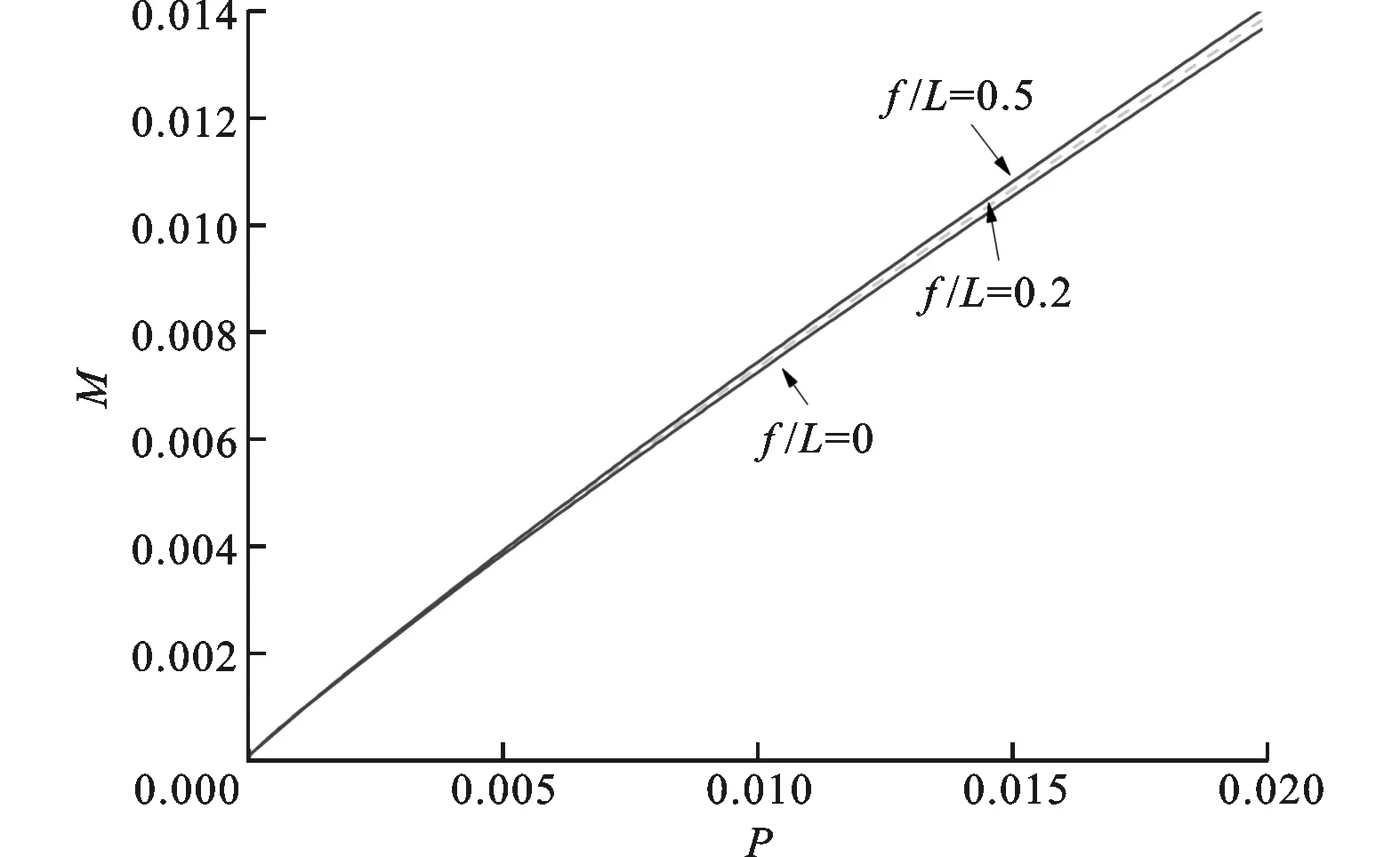
(a)波纹平台宽度的影响

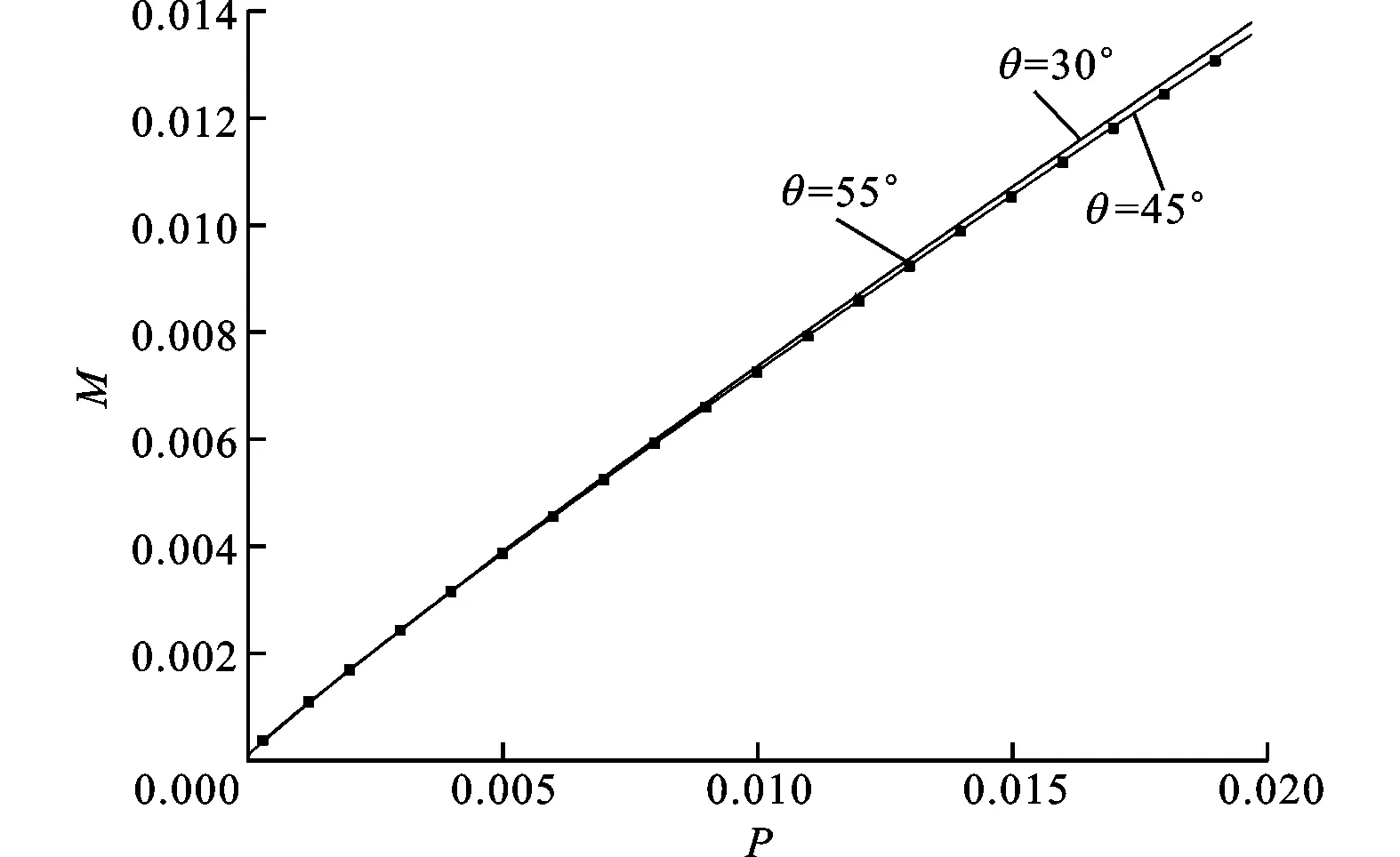
(b)波纹腹板倾角的影响

5 结 论

针对泡沫填充波纹复合夹芯梁结构,采用理论和数值模拟相结合的手段,研究了其在承受垂直于波纹方向的面内压缩载荷作用下的破坏行为,开展了结构最小质量优化设计。结构的破坏模式归纳为整体弹性屈曲、整体塑性屈曲、面板弹性起皱、面板塑性起皱、芯体弹性剪切破坏5种模式。有限元计算结果验证了理论预测的可靠性。比较最小质量优化结果发现,泡沫填充波纹复合结构略优于空心波纹结构及金字塔点阵结构,稍弱于传统的帽型加筋结构。综合考虑承载、能量吸收、减振、隔热等多功能特性,泡沫填充波纹复合结构具有潜在的重要工程应用价值。

[1] 卢天健,何德坪,陈常青,等.超轻多孔金属材料的多功能特性及应用 [J].力学进展, 2006, 36(4): 517-535.

LU Tianjian, HE Deping, CHEN Changqing, et al.The multi-functionality of ultra-light porous metals and their applications [J].Advances in Mechanics, 2006, 36(4): 517-535.

[2] BIAGI R, LIM J Y, BART-SMITH H.In-plane compression response of extruded aluminum 6061-T6 corrugated core sandwich columns [J].Journal of the American Ceramic Society, 2011, 94(S1): 76-84.

[3] BIAGI R, BART-SMITH H.In-plane column response of metallic corrugated core sandwich panels [J].International Journal of Solids and Structures, 2012, 49(26): 3901-3914.

[4] COTE F, DESHPANDE V S, FLECK N A, et al.The compressive and shear responses of corrugated and diamond lattice materials [J].International Journal of Solids and Structure, 2006, 43(20): 6220-6242.

[5] LIU Tao, DENG Zichen, LU Tianjian.Analytical modeling and finite element simulation of the plastic collapse of sandwich beams with pin-reinforced foam cores [J].International Journal of Solids and Structures, 2008, 45(18/19): 5127-5151.

[6] ALLEN H.Analysis and design of structural sandwich panels [M].Oxford, UK: Pergamon Press, 1969.

[7] ZENKERT D.An introduction to sandwich construction [M].London, UK: Engineering Materials Advisory Services, 1997.

[8] YAN Leilei, HAN Bin, YU Bo, et al.Three-point bending of sandwich beams with aluminum foam-filled corrugated cores [J].Materials and Design, 2014, 60: 510-519.

[9] SHANLEY F R.Inelastic column theory [J].Journal of the Aeronautical Sciences, 1947, 14(5): 261-268.

[10]BUDIANSKY B.On the minimum weights of compression structures [J].International Journal of Solids and Structures, 1999, 36(24): 3677-3708.

[11]COTE F, BIAGI R, BART-SMITH H, et al.Structural response of pyramidal core sandwich columns [J].International Journal of Solids and Structures, 2007, 44(10): 3533-3556.

(编辑 赵炜)

CollapseMechanismAnalysisofFoam-FilledCorrugatedSandwichBeamsunderIn-PlaneCompression

HAN Bin1,2,WEN Can1,2,YU Bo1,2,NI Changye1,2,QIN Keke1,2,ZHANG Qiancheng1,2,LU Tianjian1,2,CI Jun3,GENG Li4

(1.Multidisciplinary Research Center for Lightweight Structures and Materials, Xi’an Jiaotong University, Xi’an 710049, China;2.State Key Laboratory for Mechanical Structure Strength and Vibration, Xi’an Jiaotong University, Xi’an 710049, China;3.Guangdong Xi’an Jiaotong University Academy, Foshan, Guangdong 528300, China; 4.Dongguan Yongqiang Vehicles Manufacturing Co.Ltd., Dongguan, Guangdong 523407, China)

It is proposed to insert polymer foams into the interstices of the corrugated core and the collapse of foam-filled corrugated sandwich beams subject to in-plane compression is investigated analytically and numerically to enhance the in-plane compression structural stability of the corrugated sandwich constructions that will be used as a kind of novel lightweight hulls for high speed strains and oil tanks.Failure mechanisms such as global elastic/plastic buckling and elastic/plastic face wrinkling are taken into account.The equivalent elastic constants of the foam-filled corrugations based upon the homogenization approach are employed to calculate the critical failure load of global buckling, and analytical formulae of face wrinkling are given by treating the foam insertion as Winkler-type elastic foundation.A failure mechanism map is constructed by using the material properties of 304 stainless steel and Rohacell 51 foam, and then three different constructions are designed to numerically probe different failure modes.It is shown that the analytical predictions accurately capture both the critical failure load and the failure mechanism.The minimum weight optimization design to foam-filled corrugated sandwich beams subject to in-plane compression is carried out and compared with competitive structures to obtain the optimal geometrical dimension of structure.Comparisons on considering the features such as load bearing, energy absorption, vibration damping, heat insulation and other multi-functional characteristics show that the foam-filled corrugated sandwich has greater potential in engineering application over empty corrugated and pyramidal sandwiches.

tanker; foam-filled corrugated sandwich beams; collapse modes; buckling;optimization

2014-06-23。

韩宾(1986—),男,博士生;卢天健(通信作者),男,教授,博士生导师。

广东省科技厅粤港关键领域重点突破项目(2011A091200008);国家自然科学基金资助项目(11102152,11072188);中央高校基本科研业务费资助项目(xjj2011007)。

时间:2014-08-13

10.7652/xjtuxb201411007

TH117.5

:A

:0253-987X(2014)11-0037-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140813.1008.005.html