用函数变换设计速度传感反馈地震计

黄 敏， 杨晓源， 邵玉平

（四川省地震局， 成都 610041）

0 前言

众所周知， 地震波传到观测台站， 依靠各种地震仪来接收并记录， 地震仪的观测频带下限主要由地震计的工作阻尼常数和工作周期来决定。因此应根据所需要观测的地震波的频段， 适当选择地震计的工作参数（固有周期T 和组尼常数D）可以尽可能完整的反映出所需研究的地面的振动。 短周期地震计主要用于观测地方性的微小地震。 而用速度传感器设计的反馈式短周期的地震计的工作参数稳定性不好， 是国内外观测实践都证实了的问题。 德国地震学家彼得·鲍曼提出：虽然， 短周期仪器参数被认为更稳定， 但经验表明其特征周期与衰减（即工作周期与工作阻尼）随时间变化达几十个百分比[1]。 现有的速度传感反馈地震计产品的参数稳定性不好， 尤其是经过在台站使用数年仅标定不调整的工作模式后， 地震计相关参数的现场测试值与出厂标称值之间的偏差高达10%以上。 有的产品工作参偏差数甚至接近30%[2]。

速度传感反馈地震计产品的工作参数偏差较大是因为该地震计中的负反馈环是一个浅反馈环。 由浅反馈环生成的工作周期和工作阻尼既与反馈电路参数有关， 又与机械摆的参数相关。 影响这两个工作参数的因素与部件非常多， 在常温范围和长期工作的老化中极难有效控制它们带来的飘移。

1 解决思路探讨

1.1 加深反馈深度不能寄希望于改变机械摆的参数

理论与实践都已经证明， 机械摆的固有频率越高， 反馈式地震计的自身噪声就越大。 过大的自身噪声不利观测微小地震， 然而反馈式短周期地震计的主要用途就是用于观测地方性的微小地震。 这也是我国流行的反馈式短周期地震计产品均采用速度传感方案的缘由， 为限制自身噪声在规定的频段内低于规范值， 流行产品中机械摆固有频率参数为3 Hz。 正因为如此， 虽然也有机械摆固有频率为6 Hz 的产品， 因其自身噪声参数不满足规范要求故仅有较少用户选用。 短周期速度反馈地震计的原理是用负反馈将机械摆的周期延长， 其反馈深度取决于反馈前后的周期比， 即机械摆的固有周期与闭环工作周期之比。 考虑到地震计自身的噪声限制， 不能采用提高机械摆的固有频率的方法来加深负反馈深度。

1.2 利用深度负反馈来实现

我国现有的反馈式短周期地震计产品， 其工作周期多为1 s 或2 s。 反馈式短周期地震计中的核心部件-机械摆， 其固有频率多取3～6 Hz， 对应的固有周期为0.33～0.167 s。 反馈前后的周期比最大为12， 最小只有3。 鉴于此， 常用的速度传感反馈地震计产品仅仅是一个反馈深度很浅的负反馈环。 而浅负反馈环带来的不利因素在于反馈地震计的工作参数（如工作周期、 工作阻尼以及灵敏度）， 将受到反馈环路内众多因素的影响， 从而导致工作参数的稳定性欠佳。

在观测实践中我们知道， 使用深反馈的位移传感反馈地震计在大于5 Hz 的地震观测频段高端的噪声较大， 而其工作参数偏差却仅有2%左右。这就启发我们在速度传感反馈地震计采用加大负反馈的深度， 使地震计的工作周期与工作阻尼仅与少数几个电阻电容的数值相关的技术途径。 本人在参与某反馈式短周期地震计产品的设计中就采用了这一技术思路， 力图解决速度传感反馈地震计工作参数稳定性太差、 与标称值偏差太大的问题。

2 设计方案分析

2.1 函数变换方案允许负反馈的深度

为了解决反馈式短周期地震计工作参数稳定性的问题， 设计中我们有意识地加大了负反馈环的反馈深度。 但在速度传感反馈地震计中有一个众所周知的规律， 就是反馈深度越大， 地震计闭环工作周期与机械摆的固有周期之比就越大。 在机械摆的固有周期一定的前提下， 较大的负反馈深度将使反馈生成的闭环周期远大于我们所需的工作周期， 无法满足既定的参数指标。 因此， 我们采用一种新的方案——函数变换， 来设计速度传感反馈式短周期地震计。 该方案的要点是机械摆的固有频率仍保持为3 Hz 不变， 以确保地震计的自身噪声水平不变， 通过加大反馈的深度来提高工作参数稳定性。 由于加大反馈深度后生成的闭环周期和闭环阻尼不再是产品所需的最终参数，仅为中间的过渡参数。 该过渡参数的闭环周期和闭环阻尼可以设计为远大于地震计最终的工作周期和工作阻尼。 为了得到所需工作参数的地震计，采取了在闭环反馈环外通过双二阶函数变换电路消去该过渡的闭环周期和阻尼， 并同时生成了地震计的工作周期与阻尼的方案。

2.2 反馈深度与动态范围扩展分析

在速度传感反馈地震计中， 地动速度输入V（S）与机械摆振动中心位移XC（S）之间满足下列关系式：

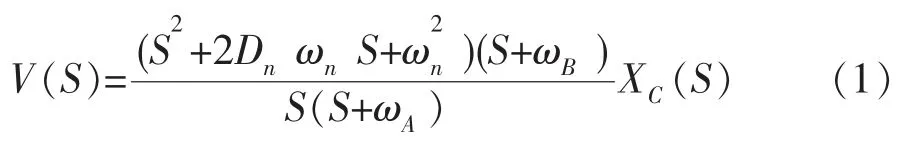
式（1）中， ωn为反馈地震计闭环角频率， 单位1/s；Dn为反馈地震计的闭环阻尼， 无量纲； ωA为一阶环路滤波器的极点绝对值， 单位1/s； ωB为反馈地震计闭环生成的一阶项角频率， 单位1/s； 当一阶环路滤波器为一阶高通电路时， ωA和ωB与反馈地震计的开环角频率ω0开环阻尼D1闭环角频率ωn和闭环阻尼Dn之间满足下列关系式：

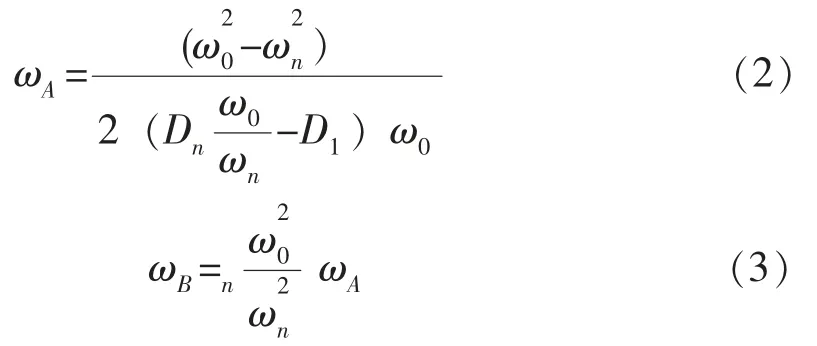
在计算速度传感反馈地震计动态范围上限时，认为地震计是一个机械摆振动中心位移XC（S）受限的系统， 这一假设符合速度传感反馈式地震计正常工作时的实际状况。 因为振动中位移过大， 传感线圈运动将越出磁隙磁感应强度分布较均匀的区域， 造成非线性失真急剧增大。 在图1 中， 假设了振动中心位移在平衡位置附近的最大位移Xcm为0.1 mm， 据式（1）计算允许输入的最大地动位移Vcm输入曲线。 计算上述曲线簇时， 假设了机械摆的固有频率为2 Hz、 开环阻尼为1。 为了与未施加反馈时的同一机械摆的动态范围上限作比较，图中还绘出了机械摆在阻尼为0.7 的曲线。 该曲线按照式（4）绘制。

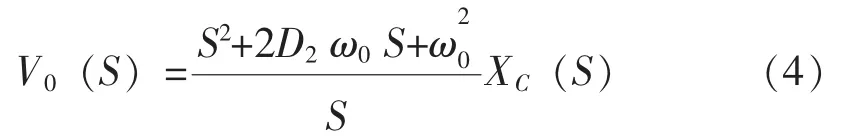
图1 中仅有的一条水平直线是根据反馈地震计最大单端输出峰值为10 V 和单端灵敏度为1 000 VS/m 绘制的因输出电压受限的动态范围上限以资比较。

采用函数变换方案加大了反馈地震计的负反馈深度， 同时也扩展了机械摆的动态范围上限。如下图所示， 给出了一个固有频率f0=3 Hz 的机械摆振动中心位移受限（假设为0.2 mm）的动态范围扩展曲线。

该机械摆是采用了一阶高通环路滤波作为闭环反馈的， 绘制该曲线时假设了机械摆的振动中心允许的最大位移为0.2 mm。 图1 中Tn=2 s 曲线表示用一阶高通环将其直接反馈为2 s 地震计的动态范围上限， 不经过函数变换。 Tn=4 s、 Tn=8 s 则表示采用一阶高通环路分别将闭环周期分别延长到相应的4 s、 8 s， 然后通过函数变换变至2 s 时的机械摆动态范围上限曲线。

由图1 可见， 闭环周期与设计所需的工作周期之比越大， 机械摆的动态范围上限扩展越大。图1 中还给出了反馈地震计输出电压受限于电源电压单端最大不失真输出为10 V 时的动态范围上限。 在地震计单端电压灵敏度为1 000 VS/m 时，该曲线是地动速度为0.01 m/s 的水平线。

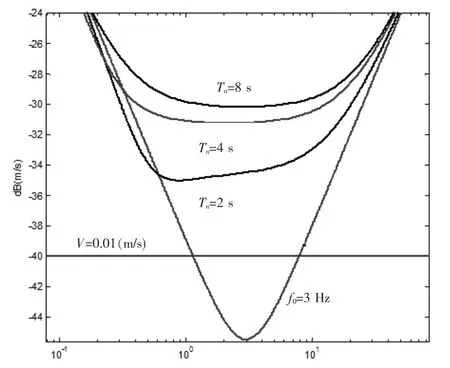
图1 固有频率f0=3 Hz 的机械摆振动中心位移受限的动态范围扩展曲线Fig.1 Extended dynamic range curve of mechanical vibration center displacement limited with inherent frequency f0 of 3 Hz

2.3 闭环周期、 闭环阻尼与变换周期相关性分析

在函数变换方案中， 虽然工作周期和工作阻尼仅与变换电路中的两个电阻和电容有关， 完全与机械摆的参数无关， 但是闭环生成的中间参数仍然受到机械摆参数的影响。 而机械摆的参数又是最易受环境条件影响和老化而有所变化。 当机械摆参数变化闭环反馈生成的中间过渡参数必然随之变化， 导致了函数变换电路中与其对消的二阶零点不能完全对准而有所残留。 下面给出上述两者不能完全对准时对系统幅频特性造成影响的理论分析结果。

闭环周期和闭环阻尼变 对幅频特性的影响，可通过下面几种情况的分析得到。 首先观察固定闭环阻尼Dn保持不变， 闭环周期与变换周期之比为4 的条件下， 闭环周期Tn在设计值8 s 变化10%时， 系统的幅频特性变化情况如图2 所示； 同样地在固定闭环周期Tn保持不变， 闭环周期与变换周期之比为4 的条件下， 闭环阻尼Dn在设计值1.560 26 变化10%时， 系统的幅频特性变化情况如图3 所示。其次观察固定闭环阻尼Dn保持不变， 闭环周期与变换周期之比为2 的条件下， 闭环周期Tn在设计值4 s 变化10%时， 系统的幅频特性变化情况（图4）； 同样地固定闭环周期Tn保持不变， 在闭环周期与变换周期之比为2 的条件下， 闭环阻尼Dn在设计值0.883 88 变化10%时， 系统的幅频特性变化情况如图5 所示。

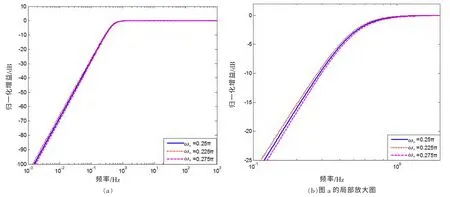
图2 周期之比为4， 闭环周期变化10%时系统的幅频特性差异图Fig.2 Amplitude frequency characteristics difference diagram with period ratio of 4 and closed-loop period change±10%

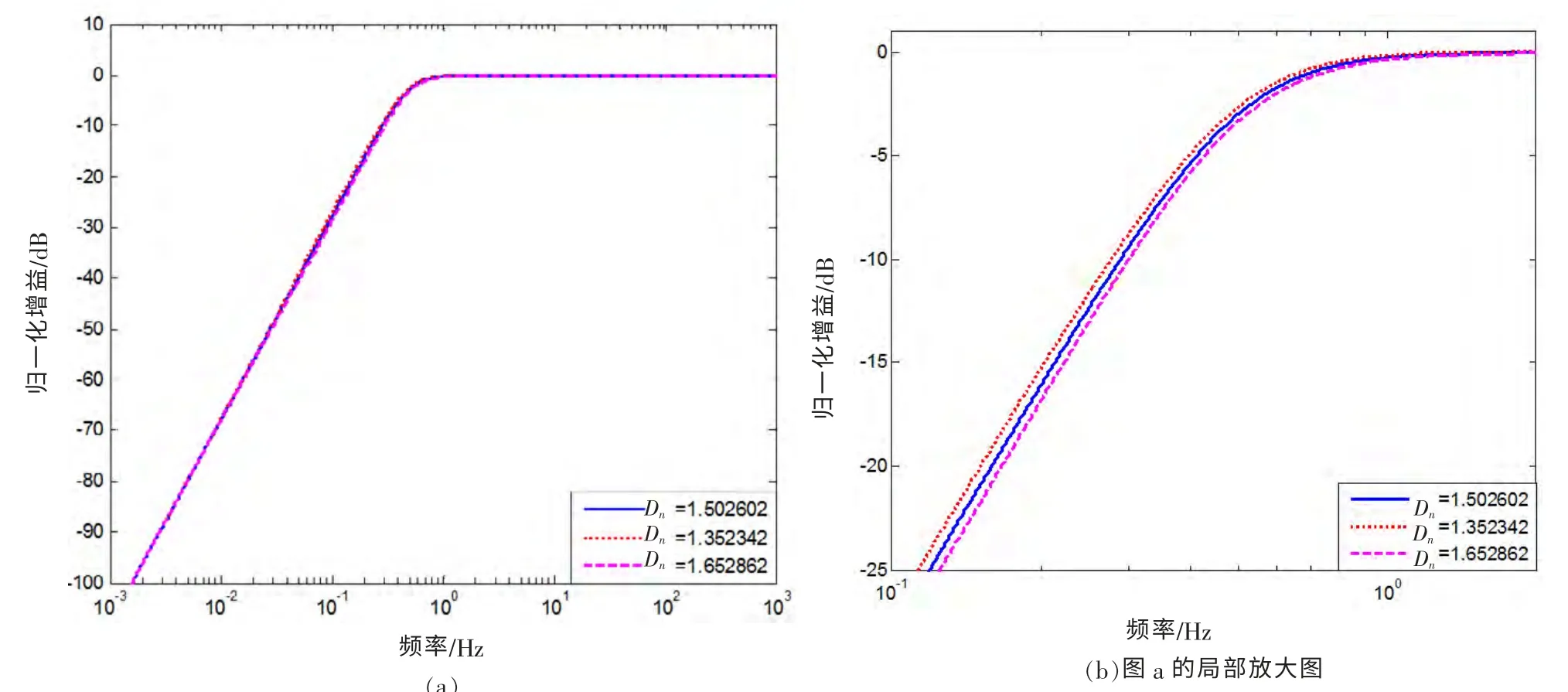
图3 周期之比为4 的条件下，闭环阻尼Dn 变化 10%时系统的幅频特性对比图Fig.3 Comparison diagram of amplitude frequency characteristics with period ratio of 4 and closed-loop damping Dn change ± 10%

由上述图2 至图5 可见， 闭环周期与变换周期之比越大， 因闭环参数改变带来的通带特性影响越小。 其原因当然是变换比越大被抵消的中间过渡离通带越远。 由函数变换电路生成的工作周期及工作阻尼与机械摆的参数完全无关， 仅取决于变换电路中的两个电阻和两个电容的精度。 从而大大提高了反馈式地震计的参数的稳定性以及灵活性。 即完全可以通过改变形成主导二阶极点的电阻、 电容的数值， 来灵活地改变地震计的工作周期为1 s 或和2 s。

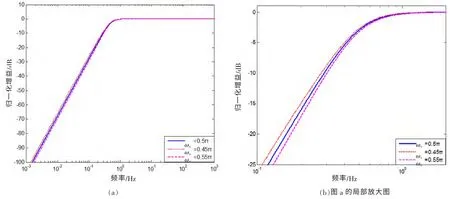
图4 周期之比为2 的条件下， 闭环周期 10%时系统的幅频特性差异图Fig.4 Amplitude frequency characteristics difference diagram with period ratio 2 and closed-loop period change ± 10%

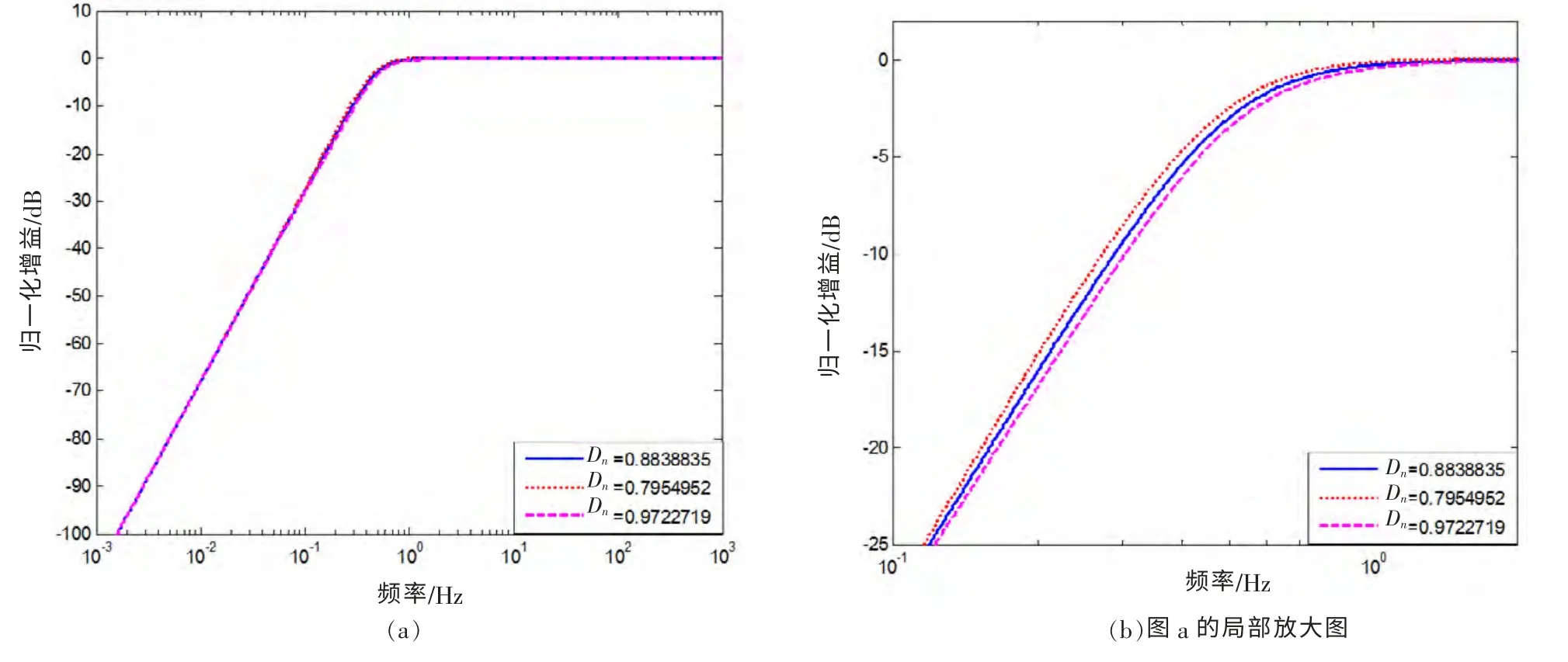
图5 周期之比为2，闭环阻尼Dn 变化10%时系统的幅频特性差异图Fig.5 Comparison diagram of amplitude frequency characteristics with period ratio 2 and closed-loop damping Dn change ± 10%

2.4 函数变换方案优势分析

采用函数变换来设计速度传感反馈式短周期地震计。 该方案的要点是机械摆的固有频率仍保持为3 Hz 不变， 以确保地震计的自身噪声水平不变， 通过加大反馈的深度来确保工作参数稳定性。 由于加大反馈深度后生成的闭环周期和闭环阻尼并非不是产品的最终参数， 仅为中间的过渡参数。 该过渡参数的闭环周期和闭环阻尼可以设计为远大于地震计最终的工作周期和工作阻尼。在闭环反馈环外通过双二阶函数变换电路消去该过渡的闭环周期和阻尼， 并同时生成了地震计的工作周期与阻尼。

此方案的优点之一是加深负反馈， 其二是由闭环反馈生成的闭环周期位于通带外， 即便受到环境变化影响或随时间推移而出现了老化， 其对通带内的幅频特性的影响亦较小。 由函数变换电路生成摆函数的工作周期及工作阻尼与机械摆的参数完全无关， 仅取决于变换电路中的两个电阻和两个电容的精度。 从而大大提高了反馈时地震计的参数的稳定性以及灵活性。 可以通过改变形成摆函数的电阻、 电容的数值来改变地震计的工作周期为1 s 或和2 s。 预期可以做到与采用位移传感器的反馈式宽带地震计误差相当的水平， 即参数偏差可以控制在百分之三到五的量级水平，可优于现有的产品半个数量级。

3 函数变换的实现方法

3.1 地震计最终工作周期传递函数的生成

设计时我们将固有周期为0.33 s 的机械摆，通过负反馈将其周期延长至4.472 s， 该周期即为闭环周期。 闭环形成的传递函数为H1（S）， 显而易见， 由于加大了负反馈深度的原因， 该闭环参数的数值远大于指标要求的2 s 工作周期， 我们通过函数变换H2（S）将H1（S）消除的同时生成最终所需的工作周期的传递函数为H（S）。 框图如下：

图6 传递函数框图Fig.6 Block diagram of transfer function

反馈得到的闭环传递函数如下式：

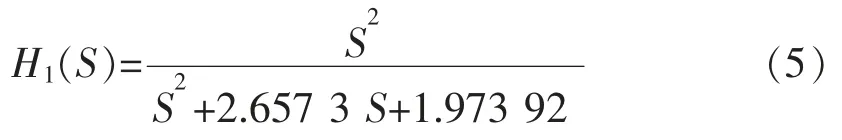
变换电路的传递函数如下式：

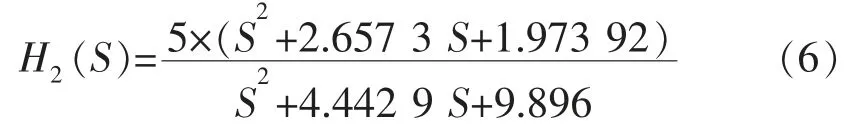
设计所需的传递函数特性图如下式：

在变换电路的传递函数H2（S）函数变换式中，分母的二阶多项式是我们所需的主导二阶极点，所对应的周期为2 s， 阻尼为0.707 1。 分子多项式对应的是闭环周期和闭环阻尼。

将上述传递函数绘制在一张图上（如图7 所示）加以对比分析， 我们可以直观的看到它们之间的关系。

3.2 函数变换简化电路

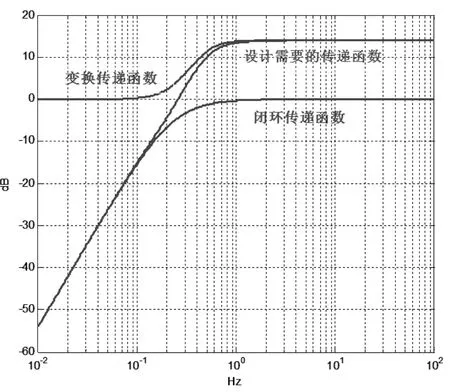
图7 传递函数幅频特性对比Fig.7 The comparison of the amplitude frequency characteristics of transfer function

根据上节的分析结果， 将生成函数变换的电路插入环路输出与地震计输出之间， 只要分子的二阶多项式与闭环生成位于分母的二阶多项式系数相同， 就可以将其影响消除充分几乎不留痕迹。对消后剩余下的分母二阶多项式完全由函数变换电路生成， 仅与电路设计中的两个电阻和两个电容的数值有关， 完全不受稳定性较差的机械摆的参数的影响， 实现了工作参数稳定性较高的目标。只要相关的两个电阻电容选用温度系数小、 老化率低的产品， 预期的工作周期和工作阻尼偏差可以做到位移传感反馈地震计的水平， 即将其偏差控制在2%左右。

二阶函数变换可以用多种RC 有源电路来实现， 为了降低成本和减少精密元件数量， 具体实现时未使用多运放方案， 而采用了简化的单运放方案， 电路如图8 所示。 由图可见， 全部电路仅由一只运放、 两只精密电阻和3 只精密电容构成。其中C1、 C2、 R1、 R2共同决定设计所需的二阶主导极点位置， C3与C1、 C2之比决定被抵消的闭环二阶极点与主导极点的距离。 该比值越大则距离越远， 闭环参数对标定脉冲响应波形的影响越小，系统传递函数测定的精度越高。

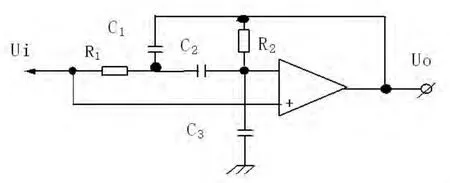
图8 二阶函数变换电路简化图Fig.8 The simplified circuit diagram of two order transfer function

4 使用函数变换设计短周期地震计的观测结果

周期为1 s 的反馈地震计研制成功后， 通过了四川省科学技术委员会主持的鉴定。 鉴定专家组根据省科技情报所提供的查新资料， 认为该反馈地震计使用的函数变换具有新颖性与独创性， 评价为自主创新产品。

该产品周期为1 s 的地震计已经在四川省内水库台网使用多年， 性能稳定， 尤其是在汶川大地震时或是芦山地震， 相关的紫平铺、 瓦屋山、 武都、 瀑布沟等水库地震观测台网都有良好的记录。图9、 图10 为紫坪铺水库地震台网记录的两次地震波形图。

目前， 该产品周期为2 s 的地震计已于用于泸定水库新建地震台网、 武都水库地震台网改建项目， 参数稳定性如何还有待于时间的检验。

应当指出， 位于通带之外的二阶极点虽然对通带幅频特性影响较小， 但由于目前计算工作周期和工作阻尼的计算软件大多都采集了标定响应波形在时域进行计算， 这样就会出现中间参数的偏移会表现为工作参数的偏差。 为解决此问题带来的困惑， 采用邵玉平研发的频域法计算软件来加以处理， 其影响程度会大幅度降低。

图9 汶川地震记录波形（2008年5月12日）Fig.9 Wenchuan earthquake wave(May 12, 2008)

图10日芦山地震记录波形（2013年4月20）Fig.10 Lushan earthquake wave(April 20, 2013

[1] 彼得·鲍曼（德）. 中国地震局监测预报司译. 新地震观测实践手册（第一卷）[M]. 北京： 中国地震出版社，2006.

[2] 杨晓源， 传递函数的精度问题[J]. 地震地磁观测与研究， 2010， 31（6）： 31-39.