DSm组合规则的改进及其在直觉模糊集上的拓展

唐长春，敖志刚，宫云祥，张康益，王有成

解放军理工大学 野战工程学院，南京 210007

DSm组合规则的改进及其在直觉模糊集上的拓展

唐长春，敖志刚，宫云祥，张康益，王有成

解放军理工大学 野战工程学院，南京 210007

随着传感器、网络等微电子和通信技术的深入发展，人们能够获取到的信息呈现爆炸式增长，这对人们处理信息的能力提出了更高要求。多源信息融合技术应运而生，其给人们提供了一条高效、精确应用信息的途径[1]。信息的多源性是信息融合的基础，而信息的不确定性、不完善是信息融合最本质的动因。对于多源不确定信息的融合问题，目前已有很多方法，包括概率论、模糊集、贝叶斯理论、神经网络、DS证据理论（Dempster-Shafer Theory，DST）等，其中DST是一种具有处理不确定信息能力的不精确推理理论[2-4]，在不确定性信息的表示、推理、融合等方面的优势已得到了广泛认同。但DST处理冲突信息的能力不强，对于高度冲突的证据合成结果较差。针对DST的不足，许多学者提出了改进方法。DSmT（Dezert-Smarandache Theory）是由法国的Jean Dezert博士和美国的Florentin Smarandache教授提出和发展的一种将似事而非和自相矛盾推理方法用于信息融合的新理论[5]。DSmT可看作是DST的拓展，其在处理冲突信息和不完善信息等方面的能力得到了明显的加强，因此受到了普遍关注。在实践中，发现DSmT也存在着非常致命的问题，即DSmT的信度组合结果往往很难给决策提供有效的依据，甚至会增加证据源信息原有的不确定性。

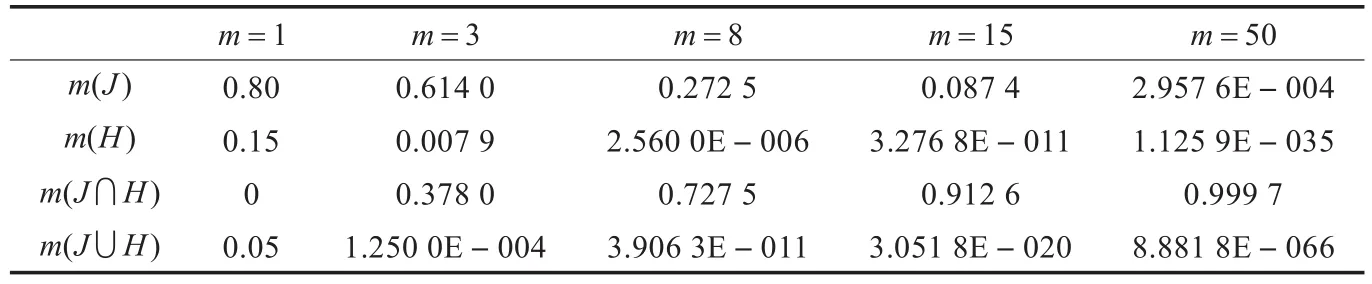
表1 m个传感器识别信息的DSmT组合结果

本文对DSmT及其存在的问题进行了较深入的分析，并在其基础上提出了一种新的基于冲突再分配的证据组合规则（K-DSm规则）。为进一步提高DSmT处理冲突、模糊和不精确信息的能力，研究了DSmT在直觉模糊集上的拓展，将传统的信度赋值函数替换为直觉模糊信度赋值映射，并讨论了直觉模糊拓展后的信度组合规则。最后，通过数值实例对提出的方法进行了验证。

1 DSmT及其存在的问题分析

DSmT对证据理论中的Shafer模型作了修改，提出了DSm模型，该模型定义了一个广义的鉴别框Θ，减少了对鉴别框中焦元的约束限制，允许Θ中的元素存在交集，从而极大提高了DSmT组合冲突信息的能力，并且使其能够有效处理具有模糊边界、不可细分的信息融合问题，如高/矮、胖/廋等。跟DST一样，DSmT也是采用正交和的方式对焦元进行组合，所不同的是，DSm组合规则不需要归一，其中的缘故本质上即是DSm模型保留了所有冲突焦元的信度赋值。DSm组合规则的具体形式如下：

其中，DΘ是由Θ中的命题，以及通过∪和∩运算组成的所有复合命题的集合，称为超幂集。DSm组合规则具有良好的交换性和结合性，符合证据源的合取一致原理；由于这种组合规则不需要归一化过程，从而能够避免出现类似于DST在高冲突情况下产生的问题；相比DST，DSm组合规则的组合结果更符合人类的直觉。在实际应用中，DSmT表现出的优势是明显的，但同时也存在诸多缺陷和不足，先看一个简单的例子：

假设在某次联合训练中，基地上有m个传感器同时监测到某空域出现的目标，各传感器在本地对监测到的数据进行处理后将识别结果发送到联合训练导控中心，以得到一致和准确的预测。假定这m个传感器得到了如下完全一致的结果：

mi(J)=0.8，mi(H)=0.15 ，mi(Θ)=0.05，（i=1，2，…，m，J代表歼击机，H代表轰炸机）

mi(Θ)表示传感器i对未知信息(It=J∪H)的信度赋值。假如联合训练导控中心采用DSmT对这些传感器的识别信息进行组合，m取不同值时得到的结果如表1所示。

本例类似于文献[6]给出的例子。在这个例子中，m个传感器相当于m个证据源。由于这m个证据源完全一致，并且分配给命题J的信度较大，按照正常的逻辑，它们的组合结果应该能够减小信息的不确定性，同时进一步增大命题J的信度。但是，从表1中发现随着证据源数目的增多，组合结果中分配给主焦元的信度不断减小，大量信度赋给了主焦元的交集，这种现象是异常的，特别是命题J的信度逐渐减小趋近于0，违背了人类直觉。显然，根据表1所示的组合结果，难以对目标进行识别。

从上述例子中，可以发现DSmT的一个重要缺陷，即在某些情况下，DSm组合规则的组合结果不但不能减小信息的不确定性，反而会增加信息的不确定性。究其原因，可以从两方面考虑，即模型和组合规则。DSmT建立在DSm模型上，允许鉴别框中的焦元存在交集既是DSm模型的优势，同时又给DSm组合规则带来了隐患。上文提到，DSmT采用正交和规则对焦元的信度进行组合，在这种组合规则下，如果允许保留冲突焦元，那么冲突焦元一经产生，便不会消逝，赋予它的信度也不会被再次分配，只能进行重组、传递和累积[6]，这即是出现上例所示问题的原因。

应用DSmT的另一个困难是其计算复杂度有可能出现组合爆炸现象[7-8]。DSmT对问题的分析和处理建立在DSm模型和超幂集上 DΘ，而 DΘ的势|DΘ|按22|Θ|数量级递增，同时由于组合过程中冲突焦元的累积，会引发焦元呈爆炸式增长，造成计算量和存储量的“爆炸”，当|Θ|＞6时，DΘ的计算和存储将面临极大的困难，并且随着证据源的不断补充，计算的复杂度会进一步提高。

针对DSmT存在的不足，文献[6]提出了一种基于冲突再分配的CR-DSmT组合公式，使组合结果中分配给主焦元的信度得到了合理的增加；文献[9]则提出了一种快速分层递阶DSmT近似推理融合方法，有效提高了算法的计算效率；文献[8]亦研究了优化DSmT计算复杂度的方法；此外，还有许多文献从不同的角度对DSmT进行了改进[10-11]。尽管上述文献都在一定程度上改善了DSmT的相关性能，但它们大多只从单一角度去寻求局部性能上的提高，而忽视了算法整体上的优化，因此，在应用上仍有一定的局限。受经典DST组合规则的归一化过程和文献[6]的启发，本文提出了一种新的基于冲突再分配的信度组合规则，称之为K-DSm组合规则。

2 K-DSm证据组合规则

如何处理冲突是证据理论体系中的一个关键问题。由于大部分组合规则都是采用正交和（析取）的方式来组合证据，而这种方式必定会引起多个相异主焦元的相交（∩）运算，由此便会产生冲突焦元。所谓冲突焦元即是在证据组合过程中，产生的含有交集的焦元，如(θ1∪θ2)∩θ3。由于Shafer模型规定命题之间完全互斥，因此，在DST的组合结果中，冲突焦元的信度赋值始终为0，这是DST处理冲突能力低的本质原因；DSm模型中虽保留了冲突焦元的信度赋值，但却造成了冲突的累积，增加了组合证据的不确定性；Yager将冲突焦元视为不可靠的信息，而将其信度分配给了完全未知集[12]；Dubois和Prade反驳Yager的观点，认为焦元之间的冲突表征的是一种竞争关系，冲突焦元的信度应在主焦元之间进行再分配[13]。实质上，冲突焦元既描述了主焦元之间的异性，同时也蕴含了主焦元之间的共性。如果采用DSm模型，那么两个主焦元之间的交集必然属于两主焦元，即θ1∩θ2⊆θ1且θ1∩θ2⊆θ2，同时，从主观上看交集部分包含的信息是不确定的，逻辑上亦有θ1∩θ2⊆It(It=θ1∪θ2∪…∪θn)。从而，综合Yager和Dubois的观点，本文认为冲突焦元的信度既应属于未知的部分，同时应在主焦元之间进行再分配。并且既然冲突焦元不能提供有用的信息，那么完全可以在组合结果中将其去除，基于此，提出如下所示的K-DSm组合规则。

其中，X∩=X1∩X2∩…∩Xm即表示组合过程产生的冲突焦元，d(X∩)表示冲突焦元 X∩的信度被重复分配的次数，假设在 X∩中，直接与“∪”算子相连的主焦元个数为d∪(X∩)，则：

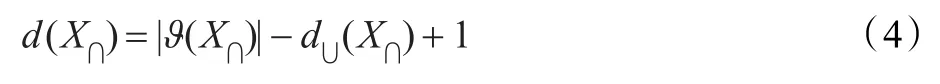
与经典DSm组合规则相比，K-DSm组合规则在组合结果中去除了冲突焦元，这不仅使得计算量和存储量大为减少，同时也使得信度分配更为集中，从而促使主焦元能够获得更多的信度并且更容易收敛。K-DSm组合规则中含有归一化系数K，K有别于DST中的冲突因子，它能够消除由于冲突焦元信度被重复分配而造成的信度溢出，起到弱化冲突的作用。

应用K-DSm组合规则去解决上文中提到的例子时，得到如表2所示的结果。

表2 m个传感器识别信息的K-DSm组合结果

从表2中可以看出，随着证据源的增多，各焦元的信度赋值逐渐收敛。在组合结果中，命题J的信度赋值稍微有所减少，而其他焦元的信度赋值却有所增加，这是因为，在K-DSm组合规则中，各主焦元的地位被视为等同，在组合过程中同等地获得了冲突焦元的信度，在某些情况下，这是不合理的，比如说本例。命题J对冲突焦元的影响显然较大，其在信度分配中理应要占优势，由于这考虑起来比较复杂，将在以后的工作中做进一步研究。尽管K-DSm组合规则也存在着不足，但它的组合结果仍然要优于DSm组合规则，根据表2所示的结果，可以很明确地判定目标为J。应用K-DSm组合规则去解决证据理论中常用的一个例子，即Zadeh问题时，同样得到相比DSm组合规则更符合直觉的结果，进一步说明了K-DSm组合规则的优越性。

3 DSmT在直觉模糊集上的拓展

DST以及DSmT中的基本信度赋值都是一个单一的值，在概念上对应于模糊集理论中的隶属函数，表征证据源对命题的支持程度。多数情况下，证据源不仅能提供支持命题为真的度量，同时也能提供反对命题为真的度量，这就意味着DST或DSmT的信度赋值方式不能完全描述证据源提供的信息，从而造成信息的流失，直接的后果是导致组合结果的精度下降，并且会增加证据源信息之间的冲突。直觉模糊集（Intuitionistic Fuzzy Sets，IFS）[14]同时引入了隶属度、非隶属度和犹豫度三个度量，相比模糊集，其能够更加灵活和完整地描述模糊信息。因此，本文考虑将DSmT中的基本信度赋值扩展为一个直觉模糊数，以此来进一步增加DSmT处理模糊和冲突信度的能力。

定义1设Θ是DSm模型下的广义鉴别框，DΘ是Θ的超幂集，则映射：

根据直觉模糊数的定义，有0≤μΖ(θ)+νΖ(θ)≤1，其中 μΖ(θ)与DSmT中的广义基本信度赋值意义相同，表征证据源对命题θ的支持程度；νΖ(θ)则表示对命题θ的不信任度。同样可以引入犹豫度πΖ(θ)的概念来描述对命题的不确定性度量，并且πΖ(θ)=1-μΖ(θ)-νΖ(θ)。

在DSmT的理论框架下，Bel(θ)是命题θ(θ∈DΘ)的广义信度函数值，表示证据对命题θ完全支持的程度，若θ的余集为θˉ，则Bel(θˉ)表示证据对命题θ完全反对的程度。可以看出，Bel(θˉ)的特征意义与νΖ(θ)是一致的。因此，对于一个由经典DSm模型描述的信息融合问题，可以采用一种简单且有效的方法来对广义基本信度赋值进行扩展，得到直觉模糊信度赋值IFS_bba。方法即是：将μΖ(θ)取值为DSm模型中的广义基本信度赋值m(θ)，νΖ(θ)取值为与之对应的Bel(θˉ)，则mZ(θ)=＜m(θ)，Bel(θˉ)＞，可以证明其是一个合适的IFS_bba。

在给出直觉模糊拓展后的证据组合规则前，先对一些符号进行说明。根据文献[14]可以推出“⊕”和“⊗”算子具有以下的运算关系：

利用上述运算规则和定义的符号，可以方便地给出直觉模糊拓展后的证据组合规则，如下：

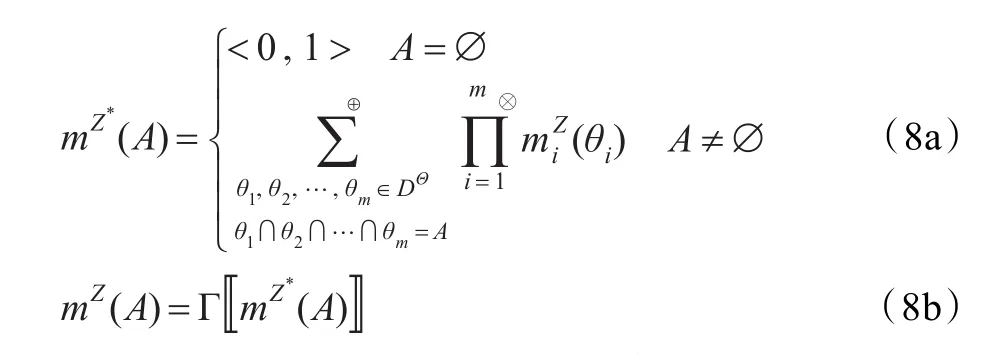
这里给出Γ〚·〛的一种简单形式：∀i=1，2，…，n

将DSmT在直觉模糊集上拓展之后，所有运算都变成了直觉模糊数之间的运算。根据直觉模糊DSm组合规则得到的焦元组合直觉模糊信度赋值仍是一个直觉模糊数。在得到所有焦元经证据组合后的直觉模糊信度赋值之后，就可以对它们根据相应直觉模糊信度赋值的大小进行排序，并做出最优决策。为比较直觉模糊信度赋值的大小，在此给出如下定义：

定义2设θ1，θ2∈DΘ，相应的直觉模糊信度赋值为：mZ(θ1)=＜μz(θ1)，νz(θ1)＞，mZ(θ2)=＜μz(θ2)，νz(θ2)＞，若满足下列条件之一，则有mZ(θ1)＜mZ(θ2)：

（1）μz(θ1)-νz(θ1)＜μz(θ2)-νz(θ2)

（2）μz(θ1)-νz(θ1)=μz(θ2)-νz(θ2)且 μz(θ1)+νz(θ1)＜μz(θ2)+νz(θ2)

4 数值仿真及分析

雷达和红外是两种常用的探测设备。在实验系统中分别采用这两种设备对仿真目标进行识别。设定的仿真目标包括战区战略导弹TBM（T），歼击机（J）以及诱饵（B），因此鉴别框为Θ={T，J，B}，采用自由DSm模型，即允许鉴别框Θ中的元素存在交集。关于探测设备对仿真目标的探测识别机理以及内部数据的处理过程，本文暂不讨论，直接给出各传感器对目标的识别报告，具体数据如表3所示。

表3 目标识别的广义基本信度赋值分配

表4 目标识别的直觉模糊信度赋值分配

表5 目标识别的证据组合结果对比

步骤1构造初始的各焦元的直觉模糊信度赋值分配（IFS_bba）

构造方法如下：

（1）分别计算每个传感器证据对各命题余集的广义信度函数值；

（2）构造对应于各命题θi的直觉模糊信度赋值＜mj(θi)，＞。

步骤1的执行结果如表4所示。

步骤2对各传感器的证据数进行组合

为方便进行比较分析，本例同时还运用了经典的DSm组合规则和K-DSm组合规则来对证据进行组合。采用各种组合规则得到的结果如表5所示。

步骤3决策分析

决策的方法是选取直觉模糊信度赋值最大的焦元作为最终的目标识别结果。

根据定义2，对表5中的直觉模糊信度赋值进行大小排序，很容易得到mZ(T)=＜0.484 4，0.013＞是其中最大的直觉模糊数，即焦元T的直觉模糊信度赋值最大，从而判定目标最有可能为TBM，显然，这与基于DSm组合规则和K-DSm组合规则的识别结果是一致的。

在定义直觉模糊信度赋值时，将其中的肯定信任度等价于DSm模型下的广义基本信度赋值。由于直觉模糊信度赋值更全面地描述了证据源提供的信息，在直觉模糊拓展DSm组合规则的证据组合过程中，有效发挥了直觉模糊信度赋值的优势，焦元的肯定信任度和否定信任度的合成值能够相互修正，使得组合结构更为准确和合理。从表5中可以发现，虽然根据三种组合规则，得出的结论一致，都是判定目标为TBM的可能性最大，但是它们包含的不确定性程度是存在差别的。在决策过程中，信度赋值分配越集中，则越有利于最优决策，即信息包含的不确定性越少。从组合结果来看，焦元T的直觉模糊信度赋值中的肯定信任度为0.484 4，大于经典DSm组合规则和K-DSm组合规则组合结果中焦元T的基本信度赋值，同时，焦元T的否定信任度很小，因此，相比其他两种合成结果，基于直觉模糊拓展DSm组合规则的组合结果的决策具有最小的决策风险，从而为决策过程提供更可靠的支持。

需要指出，由于直觉模糊信度赋值包含了更多的信息，其所需要的存储空间是基本信度赋值的两倍；直觉模糊拓展DSm组合规则相比经典DSm和K-DSm组合规则的计算复杂度也更高，因此采用该规则需要付出的代价更高。但是从证据合成结果的合理性和准确性的角度来考虑，直觉模糊拓展DSm组合规则仍不失为一种有效的选择。进一步研究和完善DSmT在直觉模糊集上的拓展方法和过程具有较高的理论和应用价值。

5 结语

本文的内容主要分为两部分。第一部分从一个简单的例子出发，指出DSmT的组合结果通常不能有效地减少信息的不确定性，并且存在计算复杂度高的问题，针对DSmT存在的缺陷，提出了一种新的基于冲突再分配的证据组合规则，即K-DSm组合规则，该规则在组合结果中清除了冲突焦元，并将冲突焦元的信度同时分配给了引起冲突的主焦元和完全的未知集，使得信度的分配更为合理；第二部分研究了DSmT在直觉模糊集上的拓展，将直觉模糊集在描述和处理模糊信息等方面的优势引入到DSmT中，进一步增强了DSmT组合冲突、模糊和不精确证据信息的能力。本文为DSmT理论的完善和改进提供了两种新的思路，但还不够成熟，仿真结果初步验证了这两种思路的价值。

[1]潘泉.信息融合理论的基本方法与进展（II）[J].控制理论与应用，2012，29（10）：1233-1244.

[2]段新生.证据理论与决策、人工智能[M].北京：中国人民大学出版社，1993.

[3]韩德强.基于证据距离与不确定度的证据组合方法[J].红外与毫米波学报，2011，30（5）：396-400.

[4]Yamada K.A new combination of evidence based on compromise[J].Fuzzy Sets and System，2008，159（13）：1689-1708.

[5]Smarandache F，Dezert J.Advances and applications of DSmT for information fusion，vol.1[M].Rehoboth，USA：American Research Press，2004.

[6]曲圣杰.冲突再分配DSmT及解决证据间矛盾的新方法[J].控制与决策，2009，24（12）：1856-1860.

[7]Li X，Dezert J，Smarandache F，et al.Evidence supporting measure of similarity for reducing the complexity in information fusion[J].Information Sciences，2011，181（10）：1818-1835.

[8]陈凯，杨俊安，陈昊.DSmT混合规则高复杂度优化[J].计算机工程，2010，36（7）：76-79.

[9]李新德.一种快速分层递阶DSmT近似推理融合方法（B）[J].电子学报，2011，39（3A）：31-36.

[10]胡丽芳，关欣，何友.一种新的基于DSmT的合成公式[J].火力与指挥控制，2009，34（7）：9-11.

[11]李鹏，黄心汉，王敏.DSmT框架下的自适应通用分配法则[J].计算机工程与应用，2010，46（6）：16-19.

[12]Yager R.On the Dempster-Shafer framework and new combination rules[J].Information Sciences，1987，41（2）：93-138.

[13]Dubois D，Prade H.Representation and combination of uncertainty with belief functions and possibility measures[J].Computational Intelligence，1998，4（3）：244-264.

[14]徐泽水.直觉模糊信息集成理论与应用[M].北京：科学出版社，2008.

TANG Changchun,AO Zhigang,GONG Yunxiang,ZHANG Kangyi,WANG Youcheng

College of Field Engineering,PLA University of Science and Technology,Nanjing 210007,China

Dezert-Smaradache Theory retains conflicting focal element in the combined result,which benefits the combination ability for conflict evidence,meanwhile,it results in the accumulation of conflicting information,and makes the composite reliability of main focal element reduce illogically.A new combination rule based on conflict redistribution is proposed to resolve the problem of DSmT.In order to further improve the DSmT performance in dealing with uncertain, highly conflicting and imprecise information,this paper researches the method to develop DSmT on the intuitionistic fuzzy sets.An intuitionistic fuzzy belief assignment mapping is defined to replace traditional belief assignment function, and the combination rule based on the new mapping is discussed in this paper.Numerical examples demonstrate the effectiveness of the proposed method.

information fusion;DSmT;conflict redistribution;intuitionistic fuzzy sets

DSmT在组合结果中保留了冲突焦元，一方面提高了组合冲突证据能力，另一方面造成了冲突信息的积累，促使分配给主焦元的信度不合理地减小，导致组合信息的不确定性增加，不利于决策。针对DSmT存在的缺陷，提出了一种新的基于冲突再分配的组合规则。为进一步提高DSmT处理冲突、模糊和不精确信息能力，研究了DSmT在直觉模糊集上的拓展，将传统的信度赋值函数替换为直觉模糊信度赋值映射，并讨论了直觉模糊拓展后的信度组合规则。数值实例验证了所提方法的有效性。

信息融合；DSmT；冲突再分配；直觉模糊集

A

TP391

10.3778/j.issn.1002-8331.1212-0385

TANG Changchun,AO Zhigang,GONG Yunxiang,et al.Improvement of DSm combination rule and its development on intuitionistic fuzzy sets.Computer Engineering and Applications,2014,50（24）：151-155.

江苏省自然科学基金（No.SBK2009061）。

唐长春（1986—），男，硕士研究生，CCF会员，研究方向：信息融合，军用数据及知识工程；敖志刚（1959—），男，教授，研究方向：指挥自动化与战场环境数字化，万兆以太网；张康益（1988—），男，硕士研究生，研究方向：联合作战演练系统分析与集成；王有成（1985—），男，硕士研究生，研究方向：指挥自动化与战场环境数字化。E-mail：357502975@qq.com

2013-01-04

2013-03-25

1002-8331（2014）24-0151-05

CNKI网络优先出版：2013-04-09，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130409.1522.002.html

◎图形图像处理◎