基于复合混沌系统的多小波鲁棒水印算法

曲长波，杨晓陶，史双宇

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

基于复合混沌系统的多小波鲁棒水印算法

曲长波，杨晓陶，史双宇

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

1 引言

数字水印（digital watermarking）最早在1993年由Tirkel等人提出，和数字加密技术一起成为信息安全领域的两个重要分支。基于图像的数字水印技术和图像加密技术是近年来信息安全领域的研究热点。数字水印主要性能包括不可见性、鲁棒性和安全性等。

按嵌入到载体中位置的不同可以分为时域水印和变换域水印。时域水印是直接在载体中嵌入水印信息。时域算法简单有效，嵌入容量大，但是往往鲁棒性较差。变换域水印算法一般在特定的变换域嵌入水印，例如：离散余弦变换（DCT）[1]，离散小波变换（DWT）[2-5]和离散多小波变换（DMWT）[6-7]。文献[2]提出了一种基于DWT和SVD（奇异值分解）的数字水印算法，得到了很好的效果。该算法只使用了Arnold变换对图像进行一般置乱，无法保证系统的安全性，同时在JPEG压缩之后算法的PSNR值会有很大程度的下降。李峰、陈光喜等人[3]引入混沌置乱和HVS（人眼识别系统），有效增加了算法对JPEG压缩的抵抗，但是其置乱方法非常简单，所得结果面对噪声干扰效果不佳。文献[4]在此基础之上，详细地讨论了关于混沌系统应用于图像置乱加密的方法，并提出了一种行之有效的评价标准。叶天语[5]提出了一种DWT-SVD域的全盲鲁棒水印算法。该算法引入自嵌入技术，可以全盲并且准确地得到水印图像，但是由于其嵌入水印与图像自身相关，一旦受到较大幅度的干扰或者是攻击时，算法的鲁棒性能就会急剧下降，尤其是剪切攻击和噪声干扰。为了解决DWT-SVD算法鲁棒性问题，谢小贤[6]考虑到多小波变换能更好地获得子图相关性，提出了基于 GHM多小波变换域上的自适应水印算法，取得了很好的实验结果。文献[7]使用平衡多小波代替GHM多小波，算法显著提高了系统的鲁棒性。

本文引入复合混沌系统，在文献[5，7]基础之上，提出一种基于复合混沌系统的图像置乱加密算法，同时提出一种平衡多小波与SVD相结合的鲁棒水印算法。通过不可见性，加噪、压缩等图像处理和几何攻击等鲁棒性实验的结果进行分析对比，得出该算法有很好的鲁棒性。

2 相关基础理论

2.1 复合混沌系统

混沌（Chaos）是一种复杂的非线性过程，是指某些非线性系统具有非常强的初值敏感性，从而系统中出现了一种内在的随机性[8]。二维Logistic映射模型：

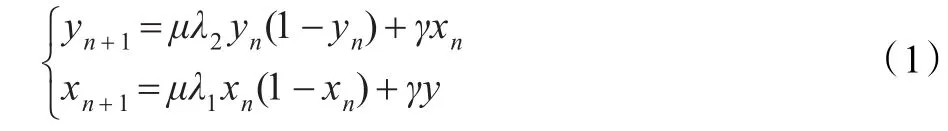
其动力学行为是由控制参数 μ、λ1、λ2和γ决定的。当 μ=4，γ=0.1时，在参数λ1=λ2=0.89时，系统出现混沌现象[9]。

一维4分段线性混沌映射的定义为：

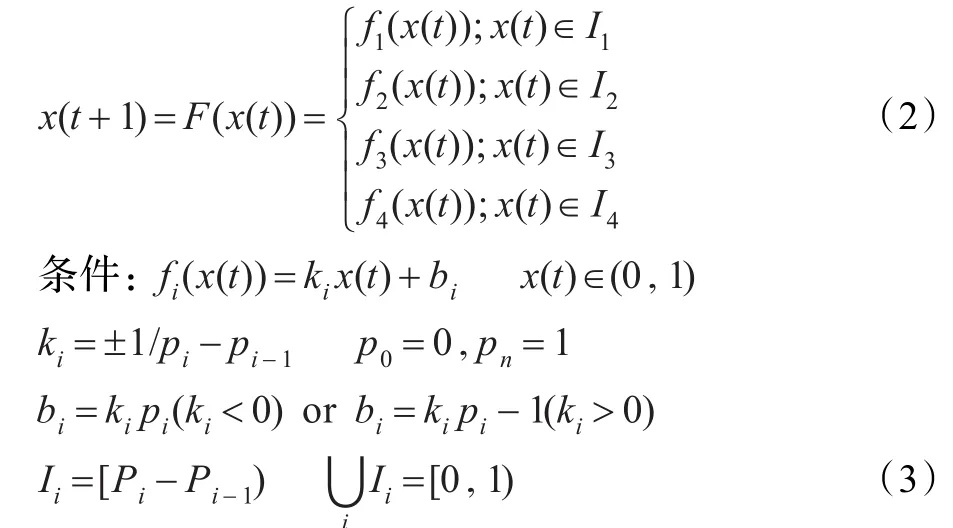
其中i∈{1，2，3，4}，n=4。

可以证明（1）该迭代系统是混沌的；（2）其输出信号在[0，1)上遍历。

证明：（1）系统的Lyapunov指数λ为：

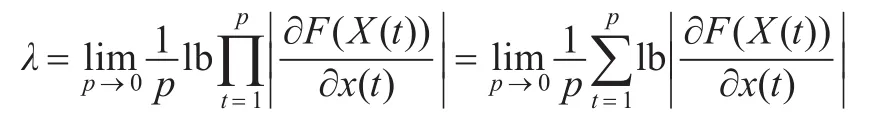
由条件式（3）可知：|∂F(x(t))/∂x(t)|＞1。所以λ＞0可知系统是混沌的。

（2）根据条件式（3）可以计算Frobenius-perron算子：

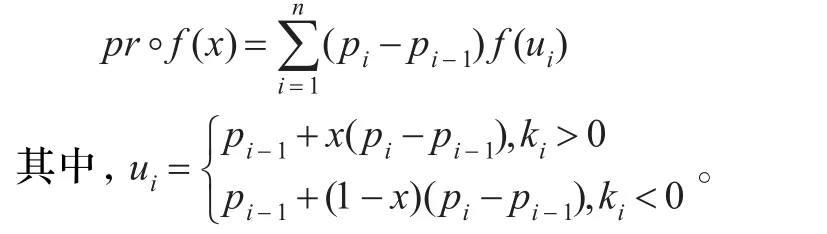
得到 f(x)=pr◦f(x)的唯一解是 f(x)=1。所以（2）得证。

2.2 多小波与平衡多小波

多小波变换是在小波变换构架的基础之上提出的新概念，但是却有着很多重要的区别。多小波的基本思想是将单小波中由单个尺度函数生成的多分辨率分析空间扩展为多个尺度函数生成，以此来获得更大的自由度。

若一个多分辨分析是由多个尺度函数生成，相应的由多个小波函数平移与伸缩构成L2(IR)空间的基，那么这些小波函数被称作多小波。

在对图像进行多小波处理的时候，由于多小波的低（高）滤波器都是矩阵形式，不能直接参与卷积运算，因此必须对输入信号进行预处理。然而预处理的过程很有可能会破坏多小波的一些基本特性，而平衡多小波则可以避免这样的问题。定义与多小波低通滤波器相对应的Toeplitz矩阵为：

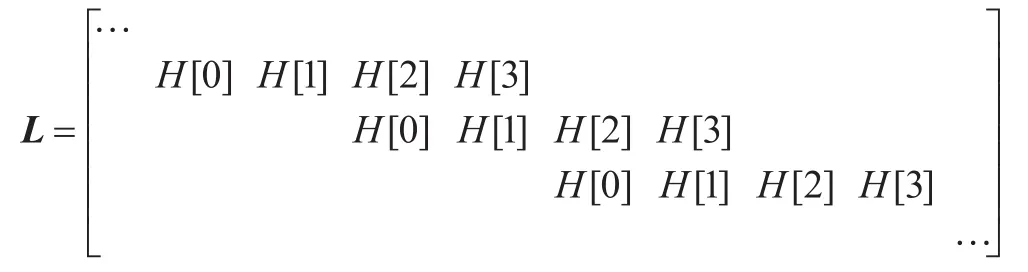
如果LTu1=u1，u1=[…，1，1，1，1，…]，则称系统是平衡多小波。Cardbal2多小波是平衡多小波的一种，图像经过Cardbal2多小波变换之后，其低频能量并不是像GHM多小波那样将能量按照4.5∶2.2∶2.2∶1的比例分配；也不是像CL小波那样把能量的97%都集中在左上角的块中；它是将能量几乎平衡地分配到每个字块。其数值大小相当，能量均匀，表示出很强的关联性[9]。GHM变换、cardbal2变换效果如图1所示。

图1 多小波变换效果对比图

2.3 奇异值分解

奇异值分解是一个矩阵对角化的数值方法。关于奇异值分解的定义[3]如下：

设A∈Rm×n，则∃U∈um，V∈vn，使得：

其中：Σr=diag(λ1,λ2,…,λr)∈Arr，并且 λ1≥λ2≥…≥λr＞0，um表示m×m的矩阵。式（4）称之为A的奇异值分解。令S=[Σr，0;0，0]，则S=UAVT，S称之为 A的奇异值矩阵。

本文使用SVD的主要原因：（1）奇异值对应于图像的能量特性（亮度特性），而非纹理特性；（2）奇异值所表现的是图像的内蕴特性，反映的是图像矩阵元素之间的统计关系；（3）所以说奇异值具有相当好的稳定性，当图像受到修改或攻击时，它的奇异值不会发生大的变化；（4）矩阵奇异值分解得到的奇异值中，第一个奇异值要比其他的奇异值大得多。

3 水印嵌入与提取算法

3.1 水印复合混沌置乱加密

对于复合混沌系统的置乱加密，文献[10]的4分段线性混沌映射的系数选取为：p0=0，p1=t，p2=0.5，p3=1-t，p4=1。其中t∈(0，0.5)。文献[10]算法将2维Logistic映射所产生的一条混沌序列{y}/2赋值给{t}（{·}表示序列）。但是这样做使得{t}的赋值异常简单，也没有充分发挥2维Logistic映射的优势，其效果和使用一维Logistic映射效果相差不大。

本文改进方法：使用2维Logistic映射所产生的两条混沌序列，经处理后作为一维4分段线性混沌映射系数 pi的输入值。对于尺寸为m的水印，选择初值(x0，y0)带入2维Logistic映射生成的混沌序列{xj}、{yj}，j∈{1，2，…， m×m}。令 p0=0，p1j=xj，p2j=(xj+yj)/2，p3j=yj，p4j=1，ki=1/pi-pi-1，i∈{0，1，2，3，4}。这样既充分利用到生成的2条混沌序列又增加了系数选取的复杂性，也就保证了加密的安全性。

水印置乱加密具体过程如下：

（1）选取参数μ=4，γ=0.1，λ1=λ2=0.89和初始值(x0，y0)，代入2维Logistic混沌映射公式（1）中，生成两个长度为m×m混沌序列{xj}，{yj}，j∈{1，2，…， m×m}。

（2）将生成的xj、yj作为线性混沌映射的系数同时选择线性混沌系统的初始值x(t)0=l，满足：p0j=0，pij= xj，p2j=(xj+yj)/2，p3j=yj，p4j=1，ki=1/pij-p(i-1)j，i∈{0，1，2，3，4}，j∈{1，2，…， m×m}。经系统生成一条混沌序列x(t)j，j∈{1，2，…， m×m}。

（4）将二值水印图像W扫描成一维行向量，与二值化算子进行异或，得到秘密水印W0。

原始水印与置乱加密后水印对比如图2所示。

图2 置乱对比

解密算法与加密算法类似，先使用保存的密钥按照步骤（1）～（3）生成二值化算子，将秘密水印和算子进行异或，得到水印信号。

3.2 水印嵌入算法

本文算法的基本思想是：采用二值图像作为水印信号，首先对水印图像通过复合混沌系统进行混沌加密，去除水印图像的自相关性，使其表现出类随机性分布。同时对载体图像进行cardbal2平衡多小波变换，然后对低频子带中的4个部分(LL2，HL2，LH2，HH2)分别按4×4分块，对各个子块进行奇异值分解得到块最大特征值序列分别是{ai}、{bi}、{ci}、{di}，选取HH2子块最大特征值{di}作为嵌入点进行嵌入。

本文算法具体嵌入方法如下：

步骤1水印信号通过复合混沌系统进行置乱加密，并保留密钥。

步骤2对载体图像I进行cardbal2多小波变换，得到4个低频子带和3个中高频子带，如图3所示。

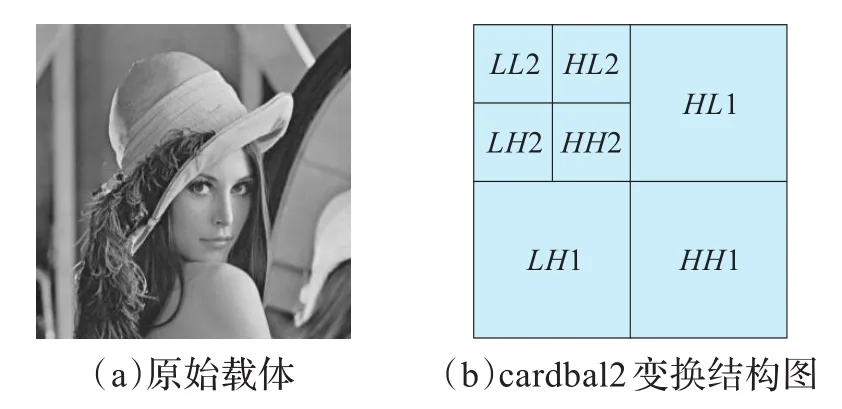
图3 cardbal2变换结构

步骤3对生成的4个低频子带——LL2，HL2，LH2，HH2，分别按照4×4分块；并对各个子块进行奇异值分解得到块最大特征值序列分别是{ai}、{bi}、{ci}、{di}。

步骤4计算均衡因子 X={xi|xi=(ai+bi+ci)/3}按照如下规则进行嵌入：

得到新的特征值序列{di*}。其中 β是嵌入强度系数，由用户自己定义。

步骤5分别对{ai}、{bi}、{ci}、{di*}进行奇异值重构，得到多小波低频子带，再做cardbal2逆变换得到含水印图像I′。

3.3 水印提取算法

水印的提取过程是嵌入算法的逆过程，设I′是经过攻击后的待检测图像。提取过程如下：

步骤1对含水印图像I′进行cardbal2多小波变换，得到4个低频子带和3个中高频子带。

步骤2对生成的4个低频子带——LL2，HL2，LH2，HH2，分别按照4×4分块；并对各个子块进行奇异值分解得到块最大特征值序列分别是{a*i}、{b*i}、{c*i}、{di*}。

步骤3和嵌入算法一样，先要计算均衡因子 X*= {x*i|x*i=(a*i+b*i+c*i)/3}，并计算均衡因子和{di*}之间的差值θ={θi|θi=di-x*i}。按照如下规则提取：

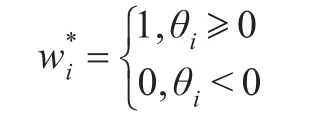
得到待解密水印W0*。

步骤4使用加密时的密钥生成特定的复合混沌系统，将W0*带入复合混沌系统解密，得到水印信号W*。

4 实验结果及其分析

4.1 实验参数说明

本文实验选用32×32“版权保护”二值水印，载体选用512×512×8，256灰度Lena标准图像。本文算法中复合混沌置乱加密系统的初始值为：(x0，y0)=(0.1，0.11)，p=4，密钥l=0.247。嵌入算法中的参数β=3。

混沌系统的初值选择原则：(x0，y0)的选择要满足2维Logistic映射的混沌条件。但是考虑到2维Logistic映射靠前的数值往往存在不稳定的情况，本文实验舍去前L=1 000个数据，L也可以作为密钥保存，这样无形中加大了系统的密钥空间。 p的选取主要是按照混沌序列的计算精度，本文实验环境为Matlab7.0，实验精度为4位，所以 p=4，l为满足l∈(0，1)随机选取。

数字水印的不可见性评价又称为透明性评价。嵌入水印后载体图像的客观评价指标主要是PSNR（峰值信噪比）[11]。

由图5(a)可知，当min{intervali} 和S一定时，asp随n的增大而减小，表明可通过增加入侵者在单条入侵路径上所必须顺序攻击的脆弱性数量来提高动态防御有效性.

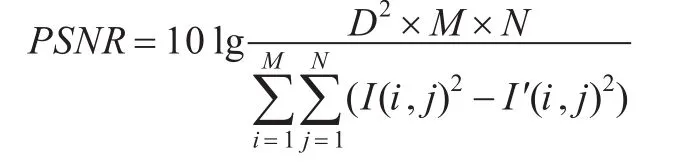
其中I表示原始图像，I′表示嵌入之后的图像。D表示信号可能取的最大值，对一个8位图像来说，每个像素值的峰值就是255。PSNR的单位是分贝（dB）。

根据统计经验一般PSNR值在38以上，人眼是不能看出原始图像和含水印图像之间的差别的。经过实验，本文算法PSNR为42.248，和文献[7]的36.668相比有明显提高，与文献[5]的41.483相比基本上达到了同样的效果，都无法用肉眼识别。原始载体图像和嵌入水印后的载体图像对比如图4所示。

数字水印的鲁棒性是衡量数字水印好坏的重要指标之一。本文采用定量地刻画鲁棒性——归一化相关系数（NC）[12]来衡量。

图4 嵌入前后载体对比

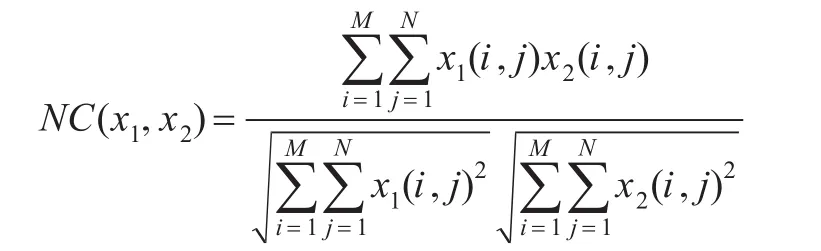
其中x1，x2分别表示初始水印和提取的水印。原始水印、本文算法所得到的水印对比如图5所示。

图5 无干扰条件下提取水印对比

依照本文的算法，在无干扰的情况下提取的水印NC值达到1。文献[7]算法NC值也为1，文献[5]由于算法自身的限制为0.998 3。

4.2 抗攻击鲁棒性实验

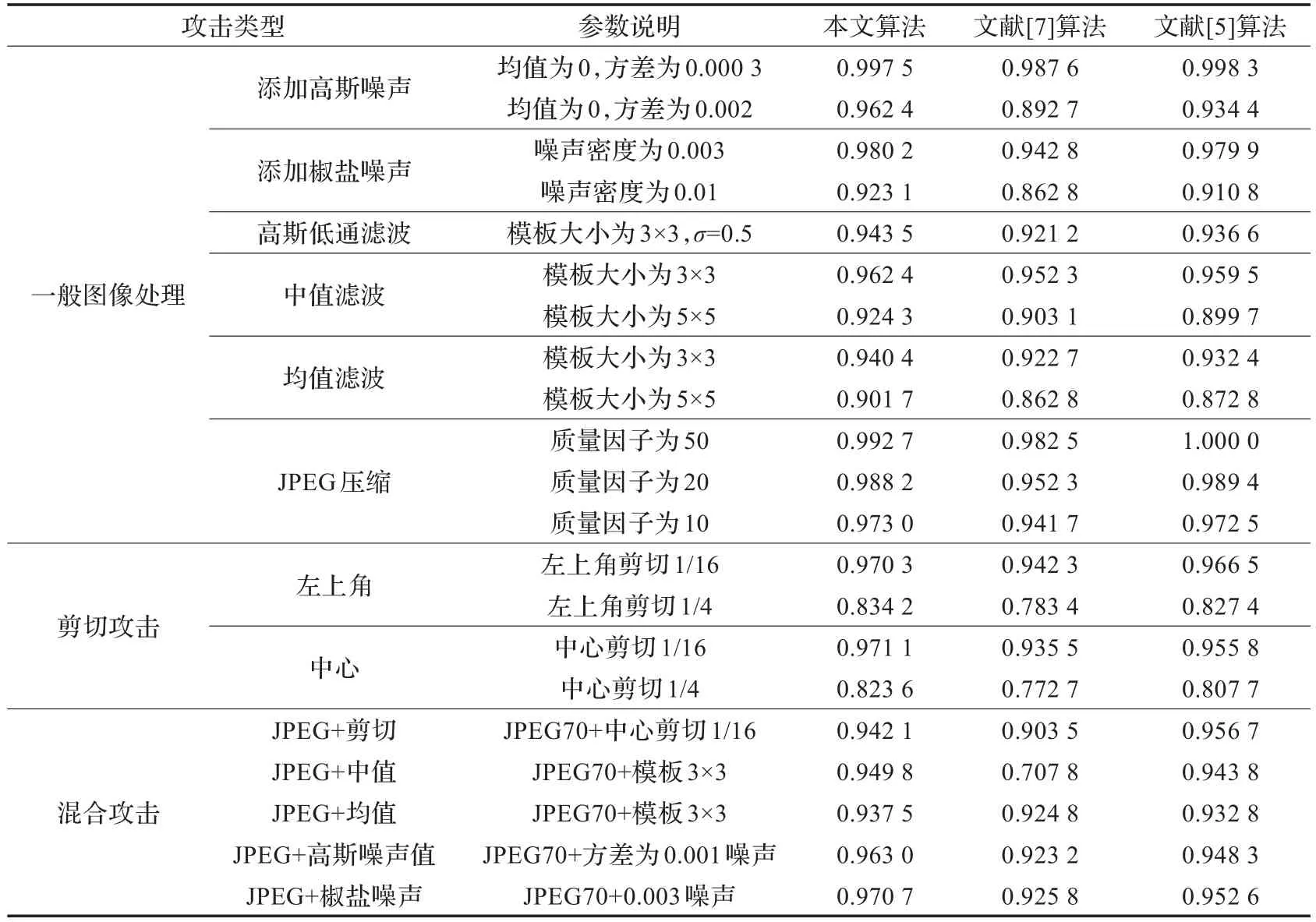
表1 抗攻击鲁棒性实验性能对照表

4.3 实验结果分析

（1）鲁棒性分析

通过表1可以清晰看出，本文算法无论是对一般图像处理还是剪切攻击都具有一定的鲁棒性，主要是由于复合混沌置乱加密算法有很好的置乱效果，基于cardbal2多小波和SVD算法对于外界“扰动”不敏感，这正是本文算法有较强鲁棒性的原因。

（2）算法参数β的选取

参数β的选取决定了本文算法不可见性和鲁棒性，β取值越小不可见性越好，β取值越大鲁棒性越好。因此 β的取值其实就是在不可见性和鲁棒性之间的折中，本文将不可见性控制在42左右，在保证人眼不能直接观察出图像是否经过修改的前提下，尽可能加强算法的鲁棒性。但是载体图像的差异使得 β的取值很难用一个具体的公式统一确定，但是应该保证 β≤min(|xi-di|/2)。通过表1可以看出β=3是比较适合的。

（3）与文献[5，7]鲁棒性比较分析

通过表1，可以发现文献[7]由于使用简单的置乱系统，置乱效果不是很理想，同时没有引入SVD而是直接修改亮度值，使得算法本身对外界干扰抵抗性不足。文献[5]在鲁棒攻击较弱时，表现出了非常良好的鲁棒性，但是由于算法本身要求生成的水印和载体图像之间有很强的相关性，导致在攻击逐渐加大时，算法鲁棒性下降很快。

5 结束语

本文利用复合混沌系统对水印进行置乱加密，取得了较好的测试效果和良好的视觉效果。本文在文献[5]和文献[7]的基础之上，引入cardbal2多小波和SVD变换相结合的嵌入算法。通过实验表明，可以看出本文算法有良好的不可见性同时对一般图像处理和剪切攻击、混合攻击有很好的鲁棒性。

[1]肖俊，王颖.基于多级离散余弦变换的鲁棒数字水印算法[J].计算机学报，2009，32（5）：1055-1061.

[2]周鹏颖，沈磊，田小林，等.基于小波—奇异值分解的数字水印新算法[J].计算机应用研究，2010，27（5）：1896-1897.

[3]李峰，陈光喜.基于混沌和HVS的小波域自适应图像水印算法[J].计算机应用研究，2012，29（6）：2225-2227.

[4]薛胜男，陈秀宏.基于混沌加密和SVD的数字图像水印算法[J].计算机工程，2012，38（19）：108-110.

[5]叶天语.DWT—SVD域全盲自嵌入鲁棒量化水印算法[J].中国图象图形学报，2012，17（6）：644-650.

[6]谢小贤.基于GHM和FCM的自适应图像水印算法[J].计算机工程与应用，2008，44（12）：204-206.

[7]胡社教，谢锦生.基于平衡多小波与神经网络的图像水印算法研究[J].系统仿真学报，2008，20（11）：2995-2998.

[8]段文文，李碧.基于混沌的数字图像置乱算法及参数优化[J].计算机应用研究，2011，28（1）：329-331.

[9]黄卓君，马争鸣.多小波变换的统计分析[J].中国图象图形学报：A版，2001，6（12）：1198-1203.

[10]王丽燕，李永华.一种基于复合混沌动力系统的序列密码算法[J].大连理工学报，2012，52（5）：731-735.

[11]Arnold M.Attack on digital audio watermarks and countermeasures[C]//Proceedings of Third International Conference on Web Delivering of Music，2003：55-62.

[12]Wang C C.Repeating image watermarking technique by the visual cryptography[J].IEICE Transactions on Fundamentals，2000，36（13）：1108-1110.

[13]刘志刚，黄慧汇.基于不同预处理方法的多小波暂态信号去噪[J].电子学报，2004，22（6）：1054-1056.

QU Changbo,YANG Xiaotao,SHI Shuangyu

Software College,Liaoning Technical University,Huludao,Liaoning 125105,China

This paper puts forward a kind of robust watermarking algorithm based on block SVD,the hybrid system and balanced multiwavelet.To being embedded watermarking signal,it should make hybrid chaotic system to be scrambled and encrypted.Then the coverimage should be changed by cardbal2 multiwavelet.Low frequency sub-band is done 4×4 blocks,SVD handling and embedded according to embedded coefficients and equilibrium factor.The experimental results show that this algorithm has good invisibility and robustness.

hybrid chaotic;blocks singular value decomposition;balance multiwavelets;equilibrium factor;robust watermarking

提出了一种基于复合混沌系统与平衡多小波、块SVD相结合的鲁棒水印算法。对待嵌入水印信号进行复合混沌置乱加密；对载体图像作一次cardbal2多小波变换；对低频子带进行4×4分块并做SVD处理，根据均衡因子和嵌入系数进行嵌入。实验结果表明算法有很好的不可见性和鲁棒性。

复合混沌；块奇异值分解；平衡多小波；均衡因子；鲁棒水印

A

TP393

10.3778/j.issn.1002-8331.1301-0303

QU Changbo,YANG Xiaotao,SHI Shuangyu.Robust watermarking algorithm based on hybrid chaotic system and multiwavelet.Computer Engineering and Applications,2014,50（24）：91-95.

曲长波（1963—），男，高级工程师，研究领域为图像处理，信息隐藏；杨晓陶（1989—），男，硕士研究生，研究领域为图像处理，信息隐藏；史双宇（1988—），男，硕士研究生，研究领域为信息隐藏。E-mail：marshall121@163.com

2013-01-28

2013-03-15

1002-8331（2014）24-0091-05

CNKI网络优先出版：2013-04-08，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130408.1646.002.html