主动端到端离散式时延分布估计方法研究

吴辰文，李培儒，茹俊年，刘香丽

兰州交通大学 电子与信息工程学院，兰州 730070

主动端到端离散式时延分布估计方法研究

吴辰文，李培儒，茹俊年，刘香丽

兰州交通大学 电子与信息工程学院，兰州 730070

随着网络信息化的快速发展，网络性能测量逐渐成为一个重要的研究领域。而传统的网络测量方法受到安全因素的制约，只能测量权限范围内的网络性能，因而一些研究者提出了一种新的网络性能测量方法——网络断层扫描技术[1-3]，即NT技术（Network Tomography）。网络断层扫描技术是通过主动发送多播探测包获得潜在的链路信息，应用统计推断的方法获得网络的时延、丢包率和拓扑结构等性能，已逐渐成为近年来网络性能评价研究的热点。

网络性能测量中，时延性能检测是网络断层扫描技术的一个重要研究内容。目前的估计方法主要是基于连续时延模式[4]。国际国内相关机构不断研究新的测量、估计方法，但是直接测量始终存在算法复杂度问题难以解决。在实际的测量过程中，大量网络边缘客户接入点的计算量无法控制。从而导致连续时延模式估计算法无法适应大规模网络。

离散时延模式估计时延分布最早于2002年由Presti[5]等人提出，使用递归法估计时延分布情况。它并不是一般的最大似然估计MLE（Maximum Likelihood Estimator）问题，因为受到网络规模等因素的限制，无法直接进行计算。此后Liang和Yu提出了伪似然估计算法[6]，即MPLE算法（Maximum Pseudo Likelihood Estimation），它将路由矩阵划分成数个区域，相比于原有的EM算法减小了计算的复杂度，但是针对不同的网络拓扑矩阵如何划分，划分后如何合并的问题仍难以找到有效的解决方法。本文不使用单纯的单播或者多播实验，而描述一种较为灵活的组播探测实验，将网络拓扑划分成多个子树，先后从广度和深度两个步骤研究链路时延的估计算法，探究最大似然估计问题的更快、更有效的解决方法。

1 离散时延估计原理

1.1 模型定义

网络时延分布估计是将网络抽象成树状逻辑网络模型，即一个有向无环树。用T=(V，E)来表示一棵树，V表示节点集合，E表示链路集合。节点、链路遵循规范的编号方式，节点0表示根节点，所有链路用其末端节点所命名，如链路1表示节点0和节点1所链接的链路。 f(k)表示节点k∈V的父节点。在一棵树中，除根节点0以外其余所有节点有唯一的父节点。递归定义fi(k)=f{fi−1(k)}，其中 f1(k)=f(k)。如果节点k在树的L层上，则有 fL(k)=0。定义D(k)表示为节点k的子节点集合，集合中所有节点的父节点是节点k。用R表示叶子节点集合，即没有子节点的集合。最后要说明一个概念，内部节点是既拥有父节点，又拥有子节点的节点。如图1所示，用一个简单树形结构展示以上定义的概念。

网络断层扫描技术的时延分布推断是一个大规模的逆概率估计问题。如图1所示，可以使用9元的端到端的测量数据估计15条链路的时延分布情况，将构成非满序矩阵，无法求出时延分布的结果。而此9元测量数据之间的依赖关系则是解决问题的关键，通过对这种相互依赖关系的进一步分析和挖掘，能够为有效解决路径时延到链路级信息的逆问题提供可行性途径。因此，首先考虑使用最大似然估计算法MLE。

1.2 时延离散化

网络时延状况呈现随机分布，但是可以将网络中的时延简单地看作好与差两种状态。探测包的时延保持在τ值以下时，网络状况被视为好；当时延超过τ值，则网络变得拥塞，网络状况被视为差，如图2所示。

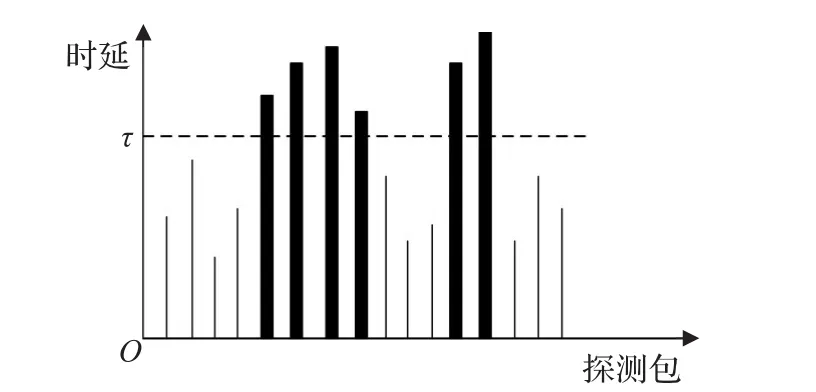
图2 网络时延状况

然后，设定一个离散化的量化宽度值bin，根据bin尺寸的大小将时延τ进行等长划分[7]，如图3所示。因此从根节点到叶子节点路径上的时延Yr便可用离散数据来表示，其取值范围为{0，q，2q，…，bq}，其中q是量化宽度bin的大小，b是最大离散时延值，q和b将用于所有链路Xk。本文将忽略丢失和差状况下的时延数据。

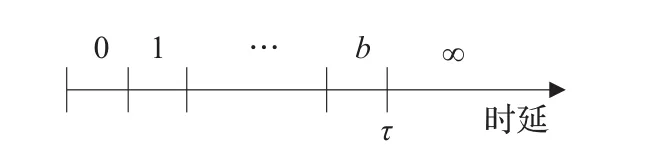
图3 时延离散化

虽然这个框架的设置看上去似乎很苛刻、死板，限制条件众多，但是在实际应用中却不失其实用性。首先，根据实际的网络流量数据显示，网络流量往往异于某一种或者几种特定的网络，如将网络流量假设成泊松分布[8]并不能代表真实的网络状况，所以选择一种特定的参数模型概括所有链路时延分布是非常困难的，实用性也并不强。其次，时延数据通常具有突发性的特点，在这种情况下末端分布是相当有用的。离散模型对于首部共享链路过多的链路无法做任何假设，而通过发送足够数量的探测包可估计末端分布估计。bin的大小可以通过收集来的数据做出相应的调整，bin值较小时可以用来估计详细信息分布；bin值较大时可用于获取长尾信息。

定义P0，r为从节点0到节点r的路径，路径P0，r测得网络时延是其经过的各条链路时延累计的结果：

Y为测量所得路径时延向量，X为链路时延向量，A为链路矩阵。例如，图1中Y3=X1+X3。用αk(i)来表示链路k上时延等于iq的概率，即αk(i)=P(Xk=iq)，i=0，1，…，b。目的是用Yr的测量结果来估计一系列链路的时延分布情况，其中k∈E，i∈{0，1，…，b}。因此，αk= [αk(0)，αk(1)，…，αk(b)]为链路不同时延值概率向量，α= [α′0，α′1，…，α′|E|]′为各条链路的不同时延值的概率矩阵。用αu，v(i)来表示路径Pu，v上的累计时延等于i的概率。

本文假设时延是时间独立的，即在一段链路上的时延独立于在另一段链路上的时延。只要发送的探测包之间的时间间隔足够大，时间独立的假设就是合理的。只要测试时间足够短，对网络情况不构成重大改变，时间稳定性也是合理的。

2 时延分布估计算法

2.1 组播发包策略

多播探测实验易于实施，但它却有计算量较大，难于计算的缺点。而单纯的单播探测实验很难将接收节点之间的相关性联系起来，基于此原因使用组合单播探测包的方法可以改善这一不足，比如背靠背、三明治列车等组合单播策略[3]。而文中将会使用更加灵活的组播端到端测量[9-10]方法，该方法发送不同的探测包到不同的网络区域，将网络划分成不同的子树，探测包发送的强度不同可以取决于网络服务质量的不同。同时这种较为灵活的发包方法不同于以往依赖拓扑或者参数分布状况，它可以通过无参估计所有链路的时延分布情况。在实践中，选择的特定组播实验将取决于不同的实际考虑。事实上可以改变组合方式，随着时间的推移探索不同区域，不同强度取决于阻塞或其他可能出现的问题。其中对播策略是效率最高的，对播组将探测包经过的路径划分成两层三链子树，将MLE问题规模始终控制为最佳。另一方面，相比多播实验，对播策略使得探测包在网络中的传输不影响网络的负载状况。因此，文中将以多对播策略作为主要研究手段。

每一种发包策略将从根节点0出发，而且接收节点必须覆盖所有叶子节点。

定义1把从一个接收节点到k个指定接收节点的发包方式定义为k播组。

例如对1.1节中的图1所示的逻辑网络模型树状图来说，假设定义＜2，12＞是一个对播（或2播）组，则＜8，9，13，14，15＞是一个5播组，其余的将分为一组，从而形成一个发包策略C，可表示为C={＜2，12＞，＜8，9，13，14，15＞，＜10，11＞}。而制定一个发包策略需要符合如下两个条件：

（1）对于每一内部节点s∈T{0，R}属于至少一个k播组，k＞1。

（2）每一个接收节点r∈R至少属于一种k播组。

2.2 分离子树

通过设计不同的对播发包策略将树状网络拓扑分解成不同的两层三链子树。此处所说的两层三链子树指的是对播实验中探测包经过的链路所组成的两层的二叉树，其中“链”并不是专指链路，它可能是链路也有可能是由多条链路组成的路径。如图4所示，以一个较为简单的四层非对称树状拓扑为例，链路针对如图4（a）所示树状网络拓扑，若发包策略为C={＜2，5＞，＜3，6＞}，其中的对播组＜2，5＞将树状网络拓扑分离为如图4（b）所示的两层三链子树T2，5，“三链”分别由链路1、链路2和路径 P1，5组成。同理，若C={＜2，3＞，＜5，6＞}，对播组＜5，6＞则可得到如图4（c）所示的两层三链子树T5，6。

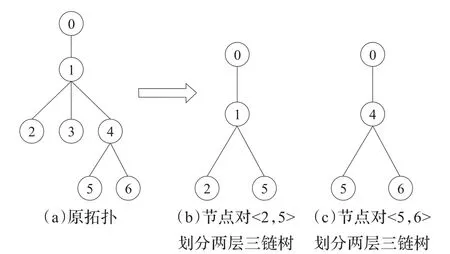
图4 通过不同的发包策略分解成不同的两层三链子树

用T表示k播组的子树，其中V表示节点，E表示链路。用 Xk={0，1，…，b}表示所有可能的链路时延。每个x∈X是一个|E|元。定义函数 y(x，T)为在C策略中从x∈X中提升给端到端时延提升。把端到端时延的所有可能性定义为Y={y(x，T)|x∈X}。用γ(y)=P{Y=y}来定义端到端实验结果的概率。

如图4（b）所示，假设发送探测包到节点对＜2，5＞，b=1，那么 Xk∈{0，1}，链路E={1，2，4，5}，实际链路时延分别为0，1，0，1。则可以得x={0，1，0，1}，测得路径时延为y=(1，1)，那么链路时延概率如下所示：

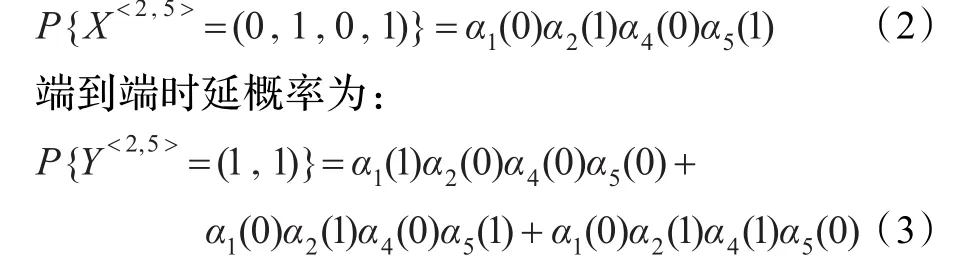
上述中测得路径时延是所有可能链路时延情况概率之和，可以将上述等式泛化为普遍情况。因此，离散无参数分布框架可表示为路径级数据多项式[11]。得到的观测值包括多次观测到的 y值，观测次数用N来表示，则得到的似然等式如下所示：

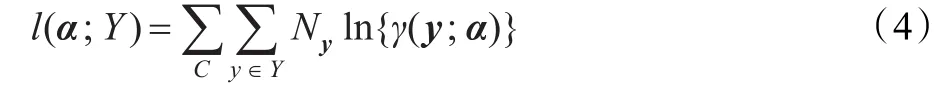
这个问题是典型的不完整数据估计问题，此等式很难直接得到最大似然的估计结果。贝叶斯算法[11]已应用到丢包率的分布估计之中，但是由于其依赖于先验概率分布和不符合上述文中不选择某一种特定的网络参数模型概括所有链路时延分布的假设情况，EM算法[12]可以解决此问题，如果这些观测数据是已知的，那么通过足够多次的端到端的探测实验，便可以很容易得到最大似然。

假设这些观测数据是已知的，则可以通过足够多次的端到端的探测实验得到最大似然。得到最大似然的步骤（分为E步骤和M步骤）如下所示：

E步骤：假设已经得到上一次迭代结果向量α(q-1)，首先，可以计算每条链路测量次数的期望值，得到的期望值如下所示：

然后利用这一期望值去计算链路k上探测包时延是i的次数N，得到的结果如下所示：

其中，公式（5）和公式（6）中的参数N表示实验中观测次数，公式（6）中的Mk，i是发包策略C中k链路上时延为i的总的数学期望。

M步骤：

其中，公式（7）中的参数mk是k链路上探测包测量的总次数。对于EM算法的迭代复杂度的研究，首先需要考虑对播组发包策略。每一个对播组实验有|T|个链路时延可能结果，所以有b|T|个链路时延结果。而对所得的每个结果需要加入端到端链路时延的可能性计算之中，因此，每一棵子树的E步骤的时间复杂度为O{b|T|}，而M步骤则由|Eb|个部分所组成。

2.3 移植算法

2.2节介绍的算法可较好地适应树状网络拓扑广度规模的扩展，可估计得出发包策略C中所有两层三链子树三条“链”的时延分布，但是无法做到网络拓扑的深度链路时延估计，因为并不是每一条“链”都是链路，其中存在部分路径，路径由多条链路所组成，本节将使用移植算法剥离路径中的链路时延。

移植算法GE（Grafting Estimation）的基本原理是用已知路径和链路的时延分布推算未知链路的时延情况。如图5所示，路径P1，5为图4（b）中两层三链子树T2，5中的一条“链”。其中，路径P1，5的时延已由上一节估算可知，而链路5的时延也可通过其他发包策略得出，例如图4（c）所示发包策略。因此，使用移植算法通过已知的路径P1，5和链路5的时延计算未知链路4的时延情况。

图5 移植算法

移植算法是一种固定点剥离方法，已知链路可能时延值的概率，将其固定，根据似然等式通过EM算法的多次迭代计算未知链路的值。在一条路径上发送n个探测包，nd是路径上时延值为d的次数。于是

E步骤：

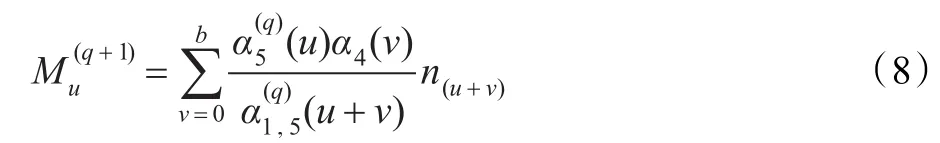
其中，Mu是未知链路k上时延值为u的期望，α(u+v)是路径时延为u+v的概率，α4(v)是链路4时延为v的概率，在公式（8）中α1，5是根据α4的更新而变化的。

M步骤：

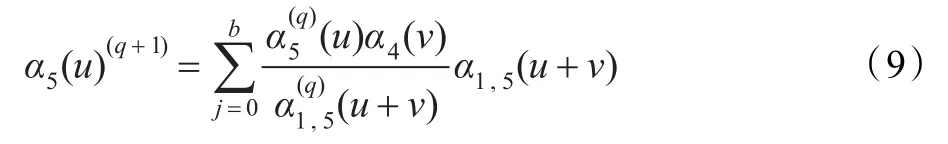
普通的EM算法的计算量随链路数量的不断增长迭代次数呈指数增加。而移植算法的计算量随各条链路中bin的增长链接所需的平均迭代次数呈线性增加。因此，通过不同发包策略的组合，此算法可以较好把握EM算法的尺度，复杂性为一个关于bin数量的三次多项式，从而可在一定程度上改进最大似然计算的复杂程度，通过链路的移植使得计算速度也可响应得以提高。

移植算法并不只适用于如图5所示两端链路的路径，它可推广于多段链路组成的路径之中，依次剥离每一条链路。假设路径 Pi，j由节点i，i+1，i+2，…，k，…，j组成，则剥离过程描述如下：

（1）已知路径Pi，k时延，通过其他发包策略估计所得。

（2）将路径Pi，j分解为路径Pi，k和路径Pk+1，j。

（3）通过已知的路径 Pi，j和路径 Pi，k的时延分布，使用移植算法估计路径Pk+1，j时延情况，因此EM算法的公式（8）和公式（9）可演变为：

E步骤：

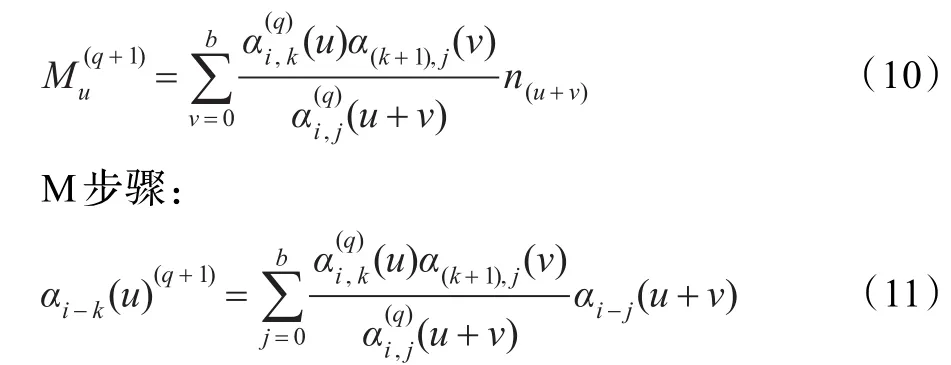
（4）分别针对路径Pi，k和路径Pk+1，j重复（1）步骤，直到计算出路径Pi，j中所有链路i，i+1，i+2，…，j的时延分布情况。

其中，若路径Pi，j中 j=i+1，则路径Pi，j表示链路j。

因此，设计不同的发包策略，在不同组播实验中，对仅单一接收节点的单播实验也可通过移植算法剥离确定每条链路的时延情况。

离散数据方程对一些链路可能导致估计值并不唯一。因为使用不同的发包策略或者不同发包策略组合可能计算出不同的时延估计值。针对这一问题，最简单的解决方法是将这些计算结果用加权平均数的方法结合起来。

其中，n表示探测包个数，α⌒表示链路时延估计值。最终移植算法计算产生的估计是一致的或渐近的。

图6 估计结果与真实值比较

该算法的复杂度较MLE算法直接估算有了明显的简化。根据公式（1）可知，根据测量数据Y和非满序矩阵对向量X进行逆估计较为困难，尤其是针对大规模网络问题计算量更是呈指数上升。虽然MPLE算法一定程度上减少计算量，但链路矩阵的分块问题并不容易解决。该算法将拓扑两步划分，首先划分为两层三链子树，然后进行路径的分段，这就将最大似然的估计问题大大化简，对两步划分子树分别使用EM算法进行计算，使得计算量始终维持在EM算法可计算的尺度之内。

3 仿真实验

针对以上文中提出的算法，下面将利用一个例子来说明，使用NS2模拟真实的网络环境对其内部链路时延分布进行估计，以验证之前提出算法的可行性。

对图4（a）所示网络拓扑进行实验。根节点0到节点1核心路由器之间的链路带宽为500 Mb/s，叶子节点的带宽为50 Mb/s，而其余路由器之间的连接使用300 Mb/s的带宽，详细实验参数如表1所示。R核心路由器背景流量主要由TCP和UDP连接组成。TCP需要确认是否连接成功或者接收数据包是否接收成功，因此TCP连接会响应网络拥塞状况；而UDP连接并没有上述确认过程，因而UDP没有逻辑连接状态，从而基本不会影响网络内部状态。在网络内部，背景流量由6个TCP连接和1个UDP连接构成。探测包使用40位的组播UDP数据包。

表1 链路参数配置表

每1/10 s，随机从方案C={＜2，3＞，＜5，6＞，＜3，5＞，＜2，6＞}中选择一组做探测包发送实验，如选中＜2，3＞，则从源节点0向叶子节点2和3发送组播探测包，节点2和3接收探测包并记录下时延情况。每一组的探测过程持续30 s，先后做10组测试实验，总共发送约3 000个探测包。同样的实验方法对其余3个测量节点对＜5，6＞，＜3，5＞，＜2，6＞进行探测包发送实验。用bin将测量所得数据离散化，其中假设q=0.25，p=0.2。图6展示了估计的结果以及与真实情况的对比。

由图6可以看出，在离散数据模式下，对于链路1、链路4、链路5三条链路，MPLE算法和移植算法两种方法所得估计值均围绕真实结果上下浮动，基本符合真实网络状况。两者相比，MPLE算法更加精准一些，但是精准度没有明细的差距。进一步分析图形分布可以看出，移植算法估计值与真实结果相比，普遍偏差最大的位置发生在时延为0值（即αk(0)）时，其估计值略小于真实值，而且随着探测包在路径中的传送过程之中，偏差会进行向下传递，使得偏差逐步增大。但是随着时延值的增长偏差则越来越小，估计值趋于与真实结果重合。在不断的实验中摸索修正偏差的方法，调整bin值的大小，并根据不同的bin进行相应的矫正计算。

4 结束语

网络链路时延分布估计始终基于时间和空间的独立性这一假设。在此广义的框架下，利用固定大小的bin将链路时延离散化。并不采取MPLE算法中将拓扑矩阵划分的方法，转而运用灵活发包策略将树状网络拓扑进行子树划分，该方法将大规模的逆概率估计问题分解成众多子问题，简化最大似然估计量。然后，针对不同的子树划分进行深度估计的研究，剥离路径时延以获取路径中每条链路的时延分布。与MPLE算法相比，减小了计算复杂度，计算速度也相应缩减，其预测结果从图6中可以看出依然保持较高的精准度，一定程度上解决了原有EM算法无法适应大规模网络的问题。不仅能够对网络断层扫描的拓扑推断技术[13]做出更好的指导作用，而且还可用于实际服务质量的监测以及问题链路的定位[14]。其不足在于估计过程中bin大小的选择，在内部链路统计未知的情况下，准确选择bin的尺寸是比较困难的，需在反复的实验中不断调整bin值的大小，以达到误差值与计算量的平衡点。

[1]钱峰.网络层析成像研究综述[J].计算机科学，2006，33（9）：12-17.

[2]Sun Yi，Li Dong，Sun Hongjie.Network tomography and improved methods for delay distribution inference[C]// ICACT，2007：1433-1437.

[3]赵洪华，陈呜.基于网络层析成像技术的拓扑推断[J].软件学报，2010，21（1）：133-146.

[4]Xia Ye，Tse D.Inference of link delay in communication network[J].IEEE Journal on Selected Areas in Communications，2006，24（12）：2235-2248.

[5]Presti F L，Duffield N G，Horowitz J，et al.Multicast-based inference of network-internal delay distributions[R].Univ Massachusetts，Amherst，MA，1999.

[6]Liang G，Yu B.Maximum pseudo likelihood estimation in network tomography[J].IEEE Trans on Signal Process，2003，51：2043-2053.

[7]李贵山，蔡皖东.网络链路时延分布估计方法研究[J].计算机工程与应用，2009，45（8）：20-22.

[8]Brian E，Gautam D，Paul B，et al.Toward the practical use of network tomography for Internet topology discovery[C]// 2010 Proceedings IEEE INFOCOM，2010：1-9.

[9]张宏莉，方宾兴，胡铭曾.Internet测量与分析综述[J].软件学报，2003，14（1）：110-116.

[10]孙红杰.基于主动测量的网络性能分析[D].哈尔滨：哈尔滨工业大学，2008.

[11]杜艳明，韩冰，肖建华.基于贝叶斯模型的IP网拥塞链路诊断算法[J].计算机应用，2012，32（2）：347-351.

[12]Yolanda T，Mark C，Robert D N.Network delay tomography[J].IEEE Transactions on Signal Processing，2003，51（8）：2125-2136.

[13]Jin Xing，Tu Wangqing，Gary C S H.Scalable and efficient end-to-end network topology inference[J].IEEE Transactions on Parallel and Distributed System，2008，19（6）：837-850.

[14]赵佐，蔡皖东.基于简单网络断层扫描的失效链路定位研究[J].计算机科学，2010，37（1）：108-110.

[15]Coates M，Nowak R.Network tomography for internal delay estimation[C]//IEEE Int Conf Acoust，Speech，and Signal Proc，2002.

WU Chenwen,LI Peiru,RU Junnian,LIU Xiangli

Institute of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

The link performance inference is crucial to network quality assessment,however usually the present assessment methods can only infer the simple network with definite layer and can’t be applied to the large scale network.This paper proposes a maximum likelihood estimation based on incomplete data to estimate the delay distribution of the inside network. This method divides the tree-like network topology into different two-layer binary subtrees and estimates every chain’s delay of every subtree.And then the link delays are divided into every link through the transplantation algorithm and every subtree is done in this way with this method one by one,thus the link delays of the whole network are obtained.The feasibility and accuracy of the algorithm are verified through NS2 simulation.

network tomography;delay distribution;Expectation Maximization（EM）algorithm;grafting estimation;delay estimation

对于网络质量评估链路性能推测无疑是至关重要的，然而现有的估计方法通常只能推测层次数有限的简单网络，无法应用于大规模网络。提出了一种基于不完整数据极大似然估计算法，估计网络内部链路时延分布，该方法通过不同的发包策略将树状网络拓扑划分成不同的两层三链子树，针对每个子树估计每条“链”的时延，随后通过移植算法将路径时延划分到各链路中，逐一对每个子树使用该方法计算从而得到整个网络链路时延情况。利用NS2仿真实验验证了该算法的可行性和准确性。

网络断层扫描；时延分布；最大期望（EM）算法；移植算法；时延估计

A

TP393

10.3778/j.issn.1002-8331.1301-0171

WU Chenwen,LI Peiru,RU Junnian,et al.Discrete delay distribution inference based on end-to-end measurement. Computer Engineering and Applications,2014,50（24）：76-80.

甘肃省自然科学基金（No.1308RJZA111）；兰州市科技计划基金资助项目（No.2009-1-5）。

吴辰文（1964—），男，教授，主研方向为网络断层扫描技术；李培儒（1984—），男，硕士研究生；茹俊年（1986—），男，硕士研究生；刘香丽（1986—），女，硕士研究生。

2013-01-16

2013-05-06

1002-8331（2014）24-0076-05

CNKI网络优先出版：2013-08-07，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130807.1540.003.html