加权平均集成神经网络模型在城市需水预测中的应用
崔东文
(云南省文山州水务局,云南文山 663000)
1 研究背景
城市需水量预测是给水系统规划与管理的重要内容之一,也是制定水资源发展战略的重要环节[1],准确有效地预测需水量对社会经济和环境的协调发展具有重要的意义。传统需水预测一般采用定额法、时间序列法、回归分析法以及灰色预测法等方法,这些传统方法忽视了需水诸影响因素间动态相互制约的关系,存在预测精度不高等问题和不足[2-3]。城市需水预测是以经济发展特征和用水现状为基础,受到城市规模、社会经济发展水平和政府政策等诸多相关因素的影响,是一个典型的多层次复杂非线性系统,适宜借助人工神经网络(artifical neural network,ANN)等智能算法来解决其高维、非线性预测问题。ANN中的BP神经网络(backpropagation network,BP)和 Elman神经网络在城市需水预测中得到了广泛应用[4-5]。然而在实际应用中,BP神经网络存在着学习收敛速度慢、易陷入局部极值等不足。为克服BP算法中的不足,基于附加动量法、自适应速率调整法、弹性算法、拟牛顿法、共轭梯度法、Levenberg-Marquardt法以及遗传算法(genetic algorithm,GA)等智能算法优化BP网络权值阈值等的改进算法被提出[6-8],并在改进的BP神经网络算法中得到了应用[5,9]。Elman神经网络是一种典型的动态神经元网络,其网络结构及算法较BP神经网络有较大改善,但由于Elman神经网络是在BP神经网络的基础上改进而来,也采用BP神经网络算法进行权值修正,因此同样存在着学习速度较慢,易陷入局部极值等缺点。支持向量机(support vector machine,SVM)是一种通用的前馈神经网络,用于解决模式分类和非线性映射问题。SVM具有严谨的数学基础,通过统计学习中的VC维(vapnikchervonenkis dimension)理论和寻求结构风险最小化原理来提高泛化能力,已成为继ANN之后机器学习领域新的研究热点,其最小结构风险二次规划寻优理论、支持向量决定SVM拓扑结构、支持向量数目决定计算复杂程度的三大优势决定了它在机器学习领域有着举足轻重的地位[8,10-11]。集成预测是Bates等[12]在1969年提出的组合预测思想,其目的是为了有效地利用各种模型的优点,将不同的预测方法进行适当组合,综合利用各种方法所提供的信息,从而尽可能提高预测精度。实践表明,不同的预测方法往往有不同的预测结果,不同的预测方法能挖掘不同的有用信息,不同模型的预测结果通常具有互补性,其预测精度也各有悬殊。没有一种适用于所有预测的通用方法,任何一种预测方法都有其适用性和局限性,因此应依据实际问题选择适当的模型与方法[13]。
在实际应用中,决定预测模型精度的关键因素是问题本身的复杂程度,针对不同问题选择恰当的预测方法是决定预测效果优劣的关键。基于此,笔者针对上海市需水预测的小样本容量问题,经过调试和筛选,选用SVM、BP和Elman神经网络作为基本预测模型,并利用下述方法提高 SVM、BP和Elman单一模型的预测精度和泛化能力:一是采用交叉验证法(cross validation,CV)确定SVM模型中的惩罚因子c和核函数参数g;二是针对BP、Elman神经网络标准算法收敛速度慢、易陷入局部极值的不足,采用自适应动量算法改进BP、Elman神经网络标准算法;最后,基于集成预测的思想,采用加权平均方法构建综合集成预测模型,并以上海市2002—2011年需水量预测为例,以验证加权平均集成模型的预测精度。
2 预测模型简介
2.1 支持向量机(SVM)
SVM是20世纪90年代中后期发展起来的基于统计学习理论而构建的典型神经网络。SVM用于回归时,其基本思想不再是寻找最优分类面将样本分开,而是寻找一个最优超平面,使得所有训练样本离该最优超平面距离最短,这个超平面可看作拟合好的曲线。SVM类似于一个3层前馈神经网络,其隐层节点数对应于输入样本与一个支持向量机的内积核函数,输出节点数对应于隐层输出的线性组合。SVM神经网络拓扑结构及算法步骤可参阅笔者论文[8,14]及相关文献[10-11]。
2.2 BP与Elman神经网络
BP神经网络是一种单向传播的多层前馈神经网络,主要特点是信号前向传播,误差反向传播,其算法的精髓是将网络的输出与期望输出间的误差通过反向传播分摊到各神经元的权值和阈值,通过多次迭代使BP神经网络的预测输出不断逼近期望输出。由非线性变换单元组成的BP神经网络,不仅结构简单(仅含输入、输出和隐节点3层),而且具有良好的非线性映射能力,主要应用于函数逼近、模式识别、分类和数据压缩等领域。限于篇幅,其网络拓扑结构及算法步骤可参阅笔者的研究[9,15-17]及相关文献[6-7,11,18]。
Elman神经网络是Elman于1990年提出的,该模型是在前馈式网络的隐含层中增加了一个承接层,作为一步延时算子,以达到记忆的目的,从而使系统具有适应时变特性的能力,能够更生动、更直接地反映系统的动态特性。与BP神经网络本质上的区别是,Elman网络既有前馈连接,又有反馈连接,能有效克服BP神经网络不具备动态特性的缺点。Elman神经网络同样可以以任意精度逼近任意非线性映射,工程中主要用于动态预测,在函数逼近、模式识别等方面也均有应用,其网络拓扑结构及算法步骤可参阅笔者论文[9,16,19]及相关文献[6-7,11,18]。
2.3 BP与Elman神经网络算法的改进
由于BP和Elman神经网络均是采用梯度下降算法,其权值和阈值的调整是沿着误差函数下降最快的方向——负梯度方向进行的。梯度下降算法在最初几步下降较快,但随着接近最优值,梯度趋于零,误差函数开始下降缓慢,陷入局部极值。针对BP和Elman神经网络算法中的不足,笔者采用自适应动量算法改进标准梯度下降算法。自适应动量算法是将附加动量法和自适应学习速率调整法结合起来,利用二者的优点,大大提高BP和Elman神经网络的收敛速度和预测精度。自适应动量算法的原理及步骤[6-7,9,18]简述如下:
步骤一:附加动量法。附加动量法是在反向算法的基础上,在每一个权值变化基础上增加一项正比于前次权值变化量的值,并根据反向算法来产生新的权值变化。附加动量法权值、阈值的调节公式为
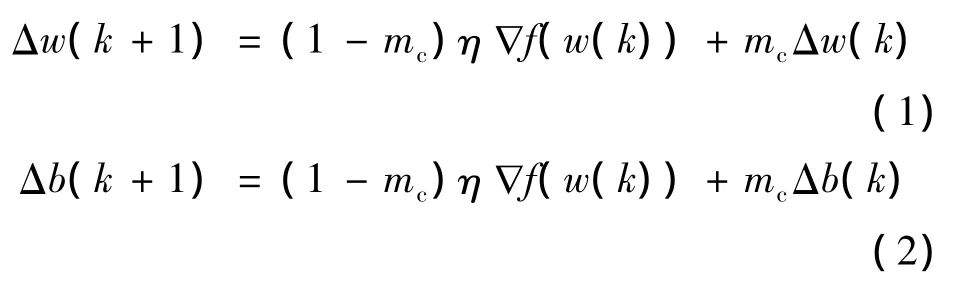
式中:k为训练次数;η为学习速率;mc为动量因子,一般取0.95左右;∇f(w(k))为误差函数的梯度;Δw为权值变化量;Δb为阈值变化量。
附加动量法实质是将最后一次权阈值的变化通过一个动量因子来传递,当增加动量项后,使得权阈值调节向着误差曲面底部的平均方向变化,当网络权值、阈值进入误差曲面底部的平坦区时,∇f(w(k))变得很小,此时 Δw(k+1)≈Δw(k),从而避免了Δw=0情况的出现,有助于使网络从误差曲面的局部极小值中跳出。合理使用权值修正公式的判断条件为
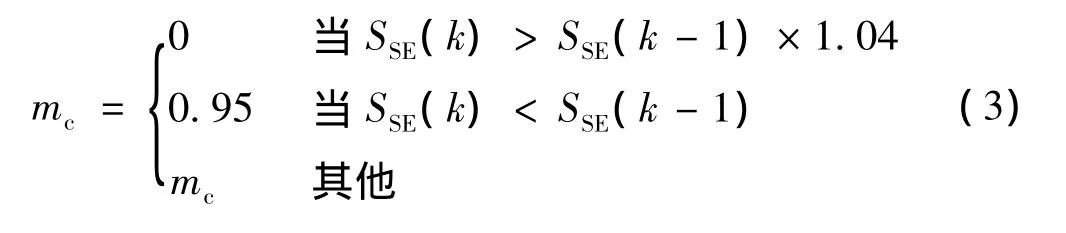
式中:SSE为网络误差。
步骤二:自适应学习速率调整法。上述式(1)和式(2)中学习速率η的选择对于网络训练及预测效果的影响较大,η选择太大,将导致误差值SSE来回振荡;η选择太小,则导致太小的动量能量,从而使网络只能跳出很小的“坑”,而对于较大的“坑”或“谷”则无能为力,这必然对学习速率η的选择带来困难。为了解决学习速率η的选择问题,提出了自适应学习速率调整法。自适应学习速率调整公式为

式中,学习速率η可根据误差值SSE的大小自动调整。当新SSE超过旧SSE一定的倍数时,学习速率将减小;否则其学习速率保持不变;当新SSE小于旧SSE时,学习速率将增加。该方法可以保证网络总是以最大可接受的学习速率进行训练。
自适应动量算法综合了附加动量法和自适应学习速率调整法的优点,具有收敛速度快、预测精度高、不易陷入局部极值等优点,在BP和Elman神经网络算法中得到了广泛应用。
2.4 集成预测方法
加权平均预测法是依据各单一模型预测效果的优劣给出不同的权重,然后求加权平均值,以加权平均值作为集成模型预测值[20-21]。加权平均值¯x的计算公式为
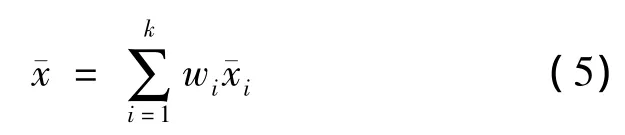
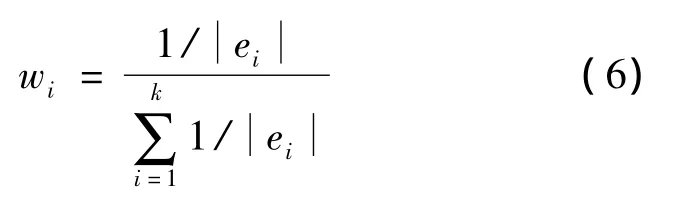
2.5 集成预测步骤
基于上述SVM、BP和Elman神经网络基本原理和集成预测方法,加权平均集成神经网络模型实现需水预测的步骤可归纳如下:
a.确定输入向量。利用相关分析和多重线性回归P值检验的方法遴选出与需(用)水密切相关的影响因子,利用ADF进行单位根检验,对所选取的影响因子原始序列进行平稳性检验,对不平稳的序列进行差分,确定影响因子原始序列的平稳性和模型的输入向量。
b.引入虚拟维。由于需水预测序列时间较短,经调试,各单一模型预测的精度达不到基本精度要求。为保证各单一模型的预测精度和泛化能力,避免模型过度拟合,引入噪声变量,即虚拟维。
c.构建模型。依次构建SVM、BP和Elman单一需水预测模型,利用训练样本对模型各相关参数及结构进行调试和率定,在各单一模型处于最佳预测效果时确定相关参数及结构,并计算各模型的预测值和预测误差绝对值。
d.确定权重。利用公式(6)计算各单一模型的权重。
e.利用集成模型进行需水预测。利用集成预测模型公式(5)对需水量进行预测和分析。若集成模型预测值达不到期望精度和泛化能力的要求,则反向对各单一模型进行调试和预测,直至集成模型预测值满足期望精度的要求。
3 应用实例
3.1 数据来源与数据分析
以上海市为例,收集上海市1980—2011年的年用水量及相关数据。进行相关分析可知,上海市1980—2011年用水序列与户籍人口、轻工业产值、重工业产值、建筑业总产值、农业总产值和服务业产值的相关系数均大于0.8,需水序列与社会、经济相关序列之间存在着较强的相关性。鉴于输入变量间高度相关易导致多重共线性问题的发生,进而影响模型的泛化能力和预测精度,因此,本文利用多重线性回归P值检验的方法从户籍人口等6个指标中遴选出户籍人口、轻工业产值和服务业产值3个因子作为输入变量,并利用E-views软件对需水量、户籍人口、轻工业产值和服务业产值序列进行ADF单位根检验,得知需水量、服务业产值序列为一阶平稳,户籍人口和轻工业产值序列为二阶平稳,表明需水量、户籍人口、轻工业产值和服务业产值为平稳序列,可用于预测。上海市1980—2011年各需水预测指标序列见表1。
从表1可以看出,1982年、1988年、1999年和2009年用水量较前一年有所下降,这与一定时期内用水量变化趋势不相吻合。为避免模型过度拟合,有效提高模型的预测精度和泛化能力,笔者引入噪声变量,即虚拟维。引入原则是:1982年、1988年、1999年和2009年的噪声变量设置为0,其余各年噪声变量按用水量年度增幅大小设置为0.05~0.3不等(各序列归一化范围为0~0.5),若年度用水量增幅小于0.5亿m3,则噪声变量设置为0.05;小于1亿m3,设置为0.1;小于1.5亿m3,设置为0.2;大于1.5亿m3,设置为0.3;对于“未知”样本,可按年度用水量增幅小于0.5亿m3计,即噪声变量设置为0.05。
3.2 需水预测的实现
3.2.1 数据归一化处理
由于需水预测影响因子具有不同的物理意义和不同的量纲及数量级,因此,在网络训练前需对原始数据进行归一化处理,公式为
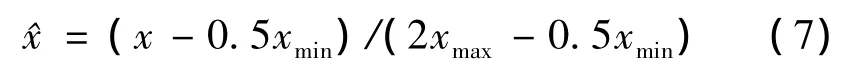
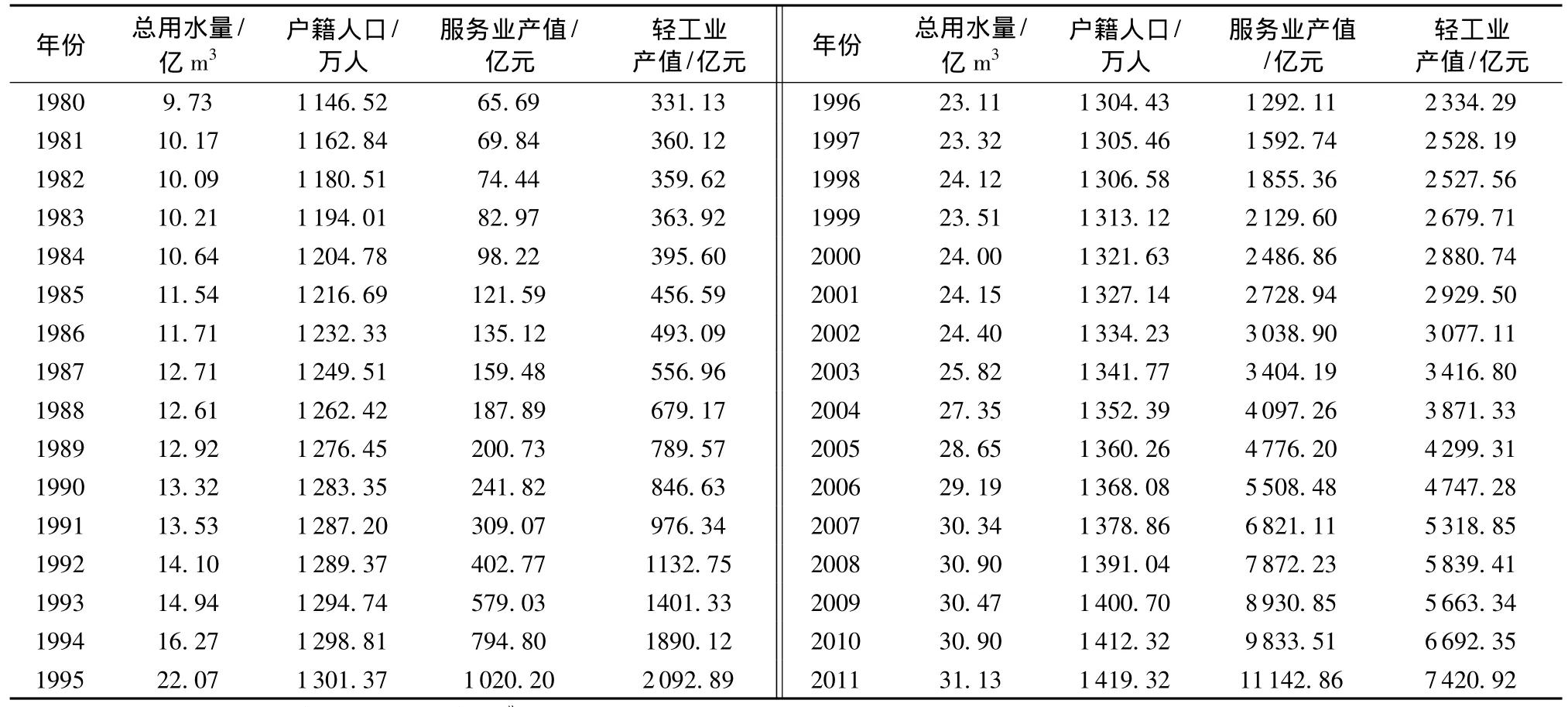
表1 上海市1980—2011年用水量及其影响因子情况
3.2.2 网络训练
本研究以1980—2011年影响上海市需水量的相关因子建模,以户籍人口、轻工业产值、服务业产值以及虚拟维作为网络输入,需水量作为输出,构建4输入1输出的神经网络模型;以1980—2001年的22组数据作为网络训练样本;2002—2011年10组数据作为网络预测检验样本。基于MATLAB环境,创建及训练SVM、BP和Elman神经网络模型,进行需水量预测。经反复调试,在下述参数设置条件下,SVM、BP和Elman神经网络模型具有较好的预测效果。
SVM模型:基于libsvm工具箱,选择径向基核函数为SVM的核函数。设置惩罚因子c和核函数参数g的搜索空间,均设置为2-2~26,k取值 2,g和c的步进大小均取0.5,参考文献[8]和[14],利用交叉验证法(cross validation,CV)确定模型中的惩罚因子c和核函数参数g分别为2.44528和0.25时(其他参数采用默认值),SVM模型性能达到最优。
BP模型:对BP神经网络各隐层神经元数的选取,目前并没有统一的计算方法,主要做法是:先依据Kolmogorv定理得出一个初始神经元数,然后利用逐步增长或逐步修剪法确定最终神经元数。本文参考文献[13]、[17]和[21],最终确定 BP神经网络模型的模型结构为4-4-1,隐含层和输出层传递函数均采用logsig,训练函数采用traingdx,设定期望误差为0.0001,最大训练轮回为5000次(其他参数采用默认值),此时该模型性能达到最优。
Elman模型:做法同BP神经网络模型,最终确定Elman神经网络模型的模型结构为4-3-1,隐含层和输出层传递函数均采用logsig,训练函数采用traingdx,设定期望误差为0.000 1,最大训练轮回为2000次(其他参数采用默认值),这时,Elman模型性能达到最优。
3.3 集成预测模型权重的确定
按照上述集成预测方法和步骤,利用SVM、BP和Elman神经网络模型需水量预测值的平均相对误差绝对值来确定其各自权重。通过计算,SVM、BP和Elman 3种模型的集成预测权重依次为0.386 8、0.4025和0.2106。
3.4 需水预测结果及分析
利用上述训练好的SVM、BP和Elman神经网络模型以及加权平均集成模型对上海市2002—2011年需水量进行预测,预测结果见表2。
分析表2和表3,可以看出:①利用加权平均集成模型对上海市2002—2011年进行需水预测的平均相对误差为1.8004%,最大相对误差为3.6995%,精度和泛化能力均大幅优于各单一模型,表明该模型用于需水预测是合理可行而有效的。加权平均集成模型综合了各单一模型的优点,有效避免了单一模型预测误差过大和不稳定的缺点,具有预测精度高、泛化能力强、误差变化平稳的等特点。②就各单一模型进行比较,SVM模型的精度和泛化能力要优于BP模型和Elman模型,且SVM模型具有较大的权重,这在很大程度上克服了简单平均集成方法的不足,保证了集成模型的预测精度和泛化能力。③整体而言,各单一模型预测的平均相对误差绝对值均小于5%,最大相对误差绝对值均在8%以内,在一定程度上均能满足需水预测精度的要求。但从实际预测结果来看,BP模型预测结果偏大,Elman模型预测结果偏小,SVM模型预测结果略偏大,但各单一模型都具有较好的互补性,从而保证了加权平均集成模型具有较高的预测精度和泛化能力。
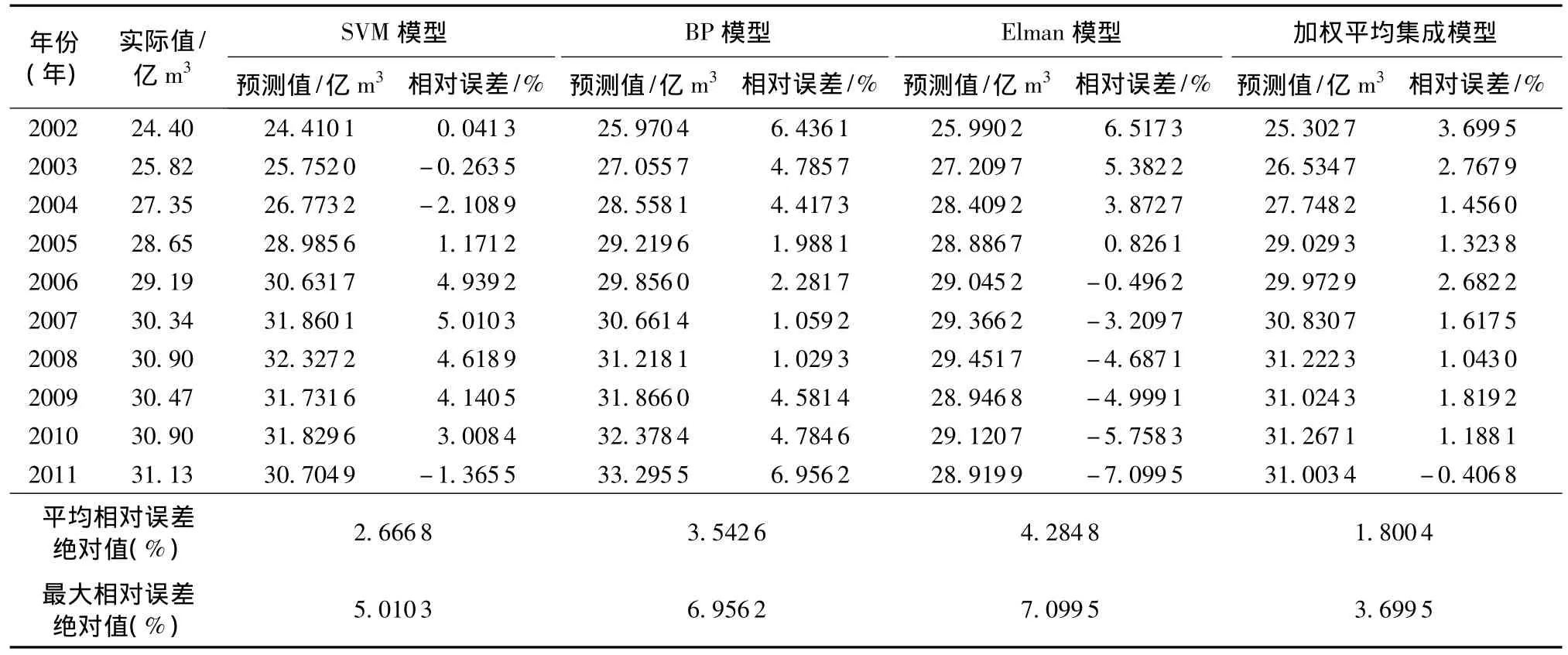
表2 几种模型对上海市2002—2011年需水量预测的结果及其比较
4 结语
本研究建立了基于SVM、BP和Elman神经网络的加权平均集成需水预测模型,该模型很好地综合了各种单一模型的优点,克服了单一模型预测误差过大和不稳定的缺点,在预测精度、泛化能力和误差稳定性方面较单一模型均有较大提高,使得验证实例的预测结果达到理想状态。在利用加权平均集成模型进行需水预测中,有两个关键之处值得借鉴:①集成模型预测精度取决于各单一模型的预测精度和模型间的互补性。互补性是指各单一模型预测平均相对误差与各自权重之积的和趋近于0,越趋近于0,表明模型间的互补性越强,互补性越强也就意味着集成模型的预测精度越高。②引入噪声向量,即虚拟维,避免模型过度拟合,可有效提高模型的预测精度和泛化能力。
[1]陈坤.上海水资源可持续利用的经济学研究[M].上海:上海人民出版社,2007.
[2]张灵,陈晓宏,谢毅文.投影寻踪在珠海市需水预测中的应用[J].人民长江,2008,39(6):41-43.(ZHANG Ling,CHEN Xiaohong,XIE Yiwen. Application of projection pursuit in Zhuhai water demand forecasting[J].Yangtze River,2008,39(6):41-43.(in Chinese))
[3]刘卫林.几种需水量预测模型的比较研究[J].人民长江,2008,39(6):19-22.(LIU Weiling.Several water demand prediction models comparative study[J].Yangtze River,2008,39(6):19-22.(in Chinese))
[4]崔东文,郭荣.BP神经网络模型与灰色GM(1,1)模型在需水预测中的应用[J].水资源保护,2012,28(3):19-22.(CUI Dongwen,GUO Rong.BP neural network model and gray GM(1,1)model in water demand prediction[J].Water Resources Protection,2012,28(3):19-22.(in Chinese))
[5]崔东文.基于改进的Elman神经网络在需水预测中的应用[J].水电能源科学,2013,31(8):38-41.(CUI Dongwen.Aplication of GA-Elman multivariate water demand forecasting model[J].Water Resources and Power,2013,31(8):38-41.(in Chinese))
[6]张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009.
[7]张良均,曹晶,蒋世忠.神经网络实用教程[M].北京:机械工业出版社,2008.
[8]崔东文.支持向量机在水资源类综合评价中的应用研究:以全国31个省级行政区水资源合理性配置为例[J].水资源保护,2013,29(5):20-27.(CUI Dongwen.Support vector machine for comprehensive evaluation of water resources:application to reasonable allocation of waterresourcesin 31 provincial-leveladministrative regions in China[J].Water Resources Protection,2013,29(5):20-27.(in Chinese))
[9]崔东文.基于改进BP神经网络模型的区域水资源脆弱性综合评价[J].长江科学院院报,2013,30(2):1-7.(CUI Dongwen.Comprehensive assessment of the water resources by improved BP neural network model[J].Journal of Yangtze River Scientific Research Institute,2012,30(2):1-7.(in Chinese))
[10]VAPNIK V N.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000.
[11]田景文,高美娟.人工神经网络算法研究及应用[M].北京:北京理工大学出版社,2006.
[12] BATES J M,GRANGER C W J.The combination of forecasts[J].Operational Research Quarterly,1969,20(1):451-468.
[13]郭彦,金菊良,梁忠民.基于集对分析的区域需水量组合预测模型[J].水利水电科技进展,2009,29(5):42-45.(GUO Yan,JIN Juliang,LIANG Zhongmin.Combined prediction model for regional water demand based on set pair analysis[J].Advances in Science and Technology of Water Resources,2009,29(5):42-45.(in Chinese))
[14]崔东文.支持向量机在湖库营养状态识别中的应用研究[J].水资源保护,2013,29(4):26-30.(CUI Dongwen.Application of support vector machine to lake and reservoirtrophic statusrecognition[J].Water ResourcesProtection, 2013,29(4):26-30.(in Chinese))
[15]崔东文.基于BP神经网络的文山州水资源承载能力评价分析[J].长江科学院院报,2012,29(5):9-15.(CUIDongwen.Evaluation and analysisofwater resources carrying capacity in wenshan prefecture based on BP neural network[J].Journal of Yangtze River Scientific Research Institute,2012,29(5):9-15.(in Chinese))
[16]崔东文.几种神经网络模型在湖库富营养化程度评价中的应用[J].水资源保护,2012,28(6):12-18.(CUI Dongwen.Applications of several neural network models to eutrophication evaluation of lakes and reservoirs[J].Water Resources Protection,2012,28(6):12-18.(in Chinese))
[17]崔东文.多隐层BP神经网络模型在径流预测中的应用[J].水文,2013,33(1):68-73.(CUI Dongwen.Multilayers BP neural network model in runoff prediction [J].Journal of China Hydrology,2013,33(1):68-73.(in Chinese))
[18]丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社,2009.
[19]崔东文.改进Elman神经网络在径流预测中的应用[J].水利水运工程学报,2013,38(2):71-77.(CUI Dongwen.An improved Elman neural network and its application to runoff forecast[J]Hydro-Science and Engineering,2013,33(1):71-77.(in Chinese))
[20]郑莉,段冬梅,陆凤彬,等.我国猪肉消费需求量集成预测:基于ARIMA、VAR和VEC模型的实证[J].系统工程理论与实践,2013,33(4):918-925.(ZHENG Li,DUAN Dongmei,LU Fengbin,et al.Integration forecast of Chinese pork consumption demand:empirical based on ARIMA、VAR and VEC models[J]. Systems Engineering—Theory & Practice,2013,33(4):918-925.(in Chinese))
[21]崔东文.基于极限学习机的长江流域水资源开发利用综合评价[J].水利水电科技进展,2013,33(2):14-19.(CUIDongwen.Comprehensiveevaluation ofwater resources development and utilization in Yangtze River Basin based on extreme learning machine [J].Advances in Science and Technology of Water Resources,2013,33(2):14-19.(in Chinese))

