动态分维数在水库水质分析评估中的应用
陈吉江,毛洪翔,杨 森,夏国团,章卫军
(1.余姚市水利局,浙江余姚 315400;2.宜水环境科技(上海)有限公司,上海 200125)
富营养化防治逐渐成为水库饮用水水源地水质全面达标建设中的重要环节,对水库营养状态的中长期分析评价是富营养化防治的基础。笔者在对我国南方水库水质监测、预测、预警与应急决策支持系统技术研究课题中,除按照单因子评价方法对水库水质进行评价、采用营养状态指数对水库营养状态进行评价外,还就单因子动态分维数与综合指标动态分维数分析方法,对处于中营养~轻度富营养化状态的水库水质分析评估开展应用研究,对这两种方法的原理、步骤、应用成果(以SM水库为例)进行介绍,就有关问题进行讨论并提出建议。
1 单因子动态分维数分析
1.1 动态分维数原理
分形理论自1975年由美籍法国数学家曼德尔布罗特(B B Mardelbrot)正式提出以来,已发展成为数学的一个新分支,它研究自然界中没有特征长度但有自身相似的复杂现象,揭示复杂的自然和社会现象中所隐藏的规律性和层次性,在许多领域中得到广泛应用[1-4]。
非线性问题的解决一般从动力系统角度进行研究,现代非线性科学主要包括耗散结构理论、协同论、突变理论、混沌动力学、分形理论和人工神经网络[5]。分形维数是分形理论中核心的概念与内容,是表征分形特征的重要参数。分维数说明了研究对象在时空上分配的不规则性及其复杂程度,为量化和评价系统的随机变化程度提供了手段。欧氏空间的几何维数是整数,而分形的维数可以是分数。由于研究对象性质不同,常用的分维类型主要有相似维数、豪斯道夫(Hausdorff)维数、盒子维数、信息维数和关联维数等。目前所研究的整数维数和分数维数都是静态维数,即不考虑时间因素,如果在维数计算公式中引入了时间因素,所求出的维数随时间而变化,这样的维数称为动态维数,它描述了事物的发展变化规律[6]。
水质系统是一个复杂的系统,引起水质变化要素的时空变化具有非线性特点。运用分形理论进行分析,可从复杂水质系统运动中发现其内在的、有序的规律,更全面地揭示水质动力系统的复杂运动特征。以豪斯道夫分维数为基础,将时间因素引入其计算公式,求得一维动态豪斯道夫分维数Dft。

式中:x0,x1,x2,…,xt为时间序列;Xt-1,Xt,Xt+1为生成序列;K为“肯定性”;L为“否定性”;Dft为动态分维数。
Dft描述了事物发展的否定之否定规律,利用Dft可以判断出系统的临界点,从而将序列分期,揭示其动态变化规律。由此对处于中营养~轻度富营养化状态的水库水质变化过程进行分析评估。
1.2 单因子动态分维数分析方法
选择某一水质指标的实测序列,利用式(1)计算该指标的动态分维数。以时间为横坐标,动态分维数和水质实测指标为纵坐标,分别点绘动态分维数对时间的变化过程线和实测指标对时间的变化过程线(可以画在同一张图上)。然后,对这两条过程线进行分析、比较,寻找确定分维数截集。一个正确的截集应该保证分维数的变化与该指标的变化,特别是一些突变点,有规律的对应,使实测资料的变化过程和特征得到很好的解释。当分维数变化过程线上某一时刻的分维数值超过该截集时,预示该指标将发生大的变化(甚至突变);反之,该指标短期内一般不会发生突变。由此可知,这一分析方法对水库单因子分析评估工作具有很好的实用价值。
2 综合指标动态分维数分析
2.1 综合指标构建
水体富营养化是指大量的N、P等植物性营养元素排入流速缓慢、更新周期长的地表水体,使藻类等水生生物大量生长繁殖,有机物产生的速度远远超过消耗速度,水体中有机物积蓄,水生生态平衡被破坏的过程。水体富营养化的形成主要受营养物质,水文、气象、气候条件,水体动力学和更新周期等因素的影响[7-8]。
从评估水库富营养指标的角度出发,将TP、TN、CODMn、Chl-a、透明度加权为一个综合性指标,对该综合性指标的时间序列利用动态分维数分析方法,来揭示具有富营养化特征的水质系统变化规律和整体属性。综合指标加权平均公式如下:
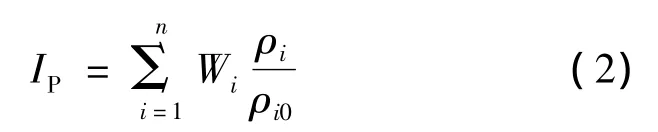
式中:IP为加权平均指数;ρi为第i项监测指标质量浓度,mg/L;ρi0为第i项评价指标标准质量浓度(选用水库Ⅱ类标准限值),mg/L;Wi第i项监测指标的权重系数。
权重系数Wi的确定通过各时间序列监测指标的数据向量进行相空间重构后,求得各自的关联维数 Ds[9],对Ds进行归一化处理后得到权重系数 Wi。
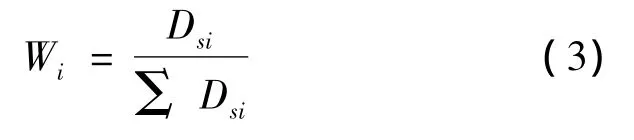
式中:Dsi为第i项监测指标的关联维数。
2.2 动态分维数分析方法
综合指标动态分维数分析方法与单因子动态分维数分析方法原则上相同,区别仅在纵坐标为综合指标,此处不再赘述。
综合指标分析法比单因子分析法更能反映水质系统的整体属性和变化趋势。当综合指标分维数过程线上某一时刻的分维数值超过截集时,表明水质可能发生大的变化(甚至突变);反之,水质即使有波动,一般也属于正常涨落,弛豫时间短。
3 应用实例
3.1 SM水库单因子动态分维数分析评估
3.1.1 水库概况
SM水库是我国南方的一座以供水为主,兼顾防洪、灌溉、发电、养鱼等综合利用的中型水库。自2005年开始每月定期监测,监测指标包括水位、水温、pH、DO、CODMn、NH3-N、TP、TN、Cu、Zn、As、Hg、Se、Fe、Mn、Cr6+、F-、CN-、Cl-、SO42-、NO-3-N、挥发酚、阴离子表面活性剂、BOD5等共24项,其中阴离子表面活性剂、BOD5从2010年1月开始监测。
3.1.2 富营养化评价
20世纪初,国内外学者对水体富营养化评价方法提出了一些切实可行的方法,如污染损害指数法[10]、模糊综合评价法[11]、综合水质标识指数法[12]、人工神经网络法[13]等。本文采用 SL 395—2007《地表水资源质量评价技术规程》中的湖(库)营养状态的指数法进行水库的富营养化评价。由营养状态指标IE判断:0≤IE≤20为贫营养;20<IE≤50为中营养;50<IE≤60为轻度富营养化。
SM水库在2005—2012年的8年间缺少透明度和Chl-a的长时间序列的监测信息,选择TN、TP和CODMn进行水库富营养化状态评价,将 TN、TP和CODMn的年均值和季均值转换成赋分值后计算得到营养状态指标IE(图1)。
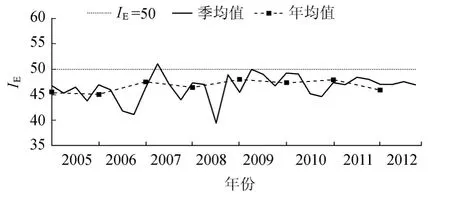
图1 SM水库2005—2012年TN、TP和CODMn的营养状态的年、季均值
由图1可知,SM水库营养状态从2005—2012年总体上处于中营养状态区间,离轻度富营养化评分数值的下限值(IE=50)较为接近。2005—2012年,除了2007年、2009年有逾过轻度富营养化下限值(IE=50)外,其余季度营养状态处于中营养状态区间,离轻度富营养化评分数值的下限值(IE=50)较为接近。由年均值富营养状态评价和季均值富营养状态评价结合分析可知,SM水库处于中营养~轻度富营养状态。
3.1.3 水质评价与指标选择
按照GB 3838—2002《地表水环境质量标准》,对SM水库水质进行单因子评价。在96个月的水质监测中,TN超标90次,TP超标13次、DO超标6次、Mn超标1次,pH不合格5次,总超标与不合格次数共计为115次。TN、TP、DO、Mn超标百分比分别为:78%、11%、5%、1%,pH不合格百分比为5%。选择超标最严重的因子TN进行单因子动态分维数分析。
3.1.4 动态分维数计算
对TN序列按式(1)进行动态分维数计算,2005—2012年ρ(TN)过程线、TN动态分维数过程线及截集见图2。
3.1.5 分析评估
SM水库TN动态分维数的截集取1.18时,当TN动态分维数点超过该截集水平时,TN浓度发生较大改变;当TN动态分维数点未超过该截集水平时,TN浓度波动幅度不大。
3.2 SM水库综合指标动态分维数分析评估
3.2.1 综合指标构建

图2 SM水库ρ(TN)过程线、TN动态分维数过程线及截集
根据对SM水库实测资料的分析,由于透明度、Chl-a的监测数据缺乏,因此,以TN、TP、CODMn3个因子的加权值作为综合指标值,权重系数取0.452、0.351和0.197。2005—2012年的综合指标过程线、综合指标动态分维数过程线及截集见图3。

图3 SM水库综合指标值过程线、综合指标动态分维数过程线及截集
3.2.2 动态分维数计算
3.2.3 分析评估
SM水库综合指标动态分维数截集取1.21,当综合指标动态分维数点超过该截集水平时,综合指标值急剧上升,水质系统发生了大的变化;当综合指标动态分维数点未超过截集1.21时,即使综合指标值有小的变化,水质系统也能在较短时间内返回平衡态。
综合单因子分析、富营养化评价、单因子动态分维数分析评估和综合指标动态分维数分析评估的有关成果的全面分析,说明SM水库具有富营养化特征的水质系统目前基本处于平衡态附近。此为防止SM水库水体富营养化的关键时机,建议抓住这一重要时机,进一步加大保护和治理力度,以取得事半功倍的效果。如果失去了这一时机,不但饮用水安全难以得到保障,严重影响经济发展,而且使治理的技术难度增大,治理周期延长,治理投资增加。
4 讨论与建议
a.对处于中营养~轻度富营养化状态的SM水库进行了综合指标分维数的应用探讨,未考虑不同营养状况的水库综合指标动态分维数的变化规律,建议今后扩大研究对象,开展不同营养状态水库分维数变化规律研究,归纳分析出不同营养状态的综合指标分维数截集。
b.对水库富营养化采取治理措施后的综合指标动态分维数变化未进行研究,建议开展相关跟踪研究。通过综合指标动态分维数对不同治理措施响应观察分析,进一步寻求动态分维数变化的物理意义,为优化治理方案提供支持。
c.加强对水质系统的理论研究,包括系统的结构、性态和动力学机制,如性态方面的形态拓扑量、标度性、渐进稳定性、结构稳定性、鲁棒性、灵敏性、随机性与趋极性等,进一步从系统整体上把握水质变化规律,提高对水库水质的预测水平和调控能力。
5 结语
作为探讨,作者对2005—2012年动态分维数在SM水库水质分析评估中的应用的可能性、方法步骤、实践结果进行了整理和总结。初步表明,按现行的水质分析规范要求,在全面做好水质分析的基础上,该方法作为一种辅助性的、补充性的、参考性的分析,对更全面地考察水库水质变化趋势具有一定价值。同时,如何正确使用这一方法还需要同行作深入的探讨与交流,如综合指标构建时对相关因子权重的确定等。
[1]张少文,王文圣,丁晶,等.分形理论在水文水资源中的应用[J].水科学进展,2005,16(1):141-146.(ZHANG Shaowen,WANG Wensheng,DING Jing,et al.Application of fractal theory to hydrology and water resources[J].Advances in Water Science,2005,16(1):141-146.(in Chinese))
[2]周银军,陈立,刘欣桐,等.河床表面分形特征及其分形维数计算方法[J].华东师范大学学报:自然科学版,2009(3):170-178.(ZHOU Yinjun,CHEN Li,LIU Xintong,et al.Study on fractal properties of a river bed and the calculation method of its fractal dimension[J].JournalofEastChina NormalUniversity:Natural Sciences,2009(3):170-178.(in Chinese))
[3]陈刚,胡素端,王怡璇,等.基于GIS的泾河流域径流过程分形特征研究[J].水资源与水工程学报,2011,22(3):124-127.(CHEN Gang,HU Suduan,WANG Yixuan,et al.Research on fractal characteristics of runoff process in Jinghe River Basin based on GIS[J].Journal of Water Resources and Water Engineering,2011,22(3):124-127.(in Chinese))
[4]李扬,严宝文.渭河流域径流序列的分形特征研究[J].人民黄河,2009,31(1):25-27.(LI Yang,YAN Baowen.Study on fractal characteristics of runoff in Weihe River Basin[J].Yellow River,2009,31(1):25-27.(in Chinese))
[5]张安兵.动态变形监测数据混沌特性分析及预测模型研究[D].徐州:中国矿业大学,2009.
[6]宋立松,魏高峰.动态分维数在时间序列分析中的应用[J].浙江水利科技,2000(1):14-16.(SONG Lisong,WEI Gaofeng.Application of dynamic fractal dimension in time analysis[J].Zhejiang Hydrotechnics,2000(1):14-16.(in Chinese))
[7]石凤,张雁秋,李艳芬,等.水体富营养化的预防及治理办法[J].环境科学与管理,2008,33(2):144-147.(SHIFeng, ZHANG Yanqiu, LIYanfen, atel.Prevention and treatment methods of water eutrophication[J].Environmental Science and Management,2008,33(2):144-147.(in Chinese))
[8]胡晓镭.湖、库富营养化机理研究综述[J].水资源保护,2009,25(4):44-47.(HU Xiaolei.Summing up the research on eutrophication mechanisms of lakes and reservoirs[J].Water Resources Protection,2009,25(4):44-47.(in Chinese))
[9]詹勇,李畅游,史小红,等.分形理论在乌梁素海湖泊水质评价中的应用[J].水资源与水工程学报,2012,23(2):37-43.(ZHAN Yong, LI Changyou, SHI Xiaohong,et al.Application of fractal theory to the evaluation of water quality in Wuliangsuhai Lake[J].Journal of Water Resources& Water Engineering,2012,23(2):37-43.(in Chinese))
[10]黄晓英,李娟.基于污染损害指数法的深圳水库水质评价与分析[J].环境科学与管理,2009,34(7):178-182.(HUANG Xiaoying, LIJuan. Waterquality assessment and analysis of shenzhen reservoir based on pollution harm index method[J].Environmental Science and Management,2009,34(7):178-182.(in Chinese))
[11]赵晓亮,齐庆杰,赵国智.城市水库水质模糊综合评价模型建立与应用[J].科技导报,2012,30(11):53-56.(ZHAO Xiaoliang, QI Qinjie, ZHAO Guozhi.Establishment and applications of fuzzy comprehensive evaluation model for city drinking water source quality assessment[J].Science & Technology Review,2012,30(11):53-56.(in Chinese))
[12]汪红军,彭建华,梁开封.综合水质标识指数法在水库水质评价中的应用[J].人民长江,2007,38(1):92-94.(WANG Hongjun, PENG Jianhua, LIANG Kaifeng.Application of comprehensive water quality identification index in assessment of reservoir water quality[J].Yangtze River,2007,38(1):92-94.(in Chinese))
[13]黄健,贾克力,席北斗,等.乌梁素海富营养化的神经网络评价[J].人民黄河,2011,33(1):75-76.(HUANG Jian,JIA Keli,XI Beidou,at el.Neural network evaluation of Wuliangsuhai Lake eutrophication[J].Yellow River,2011,33(1):75-76.(in Chinese))

