基于改进型LMS自适应算法的谐波检测方法

段玉波 姜骁楠 付光杰

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

随着电力电子装置的广泛使用，电网中的谐波问题日益严重，如何准确、实时地检测电网畸变电流的谐波分量是决定有源电力滤波器补偿性能的重要环节[1，2]。目前电流检测的方法大体上可以归于频域检测和时域检测两大类。基于频域的谐波电流检测主要有快速傅里叶变换法(FFT)[3，4]和小波理论谐波检测。快速傅里叶变换法由于计算量大，会产生较大的时间延迟，动态响应较慢，因而在实际系统中不实用。小波理论谐波检测精确度高，但其运算量依然很大，还未被广泛应用。

谐波电流的时域检测方法是目前研究的重点，主要有基于瞬时无功功率理论谐波检测法和基于LMS(Least Mean Square)算法的自适应对消法[5～9]。基于瞬时无功功率的谐波检测方法中用到了数字低通滤波器，而传统的低通滤波器延时较大，直接影响检测的精确性和动态跟踪速度。自适应谐波检测方法算法简单、易于实现，对元件参数变化不敏感，在动态性能上有很大的改善空间。然而传统的固定步长自适应算法在收敛速度、跟踪速度与收敛精度方面对步长调整因子μ的要求是矛盾的。为了解决这一矛盾,覃景繁和欧阳景正提出Sigmoid函数的变步长LMS算法，有较快的跟踪速度和较小的稳态误差[10]。但是，Sigmoid函数在误差e(n)接近零时变化太大，使得该算法在接近稳态时步长变化依旧很大。针对这一问题，文献[11～15]分别给出了相应的改进算法。笔者将基于瞬时无功功率理论的谐波检测与变步长LMS自适应算法相结合，得到较快的动态响应速度与良好的检测精度。

1 基于瞬时无功功率理论的谐波检测与自适应谐波检测①

1.1 基于瞬时无功功率理论的ip-iq算法

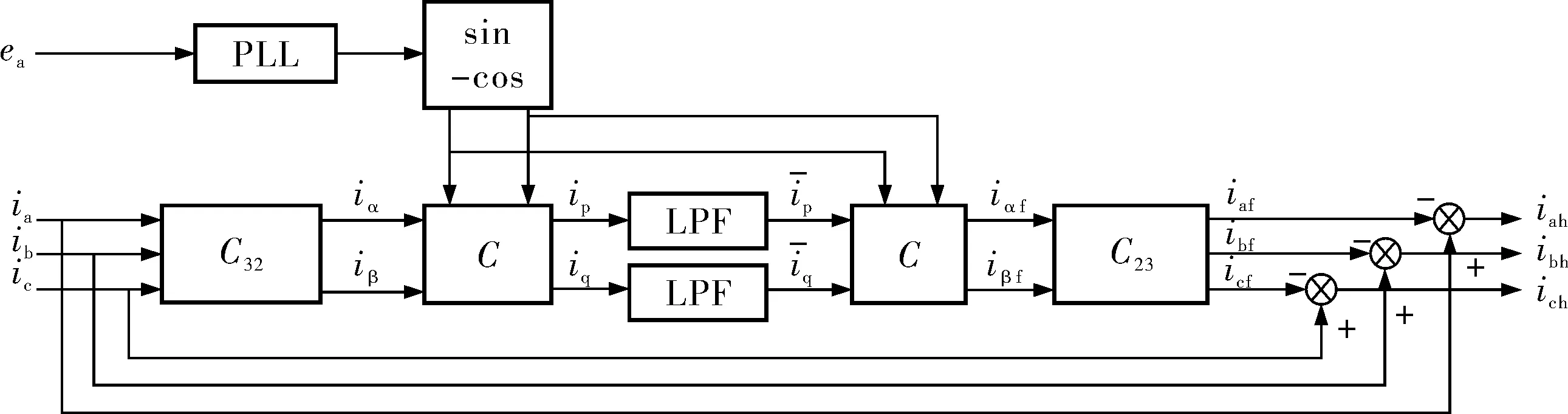
图1 基于瞬时无功功率的电流检测原理

1.2 LMS自适应算法原理

自适应谐波检测原理如图2所示。

图2 自适应谐波检测原理

图2中，输入信号矢量X(n)=[x1(n),x2(n),…,xl(n)]T，权值系数矢量W(n)=[w1(n),w2(n),…,wl(n)]T，因此滤波器的输出为：

y(n)=WT(n)X(n)

(1)

y(n)相对于滤波器期望输出信号的误差为：

e(n)=i(n)-y(n)=i(n)-WT(n)X(n)

(2)

均方误差性能函数为：

f(w)=E[e2(n)]=E{[i(n)-WT(n)X(n)]2}

(3)

f(w)对w的梯度为零，那么便可求出f(w)最小时刻的条件，即w的最佳权值wopt。但在实际应用中，为了使自适应算法更加实用化，提出一种梯度寻优的LMS近似算法，使用瞬时估值误差平方值的梯度▽we2(n)来近似均方估值误差梯度▽wE[e2(n)]，得到权值w的迭代公式：

▽we2(n)=-2e(n)X(n)

(4)

W(n+1)=W(n)+2μe(n)X(n)

(5)

其中，μ是设定步长调整因子。该算法以牺牲算法性能为代价换取运算量减少，直接后果是递推权值不会严格收敛于wopt，只是围绕wopt波动，波动程度取决于μ取值的大小。

2 改进型LMS自适应算法的谐波检测

2.1 改进型LMS自适应算法

变步长LMS算法基于这样的准则：当权值远离最佳权值wopt时，选择较大的步长以加快动态响应速度和对时变系统的跟踪速度；当权值接近最佳权值wopt时，选择较小的步长以保证检测精度。步长调整因子μ取决于瞬时误差e(n)，瞬时误差e(n)不可避免地存在噪声δ(n)，对于式(2)有：

e(n)=[Wopt-W(n)]TX(n)+δ(n)

(6)

令V(n)=Wopt-W(n)，对式(6)进行平方得到：

e2(n)=X(n)VT(n)V(n)XT(n)+δ2(n)-

2δ(n)X(n)VT(n)

(7)

对式(7)求期望，并由δ(n)和X(n)不相关，且E[δ(n)]=0可得：

E[e2(n)]=E[X(n)VT(n)V(n)XT(n)]+E[δ2(n)]

(8)

显然，由于噪声E[δ2(n)]的存在，会影响步长μ，而：

e(n)e(n-1)=δ(n)δ(n-1)-δ(n-1)[X(n)VT(n)-

δ(n)]X(n-1)VT(n-1)+X(n)VT(n)·V(n-1)XT(n-1)

(9)

E[e(n)e(n-1)]=E[X(n)VT(n)V(n-1)XT(n-1)]

(10)

利用误差自相关e(n)e(n-1)来调整步长可以有效抑制噪声。为了进一步抑制噪声干扰，引入中间变量p(n)对自相关均值估计进行表示。

笔者提出的改进型变步长LMS算法为：

(11)

p(n)=γp(n-1)+(1-γ)e(n)e(n-1)

(12)

β(n+1)=ξβ(n)+ηp2(n)

(13)

式(11)是基于双曲正切函数的变步长算法。双曲正切函数与Sigmoid函数形状相似，同时也存在误差e(n)接近零时变化太大的缺点，因此引入参数m改善函数形状，使函数底部形状平缓。图3所示为α=1，β=1时，分别令m=1和m=20时，μ的函数图象。β用来控制函数的取值范围，这里采用变量β(n)。β(n)随着p2(n)变化而变化，避免因β的固定而引起较大的稳态误差。

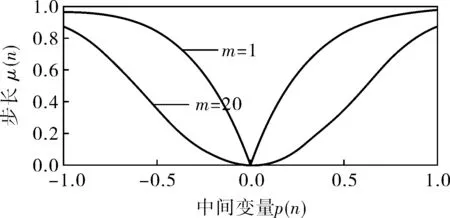
图3 μ和p(n)的关系曲线

式(12)是对误差自相关e(n)e(n-1)进行滑动指数窗运算，有：

p(n)=γp(n-1)+(1-γ)e(n)e(n-1)

(14)

令窗的宽度为N，那么可以认为在n-N+1之前的数据可以忽略，则式(12)可以表示为：

(15)

指数窗运算可以进一步地抑制噪声。在计算初始阶段，p2(n)较大，步长μ也会比较大；达到最佳权值时，p2(n)就接近于零，步长μ就会变小。

把式(15)带入式(13)有：

(16)

取期望可得：

=ξE[β(n)]+η(1-γ)2E{[e(i)e(i-

(17)

(18)

β的取值应该小于μmax，那么：

(19)

通过对η、ξ的调整，可以达到很好地动态响应。在递推过程中，对步长μ有如下约束条件：

(20)

2.2 谐波检测方法

图4 基于ip-iq运算的自适应电流检测原理

3 仿真验证

用MATLAB仿真软件进行仿真，仿真电路如图5所示。负载为三相对称非线性负载，由带阻感负载的整流桥产生，触发角为30°。L=100mH、R=10Ω、La=Lb=Lc=10mH、Ra=Rb=Rc=1Ω。

图5 仿真电路图

三相负载电流如图6所示，可以看出负载电流中含有丰富的谐波分量。

由前文的分析，设α=1、m=20、γ=0.99、ξ=0.95、η=0.001。以A相为例，通过传统的检测系统与改进型的检测系统得到的A相基波与谐波电流的检测结果对比如图7所示。从图7中看出，改进的检测系统比传统的检测系统可以更快速准确地获取电网基波，实现谐波分量的分离，跟踪性能更好，有较快的响应速度。

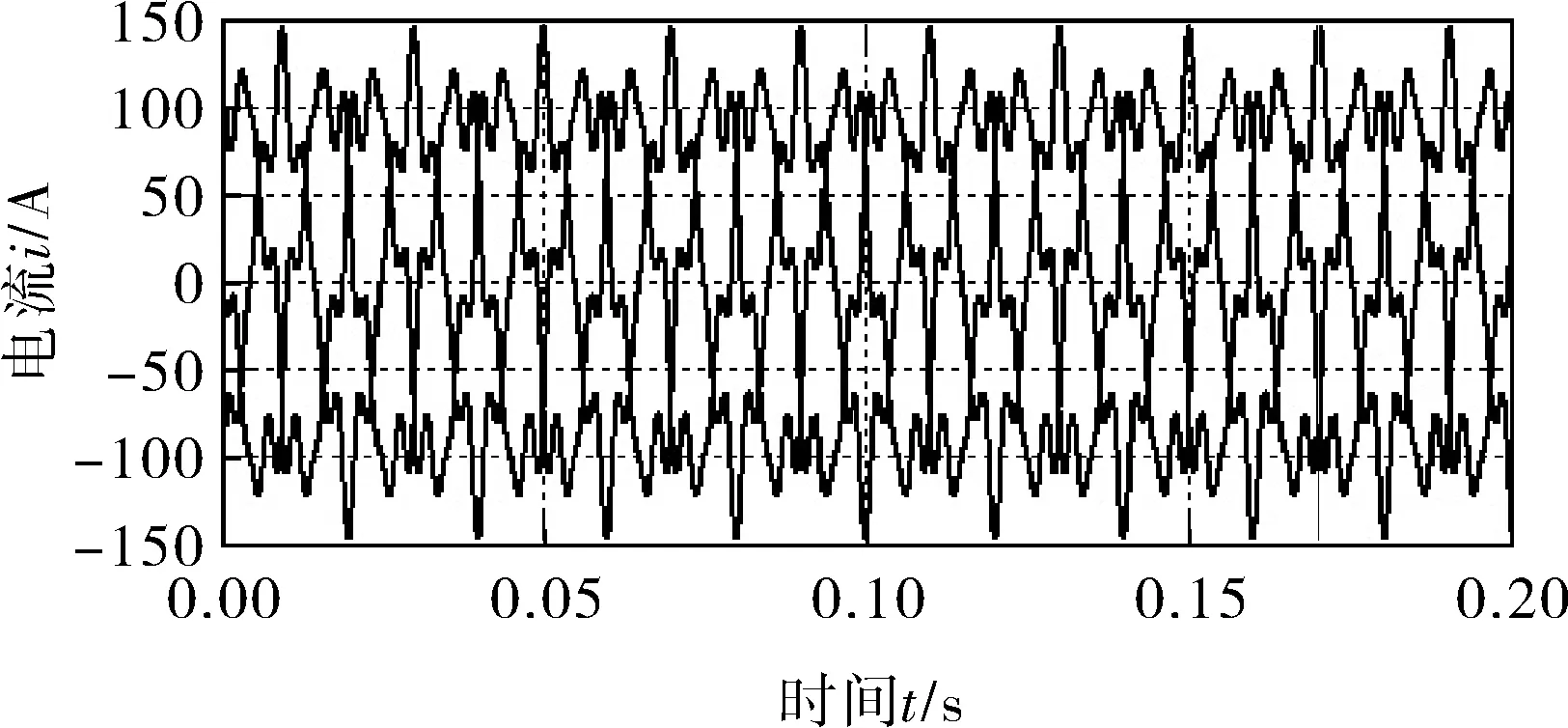
图6 三相负载电流波形

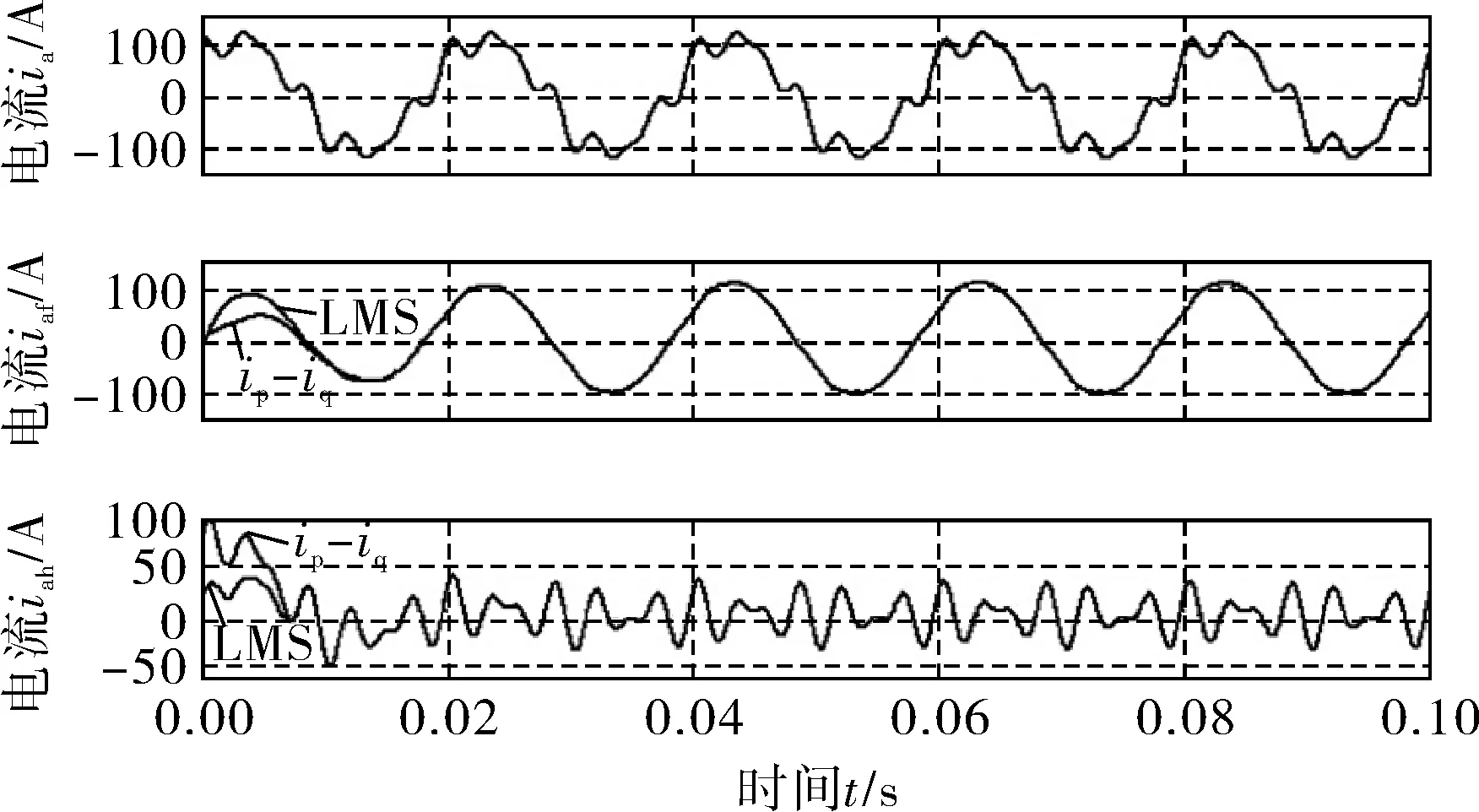
图7 A相电流检测波形

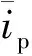
笔者还对传统的变步长算法与改进后的变步长算法的权值变化进行了比较，如图9所示。比较可见，改进型的变步长算法的权值响应更快，收敛后波动更小。

图8 直流分量检测结果

图9 两种算法权值比较结果

4 结束语

笔者采用自适应滤波器代替原来基于瞬时无功功率的检测电路中的低通滤波器(LPF)，并在此基础上对变步长LMS算法进行改进，进一步提高动态性能与检测精度。将这种检测方法应用于三相谐波的检测，经过仿真验证，改进后的方法有较好的动态性能与较高的检测精度。