混合粒子群算法求解单机批调度问题
常俊林 孟彦军 王 庆 叶 宾
(中国矿业大学信息与电气工程学院,江苏 徐州 221006)
粒子群算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法,该算法已在工业中有了广泛应用[1]。
单机调度是生产调度问题的一种特殊形式,半导体芯片的预烧、电路测试、港口货物装卸及金属加工等都属于该类型。在实际生产过程中,对于大规模的生产活动,需要进行批量处理,机器在处理工件时,可以将多个工件同时进行加工以提高生产效率,降低生产成本,这就是所谓的单机批调度问题。文献[2]首先提出了该类问题的单机器模型,即单机批调度问题,证明了该类问题的制造跨度问题是强NP问题。文献[3]求解极小化总完工时间的单机批调度问题,提出了基于工件序列的蚁群算法和基于批序列的蚁群算法。文献[4]研究了单机环境下工件尺寸有差异的批调度问题,并设计了一种改进蚁群算法对问题的制造跨度进行优化。文献[5]采用模拟退火方法求解最小化最大完工时间的单机批处理调度问题。随着单机批处理调度问题研究的深入,对于调度问题的约束条件也越来越多,工件动态到达的单机批调度问题的研究也己逐渐成为一个很有价值的研究方向。但是目前研究工件动态到达的单机批调度的文献很少[6,7],并且在生产调度问题的优化研究方面,应用智能优化算法来改进求解的质量仍存在不足。文献[8]利用分批的启发式规则产生初始种群,然后重新设计了交叉算子和变异算子以优化制造跨度。但遗传算法的求解性能依赖于种群规模,因此在解决大规模问题时收敛性能较差。文献[9]中微粒群算法在对批调度问题求解时,主要是使用工件序列对解进行编码,将改进操作放在成批阶段,对微粒群算法得到的工件序列釆用动态规划算法进行改进。上述启发式方法不能充分考虑问题的约束条件,难以找到最优解,因此,另外一些学者采用了性能更优的元启发式算法(meta-heuristic algorithm)。文献[10]提出了求解最小化最大完工时间的单机批处理调度问题的启发式算法和蚁群算法,并且考虑了工件尺寸不等和动态工件到达的约束条件。文献[11]利用蚁群聚类算法求解工件具有不同到达时间的单机批调度问题。上述算法虽然能在一定程度上有效求得问题的优化解,但是随着迭代次数的增加,算法容易陷入局部最优,降低算法的收敛速度。因此笔者提出利用混合粒子群算法来求解工件动态到达的单机批调度问题,并引入自适应策略和惯性权重正弦函数,防止算法陷入局部最优,同时也提高了算法的收敛速度。
1 数学模型①
单机批调度问题描述如下:工件到达之后,在满足机器容量Bmax和工件到达时间的约束下,可以将多个工件作为一批同时进行加工,并且只有加工时间相同的工件才可以加入同一批中,同一批工件具有相同的开始和结束加工时间。从一批开始加工直到该批加工完成,该过程不允许中断,也不允许有工件中途退出或加入该批,因为同一批中的工件由一台机器进行加工,具有共同速度,所以批加工时间由批中工件的加工时间最大的工件决定。到达时间、交货期都是已知的。
根据上述描述,所求问题的数学模型和约束条件为:
Rb=max{rj|j∈b}
(1)
Cb=Pb+Sb
(2)
Li=Cb-di
(3)
s.t.
Sb≥Rb
(4)
nb≤Bmax
(5)
Pb=max{pi}
(6)
优化目标函数为:
minLmax=max(Li)
(7)
其中,Rb、Pb、Sb、Cb分别为批b的释放时间、加工时间、开始加工时间和最大完工时间;di、ri、Ci、Li分别为工件i的交货期、释放时间、最大完工时间和最大拖期时间;Lmax为最大拖期时间;约束条件(4)表示批b的开始加工时间要大于批的到达时间,约束条件(5)表示第nb个批工件个数不超过Bmax,约束条件(6)表示批加工时间等于批中工件最大加工时间。
单机批调度问题可以分为两个过程:工件成批和批的加工。工件成批主要是对工件到达时间按升序排列后,在满足机器批容量的前提下,已到达工件中加工时间相等的工件加入一批,否则新建批。分批完成后将工件分配到批处理机进行加工,得到目标函数。
2 算法设计
2.1 标准粒子群(PSO)算法描述
基于微粒群优化算法独特的搜索机制,PSO算法首先在可行解空间和速度空间随机初始化微粒群,即确定微粒的初始位置和初始速度,通过评价各微粒的目标函数,确定t时刻每个微粒所经过的最佳位置pi和群体最佳位置pg,再按下列公式分别更新各微粒的速度和位置:
vijk+1=wvijk+c1r1(pijk-xijk)+c2r2(pgjk-xijk)
(8)
xijk+1=xijk+vijk+1
(9)
式中c1——自身经验学习因子;
c2——社会经验学习因子;
r1、r2——[0,1]之间的随机数;
w——惯性权重因子。
2.2 混合粒子群算法
由于所求调度问题是离散的,所以采用基于工件序列的编码方式可以更好地表达问题的解。为了保证编码策略不遗漏问题的全局最优解,并使优化操作满足状态的可行性和合法性,设计一种针对随机键编码的基于升序排列(ranked-order-value,ROV)的操作,用于实现从微粒的连续位置矢量到工件排序的转换。假定有6个工件的调度问题,设根据NEH启发式算法和随机方法产生粒子位置[1.9,1.8,0.7,3.5,2.4,1.2],采用ROV规则,基于升序排列得:4,3,1,6,5,2,所得排列即工件的加工序列。
在式(8)中,由于粒子速度向量vi本身具有随机性和盲目性,导致算法收敛性较差,无法快速寻找到新的解区域。在考虑实际优化问题时,求解最优解的思想就是首先通过全局搜索,快速收敛于某一新的解空间,然后采用局部搜索来获得高精度的解。惯性权重因子w是一个控制参数,不仅控制本次飞行速度对下次飞行速度的影响程度,还体现着粒子群优化算法对全局搜索与局部搜索的平衡。因此合理地选择有利于更好地平衡算法的全局搜索能力和局部搜索能力,协调算法的搜索精度和收敛速度。在迭代初期阶段,希望有较高的搜索能力以探索新的解空间跳出局部极值,而在后期则重视局部开发以加快收敛并发现精确解,通过对粒子群算法中惯性权重的分析,提出了一种惯性权重正弦调整方法来改进粒子群算法中的惯性权重[12],以改善粒子群算法的收敛速度和全局收敛性。为了防止算法陷入局部最优,在改进算法的基础上引入自适应变异全局极值的变异操作来开发算法跳出局部最优的能力[13]。
2.2.1惯性权重正弦调整
首先对由式(8)、(9)组成的系统进行稳定性分析。为便于表达,把式(8)、(9)中的问题简化为一维,记φ1=c1r1,φ2=c2r2,则粒子i的运动状态方程为:
vik+1=wvik+φ1(pik-xik)+φ2(pgk-xik)
(10)
xik+1=xik+vik+1
(11)
根据文献[14]所得结论可知:
-(φ1+φ2)xik=vik+1-wvik-φ1pik-φ2pgk
(12)
对式(8)~(10)化简,可知粒子的速度变化过程是一个二阶差分方程:
vik+2-(1+w-φ1-φ2)vik+1-wvik=0
(13)
粒子的位置变化过程也是一个二阶差分方程。将粒子速度变化过程看成是一个时间连续过程,对时间求导得到一个典型的二阶差分方程:
(14)
其中e1、e2为方程λ2+(φ1+φ2-1-w)λ+w=0的根。根据式(14)解的一般形式可知,当粒子的速度趋向无穷大时,粒子的运动轨迹是发散的,导致整个粒子群的运动轨迹是发散的,粒子速度变化过程的稳定性对整个粒子群行为有着重要影响。假定φ1、φ2为常数,那么式(13)z变换后的系统方程则可看成是一个线性系统,其特征方程为:
z2+z(φ1+φ2-1-w)+w=0
(15)
对式(15)作双线性变换,将z=(μ+1)/(μ-1)代入式(15)化简得:
(φ1+φ2)μ2+(2-2w)μ+2(2w+2-φ1-φ2)=0
(16)
特征方程的所有零点均在z平面上一个以原点为圆心的单位圆内,这是二阶线性系统稳定的必要条件。由罗斯判据可知二阶线性系统稳定的充要条件是特征方程各项系数均为正值,可得式(13)稳定的条件为:
(17)
由于φ1、φ2为正实数,所以在不考虑随机量且个体最优值、全局最优值位置不变的情况下,单个粒子速度变化过程稳定的条件由式(17)的后两个不定式决定,且两个条件不能同时取等号,满足条件时单个粒子的速度将趋向于0。用同样的方法对粒子位置变化过程进行分析,得到粒子位置变化过程稳定的条件:
(18)
较大的w值有利于跳出局部最优,进行全局寻优;较小的w值有利于局部寻优,加速算法收敛。笔者提出一种正弦调整的粒子群算法惯性权重:
w(k)=0.4+0.5sin(πk/maxgen)
(19)
令φ1=[w(k)+1]r1,φ2=[w(k)+1](2-r1)r2,r1、r2为均匀分布在(0,1)区间的随机数,式(17)、(18)所有条件均可得到满足,从理论上说明了粒子群算法的收敛性能。由正弦变化规律可知w值的变化对算法的影响,在算法开始时粒子在其自身附近作局部寻优,在一定时期后粒子的搜索范围逐渐增大,进行全局寻优,最后让最优粒子进行局部搜索。
2.2.2自适应变异全局最优值
如果粒子群优化算法陷入早熟收敛或者达到全局收敛,粒子群中的粒子就会聚集在搜索空间的一个或几个特定位置,群体适应度方差σ2等于零。设粒子群的粒子数目为n,fi为第i个粒子的适应度,favg为粒子群目前的平均适应度,根据适应度函数,适应度方差定义为:
(20)
其中f是归一化定标因子,其作用是限制σ2的大小。令:
(21)
由于粒子在当前全局最优值gBest的作用下可能发现更好的位置,因此新算法将变异操作设计成一个随机算子,即对满足变异条件的gBest按一定的概率pm变异。pm的计算公式如下:
(22)
其中,k=rand(0.1,0.3);σd2的取值与实际问题有关,一般远小于σ2的最大值;fd可以设置为理论最优值。
对于gBest的变异操作,算法中采用增加随机扰动的方法,η是服从Gauss(0,1)分布的随机变量,gBest的第k维全局极值变异公式为:
gBestk=gBestk(1+0.5η)
(23)
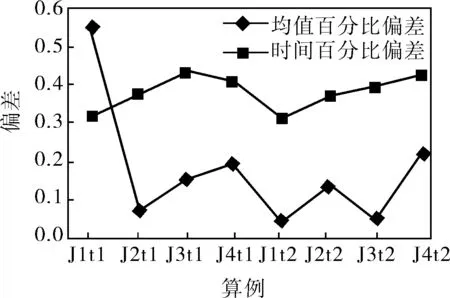
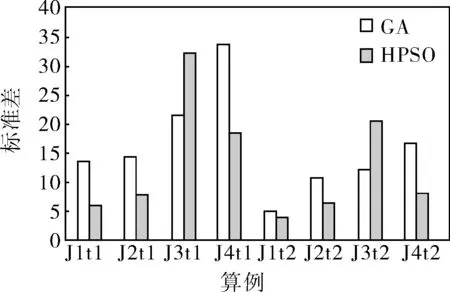
首先判断算法是否满足收敛准则,如果不满足,对粒子进行位置和速度的更新,判断此时粒子适应度值是否满足fi 为了验证改进算法的性能,实验中随机产生测试算例,其中机器容量为3;工件数J[i]分别为20、50、100、150;加工时间服从t1=[0,20]、t2=[0,10]均匀分布;设置参数α和β分别用来控制工件的释放时间分布和交货期分布的松紧程度,其值分别为0.2和3;算法中最大迭代次数和种群规模都为100;w、v和x的取值范围分别为[0.40,0.91]、[-4,4]和[0,4];函数unifrnd(0,a)取(0,a)之间的随机数,ri=unifrnd(0,αCmax),di=ri+unifrnd(1,β)pi,这里暂不讨论参数对算法的影响。 笔者将遗传算法(GA)与提出HPSO算法进行比较,运行在Windows XP系统、CPU E6600 3.06GHz、内存1.96G的台式电脑上。所有算法采用Matlab编程,每种算例运行30次。笔者对运行结果和运行时间从最差值、最优值、平均值及百分比偏差(百分比偏差=(L(HPSO)-L(GA))/L(GA))等方面进行比较,比较结果见表1、2。 表1 两种算法运行结果的比较 表2 两种算法运行时间的比较 从表1、2中可以看出,HPSO算法要明显优于GA算法,随着问题规模的增大,HPSO算法的解与GA算法的差距更为明显,显示了很好的稳定性。在运行时间上,HPSO算法在所有算例上的求解时间均小于GA算法,随着问题规模的增大相对GA算法有着更快的收敛速度。为了更直观地看出算法的性能优劣,分别用折线图和条形图描述了算法均值百分比偏差和标准差的分布情况(图1、2)。 图1 运算结果均值和运行时间百分比偏差 图2 标准差值的分布 由图1可知,HPSO算法相对GA算法有一定的改进,但对于J1t1算例均值百分比偏差出现不稳定的状态,对于大部分算例是随着问题规模的增大效果越明显,而且两种不同加工时间下相比较,改进比较稳定。对于运行时间的改进则表明,随着问题规模的增大,改进效果越明显,表现在算例中则是收敛速度变大。总体来说HPSO算法更能适应复杂的调度环境。 由图2可以看出,除了算例J3t1和J3t2的标准差出现波动外,HPSO算法的标准差均比GA算法的小,表明HPSO算法的寻优能力比GA算法寻优能力强,能够跳出局部最优区域。标准差表明组内算例间的离散程度,也就是算例结果偏离平均值的程度,同时反映数据波动范围大小,能不能在有限的迭代次数内寻到最优值。由此可知,HPSO算法所得数据波动范围较小,更适合对此类调度问题分析。 笔者提出了一种基于工件动态到达求解批调度问题最大拖期时间的改进粒子群算法(HPSO)。该算法在标准PSO算法的基础上引入了改进的惯性权重正弦调整,改善了算法的收敛速度和全局收敛性。为了防止算法陷入局部最优并增强粒子群优化算法跳出局部最优解的能力,在改进惯性权重算法的基础上引入自适应变异全局极值的变异操作来寻找全局最优解。采取工件序列对应粒子位置的编码方式,通过实验表明,在求解基于工件动态到达的单机批调度问题上,无论从寻优能力还是运行时间方面,HPSO算法的性能要优于GA算法性能。笔者应用改进算法求解的是单机调度问题,对于应用此算法求解基于工件动态到达的多机批调度问题还有待进一步研究。3 实验设计与仿真


4 结束语

