双模圆锥喇叭天线的设计∗

丁晓磊， 徐 磊

(北京遥测技术研究所 北京 100076)

双模圆锥喇叭天线的设计∗

丁晓磊， 徐 磊

(北京遥测技术研究所 北京 100076)

双模圆锥喇叭通过TE11模和TM11模的适当综合，获取轴对称的等化波束方向图和低的交叉极化电平。由于双模圆锥喇叭具有结构简单的突出优点，对于窄频带的反射面天线系统，它是替代波纹圆锥喇叭的理想馈源方案。

双模； 圆锥喇叭； 轴对称方向图

引 言

主模圆锥喇叭因其口径场分布的特点决定了辐射方向图的E面比H面窄且副瓣较高，无法达到等化要求。而波纹喇叭虽然具有频带宽、交叉极化低、波束等化性能好的优点，但由于其结构复杂，增大了加工难度和加工成本。双模圆锥喇叭[1～5]尽管频带窄，但具有结构简单、口径效率高的突出优点。对于窄频带的反射面天线，若要求馈源方向图具有低副瓣、低交叉极化和轴对称的等化波束，双模圆锥喇叭是一种优选方案。

1 双模圆锥喇叭的设计

双模圆锥喇叭通过引进一个高次模TM11模来改善E面方向图，使其方向图具有轴对称的等化波束特性。由于双模圆锥喇叭的结构实现形式不是唯一的，下面结合设计实例介绍两种实现方案。图1是圆波导中主模TE11模和高次模TM11的口径电场分布及其合成后的口径场分布示意图。

为产生图1所示的口径场分布，可以采用图2所示的双模喇叭结构形式。图2(a)是1963年由Potter P D提出的双模圆锥喇叭，也叫Potter喇叭。图2(b)是省略圆柱双模移相段的双模圆锥喇叭，也称为Pickett-Potter喇叭。两种喇叭的工作原理都是通过调整r2/r1的比值获得满足要求的模式幅度比；调整移相段的长度l和喇叭长度h(对于图2(b)只调整喇叭长度h)，使两种模式到达口径面的相位相等，最终获得图1所示的合成效果。

对于主模传输段，为保证传输主模TE11的同时抑制其他高次模，r1的取值范围为1.84＜kr1＜3.83。对于圆柱双模移相段或省略移相段结构的台阶突变截面，为保证传输主模TE11模和高次模TM11的同时抑制其他高次模，r2的取值范围为3.83＜kr2＜5.33。由于结构的轴对称性，在截面突变处m ＞1的高次模TEmn或TMmn模将无法激励传输。

图1 圆波导中主模TE11模、高次模TM11的口径场分布

图2 双模圆锥喇叭结构示意图

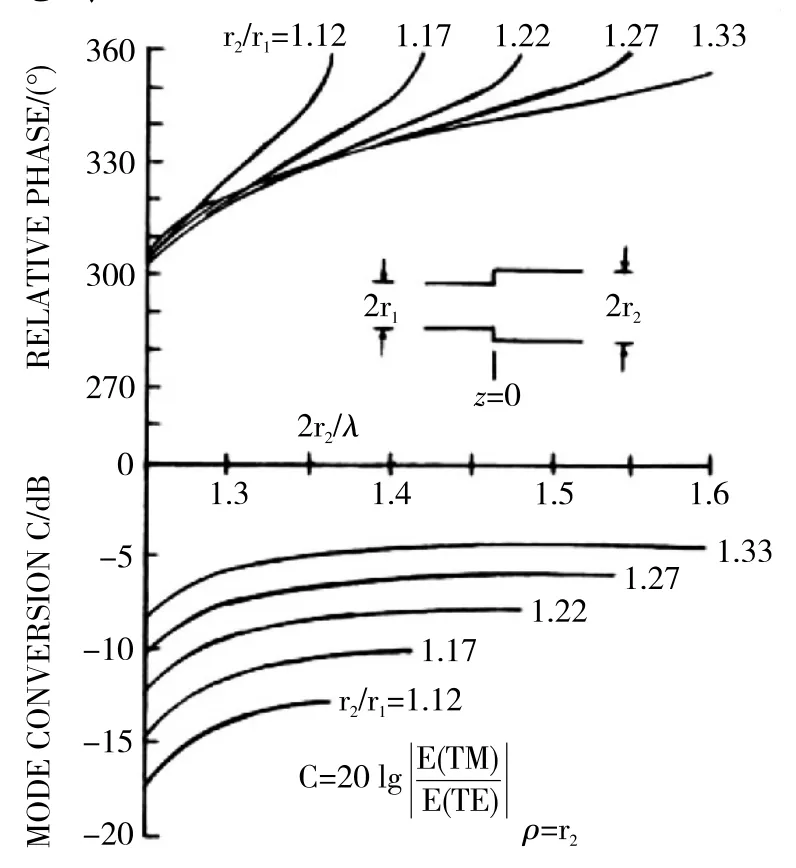
图3 圆波导截面突变处的模式转换系数和TM11模相对于TE11模的相位差

1.1 Potter喇叭的设计

图3是双模圆波导截面变化处的模式变换因子和TM11模相对于TE11模的相位差。该图是设计Potter喇叭天线的关键依据。

选定喇叭参数后，当相位关系满足式(1)时，即可实现等化波束的设计。

式中，φex是截面突变处TM11模相对于TE11模的相位差，其取值可参考图3读取；φph是圆波导双模移相段的相位差，式(1a)是其计算公式；φfl是喇叭段的相位差，式(1b)是其计算公式。

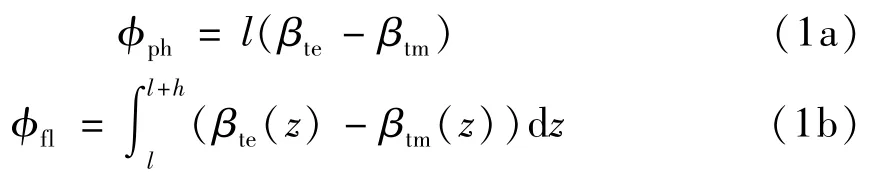
对于图2(a)的喇叭设计，其步骤可归纳为以下几步。

①根据增益和波束宽度要求，参考圆锥喇叭的设计公式选择喇叭口径半径b；

②根据r1、r2的取值范围和r2/r1的比值约为1.3的原则，选取r1、r2的值；

③根据图3读取截面突变处TM11模相对于TE11模的相位差φex的值；

④取l＝λTE11/4，根据式(1)计算喇叭长度h，λTE11是移相段中TE11模的波导波长；

⑤采用HFSS电磁仿真软件，建模仿真喇叭的电性能。由于满足式(1)的l和h值不是唯一的，具体数值可根据增益最大或喇叭长度最短的原则，微调l和h的值，得到满足要求的Potter喇叭天线。

图4是本文设计的Ku频段Potter喇叭的仿真结果。喇叭参数为r1＝0.54λ，r2＝0.72λ，r2/r1＝1.3，l＝λTE11/4，h＝5.2λ，λ是中心频率对应的工作波长，喇叭总长为5.85λ。

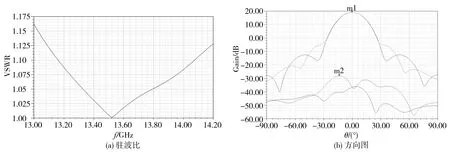
图4 Ku频段Potter喇叭仿真结果

1.2 Pickett-Potter喇叭的设计

Pickett-Potter喇叭是圆柱双模移相段的长度为零的双模圆锥喇叭。图5是文献[5]给出的Pickett-Potter喇叭的设计图。在确定r1、r2、b的取值之后，喇叭长度参数h可以直接从图中读取。

文献[5]还给出了最优喇叭参数对应的增益值、波束宽度及交叉极化性能。

图6是设计好的Ku频段Pickett-Potter喇叭的仿真结果。喇叭参数为r1＝0.5λ，r2＝0.68λ，h＝5.52λ，λ是中心频率对应的工作波长，喇叭总长为5.83λ。和Potter喇叭的长度相比可知，两种喇叭的长度基本相同。

图5 Pickett-Potter喇叭最优参数

2 结束语

比较两种结构双模圆锥喇叭的设计方法可知，无移相段的双模喇叭的设计图表参数全面，设计方法简单，而且该种结构的喇叭加工也相对简单一些。在波束宽度相同的情况下，两种喇叭的长度基本相同。综合双模圆锥喇叭的设计方法、加工工艺、天线参数和天线性能可知，对于窄频带的反射面天线馈源，若要求馈源方向图具有低副瓣、低交叉极化和轴对称的等化波束，无移相段的双模圆锥喇叭是一种优选方案。

图6 Ku频段Pickett-Potter喇叭仿真结果

[1]Potter PD.A New Horn Antenna with Suppressed Sidelobes and Equal Beamwidths[J].Microwave Journal，6，June 1963：7178.

[2]林昌禄.天线工程手册[M].北京：电子工业出版社，2002：551～558.

[3]Volakis JL.Antenna Engineering Handbook[M].fourth edition.The McGraw.Hiu Companies，2007：469.

[4]秋 实，高红卫，焦永昌，等.E面和H面方向图等化的双模圆锥喇叭设计[J].强激光与粒子束，2005，17(8)：1235～1238.

[5]Skobelev S P，Ku Bon-Jun，Shishlovt A V，and Ahn Do-Seob.Optimum Geometry and Performance of a Dual-mode Horn Modification[J].Antennas and Propagation Magazine，IEEE，43(1)：99～93.

Design of Dual M ode Conical Horn

Ding Xiaolei， Xu Lei

A dual-mode horn with the proper combination of the circular TE11and TM11modes has a highly symmetrical radiation pattern and a relatively low cross-polarization level.Because of the advantage of the simple structure，dual-mode horns are thus often used as substitutes for corrugated horns in a narrow frequency for a reflector antenna.

Dualmode； Conical horn； Beam axial symmetry

TL503

A

CN11-1780(2014)06-0013-03

丁晓磊 1971年生，博士，研究员，主要研究方向为天线理论与技术。

总装预研项目

2014-05-12

徐 磊 1979年生，硕士，高级工程师，主要研究方向为反射面天线。