基于粒子群脊波神经网络的飞机目标识别
谷志刚,孙锋利
(1.空军大连通信士官学校, 辽宁 大连 430074;2.空军石家庄飞行学院,河北 石家庄 050081)
0 引言
多尺度几何分析是高维(图像)信号处理与分析领域中非常重要的技术和手段之一,其中脊波理论[1]是多尺度几何分析中发展较早和较为成熟的技术之一.受小波神经网络的启发,脊波理论与神经网络结合产生的脊波神经网络[2-7](Ridgelet Neural Network,RNN)不仅具有小波网络的尺度和位置通道,还具有方向性,这使得脊波神经网络更适于处理高维奇异性(线奇异、面奇异),构造出更为复杂的决策面,从而获得性能更为优良的网络模型;因此,脊波神经网络在函数拟合与估计、模式识别、系统辨识、奇异检测等领域具有很好的应用前景.脊波神经网络的自由参数包含线性突触权值和非线性的脊波参数(尺度、位置和方向),这使得网络的学习训练过程变得复杂.传统文献[2-7]中多采用基于梯度下降的网络学习算法,在学习网络的非线性参数时,需要进行较为复杂的梯度运算,网络收敛速度慢,尤其是当特征空间维数较高时,网络学习效率大为降低,所以要达到预定学习精度需要更多隐层神经元和更长时间,而且算法可调参数少,网络不易控制,算法后期容易出现震荡.本文提出一种粒子群脊波神经网络训练算法,由于不需要梯度运算,而且通过控制粒子群的惯性系数、种群规模、学习因子、速度和位置界等,可实现网络快速有效的学习,得到了性能更好、规模更小的网络模型.
1 脊波神经网络模型及梯度训练算法
1.1 脊波神经网络模型
脊波神经网络模型是基于脊波重建公式而建立的一种新的神经网络模型,是多尺度几何分析技术与神经网络模型相结合的产物.根据脊波理论[1],定义:
定义1称
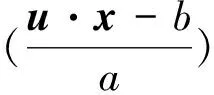
(1)
为由满足容许性条件的ψ(·)产生的脊波函数,其中:γ∈Γ,空间Γ={γ=(a,u,b),a,b∈R,a>0,u∈Sd-1,‖u‖=1},Sd-1为d维空间的单位球面;a为尺度参数;b为位置参数;u为方向参数.
从(1)式可以看出,脊波函数会在尺度、位置和方向3个通道产生相应的变化效应,相对于小波处理一维点奇异性的优点,公式(1)在处理高维奇异性方面极为有利.根据定义1,文献[1]给出了如下的重构定理:
定理1任何f∈L1∩L2(Rn)的函数可以由满足(1)、(2)的脊波函数重构,即
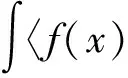
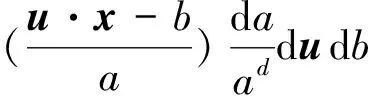
(2)
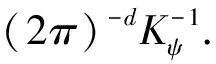
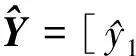
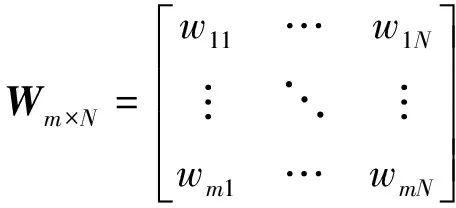
隐层激活函数为一族脊波函数,表示为ψ((uj·xi-bj)/aj),j=1,…,N, 其中:aj,bj∈R,aj>0,uj∈Rd, ‖uj‖=1.为公式简洁起见,本文用矩阵来表示方向、尺度和位置参数[5],即
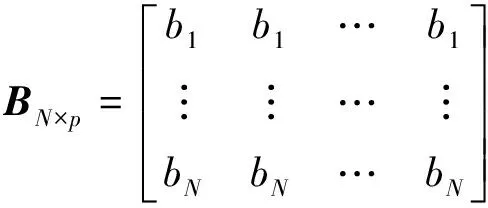
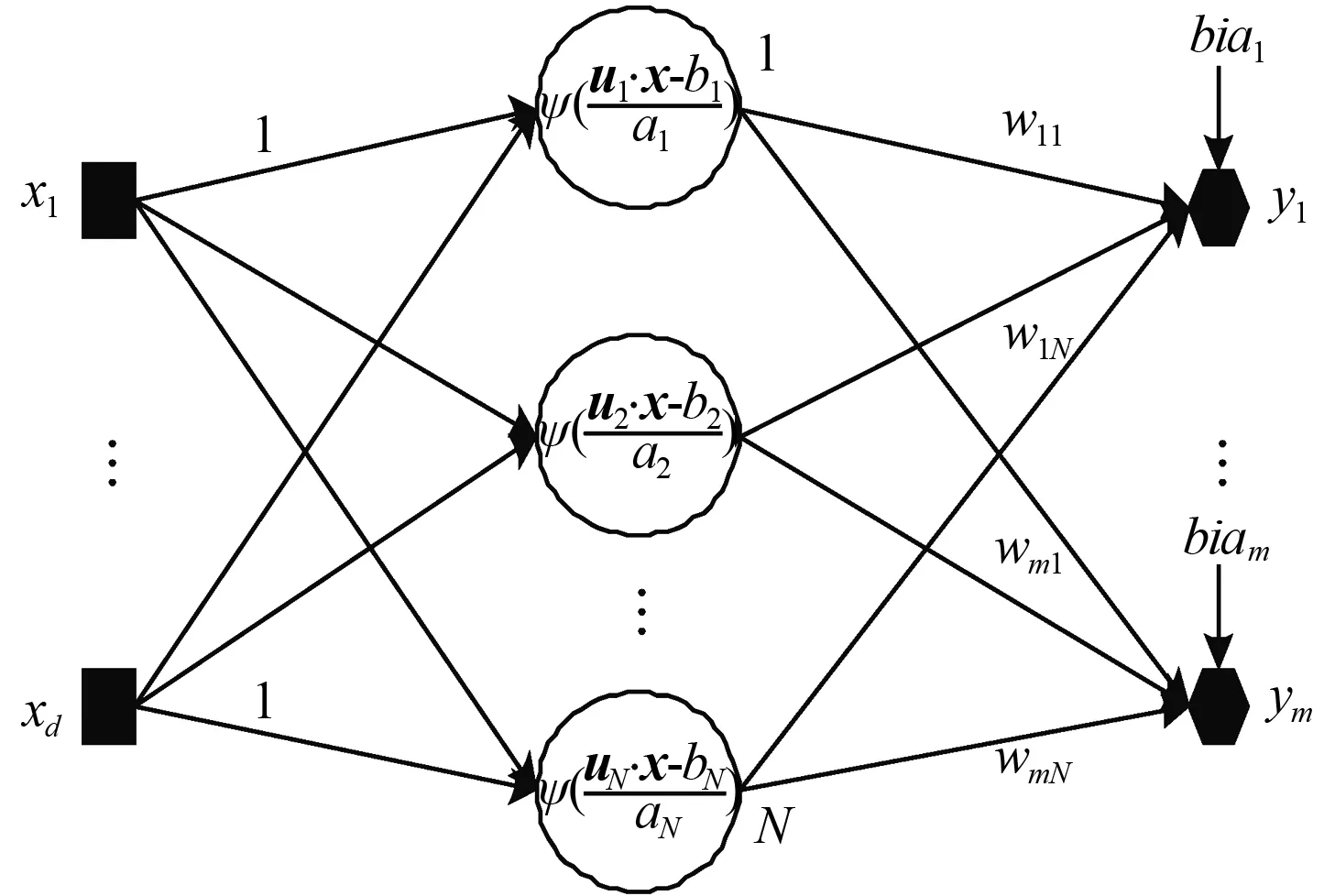
图1 单隐层脊波神经网络模型
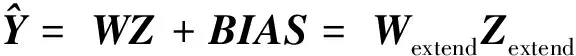
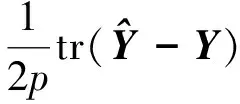
(3)
其中tr(·)为矩阵的迹.
1.2 脊波神经网络的梯度下降算法
梯度下降算法是神经网络学习的经典算法,尽管它存在收敛慢,容易陷入局部极值,后期容易震荡等不足,但是对于(3)式的性能函数它能提供一个基本稳定和可靠的收敛性能.在实际工程应用中,梯度下降算法对工程应用的影响并不太大,尤其是一些离线学习场合,因此本文依然选择梯度下降算法作为学习算法(算法详细过程参见文献[7]).算法中各个参数虽然可以采用相同的学习率,但根据本文作者对大量数据的试验表明,对线性的权值参数采用较小的学习率,而对非线性的脊波参数采用较大的学习率将有利于提高学习效率,算法收敛较快;因此,在实际中可以根据具体问题采用两个或多个学习率实现网络的学习.
2 脊波网络的粒子群训练算法
为了避免脊波网络的梯度学习算法中存在的不足问题,根据脊波网络学习中线性和非线性参数并存的特点,提出一种脊波网络的粒子群学习算法,该算法将传统的粒子群算法与脊波网络的特点相结合.其主要特点有:①对线性权值和偏置参数采用随种群进化线性减小的惯性因子,而非线性脊波参数的惯性因子采用固定值;②限制粒子的飞行速度、脊波函数的尺度和位置参数界,从而实现对脊波激励函数分辨力的控制;③引入变异操作,增加了种群多样性,避免了早熟.关于粒子群算法的基本原理可参考文献[8-10].粒子群脊波神经网络学习算法流程可描述如下:
1) 种群初始化.包括种群规模、最大进化代数、自学习及社会学习因子、尺度和位置及方向参数惯性权重因子;为了提高算法的效率,对网络权值和偏置解空间范围进行了限制,脊波方向参数范围必须取[-1,1],各粒子初始速度取0,并对最大速度进行限制;设定训练目标误差及变异概率;网络各参数初始化为小随机矩阵.
种群初始化过程:
%种群规模及进化最大代数、自学习和社会学习因子
swarm_size=N,itermax=G;c1=λ;c2=γ;
%网络权值和偏置的惯性权重因子的上下界
ωwmax,ωwmin;ωbiasmax,ωbiasmin;
%尺度、位置和方向参数的惯性权重因子
ωa=ωb=ωu=constant;
%网络权值和偏置解空间范围
weights=[startw,endw],bias=[startbias,endbias];
%脊波尺度和位置解空间范围,方向参数范围是[-1,1]
scale=[starta,enda],location=[startb,endb];
%最大速度限制
V_limit=Vmax;
%训练目标误差、变异概率
Erro_goal=E;mutation=pro;
For each bird
初始化粒子个体的网络权值、偏置、尺度、位置和方向参数为解空间范围内的小随机矩阵;初始化粒子个体的各参数速度为0;
%个体历史最优适应度初始值
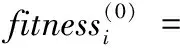
End
fitness_global(0)=∞;%社会历史最优适应度初始值
2) 种群进化.以训练误差函数作为种群进化适应度函数,计算每个粒子的适应度值,求出个体最优和社会最优适应度值,若社会最优适应度值达到目标误差时即结束进化,若未达到则对粒子的位置和速度进行更新.
种群进化过程:
k=1; %k代表进化代数
Do
For each bird
%计算每个粒子的当前适应度值,D=5
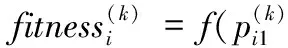
更新个体历史最优位置为当前位置;
End
End
%社会最优适应度
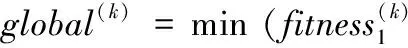
Iffitness_global(k)≤E, Return; End
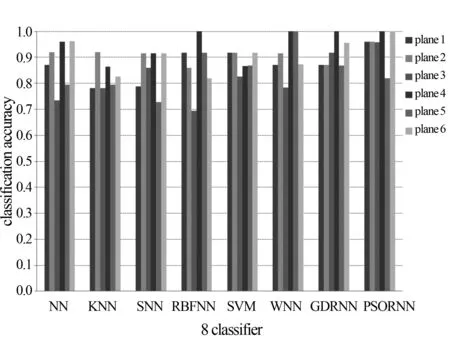
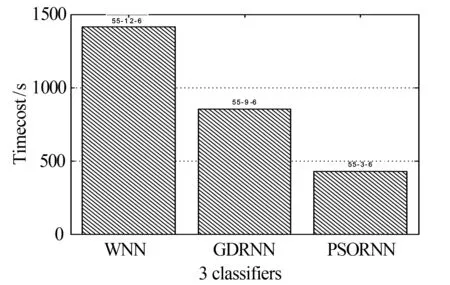
Iffitness_global(k) %更新当前社会最优适应度值 fitness_global(k)=fitness_global(k); End %更新个参数社会最优位置,j代表第几个参数 For each bird, each parameter 3) 位置变异.根据变异概率对粒子的位置进行变异操作. %粒子位置变异 %速度和位置限制 End k=k+1; End (while (k 4) 返回第2步. 由于本文中的粒子群学习算法对粒子的位置引入了变异操作,这在一定程度上避免了种群早熟的现象,使网络学习可以逃离局部极值点,进而提高了粒子群学习算法的精度,这对网络的学习效率和网络结构都会产生有利的效果,最终可以获得精度更高、速度更快和结构更简单的脊波神经网络模型. 为了验证网络和学习算法的有效性,将粒子群脊波神经网络(PSORNN,Particle Swarm Optimized Ridgelet Neural Network)用于6类飞机目标的识别,每类有标准、残缺、旋转等38幅飞机图像,共计228幅.随机取40%图像(共90幅)作为训练样本,其余作为测试样本,提取每幅图像的10阶55维Pseudo-Zernike矩特征,特征提取采用外接圆法,使用文献[11]中的快速算法实现,部分试验图像如图2所示. 图2 6类飞机目标的部分图像样本 脊波神经网络的隐层神经元数目采用文献[4]中的逐渐递增的方式确定,初始隐层神经元数为1,最终确定隐层神经元数为3,网络最终结构为55-3-6,网络目标误差为0.01;粒子群学习算法进化代数为2 000代,种群规模为100,自学习和社会学习因子为1.427 9,网络线性权值和网络偏置范围分别为weights=[-∞,∞]和bias=[-∞,∞],脊波参数解空间范围scale=[0.1,10],location=[-2,2],方向参数为单位向量,所以其范围为[-1,1];非线性脊波参数和线性权值及偏置速度均限制为[-1,1],网络权值和偏置惯性因子采用线性递减策略,范围为[0.4,0.9],脊波参数惯性因子均为0.725. 为了说明网络的性能优势,将粒子群脊波神经网络的分类性能与传统的最近邻分类器(NN,Nearest Neighborhood)、K近邻分类器(K-NN)、壳最近邻分类器[12](SNN,Shelly-Nearest Neighborhood)、径向基神经网络(RBFNN,Radia Basis Feed-forward Neural Network)、支撑向量机(SVM,Support Vector Machine)、小波神经网络(WNN,Wavelet Neural Network)及梯度下降法训练的脊波神经网络(GDRNN,Gradient Descendent Ridgelet Neural Network)进行比较,比较结果如表1和图3所示.图4为小波神经网络、梯度下降法训练的脊波神经网络和粒子群脊波神经网络的网络结构和训练时间比较. 实验基于Intel 2.0GHz双核处理器,支撑向量机采用台湾林智仁教授的LibSVM version 2.87软件包(http://www.csie.ntu.edu.tw/~cjlin/),其他分类器算法编程均基于Matlab7.0神经网络工具箱函数和计算平台. 表1 PSORNN与传统分类器的总体分类精度 图3 PSORNN与传统分类器对各类目标的分类精度比较 图4 3种网络的结构及训练时间代价(柱状图上的数字为网络结构) 1) PSORNN与传统分类器相比,其推广能力得到一定提高.从表1看出,各分类器对训练样本的分类精度均达到百分之百,而PSORNN分类器的测试精度相比之下提高约3%;由图3可以看出,PSORNN对各类飞机目标的识别率明显高于其他分类器.这主要是由于脊波基函数具有尺度、位置和方向3个通道,能够充分利用特征空间的高维奇异性,同时由于隐层采用多个不同尺度、位置和方向的脊波激励函数,因而可以构造出更为复杂的分类曲面,从而提高了分类精度. 2) 从神经网络角度看,PSORNN分类器的训练时间短,网络规模小.在实际的数值试验中,图4中的3种网络隐层神经元数目均采用逐步递增的方式确定,其中:WNN最终采用55-12-6的网络结构,经过了25 000步梯度下降法学习;GDRNN最终采用55-9-6的网络结构,经过15 000步梯度下降法学习;PSORNN最终采用55-3-6的网络结构,经过2 000代进化学习,且其时间消耗仅为425.6 s,比前两种神经网络大约减少2/3的学习时间.PSORNN具有以上优点的主要原因在于样本的分类信息不仅存储在网络权值中,而且存储在脊波参数中,这使得网络不需要太多的网络权值数目即可达到一定的分类精度,加之PSO算法快速的全局搜索能力,使PSORNN具有较小的规模和较高的学习效率. 3) PSORNN网络可调参数比GDRNN增多,通过优化和调整相关参数,如种群规模、进化代数、惯性因子、学习因子等可以在相同的网络结构下一定程度地改善性能,并且由于PSO算法自身所具有的特点,不会使网络出现震荡,因而性能相对稳定,网络可控性增强. 本文采用的粒子群算法克服了传统文献采用的基于梯度的方法的不足,使网络的训练变得更为简单和直接,提高了训练的精度和效率,获得了规模更小的网络模型,因此具有一定的工程应用价值.脊波神经网络等多尺度几何分析网络是神经网络发展的一个很有潜力的方向,其与深度学习理论、量子理论、遗传算法、免疫算法等先进理论和算法的结合,依然有很多值得研究的内容. 参考文献: [1] Candès E J. Ridgelets:theory and applications[D]. USA:Department of Statistics, Stanford University, 1998. [2] 杨淑媛,焦李成,王敏.一种自适应脊波网络模型[J].西安电子科技大学学报:自然科学版,2005,32(6):890-894. [3] 杨淑媛,焦李成,王敏.一种新的方向多分辨脊波网络[J].西安电子科技大学学报:自然科学版,2006,33(4):557-562. [4] Yang Shuyuan,Wang Ming,Jiao Licheng. Incremental constructive ridgelet neural network[J]. Neurocomputing,2008,72:367-377. [5] Amjady N, Keynia F, Zareipour H. Short-term wind power forecasting using ridgelet neural network[J]. Electric Power Systems Research, 2011,81(12):2099-2107. [6] Zheng N, Tan H F. SAR image classification based on brushlet and self-adaptive ridgelet neural network[J]. Applied Mechanics and Materials, 2013,347:3024-3028. [7] 孙锋利,何明一,高全华.基于自适应脊波网络的高光谱遥感图像分类[J].计算机科学,2011,38(8):260-264. [8] Kennedy J, Eberhart R C. Particle swarm optimization[J]. IEEE Conference on Neural Networks, 1995:1942-1948. [9] Eberhart R C, Kennedy J. A new optimizer using particle swarm theory[J]. Institute of Electrical and Electronics Engineers, 1995,10:39-43. [10] Shi Y, Eberhart R C. A modified particle swarm optimizer[J]. Institute of Electrical and Electronics Engineers, 1998,5:69-73. [11] 夏婷,周卫平,李松毅,等.一种新的Pseudo-Zernike矩的快速算法[J].电子学报,2005,33(7):1295-1298. [12] 钟智,朱曼龙,张晨,等.最近邻分类方法的研究[J].计算机科学与探索,2011,5(5):467-473.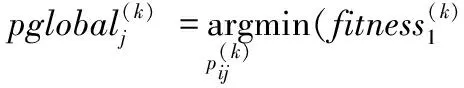
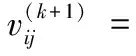
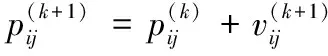
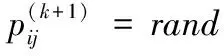
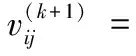
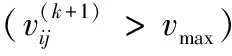
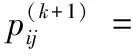
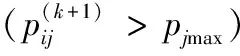
3 实验及结果分析
3.1 6类飞机目标的分类试验


3.2 试验结果分析
4 结束语

