On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables
WU Yong-feng
(Department of Mathematics and Computer Science,Tongling University,Tongling 244000,China; Center for Financial Engineering and School of Mathematical Sciences,Soochow University,Suzhou 215006,China)
On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables
WU Yong-feng
(Department of Mathematics and Computer Science,Tongling University,Tongling 244000,China; Center for Financial Engineering and School of Mathematical Sciences,Soochow University,Suzhou 215006,China)
In this article,the author establishes the strong laws for linear statistics that are weighted sums of a m-negatively associated(m-NA)random sample.The obtained results extend and improve the result of Qiu and Yang in[1]to m-NA random variables.
Marcinkiewicz-Zygmund strong law;complete convergence;weighted sums; m-negatively associated random variable
§1.Introduction
The concept of negatively associated(NA)was introduced by Joag-Dev and Proschan[2].
Def i nition 1.1A f i nite family of random variables{Xk,1≤k≤n}is said to be NA if for any disjoint subsets A and B of{1,2,···,n}and any real coordinate-wise nondecreasing functions f on RAand g on RB,

whenever the covariance exists.An inf i nite family of random variables is NA if every f i nite subfamily is NA.
Hu et al[3]introduced the following concept of m-negatively associated(m-NA).
Def i nition 1.2Let m≥1 be a f i xed integer.A sequence of random variables{Xn,n≥1} is said to be m-NA if for any n≥2 and any i1,···,insuch that|ik−ij|≥m for all 1≤k/= j≤n,Xi1,···,Xinare NA.
We now provide two examples of sequences of m-NA random variables.
Example 1.1Let{Xn,n≥1}be a sequence of NA random variables and let m≥2. For n≥1,let r≥1 be such that(r−1)m+1≤n≤rm and let Zn=Xr.Then{Zn,n≥1} is a sequence of m-NA random variables.
Example 1.2Let{Xn,n≥1}be a sequence of NA random variables and let{Yij,i≥1,1≤j≤m−1}be an array of independent random variables which is independent of {Xn,n≥1}.Let m≥2.For n≥1,let r≥1 be such that(r−1)m+1≤n≤rm and let
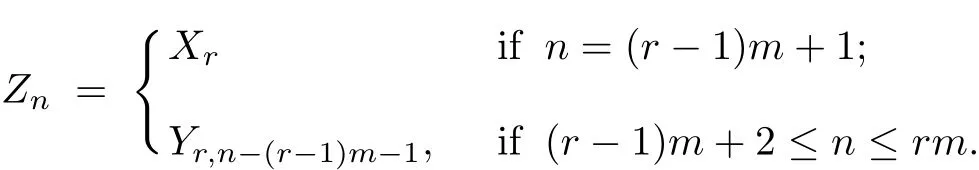
Then{Zn,n≥1}is a sequence of m-NA random variables.
Let{X,Xn,n≥1}be a sequence of random variables and{ani,1≤i≤n,n≥1}be a triangular array of constants.Because the weightedare very important in some linear statistics,the strong convergence for the weighted sums has been studied by many authors(see[1,4-12]).
The concept of the complete convergence was introduced by Hsu and Robbins[13].A sequence of random variables{Un,n≥1}is said to converge completely to a constant θ if

In view of the Borel-Cantelli lemma,the above result implies that Un→θ almost surely. Therefore,the complete convergence is a very important tool in establishing almost sure convergence of summation of random variables as well as weighted sums of random variables.
Recently Qiu and Yang[1]studied the following Marcinkiewicz-Zygmund strong law.
Theorem ASuppose 1/p=1/α+1/β for 1<α,β<∞and 1<p<2.Let{X,Xn,n≥1}be a sequence of NA random variables with indentical distributions,and let{ani,1≤i≤n,n≥1}be an array of constants satisfying

If E|X|β<∞and EX=0,then

The purpose of this article is to establish the complete convergence and the Marcinkiewicz-Zygmund strong laws for linear statistics of m-NA sequences of random variables.The obtained results extend and improve the result of Qiu and Yang[1].It is worthy to point out that we obtain the complete convergence result for weighted sums of m-NA random variables under the same conditions of Qiu and Yang[1].
Throughout this paper,the symbol C represents positive constants whose values may change from one place to another.
§2.Preliminaries
A sequence of random variables{Xn,n≥1}is said to be stochastically dominated by a random variable X(write{Xn}≺X)if there exists a constant C>0 such that

Lemma 2.1Nondecreasing functions def i ned on disjoint subsets of a set of m-NA random variables are m-NA.
Lemma 2.2[1416]Let{Xk,k≥1}be a sequence of NA random variables,EXk=0, E|Xk|q<∞for some q≥2 and for every k≥1.Then there exists C=C(q)depending only on q,such that
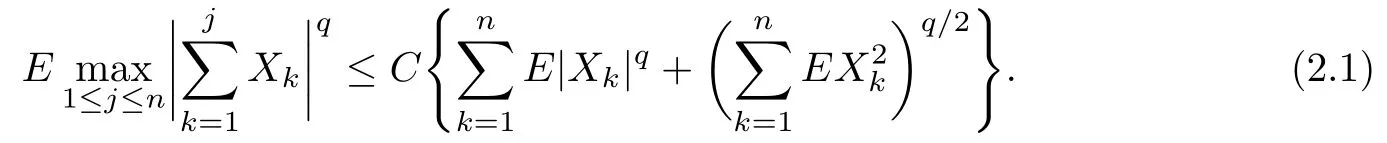
Lemma 2.3Let{Xk,k≥1}be a sequence of m-NA random variables,EXk=0, E|Xk|q<∞for some q≥2 and for every k≥1.Then there exists C=C(q,m)depending only on q and m,such that(2.1)remains true.
ProofIf n≤m,obviously{Xn,n≥1}is a sequence of NA random variables.Therefore,Def i ne



Lemma 2.4Let{Xn,n≥1}be a sequence of random variables with{Xn}≺X.Then there exists a constant C such that,for all q>0 and x>0
(i)E|Xk|qI(|Xk|≤x)≤C{E|X|qI(|X|≤x)+xqP(|X|>x)};
(ii)E|Xk|qI(|Xk|>x)≤CE|X|qI(|X|>x).
§3.Main Results
Theorem 3.1Suppose 1/p=1/α+1/β for 1<α,β<∞and 1<p<2.Let {Xn,n≥1}be a sequence of m-NA random variables with EXn=0 and{Xn}≺X and let {ani,1≤i≤n,n≥1}be an array of constants satisfying(1.1).If E|X|β<∞,then
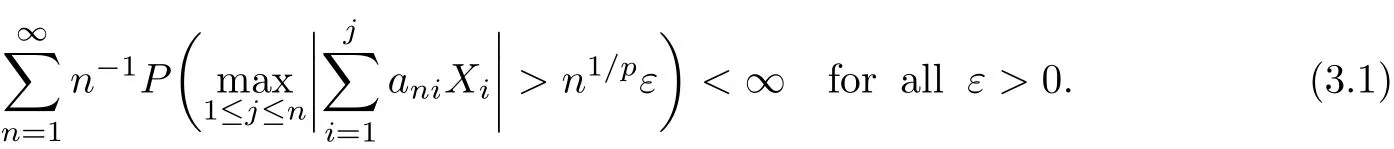
Corollary 3.1Under the conditions of Theorem 3.1,(1.2)holds.
Remark 3.1Corollary 3.1 generalizes the result of Qiu and Yang[1]to m-NA random variables.From the proof of Corollary 3.1,we will fi nd that(3.1)implies(1.2).Therefore, Theorem 3.1 extends and improves Theorem A.
Proof of Theorem 3.1Without loss of generality,we may assume that ani≥0.For fi xed n≥1,de fi ne
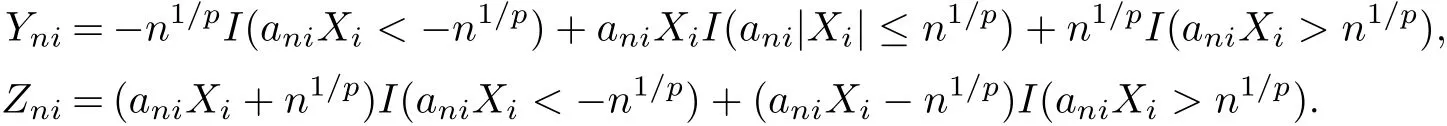
Then Yni+Zni=aniXiand{Yni,i≥1,n≥1}and{Zni,i≥1,n≥1}are both m-NA by Lemma 2.1.Then

From(1.1),without loss of generality,we may assume thatNoting that E|X|β<Then by 1/p=1/α+1/β,we have
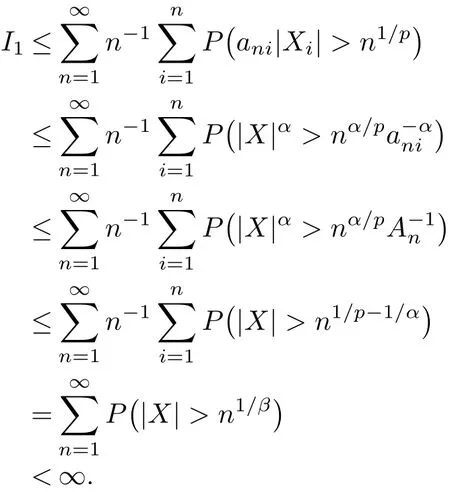
Next we prove I2<∞.We f i rst show that


It is easily seen that|Zni|≤ani|Xi|I(ani|Xi|>n1/p).By EXn=0,1/p=1/α+1/β and E|X|β<∞,we get

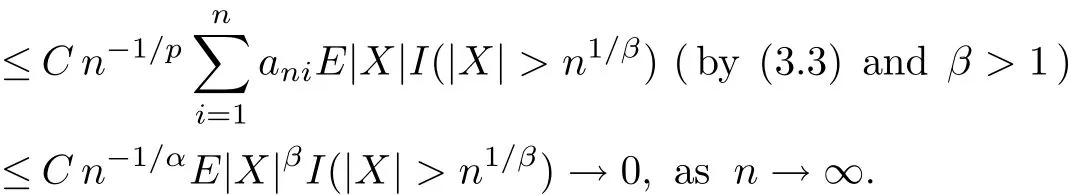
From(3.2),it follows that while n is sufficiently large,<n1/pε/2.Let q>max{α,β,2}.Then by the Markov inequality and Lemma 2.3,it follows that


By Lemma 2.4,we have
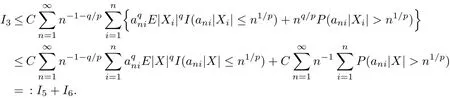
By a similar argument as in the proof of I1<∞,we can get I6<∞.Then we prove I5<∞. If β≥α,by q>β and(3.4),we have

If β<α,by q>β,β>p and(3.3),we have


Then we prove I4<∞.By Lemma 2.4 and q>2,we have

Similar to the proof of I1<∞,we have

Hence,while n is sufficiently large,<1 holds.Thus by a similar argument as in the proof of I1<∞,we can get

Finally we prove I7<∞.From 1/p=1/α+1/β and 1<p<2,we know that α≤2 and β≤2 can not hold simultaneously.Hence we need only to consider the following three cases.
Case 1α<2≤β.
By(3.4)and 1/p=1/α+1/β,we have

Case 2α≥2,β≥2.
By(3.3)and p<2,we have
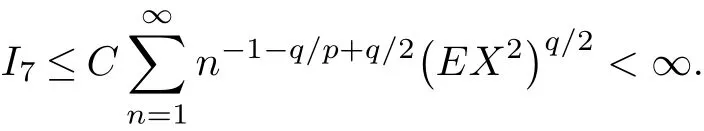
Case 3α≥2,1<β<2.
By(3.3)and β>p,we have


The proof is completed.

By the Borel-Cantelli Lemma,we get

For all positive integers n,there exists a positive integer k0such that 2k0−1≤n<2k0.By (3.5),we have

Hence,we prove that(1.2)holds.The proof is completed.
[References]
[1]QIU De-hua,YANG Xiang-qun.Strong laws of large numbers for weighted sums of identically distributed NA random variables[J].J Math Research Exposition,2006,26(4):778-784(in Chinese).
[2]JOAG D K,PROSCHAN F.Negative association of random variables with applications[J].Ann Statist, 1983,11(1):286-295.
[3]HU Yi-jun,MING Rui-xing,YANG Wen-quan.Large deviations and moderate deviations for m-negatively associated random variables[J].Acta Math Sci,2007,27B(4):886-896.
[4]CUZICK J.A strong law for weighted sums of i.i.d.random variables[J].J Theor Probab,1995,8(3): 625-641.
[5]WU Wei-biao.On the strong convergence of a weighted sum[J].Statist Probab Lett,1999,44(1):19-22.
[6]SUNG S H.Strong laws for weighted sums of i.i.d.random variables[J].Statist Probab Lett,2001,52(4): 413-419.
[7]CAI Guang-hui.Strong laws for weighted sums of NA random variables[J].Metrika,2008,68(3):323-331.
[8]WU Qun-ying.Complete convergence for weighted sums of sequences of negatively dependent random variables[J].J Probab Stat,2011,Article ID:202015.
[9]ZAREI H,JABBARI H.Complete convergence of weighted sums under negative dependence[J].Stat Papers, 2011,52(2):413-418.
[10]SUNG S H.On the strong convergence for weighted sums of random variables[J].Stat Papers,2011,52(2): 447-454.
[11]ZHOU Xin-cai,TAN Chang-chun,LIN Jin-guan.On the strong laws for weighted sums of ρ∗-mixing random variables[J].J Inequal Appl,doi:10.1155/2011/157816.
[12]SHEN Ai-ting.On the strong convergence rate for weighted sums of arrays of rowwise negatively orthant dependent random variables[J].Rev R Acad Cienc Exactas Fs Nat,Ser(A)Mat(RACSAM),doi:10.1007/s13398-012-0067-5.
[13]HSU P L,ROBBINS H.Complete convergence and the law of large numbers[J].Proc Nat Acad Sciences, 1947,33(2):25-31.
[14]SU Chun,ZHAO Lin-cheng,WANG Yue-bao.Moment inequalities and week convergence for negatively associated sequences[J].Sci China,1997,40A(2):172-182.
[15]SHAO Qi-man.A comparison theorem on maximum inequalities between negatively associated and independent random variables[J].J Theor Probab,2000,13(2):343-356.
[16]YANG Shan-chao.Moment inequalities for the partial sums of random variables[J].Sci China,2001,44A(1): 1-6.
tion:60F15
CLC number:O211.4Document code:A
1002–0462(2014)02–0265–09
date:2012-11-26
Supported by the Humanities and Social Sciences Foundation for the Youth Scholars of Ministry of Education of China(12YJCZH217);Supported by the Natural Science Foundation of Anhui Province(1308085MA03);Supported by the Key Natural Science Foundation of Educational Committe of Anhui Province(KJ2014A255)
Biography:WU Yong-feng(1977-),male,native of Zhongyang,Anhui,an associate professor of Tongling University,M.S.D.,engages in probability limit theory.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Some Results of a Certain Odd Perfect Number
- Outer P(ρ,σ)-set’s Random Characteristic and Application
- Biserial Incidence Algebras
- Bicriteria Scheduling on a Series-Batching Machine to Minimize Makespan and Total Weighted Completion Time with Equal Length Job
- Characterizing C6+P2-graphic Sequences
- Properties for Certain Subclasses of Analytic Functions Associated with Generalized Multiplier Transformation
