新型海上风电维护船的横摇运动分析

董能超，陈 悦，朱佳欢，余洋喆

(江苏科技大学船舶与海洋工程学院，江苏 镇江212003)

新型海上风电维护船的横摇运动分析

董能超，陈 悦，朱佳欢，余洋喆

(江苏科技大学船舶与海洋工程学院，江苏 镇江212003)

以从事海上风电场维护的某新型双体船的船模为试验对象，考虑维护船工作海域一般为近海，选取较小倾角进行静水横摇衰减试验，得出船模随时间变化而变化的六自由度数值及衰减曲线。通过求取减幅曲线和阻尼系数以及船模的横摇周期，对比普通相似船的经验数值，得到该双体船在静水横摇方面优良性良，也体现了船型设计的合理性，为以后海上风电维护船的船型设计提供一些参考。

风能；双体船；横摇；船模试验

0 引言

由于海上风电场主要集中在近海，因此海上风电场的维护船应具有快速性、可操作性和耐波性等优点，而双体船能较好的满足上述要求。

对于快速性和耐波性有较高要求的双体船，通常采用穿浪型双体船和小水线面型双体船。所谓小水线面双体船，是由潜没在水中的鱼类状下体、高于水面的平台(上体)和穿越水面连接上下体的支柱三部分组成。其优点是水线面面积小，受波浪干扰力较小，具有优越的耐波性；穿浪型双体船是从高速双体船发展而来，具有良好的适航性。

作为海上风电场的维护船，如采用小水线面型双体船，则舱室设备布置困难；如采用穿浪型双体船，建造难度大、造价高。为此，考虑维护船性能需要，拟采用长球首球尾船型。

1 双体维护船的实验模型和实验内容

双体船水动力分析的方法主要有数值模拟和模型试验2种,本文采用模型试验法进行分析。

1.1 实验模型

本次实验选用按照设计图纸制作的一艘新型双体船作为实验模型，实体图如图1所示。

其主尺度参数：

船长

2.10 m

垂线间长

1.90 m

型宽

0.78 m

型深

0.21 m

设计吃水

0.11 m

片体宽度

0.21 m

中心距离

0.57 m

方形系数

0.4

图1 新型双体船的实体模型

1.2 实验内容

实验内容为新型海上风电场维护船(新型双体船)的静水横摇实验。

(1)船模放入水中添加压载使船模吃水达到设计吃水。

(2)将船模放在远离岸壁的水池中，对横荡、纵荡和首摇加以约束。

(3)摆放好实验设备，将传感器固定在船模上，调整设备视角和软件初始坐标。

(4)船模初始角度7°，记录实验数据。

2 数据处理

船模横倾初始角为7°，减幅曲线为曲线，故不能按线性关系处理。

假定船模初始倾角为ΦA0进行自由横摇，第n次横摇幅值为ΦAn，相隔半个周期下一个幅值为ΦA(n+1)，则相邻二次幅值差为:

ΔΦA=ΦAn-ΦA(n+1)

(1)

相邻二次的平均幅值为：

ΦAm=0.5(ΦAn+ΦA(n+1))

(2)

以ΦAm为横坐标，ΔΦA为纵坐标即可绘制出减幅曲线。

设衰减关系目标函数为:

(3)

式中：m、n为衰减次数；a、b为线性回归系数。

用最小二乘回归分析法求得，衰减系数μ可表示为：

(4)

3 实验结果及分析

3.1 减幅曲线

根据实验所得船模的衰减曲线用excel表格法绘制出船模的减幅曲线，如图2所示。由衰减曲线可以算出船模横摇周期TΦ=1.05 s。

图2 实验所得衰减曲线

由衰减曲线量取峰值点值，计算绘制减幅曲线。半个周期的幅值平均值及最小幅值见表1，减幅曲线如图3所示。表1中，ΦAi和ΦA(i+1)分别是半个周期中的第1和第2个峰值，ΦAm为半个周期幅值的平均值，ΔΦ为半个周期中的第2个峰值。

3.2 衰减系数

应用最小二乘回归法求出a和b。因X坐标取与计算值重合坐标，误差主要来自Y，方程

(5)

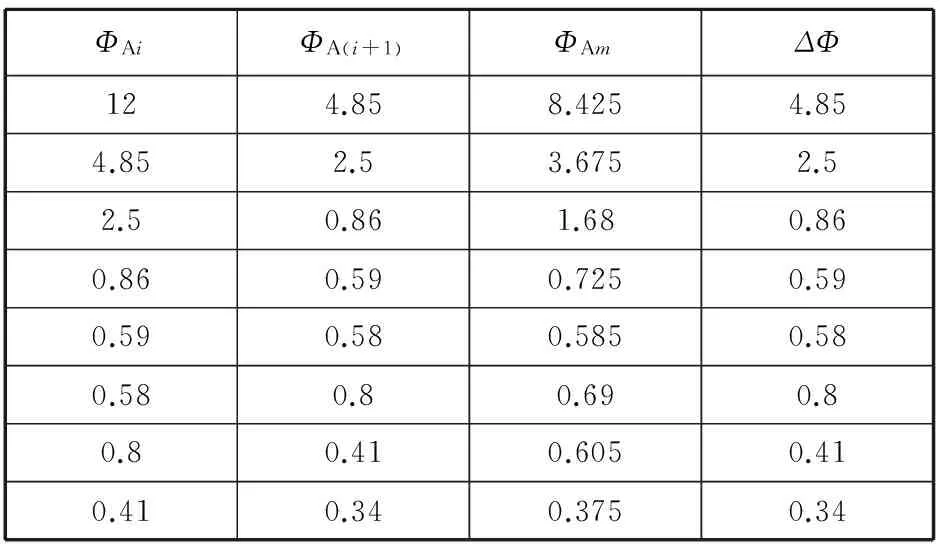
表1 半个周期的幅值平均值及最小幅值计算

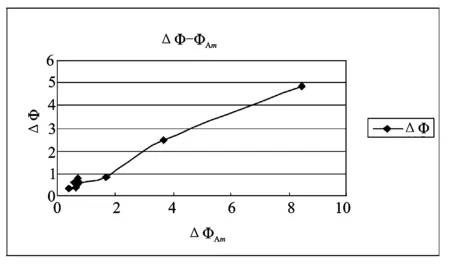
图3 减幅曲线

对a和b分别求偏导数，并令其等于零, 从而解得：

a=0.065，b=0.018 2。

ΦAm=8.425,对应衰减系数μ=0.069。

无因次衰减系数μ是表征横摇性能重要参数，自由横摇的衰减随衰减系数的增大而加快，且船舶在规则波中的频率响应函数会越小。从实验数据处理得出，本船衰减系数在初始角为7°时达到0.069，比已发表资料中表明的无舭龙骨船的0.035～0.05高出至少38%，充分表明了该新型双体维护船在横摇性能方面的优良性。

4 结论

通过对某海上风电维护船的船模进行静水横摇试验，选取初始角为7°，得到了船模自由衰减的曲线，并利用所得到的衰减曲线计算得出船模的减幅曲线和衰减系数。对比现有发表的资料船的衰减系数，得出了这种新型双体船在横摇方面具有的优良性，从而为类似船型设计提供一些参考。

[1] 盛振邦，刘应中.船舶原理[M].上海：上海交通大学出版社,2004.

[2] 赵智萍，周江华，倪海鸥，包雄关.双体船及其衍生船型[J].水运工程,2002,(11)：17-19.

[3] 郑明.两型最新的小水线面双体船[J].国防工业技术经济信息,1999,(8):16-20.

[4] 宋国华.双体船的总体性能设计[J].船舶,1998,7(2):29-32.

[5] 赵群，柴福莉.海上风力发电的现状与发展趋势[J].机电工程，2009,(12):10-12.

[6] 盛万安，程贯一.横摇非线性方程的研究[J].水动力学研究与进展，1993,(2):152-158.

[7] 姚迪，卢晓平，王毅.三体船横摇模型试验及其特性分析[J].中国舰船研究,2010,(4):6-11.

[8] JCG/Z 010-96，船舶倾斜试验与静水横摇试验实施指南[S].

[9] 彭英声.船舶非线性横摇阻尼试验测定[J].海军工程学院学报，1982，(2):10-28.

2013-11-27

董能超(1991-)，男，本科，主要从事船舶与海洋结构物性能研究；陈悦(1979-)，女，讲师，主要从事船舶与海洋结构物设计制造；朱佳欢(1992-)，男，本科，船舶与海洋工程专业；余洋喆(1992-)，女，本科，船舶与海洋工程专业。

U661.73

A