基于系统聚类分析法的铁路隧道围岩分级方法优化研究

闫 明

(铁道第三勘察设计院集团有限公司，天津 300142)

基于系统聚类分析法的铁路隧道围岩分级方法优化研究

闫 明

(铁道第三勘察设计院集团有限公司，天津 300142)

引入系统聚类分析方法，依据影响围岩工程性质的主导因素及次主导因素，对东北地区某隧道围岩分级结果进行优化，提高隧道分级的针对性。

铁路隧道 围岩分级优化 系统聚类分析 主导因素 次主导因素

隧道围岩分级是隧道支护设计与施工方案选择的重要依据，基于其对工程实际的重要影响，各国学者提出了多种隧道围岩分类方法，如前苏联的f值分级，美国的太沙基分级，美国Deere提出的按RQD值划分岩体质量的分级，挪威的巴顿以岩石质量指标Q的分级以及国内广泛采用的BQ分级等[1]。近年来，各种新的理论被引入到隧道围岩分类中，如周翠英等[2]应用神经网络法对隧道围岩进行分级，史秀志等[3]建立了隧道围岩分级的未确知均值聚类模型，张庆飞等[4]对灰色聚类理论在隧道围岩分级中的应用进行了研究。

目前，国内外使用的隧道围岩分级方法大多属于稳定性等级的划分方法，是根据大量隧道工程实例的统计分析而形成的经验性分级方法。现行《铁路工程地质勘察规范》(TB10012—2007)中所使用的围岩分级方法就是其中之一。依据规范，首先由岩石坚硬程度和岩体完整程度两项指标对围岩进行基本分级，之后再根据地下水状态和初始地应力等因素进行修正。这种方法在实际使用中虽然可以大范围的应用，但对于某个具体案例则失去了针对性，可能出现同一级别岩段的工程特性差异较大的情况。而实际工作中仅参照其所属级别进行设计施工，不能突出影响岩段工程性质的主导因素。因此，需要对上述围岩分级方法进行优化，更加突显不同岩段的工程特性。

隧道围岩分级的实质就是将相似性较大的几段围岩划归为一类的过程，而这正是系统聚类分析方法的中心思想，可以将系统聚类分析方法引入到铁路隧道围岩分级中，根据对各段围岩的系统聚类分析，了解不同围岩段的工程性质并明确它们的相互关系，最终将具有相同影响因素的岩段归为一类。

1 系统聚类分析理论及方法

聚类分析是一种多元分析方法，它直接比较各事物之间的性质，将性质相近的归为一类，将性质相差较大的归入不同的类。聚类分析方法根据分类对象的不同可以分为两类：一类是对样本所做的分类，称为Q型聚类；另一类是对变量所做的分类，称为R型聚类。聚类分析的基本思想是依据相应的定义将已知的样本或变量分为若干类，分类的过程是一个类别逐渐减少直至归为一类的过程。

系统聚类分析方法是一种对样本进行分类的方法，属于Q型聚类，该方法的基本思想是：距离较近的样本先聚成类，距离较远的后聚成类，这个过程一直进行下去，最终每个样本总能聚到合适的类中。它可以提供多种数据处理方法，在实际中应用广泛。聚类步骤主要有以下四步：

①将n个样本各作为一类。

②计算n个样本两两之间的距离。

③选定聚类方法，将距离最近的两类合并为一个新类。

④计算新类与其他各类之间的距离，再进行合并，直至只剩一类为止。

在Q型聚类分析中，首先要通过计算样本相互之间的距离来度量其相似程度，若一个样本中包含p个指标，各个指标分别代表了该样本的不同特性，则该样本可被视为一个p维向量，同时建立了一个p维空间。此时任意n个样本就成为了该空间里的n个点，而判断两个样本是否相似时，就可用代表不同样本的两点之间距离来表现相似程度。常用的距离计算方法主要有欧式距离、欧式平方距离、马氏距离以及兰氏距离等。

确定样本间距离计算方法之后还要选定类间距离的计算方法，也即聚类方法。一个类可能由单个或多个样本组成，为了比较不同类的相似程度就要求确定一种合理的算法，常用的类间距离定义有8种，分别为最近距离法、最远距离法、中间距离法、重心法、类平均法、可变类平均法、可变法和离差平方和法，与之对应的系统聚类方法也有8种。

样本间距离的选取是进行系统聚类分析的基础，而聚类方法的选择能够对聚类结果产生实质性的影响，实际选用时要考虑两者的协调性。

2 工程实例

2.1 工程概况

本次选择的工程实例是东北地区某条岩质隧道，隧道长度1 670 m。该隧道所在区域为熔岩台地与火山群区，海拔高度480～520 m，相对高差80～130 m。整体地势由南向北逐渐降低，区域构造主要为北东向及北北东向，山区冲沟发育，隧道轴线走向与山岭近垂直。

隧道穿越部位出露地层主要为太古鞍山群杨家店组变质岩系及后期侵入的脉岩和第四系松散堆积层，主体岩石类型为混合花岗岩及角闪斜长条痕状混合岩，脉岩为花岗伟晶岩和灰绿玢岩。

2.2 样本及变量的选取

在研究段落中共选取15个样本，其围岩分级情况见表1。

变量的选取过程中即参考各类已有的分级方法，又考虑了所用指标的代表性、易测性及准确性，最终选定岩石单轴饱和抗压强度(Rc)、岩体完整性系数(Kv)、渗水情况、节理分布情况等四项指标作为变量。各变量的量化方法如下。

表1 研究选取样本围岩分级情况

(1)岩石单轴饱和抗压强度(Rc)，取实测值，单位为MPa。

(2)岩体完整性系数(Kv)，取计算值。

(3)渗水情况，考虑到取样段洞身所在深度岩体多较完整，围岩多为弱透水岩体，若出水状况为干燥或湿润时取0，若出水状况为偶有渗水时取10，若出水状况为经常渗水时则取20。

(4)节理分布情况：①当统计得到的主要节理走向与洞轴线方向夹角大于45°时取5，②走向与洞轴线方向夹角小于45°、倾角小于45°时取10，③走向与洞轴线方向夹角小于45°、倾角大于45°时取20。对于②、③情况若主要节理大于5条/m2时，取值乘以2。

根据上述量化方法计算后，所选样本的各项变量数据如表2所示。

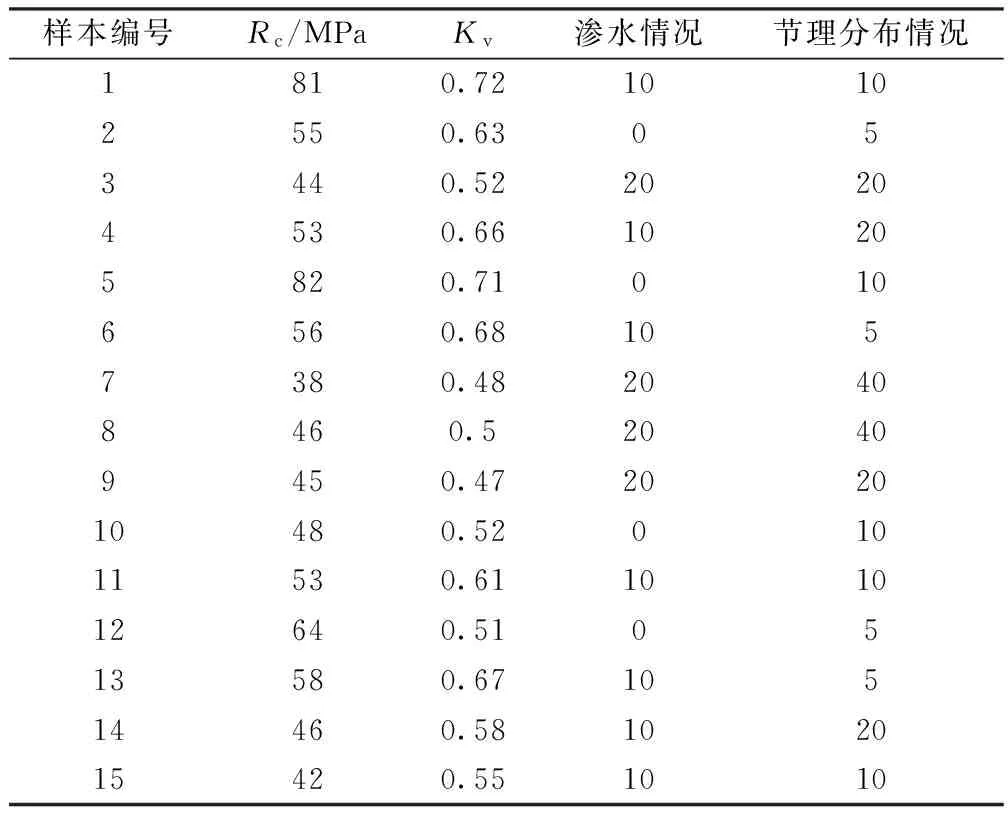
表2 所选样本各项变量取值表

2.3 系统聚类分析及其结果分析

依据以上数据，采用SPSS多元统计分析软件对各样本进行系统聚类分析。

首先，对数据进行标准化。在针对具体数据进行使用时首先要考虑的是数据标准化，因为所选取的指标量纲不同，在计算类的距离时会产生较大的偏差，所以需要对数据进行标准化处理，

然后，定义样本之间的距离为欧氏距离平方(Squared Euclidian distance)。同时经过多种方法的试算，并考虑到与所选样本距离的一致性，决定选用离差平方和法(Ward’s minimum-variance method)定义类与类之间的距离，其基本思想是比较不同类之间的离差平方和，将每一步离差平方和增加最小的两类合为一类，以满足“类内差异小，类间差异大”的原则。

最后，根据上述聚类方法对所有样本进行系统聚类分析，得到聚类结果树状图如图1所示。

图1 样本系统聚类分析结果树状图

上图中当以距离11划分时，可分为三类：第一类包含的样本为2，4，6，10，11，12，13，14，15；第二类包含的样本为1，5；第三类包含的样本为3，7，8，9。

第二类中样本1和5之间的距离较小，说明两段围岩工程性质非常接近。对比两者的各项指标，可以发现两者只有渗水情况有一定的差异，其他三项指标非常接近。它们的突出特点是岩石的单轴抗压强度较高，岩体完整性较好，岩体总体质量较好，利于施工。所以，可将Rc作为该类的主导因素，但是需要考虑地应力的影响，如果在高地应力区则需要考虑岩爆的可能性。

第三类中样本的各项指标均较差，特别是渗水情况都达到了经常渗水的级别，可以将渗水情况定为该类的主导因素。进一步分析样本间差异，可见样本7和8节理分布情况最差，具有大量接近洞轴线走向分布的节理，对工程的影响较大，所以可将节理分布情况作为二者的次主导因素。针对7号和8号样本的工程措施建议中，在隧洞轮廓线成形方法及支护方式的选择等方面应当予以重点考虑。

第一类中的各个样本性质介于以上两类之间，各项指标有一定的离散性但并不突出，所以该类可不设主导因素。进一步观察分类结果，样本2，10和12渗水情况为干燥或湿润，说明三者在区域地下水并不发育，可将渗水情况作为样本2，10和12的次主导因素。

综上所述，第一类无主导因素，样本2，10和12的次主导因素为渗水情况；第二类主导因素为Rc；第三类主导因素为渗水情况，样本7和8的次主导因素为节理分布情况。

2.4 铁路隧道围岩分级方法优化

由以上分析可见，所有样本根据相似性被分为了三类，同时根据其主导因素和次主导因素的不同而进一步被细化。将分级结果与聚类结果相结合，就可以对铁路隧道围岩分级进行优化，据此思想对工程实例中各研究段落进行优化(见表3)。

表3 研究段落围岩分级优化结果

表3中围岩级别后第一个字母表示样本主导因素，A为Rc，B为Kv，C为渗水情况，D为节理分布情况，无主导因素为0；第二个字母表示样本次主导因素，字母意义与第一个字母相同。

依据上表中的优化结果可知，系统聚类方法的引入使得铁路隧道围岩分级更加合理和有针对性，使具有突出特性的岩段能够清晰的表现出它们的主要影响因素和次要影响因素，从而使后续设计更具有针对性，例如在设计中首先按照岩段所属级别进行初步设计，然后根据主导因素进行针对性设计，最后再参考次主导因素完善设计，这种优化成果的应用必然会对工程的整体性产生积极影响。

3 结论

系统聚类分作为一种简单易行的多元分析方法，将其应用于铁路隧道围岩分级分析中是合理的，依据聚类分析结果进行优化后，围岩的主导因素与次主导因素具体指出了影响工程的主要工程地质特性，为后续设计和施工提供了具有针对性的指导。

铁路隧道围岩分级方法的优化能够细化工程条件，该方法是对现行规范分级方法的优化和完善，也为今后隧道围岩分级合理发展提供了新的思路。

综合上述实例分析可见，系统聚类分析方法是一个动态的分类过程，随着样本数的增加会使分类更趋合理化，能够更加清晰的揭示出各路段的相互关系。该方法的工程实例较少，仍需在今后的实际工程中进行完善。

[1] 何发亮，王石春.铁路隧道围岩分级方法研究及发展[J].铁路工程学报，2005(增)：392-397

[2] 周翠英，张亮，黄显艺.基于改进BP网络算法的隧洞围岩分级[J].地球科学-中国地质大学学报，2005，30(4)：480-486

[3] 史秀志，周健.隧道围岩分级判别的未确知均值聚类模型[J].土木建筑与环境工程，2009，31(2)：62-67

[4] 张庆飞，巫锡勇.灰色聚类法在围岩分级中的应用[J].西部探矿工程，2005(5)：112-113

[5] 秦松柏，欧阳正平，程天舜.分层聚类分析在水文地球化学分类中的应用[J].地下水，2008，30(1)：21-24

[6] 李志勇，邹静蓉，谢强.红层路堑边坡工程地质及系统聚类分析研究[J].工程勘察，2002(2)：5-7

[7] 彭铁华，童光明.聚类分析在红砂岩边坡工程地质分类中的应用[J].铁路与汽运，2003(95)：49-51

[8] 张立杰，刘琦，张焕智.聚类分析方法及其在水文地质分析中的应用[J].长春科技大学学报，1999，29(4)：349-354

[9] 周志军，潘三军，杨培慧.SPSS模糊聚类分析法在水质监测断面聚类分析中的应用[J].仪器仪表与分析监测，2007(4)：32-35

OptimizationStudyoftheStageDivisionofRailwayTunnelSurroundingRockBasedontheHierarchicalClusteringMethodology

YAN Ming

2014-07-01

闫 明(1987—)，男，2013年毕业于吉林大学桥梁与隧道工程专业，硕士，助理工程师。

1672-7479(2014)05-0071-03

U451+.2

： A