Matlab在土工试验数据分析中的应用

焦艳龙

(铁道第三勘察设计院集团有限公司，天津 300251)

Matlab在土工试验数据分析中的应用

焦艳龙

(铁道第三勘察设计院集团有限公司，天津 300251)

土的灵敏度是评价土体结构性的重要参数，其值大小受多种因素影响。以天津某地铁项目大量试验数据为基础，主要考虑孔隙比和塑性指数两种影响因素，运用Matlab语言对试验数据进行统计分析，得出了天津地区土体灵敏度与孔隙比、塑性指数两种影响因素的函数关系，并对试验数据中出现的异常值进行分析。

土体灵敏度 无侧限抗压强度 方差分析 回归分析

土体灵敏度是黏性原状土无侧限抗压强度与原状土结构完全破坏的重塑土无侧限抗压强度的比值，反映了黏性土结构性的强弱。土体受扰动后，随着静置时间的增长，土体强度又逐渐增加，但一般需要较长的时间，而且不能恢复到原来的强度。因此，在工程设计和评价时，应该充分考虑施工的扰动程度以及扰动引起的土体强度降低。

考虑到孔隙比、塑性指数两种因素对灵敏度的影响，利用Matlab软件对天津某地铁项目的大量试验数据进行统计，通过方差分析确定各个因素与灵敏度是否显著相关，然后通过回归分析拟合出函数关系式。

1 试验数据整理与读取

1.1 试验数据整理

土工试验数据汇总后，最终生成excel格式的成果报告，从中筛选出具有灵敏度指标的样品。为了便于统计，仅复制报告号、样品号、取样深度、孔隙比、塑性指数、灵敏度等列的数据，存放于新建的data.xls(如D盘根目录下)文件sheet1工作表中。孔隙比取0.45～1.3，间隔0.05；塑性指数取6.5～22.5，间隔0.5。孔隙比与塑性指数及相应的灵敏度试验数据分别存放于data.xls文件sheet2、sheet3工作表。

1.2 试验数据读取

Matlab是美国MathWorks公司上世纪80年代中期的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，自Matlab6.5(含)以后均支持读取excel文件，函数名为xlsread，使用方法为num=xlsread(filename， sheet， range)，参数分别代表文件名、工作表名、单元格范围。比如num=xlsread(‘d:\data.xls’，’data’)，表示将D盘下data.xls文件中data数据返回给num 。

2 灵敏度与各影响因素的关系分析

2.1 地铁沿线地质条件分析

天津地铁沿线为沉积平原，以陆相沉积为主，受海水涨退的影响，形成海陆交互沉积层。利用scatter函数绘制取样深度、塑性指数及灵敏度的散点分布见图1。

m=xlsread(‘d:\data.xls’，’sheet1’);

dep=m(:，3); %取样深度(m)

ip=m(:，5); %塑性指数

st=m(:，6); %灵敏度

scatter(dep，ip，100，st); %绘制散点分布图

同理，可绘制取样深度、孔隙比及灵敏度的散点分布图。

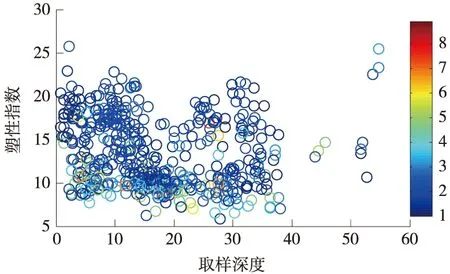
图1 取样深度、塑性指数及灵敏度散点分布

0～15 m，以黏土、粉质黏土、淤泥质土为主，局部有粉土，土的触变性和灵敏度较高，工程性质较差；15～25 m，以粉质黏土、粉土为主；25～35 m，以黏土、粉质黏土为主，局部夹杂有粉砂；40 m以下由黏土、粉质黏土组成，由于取样点较少，代表性有一定局限。

土体灵敏度集中在1～4之间，部分试样的灵敏度达到了6以上，主要为中、低灵敏土。

2.2 灵敏度与孔隙比的关系分析

利用单因素方差分析研究孔隙比的不同水平是否对灵敏度产生了显著影响。在Matlab中输入以下命令：

m=xlsread(‘d:\data.xls’，’sheet2’);

[p，table，stats]=anova1(m);

得出概率值p=0.001 4<0.01，表明孔隙比的影响高度显著，极具统计意义。图2是anova1函数生成的试验数据箱形图，灵敏度异常值用“+”标注。

图2 孔隙比与灵敏度试验数据

将异常值剔除，并对各级孔隙比下的灵敏度求均值，得到两者之间的对应数据，见表1。

表1 孔隙比与灵敏度的试验数据

利用plot函数绘制孔隙比与灵敏度关系曲线图，见图3。由图3可知，当孔隙比小于1时，灵敏度随着孔隙比的增大而减小；当孔隙比大于1时，灵敏度随着孔隙比的增大而增大，形成一条抛物线。

利用regress函数拟合出两者之间的回归方程。程序代码如下：

m=xlsread(‘d:\data1.xls’，’sheet1’);%表1中的数据存放于data1.xls文件sheet1工作表，首列存放孔隙比，次列存放灵敏度。

e=m(:，1);st=m(:，2);

x=e.*e;

y=[ones(length(e)，1)，e，x];

[b，bint，r，rint，stats]=regress(st，y);

孔隙比与灵敏度的回归方程为

其相关系数为0.825，概率值p<0.01，回归模型成立，结果显著。

图3 孔隙比与灵敏度关系曲线

2.3 灵敏度与塑性指数的关系分析

对塑性指数与灵敏度试验数据进行单因素方差分析，得出概率值p=5.74e-09<0.01，表明塑性指数的影响高度显著，极具统计意义。图4是anova1函数生成的试验数据箱形图。

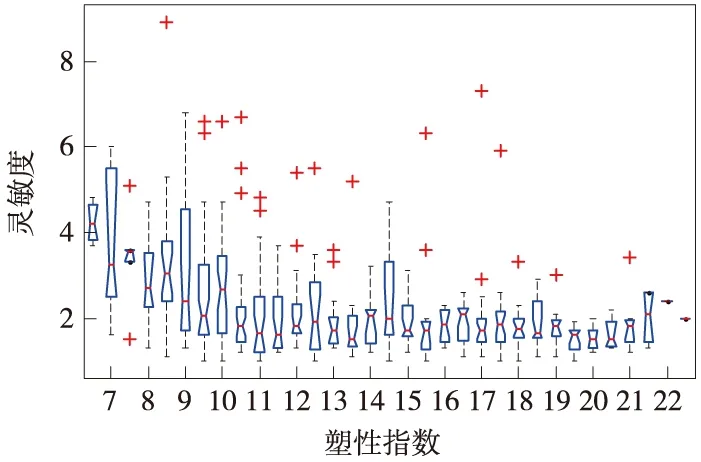
图4 塑性指数与灵敏度试验数据

剔除异常值后求均值，得到塑性指数与灵敏度的试验数据，见表2。

利用plot函数绘制塑性指数与灵敏度关系曲线图，见图5。由图5可知，当塑性指数小于17时，灵敏度随塑性指数的增大而减小；当塑性指数大于17时，灵敏度随塑性指数的增大而增大，形成一条抛物线。

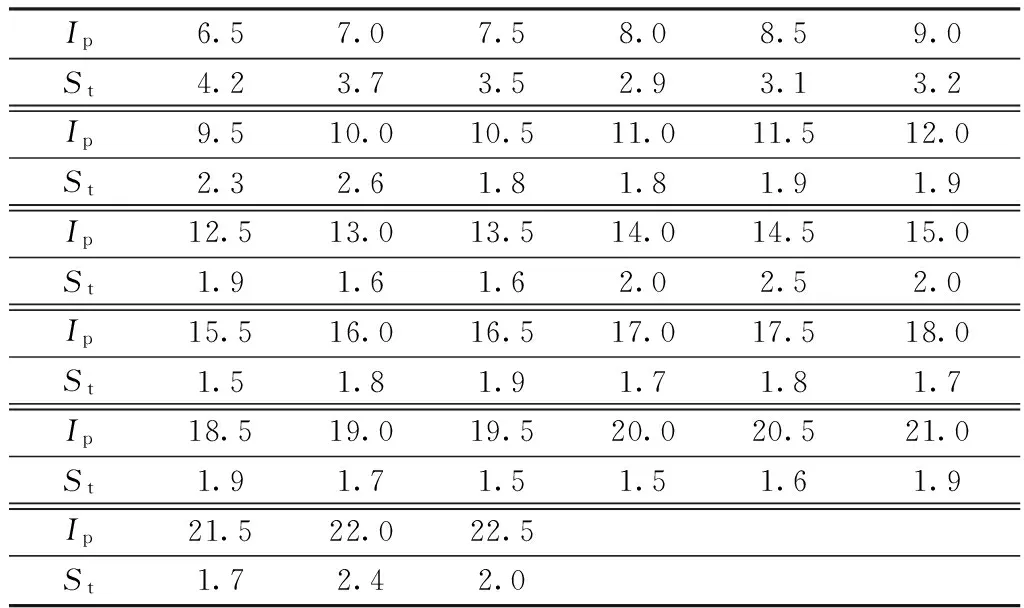
表2 塑性指数与灵敏度的试验数据

利用regress函数求得回归方程的系数，塑性指数与灵敏度的回归方程为

其相关系数为0.807，概率值p<0.01，回归模型成立，结果显著。

图5 塑性指数与灵敏度关系曲线

3 灵敏度异常值分析

箱形图中标注出的灵敏度异常值大部分在4.0以上，分析这些试样的物理指标可知，试样属于稍湿或湿的密实粉土，或者掺杂粉土的粉质黏土，应力—应变曲线具有极大的相似性，见图6。

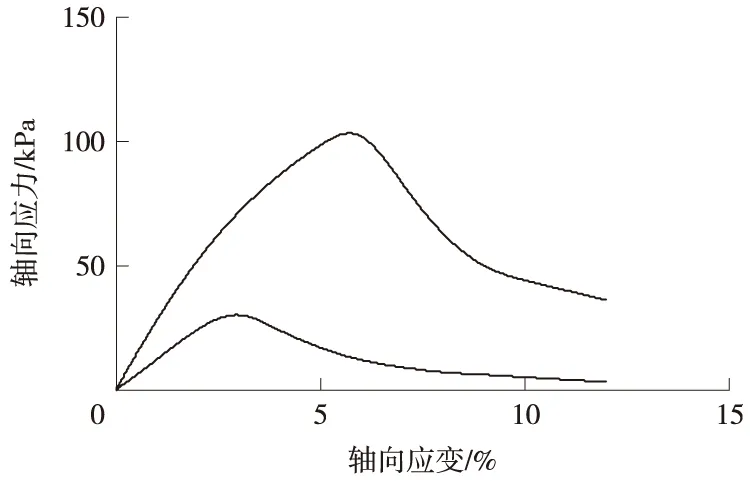
图6 灵敏度异常值应力-应变曲线

由图6可知，无论是原状土还是重塑土，剪切过程中均出现明显的峰值；剪切峰值出现在5%轴向应变附近；原状土的剪切峰值一般大于100 kPa。

塑性指数接近于10的粉土或者粉质黏土，粉粒间往往被黏粒充填，细小颗粒表面形成黏性水膜，土粒与土中水相互作用明显，这时土具有一定的粘滞性和结构性，力学强度高。土样剪切和重塑过程中，往往不可避免地造成水份蒸发流失，重塑试件变得松散，土颗粒间的联结作用降低，加之试件四周无外加约束应力，重塑试件的抗剪强度主要由颗粒间的摩擦力组成。

4 结论

考虑了两种影响土体灵敏度的因素，确定了天津地区土体灵敏度和孔隙比、塑性指数的关系。

当孔隙比小于1时，灵敏度随着孔隙比的增大而减小；当孔隙比大于1时，灵敏度随着孔隙比的增大而增大，形成一条抛物线；当塑性指数小于17时，灵敏度随塑性指数的增大而减小；当塑性指数大于17时，灵敏度随塑性指数的增大而增大，形成一条抛物线。

建立土体灵敏度和孔隙比、塑性指数回归方程

St=2.445 8e2-5.190 4e+4.621 1

St=0.019 5Ip2-0.664 6Ip+7.241 3

其相关系数分别为0.825和0.807，回归方程具有较好的相关性。

受土的天然特性以及人为因素的影响，部分土的灵敏度实测值偏大，试验过程中应注意区分，必要时进行补做。土体灵敏度的定义针对的是黏性土，考虑到非黏性土扰动失水或者液化后，结构强度大大降低，而且短期内很难恢复，在工程设计和评价时，更应考虑灵敏度异常值的影响。

[1] TB10102—2010铁路工程土工试验规程[S]

[2] TB10012—2007铁路工程地质勘察规范[S]

[3] 崔可锐.岩土工程师实用手册[M].北京：化学工业出版社，2007

[4] 高秀梅，等.新建天津某大功率机车综合检修基地岩土工程勘察分析及评价[J].铁道勘察，2011(5)

[5] 张霞云.浅谈蓟港铁路主要工程地质问题及评价[J].铁道勘察，2012(3)

[6] 曹晓娟.静止侧压力系数测试方法的探讨[J].铁道勘察，2014(1)

[7] 樊向阳，等.上海地区土体灵敏度的研究[J].岩土工程技术，2004(3)

[8] 徐宏伟，等.抗剪强度指标的主要影响因素[J].赤峰学院学报：自然科学版，2009(10)

[9] 吴泊人.浅议粉土的工程特性[J].安徽建筑，2002(1)

[10]杨加义.基于Matlab在Word中插入函数图形[J].电子设计工程，2011(4)

DataanalysisofgeotechnicalexperimentusingMatlab

JIAO Yan-long

2014-08-18

焦艳龙(1981—)，2005年毕业于兰州交通大学测控技术与仪器专业，工程师。

1672-7479(2014)05-0042-03

TU411.6

： B