基于互信息准则的图像平滑和分割

温铁祥潘正洋辜 嘉(中国科学院深圳先进技术研究院深圳58055)

2(中国科学院大学北京100049)

3(中国科技大学合肥230000)

基于互信息准则的图像平滑和分割

温铁祥1,2潘正洋1,3辜 嘉1
1(中国科学院深圳先进技术研究院深圳518055)

2(中国科学院大学北京100049)

3(中国科技大学合肥230000)

在计算机视觉领域，尺度空间扮演着一个很重要的角色。多尺度图像分析的基础是自动尺度选择，但它的性能非常主观和依赖于经验。基于互信息的度量准则，文章提出了一种自动选取最优尺度的模型。首先，研究专注于基于形态学算子的多尺度图像平滑去噪方法，这种技术不需要噪声方差的先验知识，可以有效地消除照度的变化。其次，通过递归修剪Huffman编码树，设计了一个基于聚类的无监督图像分割算法。一个特定的聚类数从信息理论的角度来看，提出的聚类算法可以保留最大的信息量。最后，用一系列的实验对算法的性能进行了验证，并从数学上进行了详细的证明和分析，实验结果表明本文提出的算法能获得最优尺度的图像平滑和分割性能。

尺度选择；高帽变换；互信息；形态学

1 引 言

尺度空间在许多领域的数学建模过程中是一个很重要的概念，但尺度的选择非常复杂。在各研究领域，如：化学、物理、生态系统等，宏观的连续行为产生于微观粒子(分子、细胞、人群中的个体)之间的相互作用以及它们与周围环境的之间的相互作用。在许多情况下，可通过使用各种宏观模型的推导(仿真、优化、分岔分析)对一个宏观模型(流体流动的Navier-Stokes方程或反应扩散方程)进行定量的描述[1–3]。然而，对于许多复杂的系统，尽管演化是在宏观尺度变换下观察的，但是准确的模型只能在给出更精细尺度和微观模型上进行描述，如：格子玻尔兹曼、活性粒子动力学理论、分子动力学、元胞自动机等[4–6]。最近，在物理化学建模方面，宏观和微观的联系已取得了初步的成效[7–9]。

尺度空间理论的应用非常广泛，而尺度空间中尺度之间的联系却是复杂的。本研究只关注在图像处理任务方面的最优尺度选择。尺度分析是许多图像处理任务方面最有用的框架之一[10–12]。分层多尺度表达的基本思想是分析有关尺度变换[13,14]，而它通常被定义为被过滤后的图像集合。

在一些经典文献中，多尺度表示可以区分为三种类型：第一类是小波变换[15]，它在图像处理领域被广泛应用，如：图像去噪[16]、图像和视频压缩[17,18]及多模态图像配准[19]。通过采用可变大小的窗口技术，小波变换可以把一个信号分解成多尺度表示；第二类是基于偏微分方程的扩散过程[20]，它源于传统的各向同性热流动方程，并已广泛使用在图像滤波[21–24]，分割[25–27]和图像修复[28–30]；第三类是基于数学形态学[31–33]。大多数形态过滤器产生非线性尺度，与线性尺度分析相比，它在绝大多数图像处理任务方面已经表现出了卓越的性能。如：一幅图像的特征(边缘、角落等)可以很好的用非线性算子保留起来。

尺度是多尺度分析应用中的关键参数，它的性能好坏决定了多尺度算法的成功与否。最近，一些现有的选择合适尺度去除图像噪声的技术已经被提出，这些技术通过最优控制理论[34,35]、奇异摄动方法[36]、最小化相关信号和噪声[37]、统计模型[38,39]和马氏随机场模型[40]获得最优的尺度。然而，这些方法需要预先知道噪声方差，且它的评估运算非常耗时，有时也不切实际。为了提高尺度选择的鲁棒性，本文基于信息理论模型[41]，提出了一种新的尺度选择的算法，该算法是基于最大化互信息来表示形态学多尺度。

此外，本文提出的尺度选择模型可以用于无监督图像分割，其中的聚类数(Number of Cluster, NC)的确定被认为是最优尺度选择。测量的标准来源于互信息的计算。互信息标准已经在基于二进制空间的图像分割方法[42]、模拟退火法[43]和模糊C-均值法(FCM)[44,45]中被采用。不同于那些方法，本文所提出的算法可以保持与原始图像和分割后的图像之间的最大信息量，并且模型解的凸性也可以通过采用哈夫曼编码策略加以保证，并在数学上对算法良好的性能进行了证明。

本文第2部分详细描述了建立在互信息最大化目标函数的基础上的尺度选择模型和它在图像去噪和分割方面的应用。第3部分介绍实验结果，第4部分对结果进行讨论。

2 互信息准则模型

2.1 模型的描述

在信息理论中，互信息被定义为一种统计学上对两个随机变量X和Y的相关性测量。将图像u(x)看作一个随机变量，则u(x)的概率密度可表示为pu(i)，并且通常可从图像直方图中可以估计出来。那么，给定两幅图像u(x)和v(x)，它们间的互信息I(u,v)可以写为：

其中，H(u)表示香农熵，表示一个随机变量的平均信息或不确定性，并且只有在同等概率的情况下，H(u)表示的信息量达到最大。H(u,v)表示的是u(x)和v(x)的联合熵，表达了这两个变量之间的匹配性。puv(i,j)是衡量u(x)和v(x)之间的相似性的联合概率。联合概率可以定义为：

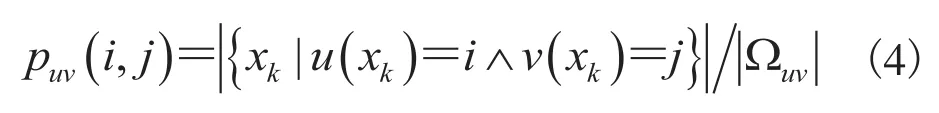
在随机变量u(x)和v(x)正确匹配的情况下，互信息量达到最大化。为了表示原始图像u(x)和用多度算法处理后图像之间的关系，我们定义一个基于信息理论的能量函数Jt如下：

其中，Pt是尺度为t的一个操作算子，如：用于图像去噪的形态学开操作算子和用于图像分割的聚集操作算子。

通过寻找多尺度 t，最大化互信息函数：

原始图像和处理后的图像之间的互信息可表示为：

原始图像和处理后的残余图像之间的互信息计算可表示为：

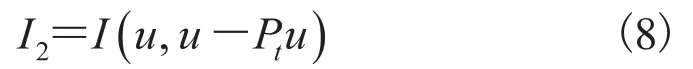
随着尺度变量t的增长，可以看出来公式(7和(8)之间的互信息量的增长方向是相反的：一个在增长的同时另一个在下降。为了便于比较公式(7)和(8)，我们归一化并重写为：

在本文下面的章节中，分别用上面化一归的方程作为图像去噪和分割上问题上尺度选择的标准。

2.2 基于互信息最大化的图像去噪

2.2.1 去噪算法的描述

这一节将介绍基于多尺度表示的形态学开操作算子的图像去噪算法，用具体的开操作算子Ot取代公式(9)和(10)中的尺度算子。开操作是膨胀和腐蚀操作的结合，是数学形态学中的基础操作。其中，结构元素形状和尺寸大小的选择非常基础和重要。然而，对于一幅具体图像的处理任务，结构元素的选择往往依靠主观和经验。为了自动地选择结构元素，我们从多尺度的观点出发，用尺度t参数化结构元素的大小并且重新定义基础的形态算子。这样，对于一个具体的图像处理任务，选择结构元素的尺寸问题便成了选择合适大小或者最优尺度的问题。

膨胀算子D计算的是在给定邻域的灰度最大值，结构元素用尺度t进行参数化，膨胀算子可表述为：

当图像被膨胀处理后，那些比结构元素更小的图像细节(如：噪声等)将从图像中消除。当尺度t从0开始增大时，能获得一系列过滤后的图像。

相反地，腐蚀因子E计算邻域附近的灰度最小值，定义为：

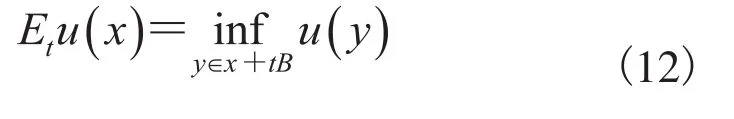
然后开操作算上O可以被定义为在腐蚀运算后再进行膨胀运算：

用泰勒展式展开公式(13)，可得：

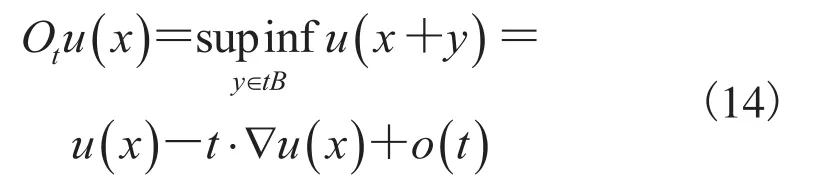
其中，o(t)是关于尺度t的高阶无穷小量，▽u(x)是原始图像u(x)的梯度。因此，随尺度t的减小，开操作运算的极限为：

同时，随尺度t的增大，开操作运算的极限为：

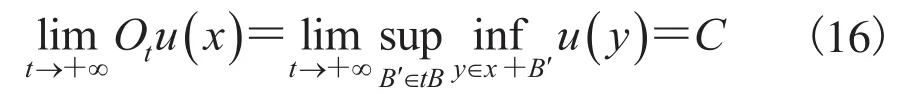
其中，C是常数。公式(16)表示：如果选定的尺度足够大，通过开操作运算得到的滤波后图像是一个常量。

原始图像与开操作运算的残差恰好为高帽变换：

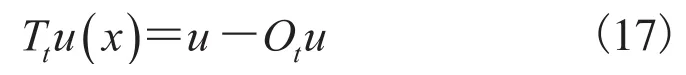
开操作算子可以有效地抑制图像中的细节信息，因此，当开操作图像从原始图像减去后，就可以获得所需的细节[46]。高帽变换的其中一个潜在应用是估量不均匀的背景光照。然而，如果尺度过小，高帽变化会对不均匀光照估计不足。反之，高帽变化会对不均匀光照估计过度。也即，如果选择的尺度太小的话，从高帽变换得到的结果会对噪声很敏感。另一方面，如果选择的尺度太大的话，高帽变换对原始的图像起不了作用，因为对大尺度时开操作的结果是一个常量图像。利用公式(16)和(17)，以上结论可用数学公式描述为：

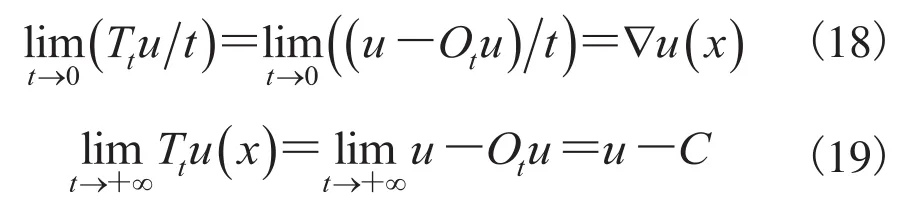
为了给基于高帽变换的图像去噪选择合适的尺度，利用互信息公式(9)和(10)作为定量标准，给出如下的尺度选择算法(i-De)。

Algorithm:i-De

Parameter:

Denote T as the number of iteration, at the initial scale t＝1.

Do fort＝2, …, T

1.Compute top-hat transformation as in (17);

2.Calculate mutual information I1and I2as follows: as a small threshold parameter.

Calculate

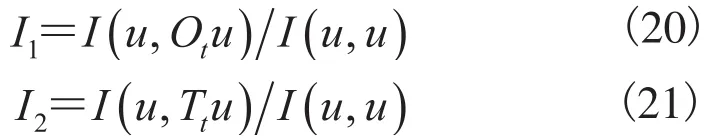
2.2.2 i-De算法的分析

对于i-De算法的可行性，将对其中公式的单调性给出相关证明。下面首先介绍与开运算相关的定理。

定理1：令为一函数集，并且它在对比度变化的情况下保持稳定，另外O是一个具有sup-inf运算形式的算子，定义为：那么，sup-inf算子是单调的并且在对比不变的。

根据定理1给出的开操作算子的单调性，下面介绍两个描述公式(20)和(21)性质的命题。

命题1：令O是一个开操作算子，T是一个高帽变换，I(u,v)是两个随机变量u(x)和v(x)的互信息。那么，公式(20)定义的互信息是单调递减的，公式(21)定义的互信息是单调递增的。

证明：公式(15)和(16)表明开操作后的图像在尺度为0时是原始图像，在尺度为无穷大时趋于常量图像。结合定理1中的单调性，可以得出：随着尺度从零增加到无穷大，开操作后图像Otu(x)将从原始图像单调下降为常量图像。同时，因为最大化互信息只有当图像与自身进行互信息计算时才能获得，即。所以，可以得出结论：公式(20)的互信息是单调减少的。公式(21)的互信息是单调增加的。

在实验结果中，观察到公式(20)的互信息为单调减少，这和命题1的结论相吻合。然而，公式(21)的互信息为微小振荡地缓慢增加，但不是单调的。这一现象是由于公式(20)的计算对噪声不敏感。因为开操作图像可以看作是原始图像的一个平滑去噪过程。相反地，高帽变换图像是原始图像的开操作图像的残留图像。也即，高帽变换图像在小尺度时对于噪声敏感，正如公式(18)所示。这样的振荡是由噪声的存在所造成。但是公式(21)的互信息的趋势是增加的。

命题 2：公式(20)和(21)定义的互信息将会在某个尺度处相交。

证明：通过将公式(15)和(16)替换成(20)，我们可以得出结论：公式(20)的互信息从最大的互信息(即1)减少到最小的互信息(即0)。相似地，通过将公式(18)和(19)替换成(21)，我们可以得出结论：公式(21)从0增加到1。因此，公式(20)和(21)会在某个尺度处相交。

根据命题2，随着尺度t的增加，曲线(20)和(21)有一个相交点，并且这个交点是一个拐点，因为这两个互信息在此开始收敛。然而，正如在我们实验结果中表明的那样，该点的尺度不是最优的。i-De算法给出了最优答案。

尺度模型不仅解决了形态学中去噪的问题，而且解决了无监督聚类问题。下面我们给出另外一种基于尺度模型的无监督聚类算法，用于选择合适的聚类数目。

2.3 基于互信息最大化的图像分割

2.3.1 图像分割算法的描述

绝大多数无监督分割算法需要一些关于选择NC方面的先验知识。如，我们事先知道脑图像磁共振成像(MRI)可分为脑脊液、脑白质、灰质和背景。然而，没有特定的专业领域知识，我们通常很难甚至不可能知道真正的聚类数目。

本文在这一节中给出了一种在无监督图像分割中解决选择合适或者最优NC问题的算法，其中水平集函数通常用来描述对比度不变的属性[33]。一幅水平为t的图像通常写成，其中t∈R。这里，把一个特定的水平t当作图像分割的阀值。通过采用霍夫曼熵编码方法，采用预先设定的准则，算法可以把一幅图像递归细分成相似的区域。该算法和它的分析是基于章节2.1描述的信息理论函数以及霍夫曼熵编码方法。在每个阶段对图像直方图进行霍夫曼规则排序，保证了本文的互信息最大化的解不是局部的，而是全局最优的。用i-Se标记本文提出的基于互信息最大化的分割方法，它的伪代码描述如下：

Algorithm:i-Se

Parameter:

Denote T as the number of maximum intensity bin for an image u(x), S as the clustering operation.

Do fort＝T—1,…,2,1

1. Calculate probability density

2. Sort pu(i) in descending order;

3. Combine the lowest two ordered probabilities, and produce a weighted intensity as follows:

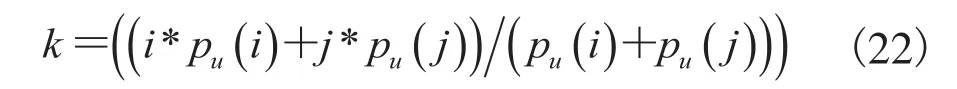
Now the probability of intensity k becomes:

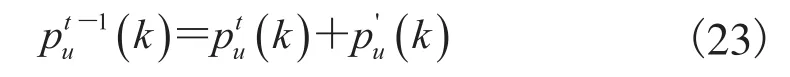
where

And the following diagram illustrates our clustering process based on Huffman coding strategy:

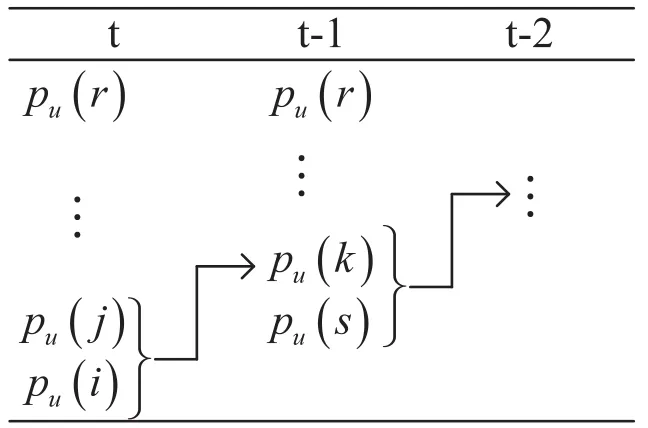
4. Calculate following mutual information:

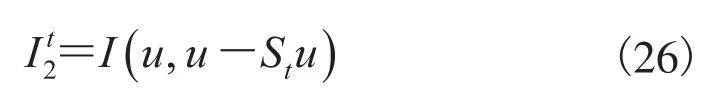
2.3.2 关于图像分割算法的分析

对于i-Se算法分析的主要目的是分析基于公式(25)的互信息函数单调性和光滑性，并进一步给出对于 i-Se 算法的解是凸的。从以下两个不等式开始(以下两个引理的证明见附录)。

引理1：令 p,q为概率密度函数，r＝p+q，那么有：—rlog(r)＜—(plog(p)+qlog(q))。

引理2：令 Stu(x)为图像u(x)在水平t上的分割图像，那么，联合熵H(u,Stu)在任何聚类t水平都保存不变。

由这两个引理，我们可以得出下面的命题。

命题3：令 Stu(x)为随机变量u(x)在聚类水平t上的分割图像，那么，随着尺度变量t的衰减，I(u,Stu)的互信息是单调减少的。

证明：为了证明上面的命题，我们只需要证明互信息I(u,Stu)比H(u,St—1u)大。由(1)式有：I(u,Stu)＝H(u)+H(Stu)—H(u,Stu)，并且I(u,St—1u)＝H(u)+H(St—1u)—H(u,St—1u)。根据香浓熵的定义和引理1有：H(Stu)＞H(u,St—1u)。根据已被证明的引理2有：I(u,Stu)＞I(u,St—1u)。

在i-Se算法中，哈夫曼编码树的构建对获得全局最小解起着非常重要的作用。否则，公式(25)互信息中的凸性得不到保证。这种非凸的解通常存在于经典的FCM算法，并且可以从电脑断层扫描(CT)的体模图像分类实验中观察到。也即，FCM的解决方法是局部最小值。为了寻找全局的解决方法，i-Se算法采用类似于哈夫曼冗余编码中的排序规则，通过合并两个最小的概率密度值来构建每一步最小的信息熵。同时，由命题3 可以得到：

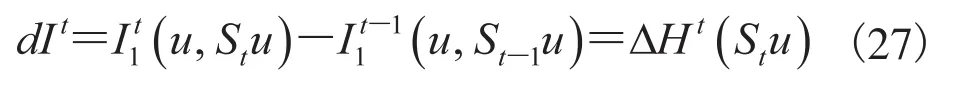
公式(27)表明：(25)式的互信息计算存在一些冗余项，因此，可以通过减少冗余项的计算来增加i-Se算法的计算速度。

Algorithm:i-Se(Simpli fied version)

Parameters:

Denote T as the number of maximum intensity bin for an image u(x),

S as the clustering operation.

Calculate entropy Ht(Stu)at scale t＝T.

Do fort＝T—1,…,2,1

1. Calculate probability density

2. Sortpu(i) in descending order;

3. Combine the lowest two ordered probabilities and produce a weighted intensity as in (22);

4. Calculate Shannon entropy as follows:

3 实验结果

3.1 去噪结果

在多尺度i-De去噪算法的实验中主要关注具有非均匀光照背景的图像，可以通过高帽变换有效地去除原始图像存在的非均匀光照[46]。变换后的图像被进一步分割，以验证i-De尺度选择算法。

图1(a)是一幅带有不均匀光照的原始米粒图像。运用阈值分割方法对原始图像进行分割，图1(d)中给出了分割结果。从中可以看到，图像底部的米粒不能理想地从非均匀背景中提取出来。Gonzalez等[46]曾指出只要结构元素足够大，对原始图像进行开运算后，非均匀光照能够被估算出来，但并没有给出具体的尺度选择方法。图1(b)诠释了尺度为6时的开操作图像，在这个尺度公式(20)和(21)的互信息相交，可以看到，在这个交点的尺度不是最优的，图1(b)中用圆圈标记出来的米粒的估计是不正确的。i-De尺度选择算法选择尺度为10，理想的结果见图1(c)和图1(f)。图2表明随着尺度t的增加，公式(20)和(21)的互信息将会相交。并且，它验证了在命题1中的I1和I2的预计：I1单调减少而 I2单调增加。然而，I1和I2不是凸函数，它的非凸性在图3中被表示出来了，其中它诠释了I1和 I2振荡的差异。

图1 米粒图像去噪Fig.1. Denoising for rice grains image

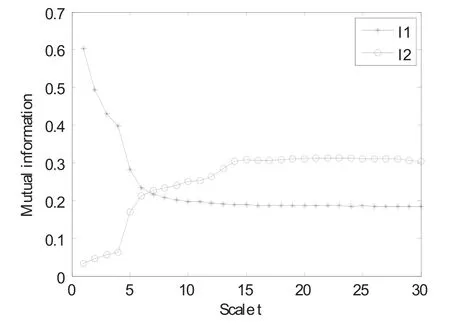
图2 各种不同尺度下米粒图像的(20)和(21)的互信息Fig.2. Mutual information of (20) and (21) for grains image at various scales

图3 图2中互信息的差Fig.3. Difference of mutual information for Fig. 2

图4为血管图像去噪结果。其中，(a)～(d)中的Ttu对应尺度分别为0、5、15、30；(e)～(h)为用水平集方法得到与(a)～(d)对应的分割结果；(i)～(k)表明了非均匀背景的估算：Otu相应的尺度t＝5，15，30。图4(a)是具有非均匀背景的X射线血管医学图像。图4(e)为用水平集方法[47]的分割结果。水平集在在血管左侧底部停止演化，表明水平集方法不能有效地对具有非均匀背景的血管图像进行分割。本文用高帽变换对血管图像中的非均匀背景进行消除。公式(20)和(21)的互信息和它们之间的差异分别见图5和图6，i-De尺度分割算法预测最优尺度为15，为了和其他尺度进行对比，选择具有代表性的尺度5和30。图4中(a)～(d)分别为尺度0，5，15，30处的高帽变换图像，(e)～(h)为用水平集法对滤波后的图像分割结果，(i)～(k)显示了对不均匀背景的估计。从这些图像可以看出，如果选择尺度过小，将会导致对非均匀背景的低估，正如图4(f)圆圈标记的那样，它将会导致血管边缘的泄露。另一方面，选择尺度过大，将导致对背景的过高估计。只有选择合适的尺度才会产生如4(g)那样理想的分割结果。

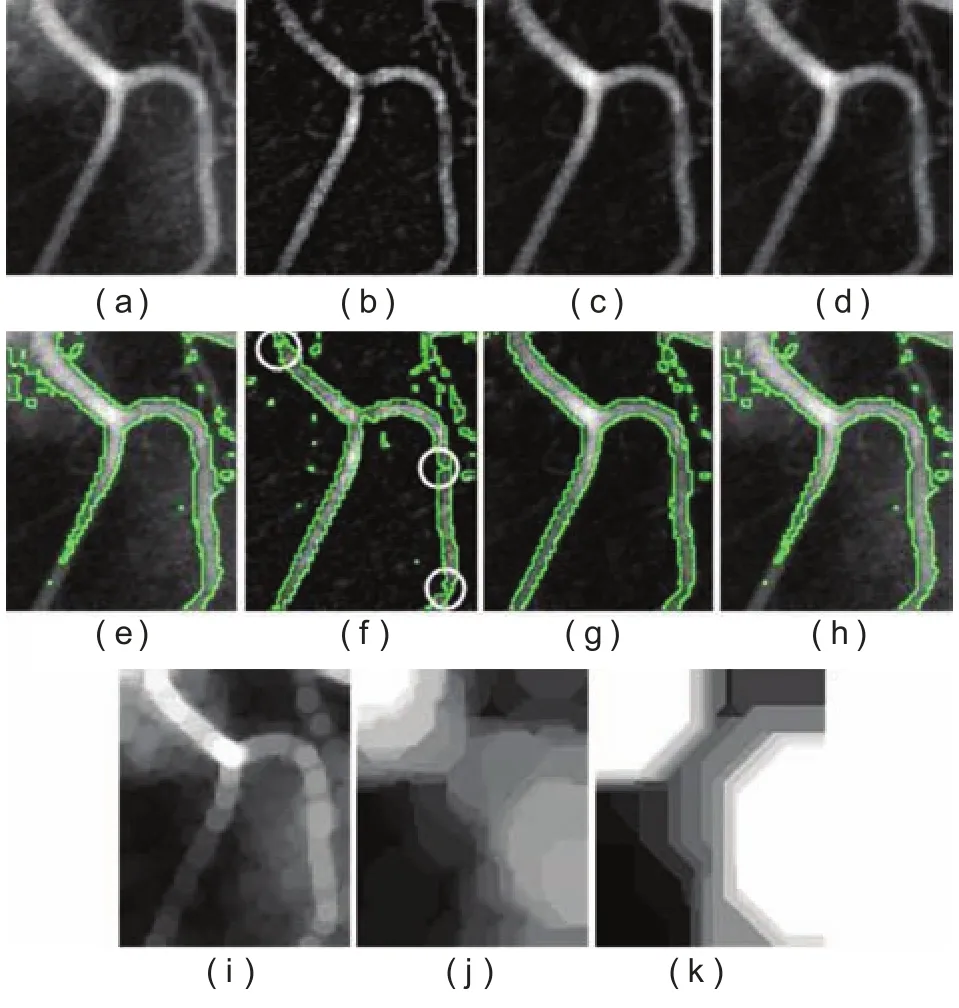
图4 血管图像去噪Fig.4. Denoising for vessel image

3.2 分割结果

测试i-Se算法的第一个实验是在一个Shepp-Logan体模图像上进行的，它被实验者广泛地用于验证它们任意二维CT重建算法的准确性。它具有六个已知的组织类型，其中的强度值分别为0，26，51，77，102和255。

图7和图8为用FCM和i-Se聚类方法得到的分割结果。在图9和10为互信息和NC之间的关系，其中公式(25)和(26)之间的互信息被绘制了出来。它验证了定理3中的结论：I1的互信息是单调增长并随着NC的增长汇聚于1。同时，I2单调减少并随着 NC后达到0。

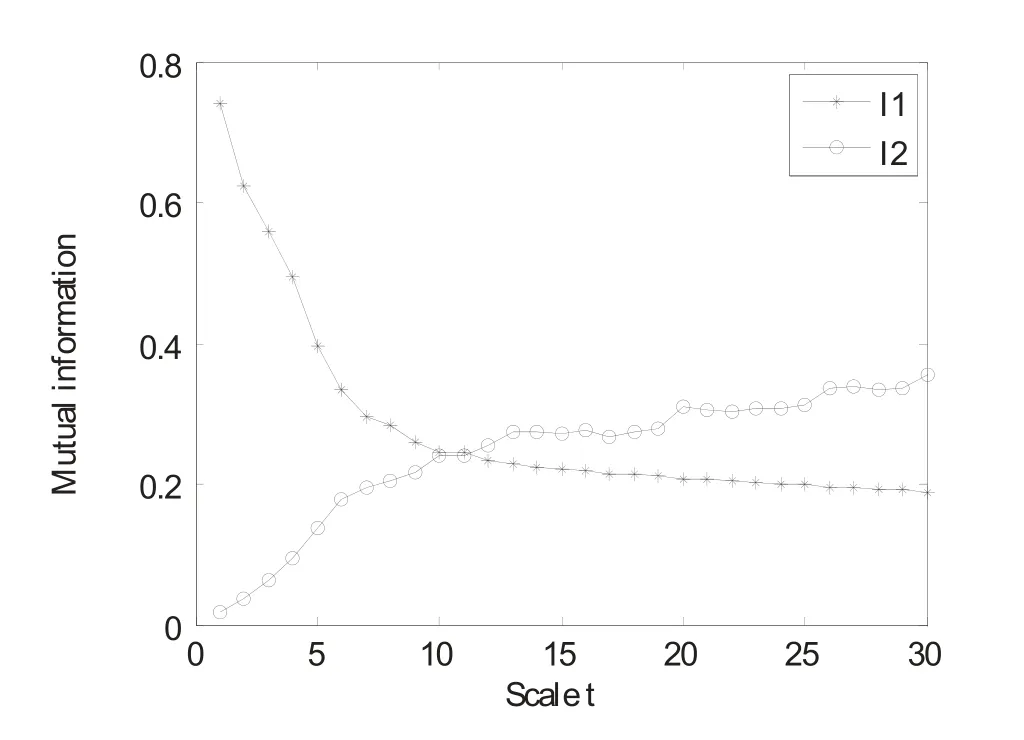
图5 各种不同尺度下血管图像的(20)和(21)互信息Fig.5. Mutual information of (20) and (21) for vessel image at various scales

图6 图5中互信息的差Fig.6. Difference of mutual information for Fig.5

图7 基于FCM算法的体模图像分割Fig.7. Segmentation of head phantom image using FCM method

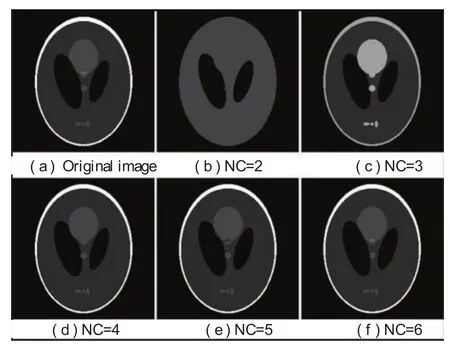
图8 基于i-S算法的体模图像分割Fig.8. Segmentation of phantom image using i-Se algorithm

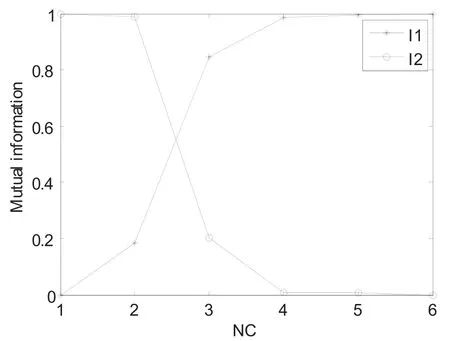
图9 针对体模图像FCM算法的互信息量Fig.9. Mutual information of FCM algorithm for head phantom image

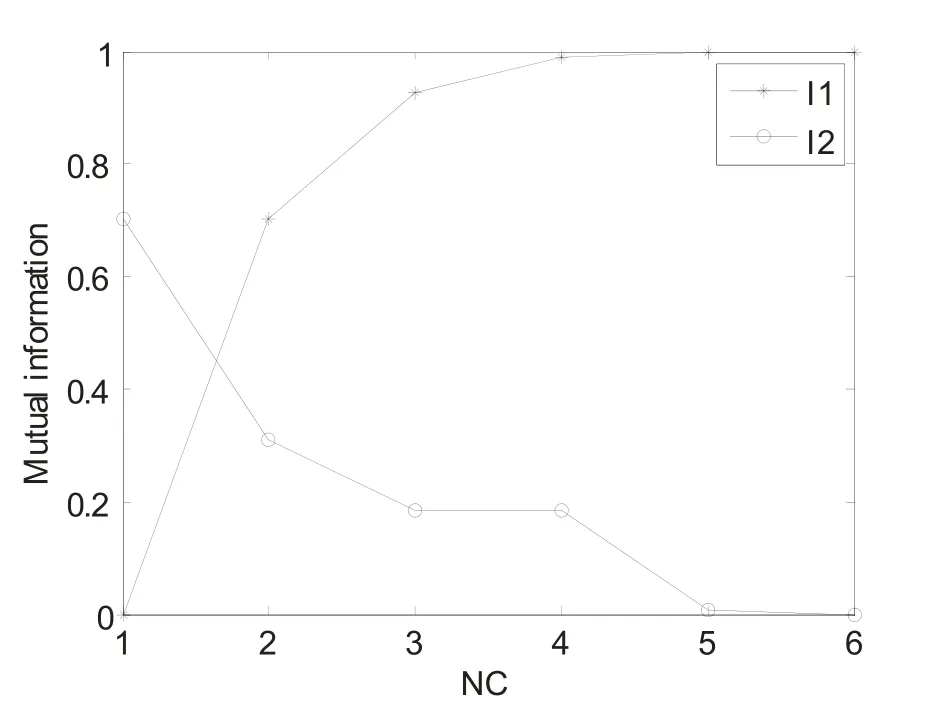
图10 针对体模图像i-Se算法的互信息量Fig.10. Mutual information of i-Se algorithm for head phantom image

图11 体模图像中FCM和i-Se算法在互信息方面的比较Fig.11. Comparison of mutual information for FCM and i-Se algorithm

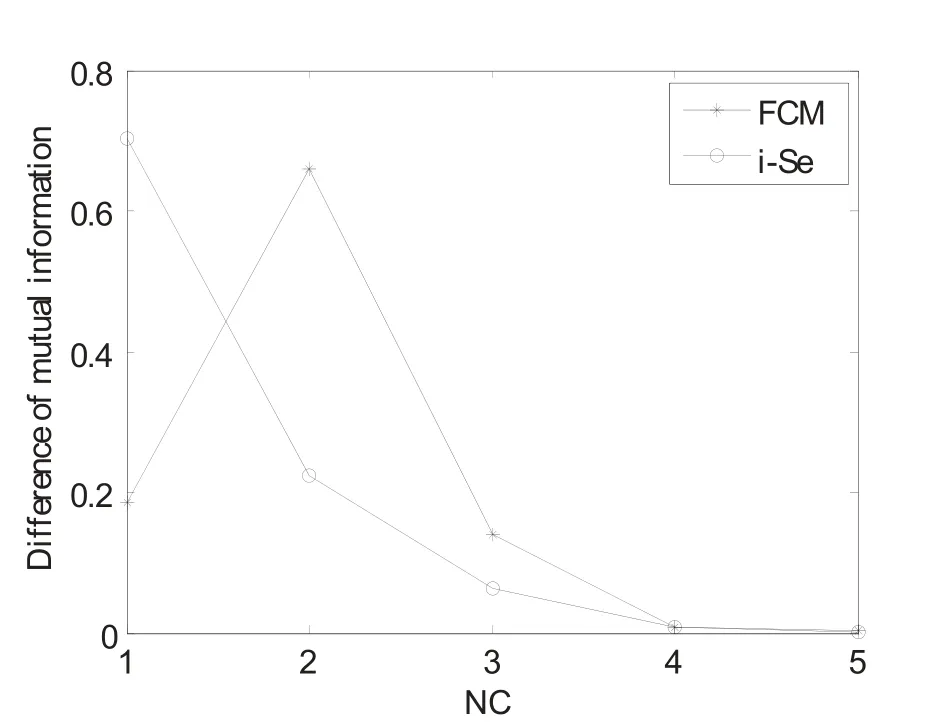
图12 体模图像中FCM和i-Se算法在互信息差方面的比较Fig.12. Comparison of the difference of mutual information for FCM andi-Sealgorithm

图11表明当NC是2或者3的时候i-Se算法的互信息量比FCM聚类算法的要多，这意味着i-Se算法的分割结果包含更多的图像细节，这可以通过比较图7(b)、(c)和图8(b)、(c)得到。同时，FCM方法是一种局部算法，而且它会根据聚类中心不同的初始化产生不同的分割结果。这种局部现象在图12中被很好地诠释了，其中这种局部算法不能保证互信息差的单调性。相反，图12表明了i-Se算法的互信息不同的曲线更平滑。更重要的是，它是单调减少的。

第二个测试i-Se算法的实验是在一幅真实的脑CT图像上进行的。它不是一幅合成图像并且我们没有预先知道准确的NC。图13为测试的CT图像及用FCM和i-Se算法得到的分割结果。互信息和NC之间的关系以及不同分别在图14和图15中表示了出来。如图14所示，随着NC的增加，i-Se和FCM算法的等式(25)的互信息都在增加。但是也可以观察出来，在NC相同的情况下，i-Se算法的互信息量比FCM算法的大。同时，与FCM的分割结果图像相比，更详细的细节信息被保存在i-Se分割图像中。随着NC的增加，这种优势更加明显。图15中，随着NC 的增加，FCM算法的互信息的差异的是减少振荡的，而随着NC的减少i-Se算法单调减少。

i-Se算法的第三个实验是在Lena图上进行的。实验结果见图16～18。把脑T图像和Lena图像之间的结果进行比较，我们的方法可以有效地保存分割图像的详细信息。在其它测试图像上进行了更多的实验，用来验证i-Se算法在揭示原始图像和分割图像内在关系上的有效性。

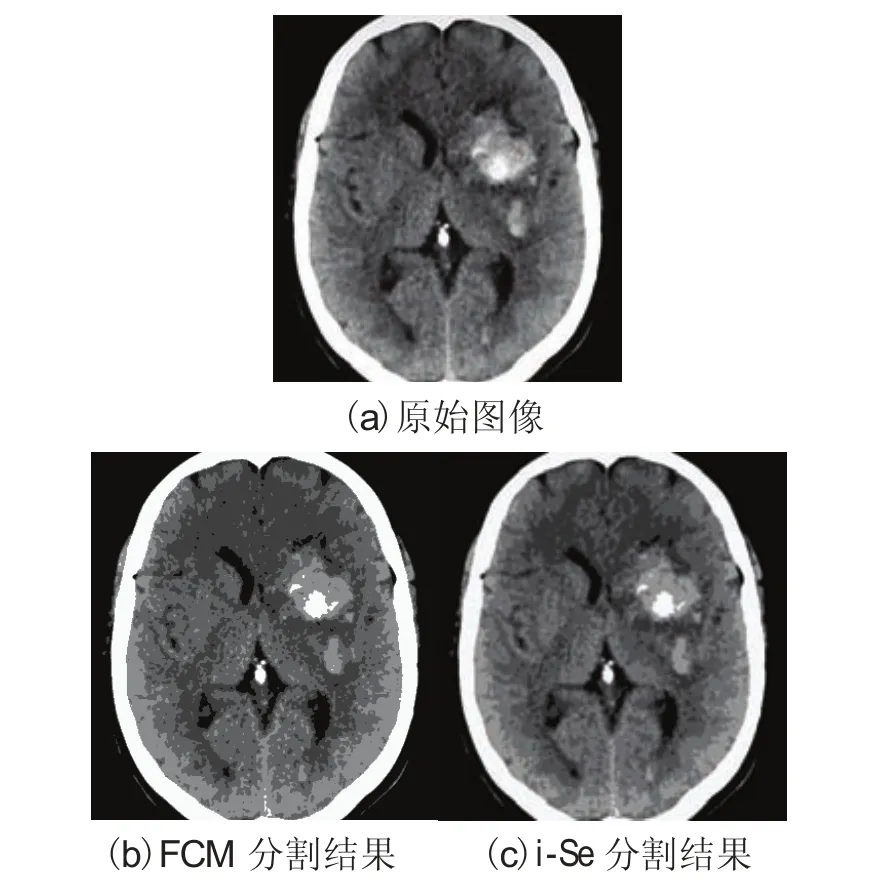
图13 CT图像分割Fig. 13. Segmentation for CT image

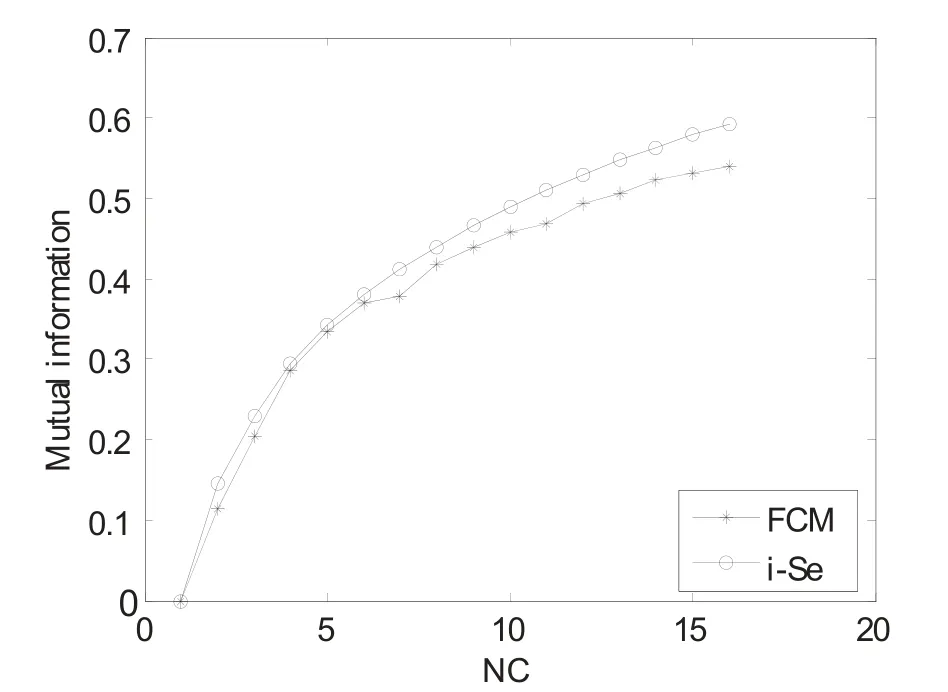
图14 CT图像中 FCM 和 i-Se 算法在互信息方面的比较Fig.14. Comparison of mutual information for CT image using FCM and i-Se algorithm

图15 CT图像中FCM和i-Se算法在互信息差方面的比较Fig.15. Comparison of the difference of mutual information for CT image using FCM and i-Sealgorithm

图16 Lena图像分割Fig.16. Segmentation for Lena image

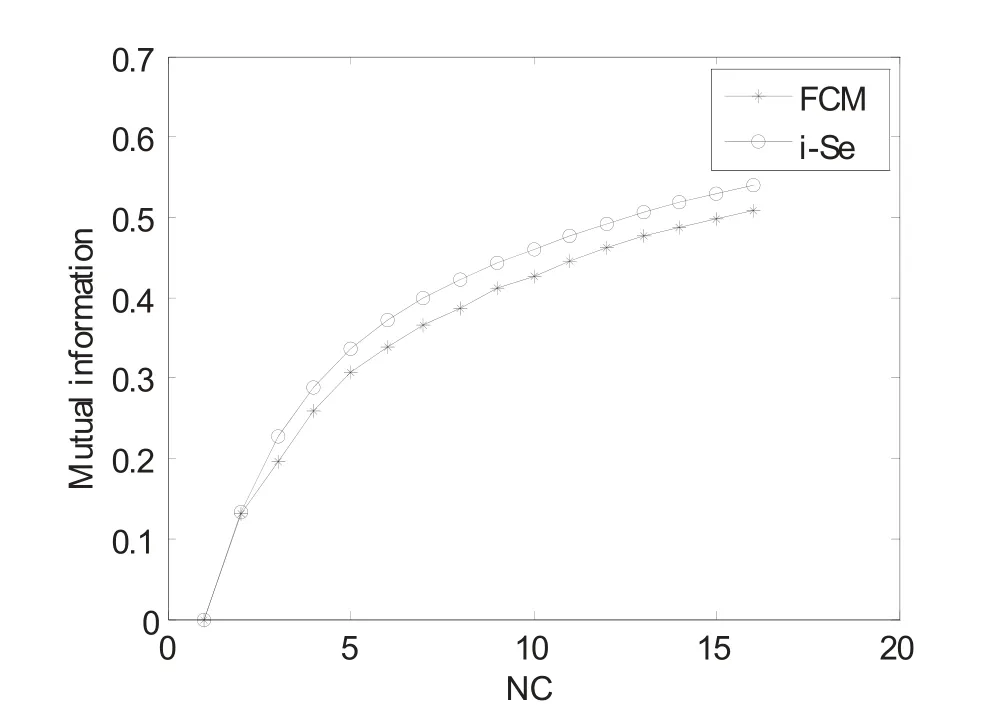
图17 Lena 图像中 FCM 和 i-Se 算法在互信息方面的比较Fig.17. Comparison of mutual information for Lena image using FCM and i-Se algorithm.

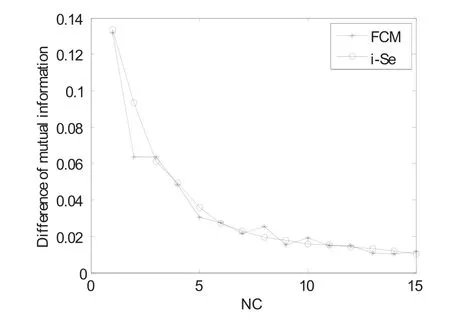
图18 Lena 图像中 FCM 和 i-Se 算法在互信息差方面的比较Fig.18. Comparison of the difference of mutual information for Lena image using FCM and i-Se algorithm

4 结果和讨论

在本文中，我们利用互信息作为在多尺度分析中最优尺度选择的相似性的衡量标准，应用到图像去噪和分割中。首先，我们表示了在多尺度分析中的图像处理算子并提出了互信息函数。对于形态学开操作算子，我们给出了一个i-De尺度选择算法，它的好处是使在多尺度表示的图像中让多尺度的选择自动化。对于聚类算子，我们给出了一种i-Se聚类算法，该算法通过把一个特定水平t当做图像分割的阀值。对于i-De和i-Se算法的可行性，我们对目标函数的单调性和平滑性做了详细的数学分析。

利用i-De算法，通过选择合适的尺度来消除不均匀背景。这种非均匀的光照在大多数相机或医疗图像中是一种常见的现象。i-Se算法输出了聚类分割的合适水平，在这样的尺度下，我们可以得到分割图像的最大量信息。

i-Se算法的一个缺点是模型中只考虑到灰色特征，其他的特征(如：像素之间的空间相关性、边界和纹理)没有被考虑到，需要一种更详细的局部模型来产生更可靠的结果。

许多其他的建模任务，如：化学、物理和生物建模，可以在尺度空间建模方面进行探索。然而，本研究的主要目标是为图像去噪和分割任务建立一种尺度选择标准。在未来，我们将会就关于我们的算法应用到其他的模型任务中做更多的工作，并且针对模型中现存的大多数限制进行研究解决。

附录

引理1：令p,q为概率密度函数，r＝p+q，那么有：—rlog(r)＜—(plog(p)+qlog(q))。

证明：因为p,q为概率函数，所以有和对于一个递增函数f(x)＝xa,a∈[0,1],x∈(0,∞)，可以得到：(p+q)p＞pp和(p+q)q＞pq。所以有：rr＝(p+q)p+q＝(p+q)p*(p+q)q＞pp*qq。两边取对数可得：rlog(r)＞plog(p)+qlog(q)。

引理2：令 Stu(x)为图像u(x)在水平t上的分割图像，那么，联合熵H(u,Stu)在任何聚类t水平都保存不变。

证明：对于自联合熵H(u,u)，我们有puu(i,j)i＝j≠0和puu(j,j)i≠j＝0。即自联合熵是一个对角矩阵。假设合并u(x)任意两个概率密度，如i和j，那么会产生一个如公式(22)的加权密度函数，以及Stu(x)的概率密度k变成了公式(23)。所以在对角矩阵H(u,u)上的联合直方图有如下的对角元素移动：puu(k,k)→puStu(k,k)，puu(i,i)→puStu(i,k)和puu(j,j)→puStu(j,k)。由于聚类的结果只在联合分布上移动元素，并不改变联合熵的整个值。即有H(u,u)＝H(u,Stu)。相似地，有H(u,u)＝H(u,St—1u)。因此有H(u,Stu)＝H(u,St—1u)，从而该引理得证。

[1] Spohn H. Large Scale Dynamics of Interacting Particles [M]. New York: Springer Berlin Heidelberg, 1991.

[2] Katsoulakis MA, Majda AJ, Vlachos DG. Coarsegrained stochastic processes and Monte Carlosimulations in lattice systems [J]. Journal of Computational Physics, 2003, 186: 250-278.

[3] Xiao L, Chen LX, Xiao JZ. A new algorithm for shortest path problem in large-scale graph [J]. Applied Mathematics Information Sciences, 2012, 6(3): 397-400.

[4] Pappalardo F, Palladini A, Pennisi M, et al. Mathematical and computational models in tumor immunology [J]. Mathematical Modelling of Natural Phenomena, 2012, 7(3): 186-203.

[5] Keunings R. Micro-macro methods for the multiscale simulation of viscoelastic flows using molecular methods of kinetic theory [J]. Rheology Reviews, 2004, 1: 67-98.

[6] Erban R, Othmer HG. From individual to collective behavior in bacterial chemotaxis [J]. SIAM Journal on Applied Mathematics, 2004, 65(2): 361-391.

[7] Alemani D, Pappalardo F, Pennisi M, et al. Combining cellular automata and lattice Boltzmann method to model multiscale avascular tumor growth coupled with nutrient diffusion and immune competition [J]. Journal of Immunological Methods, 2012, 376(1-2): 55-68.

[8] Bradley C, Bowery A, Britten R, et al. Open CMISS: a multi-physics & multi-scale computational infrastructure for the VPH/Physiome project [J]. Progress in Biophysics and Molecular Biology, 2011, 101(1): 32-47.

[9] Bellouquid A, Bianca C. Modelling aggregationfragmentation phenomena from kinetic to macroscopic scales [J]. Mathematical and Computer Modelling, 2010, 52(5-6): 802-813.

[10] Marr D. Vision [M]. Dallas: Freeman Publishers, 1982.

[11] Koenderink JJ. The structure of images [J]. Biological Cybernetics, 1984, 50(5): 363-370.

[12] Lindeberg T. Scale-space Theory in Computer Vision [M]. Norwell: Kluwer Academic Publishers, 1994.

[13] Witkin AP. Scale-space fi ltering [C] // Proceedings of the 8th International Joint Conference on Artif i cial Intelligence, 1983, 2: 1019-1022.

[14] Babaud J, Witkin AP, Baudin M, et al. Uniqueness of the Gaussian kernel for scale-space fi ltering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8: 26-33.

[15] Mallat S. A Wavelet Tour of Signal Processing [M]. Utah: Academic Press, 1988.

[16] Portilla J, Strela V, Wainwright MJ, et al. Image denoising using scale mixtures of Gaussians in the wavelet domain [J]. IEEE Transactions on Image Processing, 2003, 12(11): 1338-1351.

[17] Lewis AS, Knowles G. Image compression using the 2-D wavelet transform [J]. IEEE Transactions on Image Processing, 1992, 1(2): 244-250.

[18] Adami N, Signoroni A, Leonardi R. State-of-theart and trends in scalable video compression with wavelet-based approaches [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2007, 17(9): 1238-1255.

[19] Allen RL, Kamangar FA, Stokely EM. Laplacian and orthogonal wavelet pyramid decompositions in coarse-to-f i ne registration [J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3536-3541.

[20] Sapiro G. Geometric Partial Differential Equations and Image Analysis [M]. Cambridge: Cambridge University Press, 2001.

[21] Perona P, Malik J. Scale-space and edge-detection using anisotropic diffusion [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.

[22] Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms [C] // Proceedings of the 11th Annual International Conference of the Center for Nonlinear Studies on Experimental mathematics : Computational Issues in Nonlinear Science, 1992: 259-268.

[23] Black MJ, Sapiro G, Marimont DH, et al. Robust anisotropic diffusion [J]. IEEE Transactions on Image Processing, 1998, 7(3): 421-432.

[24] Tschumperle D. Fast anisotropic smoothing of multi-valued images using curvature-preserving PDE’s [J]. International Journal of Computer Vision, 2006, 68(1): 65-82.

[25] Vincken KL, Koster ASE, Viergever MA. Probabilistic multiscale image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(2): 109-120.

[26] Leung Y, Zhang JS, Xu ZB. Clustering by scalespace filtering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(12): 1396-1410.

[27] Petrovic A, Escoda OD, Vandergheynst P. Multiresolution segmentation of natural images: from linear to nonlinear scale-space representations [J]. IEEE Transactions on Image Processing, 2004, 13(8): 1104-1114.

[28] Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting [C] // Proceedings of SIGGRAPH 2000, 2000: 417-424.

[29] Bertalmio M, Bertozzi AL, Sapiro G. Navier-stokes, fl uid dynamics, and image and video inpainting [C] // Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001, 1: 355-362.

[30] Chan TF, Shen JH. Variational image inpainting [J]. Communications on Pure and Applied Mathematics, 2005, 58(5): 579-619.

[31] Serra J. Image Analysis and Mathematical Morphology [M]. Utah: Academic Press, 1982.

[32] Jackway PT, Deriche M. Scale-space properties of the multiscale morphological dilation erosion [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(1): 38-51.

[33] Guichard F, Moisan L, Morel JM. A review of P.D.E. models in image processing and image analysis [J]. Journal de Physique IV France, 2002, 12: 137-154.

[34] Lindeberg T. Edge detection and ridge detection with automatic scale selection [C] // Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1996: 465-470.

[35] Dolcetta IC, Ferretti R. Optimal stopping time formulation of adaptive image filtering [J]. Applied Mathematics and Optimization, 2001, 43(3): 245-258.

[36] Solo V. A fast automatic stopping criterion for anisotropic diffusion [C] // IEEE International Conference on Acoustics, Speech, and Signal Processing, 2002, 2: 1661-1664.

[37] Mrazek P, Navara M. Selection of optimal stopping time for nonlinear diffusion filtering [J]. International Journal of Computer Vision, 2003, 52(2-3): 189-203.

[38] Papandreou G, Maragos P. Image denoising in nonlinear scale-spaces: automatic scale selection via cross-validation [C] // IEEE International Conference on Image Processing, 2005: 1033-1036.

[39] Papandreou G, Maragos P. A cross-validatory statistical approach to scale selection for image denoising by nonlinear diffusion [C] // IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005: 625-630.

[40] Sun J, Xu ZB. Scale selection for anisotropic diffusion fi lter by Markov random fi eld model [J]. Pattern Recognition, 2010, 43(8): 2630-2645.

[41] Wen TX, Gu J, Zhang ZQ, et al. Scale selection for morphological top-hat transformation based on mutual information [C] // The 3rd International Congress on Image and Signal Processing, 2010(3): 1092-1096.

[42] Rigau J, Feixas M, Sbert M, et al. Medical image segmentation based on mutual information maximization [C] // MICCAI Lecture Notes in Computer Science, 2004, 3216: 135-142.

[43] Lu QW, Chen WF. Unsupervised segmentation of medical image based on difference of mutual information [J]. Science in China, Series F: Information Sciences, 2006, 49(4): 484-493.

[44] Lu ZT, Feng QJ, Shi PC, et al. Unsupervised segmentation of medical image based on FCM and mutual information [C] // IEEE International Conference on Complex Medical Engineering, 2007, 1: 513-516.

[45] Bezdek JC. Pattern Recognition with Fuzzy Objective Function Algorithms [M]. New York: Plenum Press, 1981.

[46] Gonzalez RC, Woods RE, Eddins SL. Digital Image Processing Using MATLAB [M]. Beijing: Publishing House of Electronics Industry, 2004.

[47] Chan T, Vese L. An active contour model without edges [J]. IEEE Transactions on Image Processing, 2001, 10: 266-277.

Image Denoising and Segmentation Based on Mutual Information Criterion

WEN Tiexiang1,2PAN Zhengyang1,3GU Jia1
1( Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )

2( University of Chinese Academy of Science, Beijing 100049, China )

3( University of Science and Technology of China, Hefei 230000, China )

Scalespace play an important role in many computer vision tasks. Automatic scale selection is the foundation of multi-scale image analysis, but its performance is still very subjective and empirical. To automatically select the appropriate scale for a particular application, a scale selection model based on information theory was proposed in this paper. The proposed model utilizes the mutual information as a measuring criterion of similarity for the optimal scale selection in multi-scale analysis, with applications to the image denoising and segmentation. Firstly, the multi-scale image smoothing and denoising method based on the morphological operator was studied. This technique does not require the prior knowledge of the noise variance and can effectively eliminate the changes of illumination. Secondly, a clusteringbased unsupervised image segmentation algorithm was developed by recursively pruning the Huffman coding tree. The proposed clustering algorithm can preserve the maximum amount of information at a speci fi c clustering number from the information-theoretical point of view. Finally, for the feasibility of the proposed algorithms, its theoretical properties were analyzed mathematically and its performance was tested through a series of experiments, which demonstrate that it yields the optimal scale for the developed image denoising and segmentation algorithms.

scale selection; mutual information; denoising; segmentation

TP 391

A

2013-11-20

温铁祥，博士研究生，研究方向为医学图像处理和计算机视觉；潘正洋，硕士研究生，研究方向为医学图像处理；辜嘉(通讯作者)，研究员，博士生导师，研究方向为计算机视觉和医学成像技术，E-mail：jia.gu@siat.ac.cn。