基于多尺度带限的自适应直方图均衡和数学形态学的医学 X 射线图像对比度增强算法

伍世宾 王 玥 谢耀钦

(中国科学院深圳先进技术研究院深圳518055)

基于多尺度带限的自适应直方图均衡和数学形态学的医学 X 射线图像对比度增强算法

伍世宾 王 玥 谢耀钦

(中国科学院深圳先进技术研究院深圳518055)

医学X射线图像是临床上应用最广泛的影像之一。由于需要采用低剂量的X射线进行成像，而X射线图像存在一个本质的缺陷，就是低对比度。所以，在临床应用中，往往需要对图像对比度进行增强处理。根据X射线图像特性，文章提出了基于多尺度带限的自适应直方图均衡和数学形态学的X射线图像对比度增强算法。首先，采用拉普拉斯高斯金字塔变换把图像分解成高频和低频的不同尺度子波段图像；然后对每塔层高频子图像应用对比度带限的自适应直方图均衡进行处理，相应的各塔层低通子图像使用数学形态学进行增强处理；最后，各塔层经过增强处理的高频和低频系数，通过拉普拉斯高斯金字塔的逆变换重构出对比度增强的图像。增强图像再经全局非线性算子进行对比度的增益调整，获得自然的视觉效果。实验结果表明该算法有效地增强了医学X射线图像的对比度，并通过图像对比度评价标准和对比度改进索引度量算法来分析及对比了算法的性能。

多尺度分析；数学形态学；拉普拉斯高斯金字塔；对比度增强

1 引 言

图像是信息可视化的重要手段。图像增强的主要目的是按照人们主观上、视觉上对理想图像的要求，对现存的图像进行后处理，以达到实际的应用要求。医学图像能以直观的形式给医生提供辅助诊断和治疗信息。特别对有经验的临床医生和放疗专家来说，他们能从这些图像中得到很多有用的信息。在数字X射线成像系统中，由于人体结构和组织的复杂性，以及受成像设备和获取条件等多种因素的影响，扫描出来的医学X射线图像质量较差，甚至出现伪迹、图像动态范围宽、对比度不高、边缘细节模糊等，这些都影响了医生和放疗物理师的临床诊断效率和准确性[1]。为了提高医生对人体某组织或器官的病灶区域的诊断准确率，常常需要对图像进行对比度增强的后处理，以增强图像的视觉效果，突出感兴趣对象区域或边缘。此外，由于医学图像的特殊性，改进图像质量应该以不丢失图像细节、不引入过大的噪声、避免导致细节失真为前提。因此，图像增强技术处理已经成为医学图像实际应用中不可或缺的一项工作。图像增强主要包括提高图像分辨率、提高图像对比度和信号分析方法。在医学图像处理中，单一像素运算或卷积算子很难满足实际的临床应用，各种图像增强技术的有机结合，已经成为图像增强研究的主流。

医学影像领域中，X射线被广泛用来获取人体内部某组织或器官的图像，有助于放疗师和临床医生识别人体内部的组织和器官。由于高剂量的X射线会对人体的正常组织和器官造成损伤，成像过程使用X射线的剂量较低，因此，X射线图像对比度低，人体组织和器官的边缘不清晰，这严重影响了医生对病人的正确诊断。Sundaram等[2]介绍了由于乳房X射线图像的对比度低，医生对乳癌的误诊率达10%。

传统的图像增强的方法主要有灰度变换、直方图均衡、直方图规定化、局部算子滤波器及反锐化掩膜等，其中，直方图均衡被广泛用于增强图像对比度强[3]。这些方法在增强图像的同时不可避免地放大了噪声。随着科学技术的快速发展，GPU技术被广泛应用于数据处理，计算机的计算能力越来越强大，涌现出许多针对某一模态的医学图像增强算法。而多尺度变换技术对图像进行分解与重构最为流行，并在医学图像增强应用中取得了很好的效果。目前，最常用的图像多尺度变换技术是拉普拉斯高斯金字塔变换和小波变换[4]。Lin等[5]和Wei等[6]陈述了基于自适应直方图和小波变换的算法，以用于X射线图像增强。Kother Mohideen等[7]使用了多小波和硬阈值方法对乳房X射线图像进行去噪和增强处理。Harish Kumar等[8]提出了基于形态学和小波变换的乳房X射线图像增强算法。Martin Stahl等[9]设计了基于拉普拉斯金字塔非线性多尺度方法，以用于数字X射线图像增强。然而，小波变换在增强复杂的组织或器官结构时会带来人为的伪影[4,10]。为了克服这一问题，我们的算法中的多尺度变换使用拉普拉斯高斯金字塔变换技术。我们提出的算法主要由三大部分组成：首先，利用拉普拉斯高斯变换把原X射线图像分解成不同尺度的高频和低频子图像；其次，使用对比度带限的自适应直方图均衡增强高频波段的系数，低通波段的子图像被数学形态学运算处理；最后，经过处理的高和低波段子图像通过拉普拉斯高斯逆变换重构出与原X射线图像大小相同的增强图像，再利用非线性的算子调整重构的增强图像的对比度。

2 材料与方法

2.1 多尺度图像变换

图1 多尺度分解流程图Fig.1. Flowchart of multiscale decomposition

多尺度分析方法是随着计算机视觉和图像处理技术的快速发展而产生和发展起来的新兴学科，有着严密的数学理论支撑，是一种应用非常广泛的方法，可以用于图像增强、分割和配准等。多尺度图像分解方法采用不同尺度下核函数模板卷积或插值的方式，对图像进行线性尺度空间信号分解[11]。传统的单一尺度的处理方法，无论是空间域还是频率域都是一种全局变换、全局处理，无法表达图像的时频、空间频域等性质[12]。多尺度图像分解过程具有可逆性，因此，使用有效、适当的系数运算算法或通过控制一系列增益系数，可以获得对原图像的增强效果。图像的线性尺度空间分解过程如图1所示。

图中 I0是原始输入图像，Gi(i＝0,1,2,3,…,N)为高斯滤波函数，“*”代表卷积运算，I0和G0进行卷积运算(即低通滤波处理)后产生0级图像I1，由此，

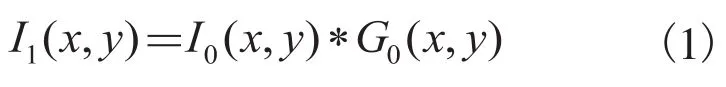
I1与输入图像I0的差，得到该级图像的信号残差D0：

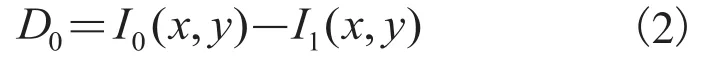
重复该过程，可以依次得到：

在图像分解过程中，Gi一般都采用低通滤波函数，这样中间过程得到的每一级图像Di是图像的高频信息，即是边缘和细节信息。换句话说，每次分解过程都可以看作为将待分解图像分解成高频和低频信息的过程，保存每一次分解得到的成分系数，就可以重构出原始输入图像，重构的图像可表示为：

因此，加上增强处理的重构结果可表示为：

式中(i＝0,1,2,3,…,N)是增强系数。

多尺度图像分解方法的逆过程如图2所示。

在本文中，我们采用拉普拉斯高斯金字塔变换作为多尺度分析算法。拉普拉斯高斯金字塔算法由Burt和Aedlson于1983年共同提出[4,10]。拉普拉斯高斯金字塔方法分解与重构图像的过程如图3所示。在多尺度每次分解过程中，所得到的图像均下采样为每次输入图像的 1/2。图3中↑代表下采样，↓代表上采样。塔型算法的具体描述如下：

图2 多尺度重构流程图Fig.2. Flowchart of multiscale reconstruction

图3 拉普拉斯高斯金字塔变换流程图Fig.3. Flowchart of the LapLacian Gaussian pyramid transform

输入图像经过高斯低通滤波和降采样获得g1(下一次分解的输入图像)，输入图像减去子图像 g1可以通过插值和卷积运算(上采样)产生与输入图像大小相同的图像的差得到b0，b0的生成过程等同于高通滤波处理，b0是图像的边缘和细节信息。重复该过程可以获得gk与bk层的子图像，直到获得最后一层子图像gL。重构过程如图3的右边部分所示。显然，对比度增强的过程出现在bL-1与b’L-1、gL与g’L之间。

2.2 带限自适应直方图均衡

直方图均衡是基于灰度运算的统计方法，也是最常用的直方图量化方法。直方图均衡是获得对比度增强的标准方法，它调整灰度级范围使其均匀分布，以累加变换函数分布为基础，产生一幅灰度分布具有均匀概率密度的增强图像。假设灰度级为L的数字图像，以图像中每个灰度级的象素值除以象素的总数得到图像归一化的灰度直方图，其离散函数定义如下：

式中，n 是图像总的像素数，nk是对应rk灰度层的像素数。

假设Pr(r)和Ps(s)分别是原图像和均衡后的图像的概率密度函数，根据直方图的定义和累计密度函数，可得到公式：

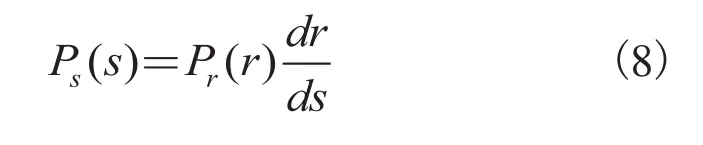
假设0sL—1，根据直方图函数与灰度变换函数可推导出公式：

通常，公式(9)是灰度映射函数。

目前，根据实际应用要求，有很多改进的直方图算法，如修正直方图均衡、自适应直方图均衡和带限的自适应直方图均衡等。本文根据医学X 射线图像的特性采用了对比度带限的自适应直方图均衡处理高频系数，这不但可有效增强图像的对比度，而且极大地限制了噪声的放大。

2.3 数学形态学

数学形态学起源于集合理论，也称图像代数，是以形态为基础对图像进行分析的数学工具[13]。形态运算的基本思想是用具有一定形态的结构元素去量度和提取图像中的对应形状，达到图像分析和识别的目的。形态学以膨胀和腐蚀基本运算为基础，引出了其它常用的开、闭运算等。开运算和闭运算都能平滑图像的轮廓，其中，根据形态的结构元素大小，开运算是削弱狭窄的部分，去掉孤立点，而闭运算一般可融合缺口和细长的部分，填补轮廓上的缝隙，去掉小洞。开、闭运算的分别由公式(10)和公式(11)所示：

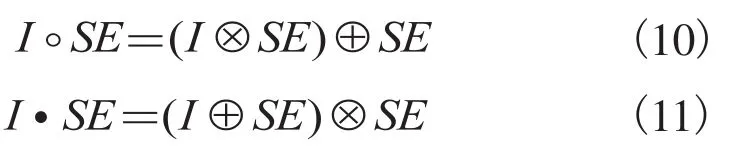
式中，I 代表输入图像，SE 是结构元。

在实际图像处理应用中，形态学的开与闭运算是配对使用来达到目的，常用的两种形态学运算的组合是顶帽(Top-hat,HT)和底帽(Bottom-hat, BH)变换，其运算公式分别如(12)和(13)所示。

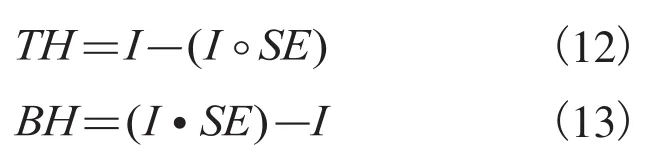
由上可有，TH 变换可以有效地增强小细节信息，与之对应，BH变换可以丰富特征、纹理信息。为了增强X射线图像的局部对比度，我们同时利用了 TH 和 BH 变换，其计算公式如(14)所示。

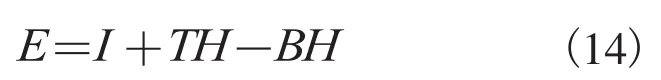
2.4 方法原理

传统的图像增强技术不能自适应复杂特征的图像。全局变换或调整算子的图像增强算法往往会得到不理想的结果，至少图像内的局部特征和细节信息得不到凸显。为了解决此问题，我们提出了基于多尺度带限的自适应直方图均衡和数学形态学的医学X射线图像对比度增强算法，该方法不但可以增强边缘和局部细节信息，而且有效抑制了噪声的放大。算法的实施过程如下描述：

首先，采用拉普拉斯高斯金字塔变换把输入图像分解成不同尺度的高频和低频的子图像。目前，各种图像滤波技术，包括灰度算子、中值滤波、边缘增强算子、频域增强算子、空间频域滤波器和各向异性自适应融合滤波器等，都是通过去噪以达到增强的效果。然而，这些技术适合图像全局特征增强。在医学影像的临床应用中，往往需要增强图像中局部特征和边缘。而数学形态学运算可以满足此要求。因此，我们使用数学形态学运算处理所有塔层的低通子图像，以增强图像对比度，丰富图像信息、压制噪声、平滑图像。

其次，直方图均衡可以丰富图像的细节信息和锐化边缘，图像的细节和边缘信息是高频成分，而且，高频波段也包含噪声。因此，我们采用带限的自适应直方图均衡增强高频子波段系数，不但可以增强特征信息、图像对比度和丰富细节信息与图像边缘，而且有效地压制了噪声的放大。与自适应直方图均衡相比，带限的自适应直方图均衡提高了计算效率，实现噪声可控。而与传统直方图均衡和修正直方图均衡相比较，带限的自适应直方图均衡可以更好地增强局部特征、边缘和对比度。

最后，由于拉普拉斯高斯金字塔变换具有可逆性，我们利用其逆变换把分别被带限的自适应直方图均衡和数学形态学处理的高频、低频系数，来重构出与输入图像相同大小的增强图像。此外，采用了一个全局非线性的增益调整算子对其进行处理，使得增强图像更加自然和平滑。本文算法的框架如图 4 所示。

图4 本文算法的流程图Fig.4. Flowchart of the proposed method

3 实验与结果分析

本文分别使用了5幅胸片X射线影图(来源：谷歌图片搜索)和5幅乳房X射线影像(来源：深圳安健医疗器设公司)来测试提出算法的可靠性和稳定性，本文中实验结果只展示了其中各一幅的增强结果，算法的实施、执行在MatLab2012a。通过把实验结果与基于拉普拉斯非线性多尺度处理方法[9]的结果作比较，来验证提出算法的先进性和临床的实用价值。而算法的优越性和鲁棒性等则通过视觉效果和性能度量指标两个方面来分析和评价。

3.1 对比度评价标准

Sundaram[14]提出了图像对比度的计算方法，其计算公式如下：

式中，M和N分别为图像的长和宽，是增强的图像，公式(15)的值越大表明图像的对比度越好。

3.2 对比度改进因子

对比度增强的量化度量可以用对比度改进因子来描述，其公式如下表示[15-19]：

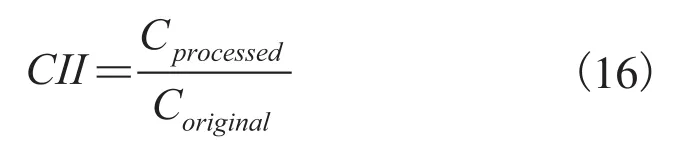
式中，和分别是增强图像和原始图像。C是局部区域对比度的平均值，因此，原始图像的CII值等于1。在局部窗口中，每个像素局部对比度的计算是(Xmax—Xmin)／(Xmax+Xmin)。我采用了最优化的对比度计算方法，其计算公式如下表示：

式中，mf是前景亮度均值，相应的mb是背景亮度均值。在实验中，我们使用5×5的局部窗口。CII 的值越大表示图像的质量越好。

如图5所示，本文算法有效地改进胸片X射线图像的对比度，增强和保护了图像的细节、边缘信息。胸片X射线图像中脊椎内的金属丝变得清晰可见，胸部肋骨显著增强，视觉效果良好。然而，基于拉普拉斯金字塔非线性多尺度算法对胸片X射线图像的对比度虽有所改进，增强图像很平滑，但图像的细节、边缘很模糊，且不清晰，视觉效果差，影响临床医生的视觉诊断。

根据表1描述，本文算法在增强对比度和对比度改进因子都优与基于拉普拉斯金字塔非线性多尺度算法。依据度量结果的分析，本文算法更适合用于增强胸片X射线图像的对比度。

如图6所示，本文算法有效地改进了乳房X射线图像的对比度，增强和保护了图像的细节、边缘信息，乳房X射线图像中腺体、结节变得清晰可见，视觉效果好，具有重要的临床诊断意义。然而，基于拉普拉斯金字塔非线性多尺度算法对乳房X射线图像的对比度虽有所改进，增强图像很平滑，但图像的细节、边缘很模糊，且不清晰。在某种程度上，图像出现了白化现象，视觉效果差，很难用于临床的视觉诊断。

表1 胸片X射线增强图像对比度和对比度改进因子的度量Table1. Enhancement evaluation of contrast and contrast improved index for Fig.5

图6 乳房X射线图像对比度增强比较Fig.6. Comparison of the enhanced mammogram contrast

表2数据显示，本文算法在增强乳房X射线图像对比度和对比度改进因子都优于基于拉普拉斯金字塔非线性多尺度算法。由于深圳安健医疗器设公司扫描的乳房图像是使用16位的平板探测器，因此，图像增强的计算空间大，获得良好的度量结果。依据度量的结果分析，并与基于拉普拉斯金字塔非线性多尺度算法相比较，本文算法更有效地增强了乳房X射线图像的对比度。

表2 乳房X射线增强图像对比度和对比度改进因子的度量Table2. Enhancement evaluation of contrast and contrast improved index for Fig.6

4 结 语

针对医学X射线图像的特点，我们提出了一种基于多尺度带限自适应直方图均衡和数学形态学的医学X射线图像对比度增强算法。算法严格控制局部对比度增强，防止增强过程放大噪声。因此，本文算法在有效增强图像对比度的同时也抑制了噪声的放大，增强的X射线图像在临床实践中起到了有意义的作用。但是，增强的图像仍存在不足，在视觉效果上不够自然。在未来的研究中，我们将进一步改进算法，同时，使用乳房X射线图像的标准数据库中的图像测试和验证本文算法的鲁棒性、稳定性等，把实验结果与目前最新的医学X射线图像增强算法进行比较，采用更多的度量指标衡量算法性能的优越性。

[1] 罗述谦, 周果宏. 医学图像处理与分析 [M]. 北京:科学出版社, 2003: 38-64.

[2] Sundaram M, Ramar K, Arumugam N, et al. Histogram based contrast enhancement for mammogram images [C] // Proceedings of 2011 International Conference on Signal Processing, Communication, Computing and Networking Technologies, 2011: 842-846.

[3] Rathi MS, Karode AH, Suralkar SR. Contrast enhancement and smoothing using histogram modification method [J]. International Journal of Computer Technology and Application, 2012, 3(5): 1789-1798.

[4] Dipple S, Stahl M, Wiemker R, et al. Multiscale contrast enhancement for radiographies: Laplacian pyramid versus fast wavelet transform [J]. IEEE Transactions on Medical Imaging, 2002, 21(4): 343-353.

[5] Lin J, Wei WY, Wang L, et al. Industrial X-ray image enhancement algorithm based on adaptive histogram and wavelet [C] // The 6th International Forum on Strategic Technology, 2011: 836-839.

[6] Wei J, Wang DD, Wang YW, et al. Industrial X-ray image enhancement algorithm based on AH and MSR [J]. Scientif i c Research, 2011, 3: 1040-1044.

[7] Mohideen K, Perumal A, Krishnan N, et al. Image denoising and enhancement using multiwavelet with hard threshold in digital mammographic images [J]. International Arab Journal of e-Technology, 2012, 2(1): 49-55.

[8] Kumar NH, Amutha S, Babu R. Enhancement of mammographic images using morphology and wavelet transform [J]. Computer Technology Application, 2012, 3(1): 192-198.

[9] Stahl M, Dippel S. Digital radiography enhancement by nonlinear multiscale processing [J]. Medical Physics, 2000, 27(1): 56-65.

[10] Burt PJ, Adelson EH. The Laplacian pyramid as a compact image code [J]. IEEE Transactions on Communications, 1983, 31( 4): 532-540.

[11] 张敏, 牟轩沁. 一种多尺度X射线胸片图像增强算法[J].西安交通大学学报,2010,44:83-87.

[12] 何祥彬. DR 的计算机控制与图像增强方法研究 [D].合肥: 中国科学技术大学, 2010.

[13] 赵月萍. X 射线图像动态降噪技术的研究 [D]. 太原: 中北大学, 2011.

[14] Sundaram M, Ramar K, Arumugam N, et al. Histogram modif i ed local contrast enhancement for mammogram images [J]. Applied Soft Computing, 2011, 11(8): 5809-5816.

[15] Morrow WM, Paranjape RB. Region-based contrast enhancement of mammograms [J]. IEEE Transactions on Medical Imaging, 1992, 11(3): 392-406.

[16] Laine A, Fan J, Yang WH. Wavelets for contrast enhancement of digital mammography [J]. Engineering in Medicine and Biology Magazine, 1995, 14(5): 536-550.

[17] Laine A, Hud W, Steinbach B, et al. Mammographic image processing using wavelet processing techniques [J]. European Radiology, 1995, 5(5): 518-523.

[18] Trivedi M, Jaiswal A, Bhateja V. A new contrast improvement index based on logarithmic image processing model [J]. Advances in Intelligent System and Computing, 2013, 199: 715-723.

[19] Sakellaropoulos P, Costaridou L, Panayiotakis G. A wavelet-based spatially adaptive method for mammographic contrast enhancement [J]. Physics in Medicine and Biology, 2003, 48(6): 787-803.

Contrast Enhancement of Medical X-ray Images Based on Multiscale Limited Adaptive Histogram Equalization and Mathematical Morphology

WU Shibin WANG Yue XIE Yaoqin
( Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )

The medical X-ray image is one of the images most widely applied in clinical applications. Because the lowdose X-ray image needed for imaging is of a low contrast, the X-ray image contrast enhancement is processed before the clinical application. A new algorithm for contrast enhancement of mammographic images was proposed in this paper. The approach was based on the multiscale transform and mathematical morphology. First of all, the Laplacian Gaussian pyramid operator was applied to transform the image into different scale sub-band images. In addition, the high-frequency subimages were equalized by contrast limited adaptive histogram equalization and low-pass sub-images were processed by the mathematical morphology. Finally, the image of enhanced contrast was reconstructed from the Laplacian Gaussian pyramid coeff i cients of high or low frequencies modif i ed by contrast limited adaptive histogram equalization and mathematical morphology respectively. The enhanced image was processed by a global non-linear operator. The experimental results show that the proposed algorithm is effective for the contrast enhancement of the medical X-ray image. The performances of the proposed algorithm were measured by contrast evaluation criterion for image and contrast improvement index.

multiscale analysis; mathematical morphology; Laplacian Gaussian pyramid; contrast enhancement

Q 334

A

2013-11-20

国家自然科学基金(51105359 及 61072031)、国家高技术研究发展计划(863计划)(2012AA02A604)、国家重点基础研究发展计划(973计划)子课题(2010CB732606)。

伍世宾，博士研究生，研究方向为医学图像处理；王玥，硕士，研究助理，研究方向为生物医学电子学与图像处理；谢耀钦(通讯作者)，博士，研究员，研究方向为医学影像，E-mail：yq.xie@siat.ac.cn。