Measurement and Correlation of Vapor-Liquid Equilibrium of the 1,2-Epoxycyclohexane-Cyclohexanone Binary System at 101.3 kPa*
WANG Xunqiu (王训遒), ZHUANG Xinliang (庄新亮)2and JIANG Denggao (蒋登高)
1School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001, China
2Wanhua Chemical Group Co., Ltd., Yantai 264002, China
Measurement and Correlation of Vapor-Liquid Equilibrium of the 1,2-Epoxycyclohexane-Cyclohexanone Binary System at 101.3 kPa*
WANG Xunqiu (王训遒)1,**, ZHUANG Xinliang (庄新亮)1,2and JIANG Denggao (蒋登高)1
1School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001, China
2Wanhua Chemical Group Co., Ltd., Yantai 264002, China
Many by-products are generated in the process of oxidizing cyclohexene to produce 1,2-epoxycyclohexane by hydrogen peroxide, including cyclohexanol, cyclohexanone, etc. To obtain high-purity 1,2-epoxycyclohexane, the by-products must be removed through rectification. Refining 1,2-epoxycyclohexane through rectification requires vapor-liquid equilibrium (VLE) data of the related system. Therefore, the VLE data of 1,2-epoxycyclohexanecyclohexanone system were measured at 101.3 kPa using an improved EC-2 VLE still. The thermodynamic consistency of the data was then tested by Herington’s method and the rigorous point-to-point method. The results obtained were exemplary. The VLE data were correlated by the Wilson and non-random two-liquid (NRTL) equations, using the error sum squares of the vapor composition as the objective function to obtain the model parameters. The difference between the calculated values and the experimental data is minor, indicating that the VLE data are suitable for engineering design. Keywords vapor-liquid equilibrium, 1,2-epoxycyclohexane, cyclohexanone, Wilson equation, NRTL equation
1 INTRODUCTION
The oxidation of olefins has been widely studied worldwide [1-3]. Many by-products, such as cyclohexanol (CAS Registry No. 108-93-0), cyclohexanone (CAS Registry No. 108-94-1), 1,2-cyclohexanediol (CAS Registry No. 1460-57-7), and others [4], are generated during the process of oxidizing cyclohexene (CAS Registry No. 110-83-8) with hydrogen peroxide (CAS Registry No. 7722-84-1) to synthesize 1,2-epoxycyclohexane (CAS Registry No. 286-20-4). Rectification under normal atmospheric pressure is one of the most commonly used processes in removing by-products in order to obtain high purity 1,2-epoxycyclohexane. The VLE data of the relevant systems (1,2-epoxycyclohexane, cyclohexanol, cyclohexanone, et al.) are essential in designing the rectification process. Literature shows that only 1,2-epoxycyclohexane-cyclohexene [5] and cyclohexanol-cyclohexanone [6] binary systems have been investigated. In this work, the vapor-liquid equilibrium (VLE) data of the 1,2-epoxycyclohexane-cyclohexanone system at 101.3 kPa using an improved EC-2 VLE still are tested and discussed.
2 EXPERIMENTAL
2.1 Materials and apparatus
The chemicals used were 1,2-epoxycyclohexane and cyclohexanone. Analytical reagent grade 1,2-epoxycyclohexane (mass fraction purity≥0.995, normal boiling point 404.52 K) was synthesized and purified through multi-rectifications. Analytical reagent grade cyclohexanone (mass fraction purity≥0.995) was purchased from Sinopharm Chemical Reagent Co., Ltd., and further purified through rectification. Normal boiling points and Antoine constants of the two substances are shown in Table 1 for reference.
The apparatus [9] employed was an improved EC-2 VLE still made by Tianjin University. Validation of the apparatus showed that the improved EC-2 VLE still had very good precision in obtaining the VLE data [9].Three calibrated mercury microthermometers (i.e., 273.15-323.15 K, 373.15-423.15 K, and 423.15-473.15 K) were used. A vapor sampler and a liquid sampler were used to collect the samples periodically. A gas chromatograph (GC-900A) with a flame ionization detector (FID) detector and SE-54 GC column (Φ0.53 mm×1.0 µm×30 m, 5% phenyl+ 95% dimethyl polysiloxane), manufactured by Shanghai Kechuang Chromatography Instrument Co., Ltd., was used to determine the compositions of the samples. The pressure in the apparatus was maintained at 101.33 kPa with the help of a pressure control system consisting of one U-tube manometer, one mercury barometer (for measuring air pressure), one regulator valve, one air pump, one buffer tank, and one regulator valve.
The measurements reported in the present study were expected to be accurate within ±0.1 K in temperature, and ±100 Pa in pressure.

Table 1 Boiling point at 101.3 kPa (Tb) and Antoine constant (A, B, C) of 1,2-epoxycyclohexane(1) and cyclohexanone(2)
2.2 Procedure
Firstly, a certain amount of the 1,2-epoxycyclohexane-cyclohexanone solution was placed in the improved EC-2 VLE still. The solution was then heated to reflux at 20-30 drops per minute by adjusting the heating coil voltage using a variable voltage transformer. The vapor-liquid system was assumed to have attained equilibrium after the temperature of the solution remained constant for 4-4.5 h. Secondly, the samples of the vapor and liquid were taken out by two sampler respectively, and their composition were determined by GC. Thirdly, a given mass of the 1,2-epoxycyclohexane-cyclohexanone solution was drawn out from the still by a syringe and the same volume of 1,2-epoxycyclohexane was injected to the VLE still. Finally, the same operation was repeated.
2.3 Sample analysis
The sample was analyzed using a temperature programming GC method. The analytical conditions were as follows: the column temperature was initially set to 328.15 K and heated at a rate of 3 K·min−1to 348.15 K; the vaporizer and the detector temperatures were set to 463.15 K; the carrier gas was nitrogen with a flow rate of 30 ml·min−1; the hydrogen flow rate was 30 ml·min−1; the air flow rate was 300 ml·min−1; and each of the two injected samples was 0.02 µl.
As the sample contained the two components of 1,2-epoxycyclohexane and cyclohexanone only, a set of 1,2-epoxycyclohexane plus cyclohexanone reference solutions of different concentrations was prepared to obtain the peak area fraction of 1,2-epoxycyclohexane through chromatographic analysis. Afterwards, a standard correlation curve was drawn (Fig. 1) to show the correlation between the mass fraction of 1,2-epoxycyclohexane and the abscissas of the peak area fraction of 1,2-epoxycyclohexane in order to determine the mass fraction of 1,2-epoxycyclohexane in the sample. Finally, the composition was converted into mole fraction.
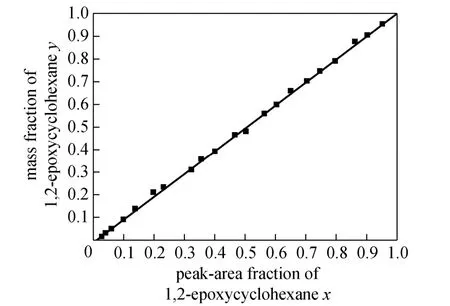
Figure 1 Calibration trace of mass fraction of 1,2-epoxycyclohexane
3 RESULTS AND DISCUSSION
3.1 Experimental data
With the improved EC-2 VLE still, the VLE data of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) system were measured in the temperature range of 404.52-428.82 K at a normal pressure of 101.3 kPa,. The results are shown in Table 2.
3.2 Thermodynamic consistency test
The VLE data of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) system were measured at 101.3 kPa, and thus the vapor phase was treated as an ideal gas [10]. The VLE equation can be simplified as follows:
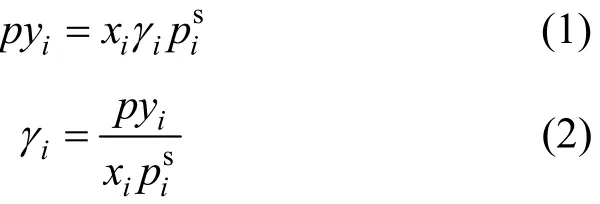
where
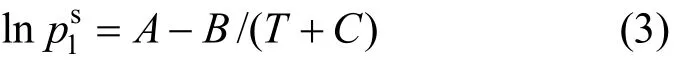
and
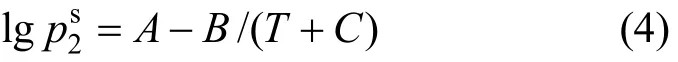
The values of the liquid activity coefficient were calculated and are shown in Table 2.
The test for the thermodynamic consistency of the VLE data is to check the reliability of the experimental data by applying the thermodynamic general formula. The basic formula is the Gibbs-Duhem equation, which can test the fugacity correlation of all the components in the mixture. Herrington’s equal-area method was used to test the thermodynamic consistency of the experimental data. The method was implemented as follows:
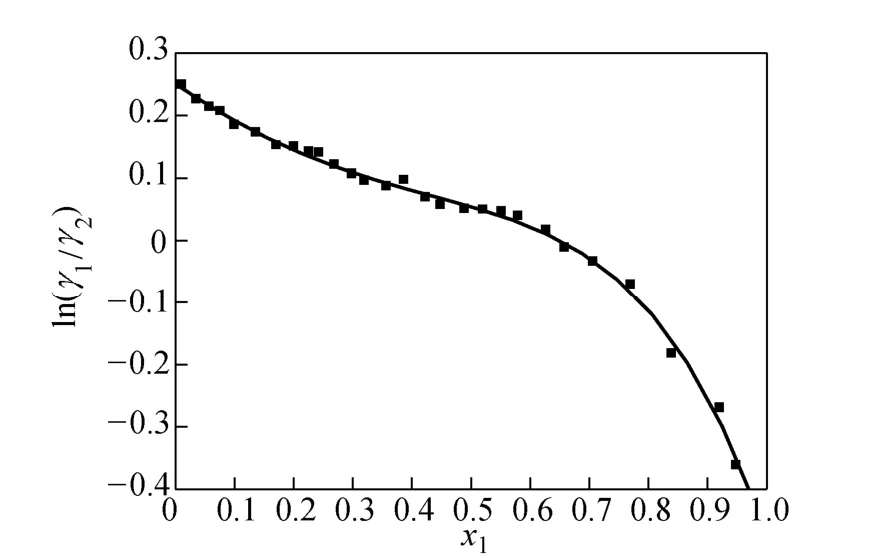
Taking in12/γ γ as the ordinate and χ1as the abscissas, the curve is given as shown in Fig. 2:
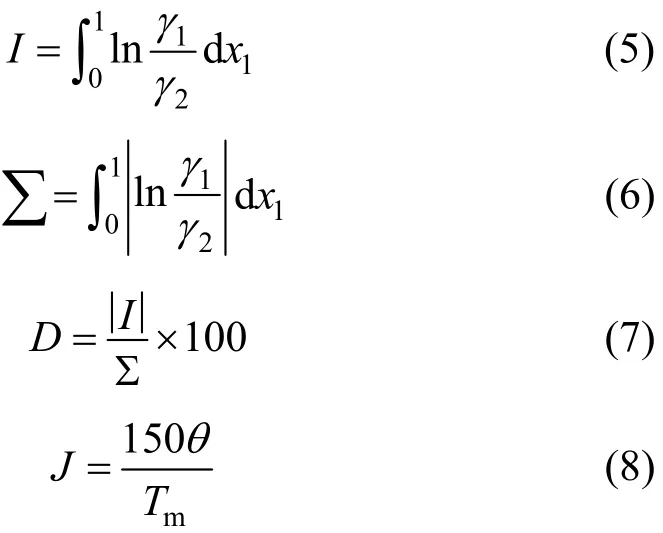
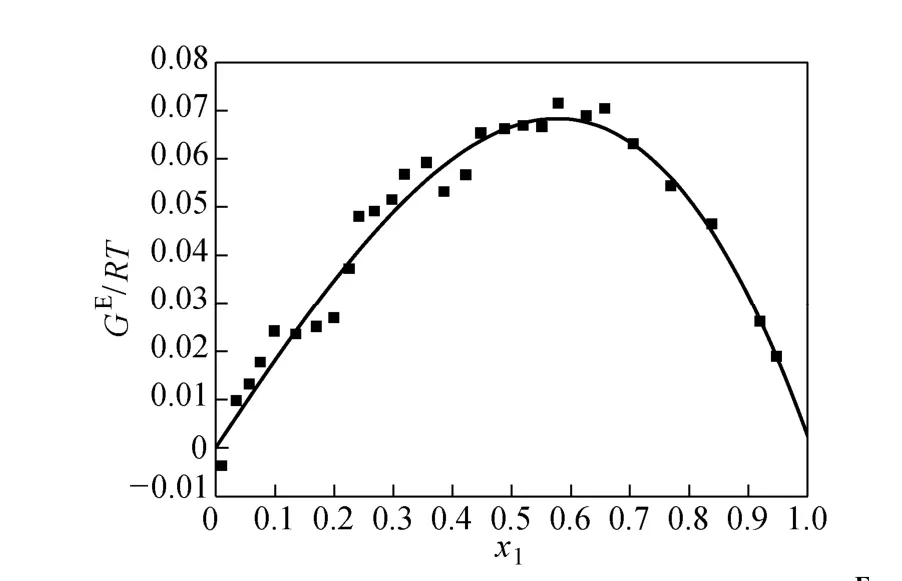
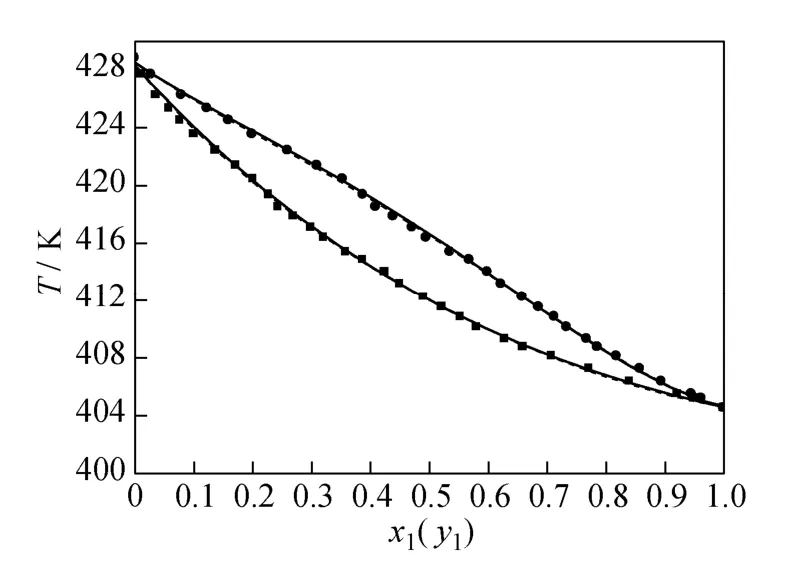
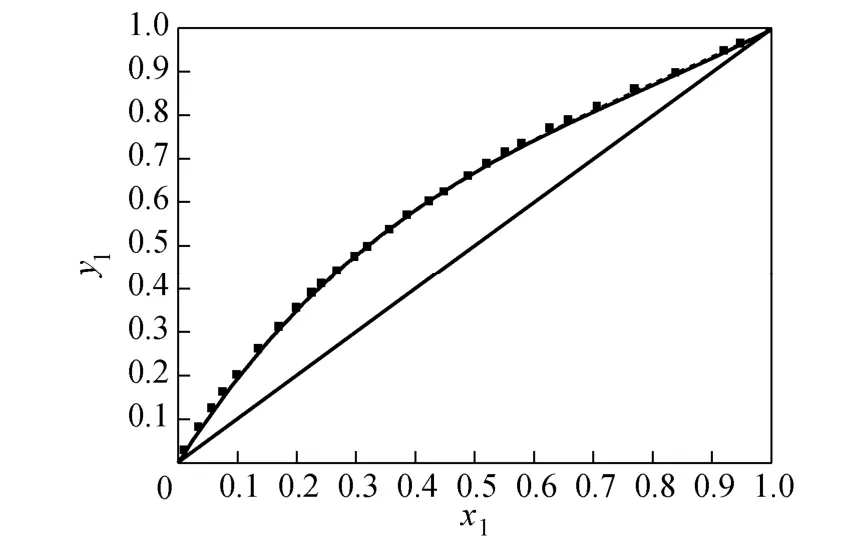
where Tmis the minimum boiling point of the system, 150 is an empirical constant given by Herrington after the enthalpy of mixing several typical organic solutions was analyzed; and θ is the difference between the boiling points of the different components in the system. In the present case, θ=428.80−404.87= 23.93 K. If an azeotrope is generated, θ is equal to thedeviation value between the lowest azeotropic temperature and the highest boiling point, or between the highest azeotropic temperature and the lowest boiling point [10]. The assessment criterion was provided by Herington, i.e., if D Table 2 System temperature (T), measured liquid-phase mole fractionof 1,2-epoxycyclohexanemeasured va-por-phasemole fraction of 1,2-epoxycyclohexaneabsolute deviation (|Δy|), absolute temperature deviation (|ΔT|),and liquid-phase activity coefficients (γ1 and γ2) of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) binary system at 101.3 kPa from 404.52-428.82 K Table 2 System temperature (T), measured liquid-phase mole fractionof 1,2-epoxycyclohexanemeasured va-por-phasemole fraction of 1,2-epoxycyclohexaneabsolute deviation (|Δy|), absolute temperature deviation (|ΔT|),and liquid-phase activity coefficients (γ1 and γ2) of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) binary system at 101.3 kPa from 404.52-428.82 K ①; ② ? Figure 2 Diagram of χ1versus ln(γ1/γ2) Based on Fig. 2, I=0.0113, Σ=0.1327, D=8.49, and J=8.87. Since D The curve of excess Gibbs energy function (GE/RT) versus χ is shown in Fig. 3. The thermodynamic consistency of the VLE data with the rigorous point-to-point method of Fredenslund is checked, andthe results show that the maximum variation (Δy1) between the calculated and the experimental data is 0.006 with an average variation of only 0.002. As the variation is less than 0.01, the experimental data is shown to be thermodynamically consistent [12]. Figure 3 The curves of excess Gibbs energy function (GE/RT) versus χ1 3.3 Correlation of experimental data Liquid activity coefficient can be correlated with the Wilson and NRTL equations. The activity coefficients (γ1and γ2) for the Wilson equation [13] are where The activity coefficients for the NRTL equation [14] are where The objective function is chosen for where the subscript “cal” represents the calculated value, and the subscript “exp” represents the experimental data. Through nonlinear regression analysis, Wilson parameters λ12−λ11=1637.53 J·mol−1and λ21−λ22=−3741.92 J·mol−1, and NRTL parameters J·mol−1, and α=0.2(α12=α21) were obtained. These parameters were further used to calculate the activity coefficients of 1,2-epoxycyclohexane and cyclohexanone. Subsequently, the vapor phase compositions corresponding to different temperatures were computed. The results are shown in Table 2. As presented in Table 2, when the calculated values by the Wilson and NRTL parameters match the experimental data, the average value of the absolute deviation (|Δy|) is 0.0034 and 0.0040, and the average value of the absolute temperature deviation (|ΔT|) is 0.13 K and 0.15 K, respectively. Hence, the Wilson and NRTL equations can be used to correlate the 1,2-epoxycyclohexane and cyclohexanone binary system at 101.3 kPa, meeting the requirement of engineering design. The experimental and calculated values by the Wilson and NRTL equations of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) system at 101.3 kPa are presented in Figs. 4 and 5, respectively.J·mol−1, Figure 4 Experimental and calculated T-y1-χ1diagram of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) system at 101.3 kPa The VLE data of the 1,2-epoxycyclohexanecyclohexanone system were measured at 101.3 kPa using an improved EC-2 VLE still. The Herrington equal-area method and the rigorous point-to-point method were used to test the thermodynamic consistency of the experimental data, which showed excellent consistency. Figure 5 Experimental and calculated y1-χ1diagram of the 1,2-epoxycyclohexane(1)-cyclohexanone(2) system at 101.3 kPa The VLE data correlated with the Wilson and NRTL equations, taking the sum of the error squares of vapor phase composition as the objective function to obtain model parameters λ12−λ11=1637.53 J·mol−1,=−3631.17 J·mol−1, α=0.2. The andaverage values of the absolute deviation are minor. Therefore, the Wilson and NRTL equations can be used to correlate the 1,2-epoxycyclohexane and cyclohexanone binary system at 101.3 kPa, and the results can meet the requirements of engineering design. NOMENCLATURE A, B, C Antoine constant F objective function GEexcess Gibbs energy, J·mol−1 gji−giiNRTL interaction energy between i and j, J·mol−1 n number of experiments p system pressure, kPa pssaturation vapor pressure, kPa R gas constant, J·mol−1·K−1 T temperature, K χiliquid mole fraction of component i yivapor mole fraction of component i α non-randomness parameter in NRTL equation γiactivity coefficient of component i Λ12, Λ21parameters of the Wilson equation λij−λjjWilson interaction energy between i and j, J·mol−1 Superscripts cal calculated data exp experimental data Subscripts b normal boiling point i, j components in a mixture or data points REFERENCES 1 Serwicka, E.M., Poltowicz, J., Bahranowski, K., Olejniczak, Z., Jones, W., “Cyclohexene oxidation by Fe-, Co-, and Mn-metallporphyrins supported on aluminated mesoporous silica”, Appl. Catal. A: Gen., 275 (1), 9-14 (2004). 2 Chang, Y., Lv, Y., Lu, F., Zha, F., Lei, Z.Q., “Efficient allylic oxidation of cyclohexene with oxygen catalyzed by chloromethylated polystyrene supported tridentate Schiff-base complexes”, J. Mol. Catal. A: Chem., 320, 56-61 (2010). 3 Salavati-Niasari, M., “Host (nanocage of zeolite-Y)/guest (manganese(II), cobalt(II), nickel(II) and copper(II) complexes of 12-membered macrocyclic Schiff-base ligand derived from thiosemicarbazide and glyoxal) nanocomposite materials: Synthesis, characterization and catalytic oxidation of cyclohexene”, J. Mol. Catal. A: Chem., 283, 120-128 (2008). 4 Wang, X.Q., Zhuang, X.L., Qin, X.Y., Wang, H., Jiang, D.G., Chen, J.B., “Study on the distillation process of 1,2-epoxycyclohexane”, Journal of Zhengzhou University (Engineering Science), 32 (2), 23-25 (2011). 5 Wang, X.M., Jiang, D.G., Geng, Z.X., “Measurement and correlation of vapor liquid equilibrium data for cyclohexene-1,2-epoxycyclohexane binary system under normal pressure”, J. Chem. Eng. Chinese Uni., 23 (3), 365-368 (2009). 6 Zeng, Y.L., Yang, Y.Q., Luo, H.A., Duan, Z.K., Liu, W.Y., “Vapor-liquid equilibria for the ternary systems of cyclohexanol, cyclohexanone and diglycol”, Chem. Eng. (China), 35 (6), 34-36 (2007). 7 Schilt, M.A.V., Wering, R.M., Kemmere, M.F., Loos, T.W.D., Keurentjes, J.T.F., “Measurement and modeling of the high-pressure phase behavior of the binary system carbondioxide+1,2-epoxyclohexane”, J. Chem. Eng. Data, 50 (6), 1879-1882 (2005). 8 Goodwin, S.R., Newsham, D.M.T., “Relative volatilities of mixtures of cyclohexanol and cyclohexanone in pressure range 30-750 mm mercury”, J. Chem. Eng. Data, 19 (4), 363-366 (1974). 9 Wang, X.Q., Zhuang, X.L., Yun, S.S., Chen, J.B., Jiang, D.G.,“Measurement and correlation of vapor-liquid equilibrium for a cyclohexene-cyclohexanol binary system at 101.3 kPa”, Chin. J. Chem. Eng., 19 (3), 484-488 (2011). 10 Chen, Z.X., Gu, F.Y., Hu, W.M., Chemical Engineering Thermodynamics, 2nd edition, Chemical Industry Press, Beijing, 177-179 (2000). (in Chinese) 11 Gao, G.H., Tong, J.S., Chemical Engineering Thermodynamics, 2nd edition, TsingHua University Press, Beijing, 337-339 (2007). (in Chinese) 12 Fredenslund, A., Gmehling, J., Rasmussen, P., Vapor-Liquid Equilibria Using UNIFAC a Group-contribution Method, Elsevier Scientific Publishing Co., Amsterdam (1977). 13 Wilson, G.M., “Vapor-liquid equilibrium. XI. A new expression for the excess energy of mixing”, J. Am. Chem. Soc., 86 (2), 127-130 (1964). 14 Renon, H., Prausnitz, J.M., “Local compositions in thermodynamic excess functions for liquid mixtures”, AIChE J., 14 (1), 135-144 (1968). CHEMICAL ENGINEERING THERMODYNAMICS Chinese Journal of Chemical Engineering, 22(3) 355—359 (2014) 10.1016/S1004-9541(14)60042-2 2012-03-01, accepted 2012-09-20. *Supported by the Key Scientific and Technology Project of Henan Province (132102210050). **To whom correspondence should be addressed. E-mail: wxqiu@zzu.edu.cn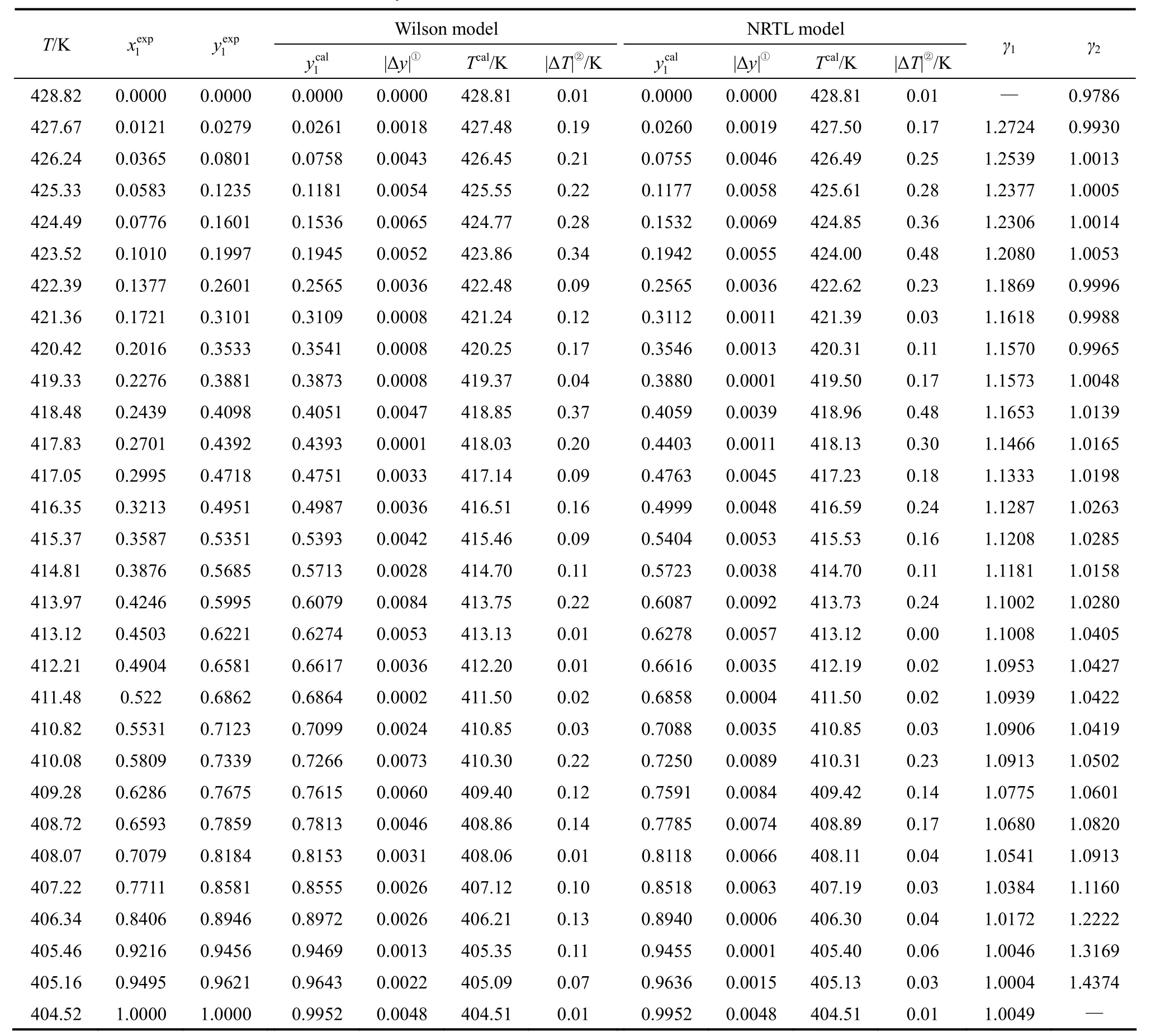
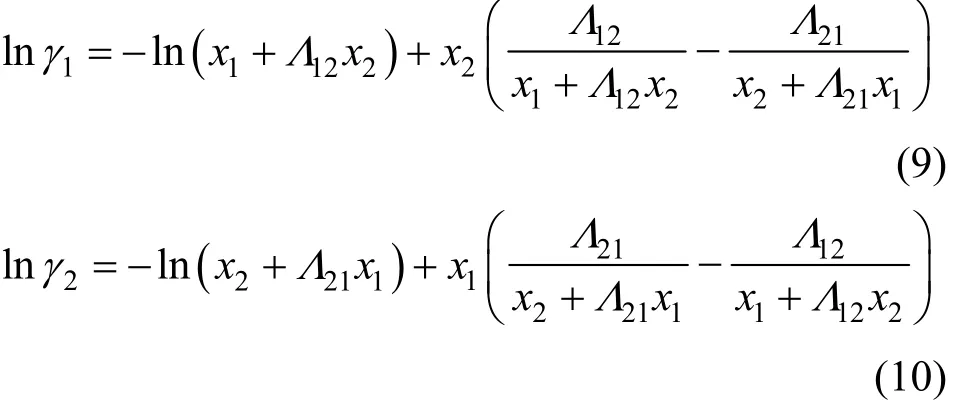
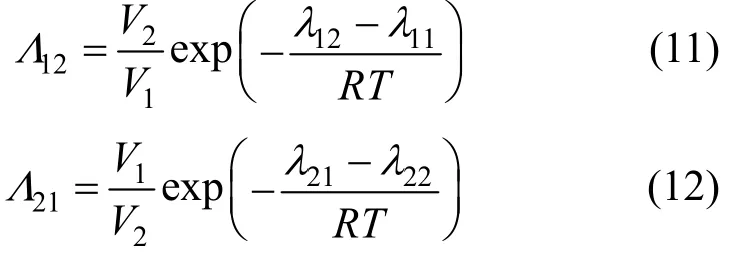
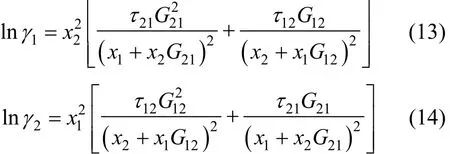
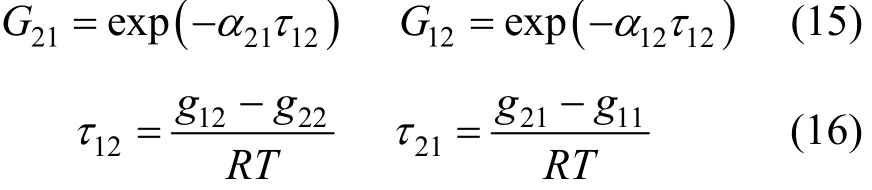
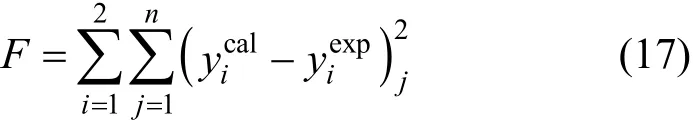
4 CONCLUSIONS
 Chinese Journal of Chemical Engineering2014年3期
Chinese Journal of Chemical Engineering2014年3期
