基于过度自信和努力水平的委托代理模型

李 聪

(天津大学管理与经济学部，天津300072)

1 文献综述

经济生活中人们总是表现出过度自信的倾向，表现为过高地估计自身的知识、能力水平［1］，过高地估计所掌握信息的准确性［2］。研究表明，管理者和企业家都存在过度自信［3－4］。BUSENITZ等［5］的研究得出了委托人和代理人都存在过度自信的结论。GERVARIS等［6］将过度自信定义为:认为自己所掌握的信息或知识的准确性比事实程度更高的一种信念，即对自己所掌握信息赋予权重大于事实的权重。

国外基于过度自信的委托代理理论研究取得了不少成果。GERVARIS等［7］认为，自信管理者比他们的同行企业更具有吸引力，因为理性的过度自信，他们努力学习更多的项目。SCHRAND等［8］通过对49家公司的分析得出结论:过度自信的高管更容易表现出乐观的偏见，从而更容易开始走下坡路，导致越来越多的故意错报。BOLTON等［9］发现股东们更青睐的不是更理性的，而是过度自信水平相对较差但能力较强的CEO，这更能增大股东的利益，增加公司的价值。KEIBER［10］和 ROSA［11］分别对具有相同和不同过度自信水平的委托人和代理人的工资契约设计进行了研究。国内不少学者也用过度自信理论来丰富委托代理模型，进行了初步的探究。严志辉等［12］将过度自信融入多任务委托代理模型，使传统的委托代理理论进一步拓展。黄健柏［13］认为要综合运用行为经济学、心理学中关于经营者的研究成果来研究经营者的非理性行为，以期提高激励契约效率。黄健柏等［14］以及陈其安等［15］通过委托代理模型对过度自信对努力程度，监督力度和激励等的影响进行了深入探讨。李娟等［16］对过度自信情形下委托人与代理人之间的薪酬合同进行了研究。

与笔者研究最接近的是文献［14］，它考虑了在次优合同情形下委托人和代理人非对称的过度自信水平对努力水平、激励系数的影响，并假设委托人和代理人对产出的平均水平拥有不同的信心，实际上过度自信可以表现为对随机变量的方差控制在较小的范围内，即kσ2。笔者假设委托人和代理人的不同过度自信源于对产出方差σ2的不同认知;同时，由于决策者在面对不确定性总是表现出一定的风险厌恶［17］，因此，笔者假设委托人和代理人都是风险厌恶的，并且进一步讨论了委托人和代理人同时努力时，非对称的过度自信水平对努力水平以及激励系数的影响。

2 基本假设与参数

考虑由一个委托人A和一个代理人B组成的两级供应链模型，为了便于分析，做如下假设:

假设1 委托人和代理人对产出的方差拥有不同的自信为kA和kB，即委托人认为产出方差为kAσ2，而代理人认为其为 kBσ2，两个人都认识到了这一不对称，并且委托人和代理人都没有根据他们的博弈更新他们的信心。

假设2 委托人支付给代理人的收益为π的线性函数，即 rB(π)=s0+bπ，其中 s0为固定报酬，b为收益分成系数(0≤b≤1)，此时，代理人的收益为rA(π)= －s0+(1－b)π。

假设4 委托人与代理人都遵从期望值决策准则，委托人和代理人都根据自己对收益期望值的判断进行决策选择。

笔者重新阐述文献［14］关于有利的自然状态和不利的自然状态的定义:

(1)当 kA，kB∈(0，1)时，kAσ2和 kBσ2分别为委托人和代理人对有利信号的认知，因为σ2是正常状态下的方差，所以小于σ2意味着有利的自然状态，kA，kB值越小表明对有利信号越过度自信。

(2)当kA，kB＞1 时，kAσ2和kBσ2分别为委托人和代理人对不利信号的认知，大于σ2意味着不利的自然状态。kA，kB值越大表明对不利信号越过度自信。

其他参数假设如下:w0为代理人的保留收益，ρA和 ρB(ρA，ρB＞0)为委托人和代理人的绝对风险规避常数，ξ为努力产出的随机干扰项，a和β分别为代理人和委托人的努力成本系数，V为委托人的效用函数，U为代理人的效用函数。为便于区分，用上角标s和d分别表示仅代理商努力以及委托人和代理人同时努力的两种情形。

3 仅代理人努力的委托代理模型

先讨论供应链的收益π仅为代理人努力水平esB的函数，即:

委托人和代理人进行的是Stackelberg博弈，事件发生的顺序如图1所示。首先委托人和代理人共同观察信号ξ，然后委托人给代理人提供固定报酬m0和分配系数bs，之后代理人选择努力水平esB，最后，委托人观察到不确定结果π。

根据委托代理理论，委托人和代理人的效用函数满足式(2):

图1 仅代理人努力的事件发生顺序

其中，E［V(rA(π)，bs)］为委托人的效用函数，约束条件分别表示代理人的参与约束和激励相容约束。

由于委托人和代理人都为风险规避性，收益风险会给委托人和代理人带来额外的风险成本，用Var(A)和Var(B)分别表示，则:

于是，委托人和代理人的效用函数的确定性等价收入可以表示为:

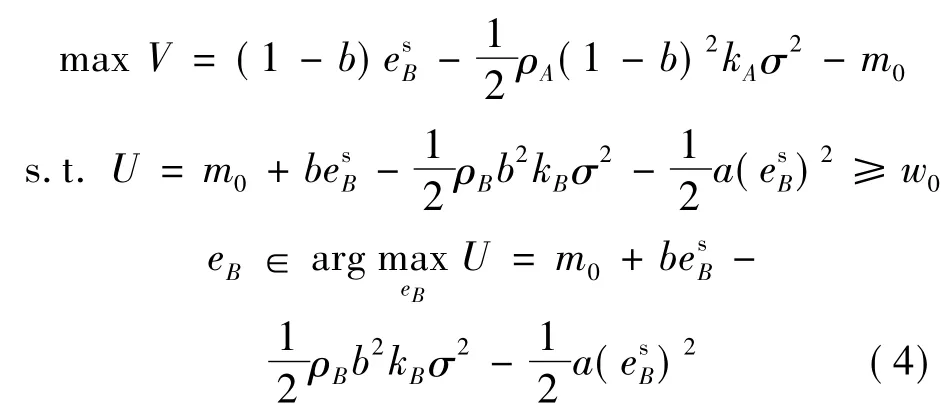
根据Stackelberg博弈的求解过程，对式(4)中代理人的效用函数U求esB的一阶偏导，并令其为0，可得:

在委托代理模型中，理性的委托人不会让代理人得到更多的收益，因此在最优条件下参与约束取等号，则式(4)可转化为:

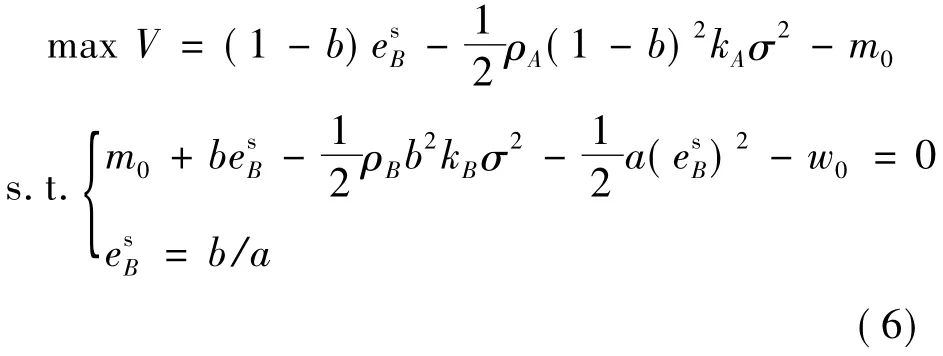
将约束条件代入目标函数，并对V求关于分配系数bs的一阶偏导，令其为0，可以得到:

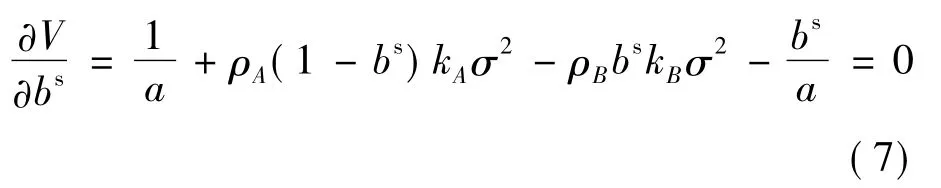
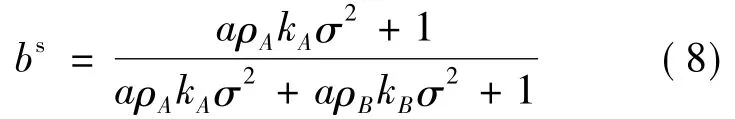
由此可以得到结论1:风险规避的委托人提供给风险规避的代理人的收入分配合同中分享系数努力水平为

对b和eB进行敏感性分析，可得到性质1:

(1)分配系数 bs满足∂bs/∂ρA＞0;∂bs/∂kA＞0;∂bs/∂ρB＜0;∂bs/∂kB＜0。

(2)努力水平 esB满足∂esB/∂ρA＞0;∂esB/∂kA＞0;∂esB/∂ρB＜0;∂esB/∂kB＜0。

证明 根据式(8)对分配系数b求ρA的一阶偏导，可以得到:

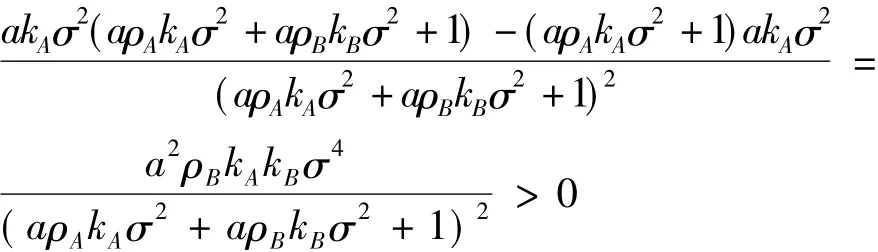
同理可证性质1的其他结论。

性质1表明委托人和代理人的风险规避态度ρA和ρB及其过度自信kA和kB都会影响最终合同的收入分享系数和代理人投入的努力水平。具体来说，当 kA，kB∈(0，1)，委托人对有利信号越过度自信，那么委托人愿意给予的激励系数越小，代理人愿意付出的努力越小，而代理人对有利信号越过度自信，代理人愿意接受的激励系数越高，代理人愿意投入的努力水平越高;当kA，kB＞1时，委托人对不利信号越自信，那么委托人愿意给予的激励系数越高，代理人愿意付出的努力越大，而代理人对不利信号越过度自信，代理人愿意接受的激励系数越低，代理人愿意投入的努力水平越小，这些与文献［14］的结论一致。

针对决策者不同的风险态度，委托人的风险规避系数越大，则委托人愿意给予的激励系数越高，代理人愿意投入的努力水平越大;特别地，考虑文献［14］中委托人是风险中性，即ρB=0时，则有，也就是说风险规避性的委托人比风险中性的委托人愿意提供更高的收入分配系数，当然，此时委托人承担的风险会降低，即σ2A=(1－bs)2kAσ2减小。

代理人的风险规避系数越大，则委托人愿意给予的激励系数越低，代理人愿意投入的努力水平越小，特别地，若代理人是绝对风险规避性，即ρB→∞，那么bs=0，此时，代理人仅愿意接受固定支付，并且消极怠工。

4 委托人和代理人都努力的委托代理模型

笔者进一步讨论委托人和代理人同时付出努力时，风险态度和过度自信水平对分配系数以及努力水平的影响。

假设供应链的收益π是委托人和代理人努力水平edA和edB的线性函数，即:

其中，θ为委托人的努力水平对收益的贡献系数(相对于代理人来说)，θ＞1为委托人的努力对于供应链收益的贡献大于代理人，θ＜1为委托人的努力对于供应链收益的贡献不如代理人，θ=1为两人的贡献一样。

委托人和代理人Stackelberg博弈顺序如图2所示。首先委托人和代理人共同观察信号ξ，然后委托人给代理人提供固定报酬m0和分配系数bd，并确定努力水平edA，之后代理人选择努力水平edB，最后，委托人观察到不确定结果π。

图2 委托人和代理人同时努力的事件发生顺序

其中，目标函数表示委托人的效用函数，约束条件分别表示代理人的参与约束和激励相容约束。对式(10)中代理人的效用函数U求edB的一阶偏导，并令其为0，可得:

在委托代理模型中，理性的委托人不会让代理人得到更多的收益，因此在最优条件下参与约束取等号，则模型式(10)可转化为:

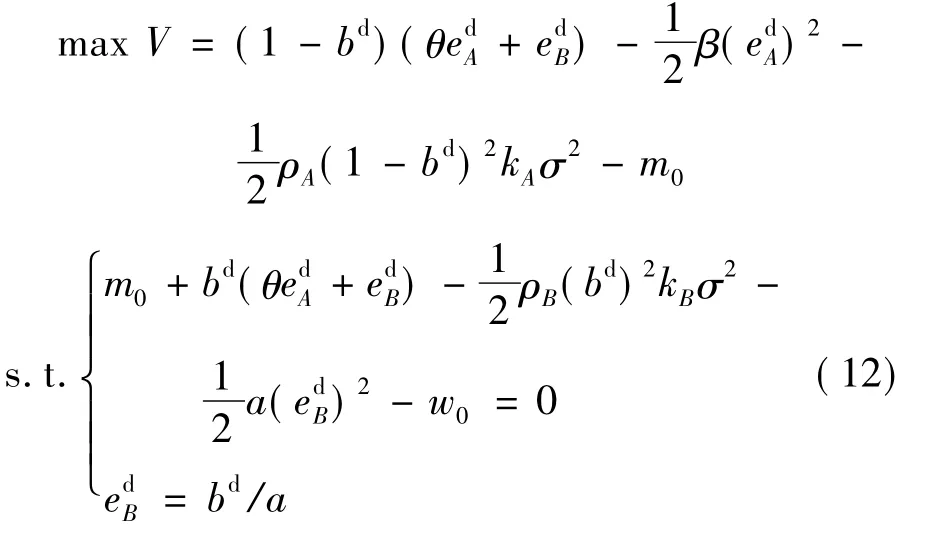
将约束条件代入目标函数，并对V求关于努力水平edA和分配系数bd的一阶偏导，令其为0，可得:

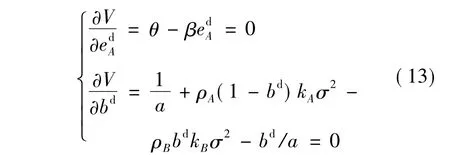
而V的海塞矩阵为:

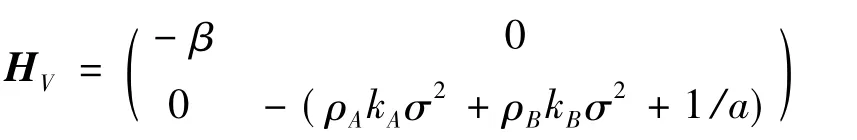
容易判断HV为负定矩阵，那么V是关于ed和bd的凹函数，即一阶条件式(13)为委托人的效用函数取最大值的条件，经化简可以得到委托人最优的分配系数和投入的努力水平为:

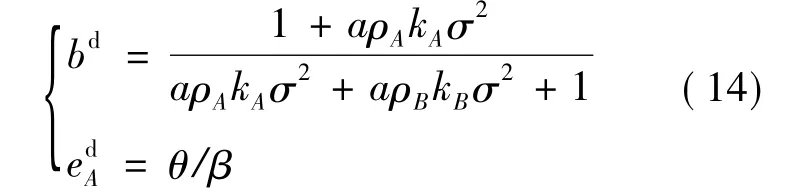
值得注意的是，委托人投入的努力水平只与其收入贡献系数和努力成本系数相关，与委托人愿意提供的分配系数和代理人的努力成本系数无关，由此可以得到结论2。

结论2:风险规避性的委托人提供给风险规避性的代理人的收入分配合同中分享系数，努力水平分别为和

对比结论1和结论2，可以发现，仅代理人努力、委托人和代理人同时努力，以及代理人投入努力程度的分配系数表达式相同，由此可得结论3。

结论3:委托人是否投入努力不影响最终的收入分配系数，也不影响代理人努力水平的选择。

结论3表明委托人投入的努力并不能增加其在合同谈判中的砝码，但这并不代表委托人没有动机付出努力，对于委托人来说，增加单位的努力水平获得的收益大于产生的成本，委托人就有利润动机付出努力。

通过对edA和bd进行敏感性分析，同样可以得到类似于性质1的结果:

(1)分配系数 bd满足∂bd/∂ρA＞0;∂bd/∂kA＞0;∂bd/∂ρB＜0;∂bd/∂kB＜0。

(2)委托人的努力水平 edA与 ρA、kA、ρB和 kB无关。

(3)代理人的努力水平 edB满足∂edB/∂ρA＞0;∂edB/∂kA＞0;∂edB/∂ρB＜0;∂edB/∂kB＜0。

5 结论

考虑当决策者对努力产出的方差拥有不同自信时，讨论了风险态度和过度自信水平对最终努力水平和收入分配系数的影响机制，并分别针对仅代理人努力以及委托人和代理人同时努力两种情形进行研究，结果发现，委托人和代理人对努力产出分布方差的不同过度自信和各自的风险态度会对收入分配系数和代理人的努力水平产生影响，谁能优先获取对市场状态更有利的信息，谁就能在合同谈判中占据更加有利的地位，而抗风险能力的大小也同样决定其在合同制定中的话语权。对委托人来说，当委托人和代理人拥有不同的过度自信水平，对收益风险敏感程度不同时，委托人应根据双方过度自信水平和风险态度适当调整薪酬契约，使委托代理双方获得相对满意的结果。有趣的是，委托人在选择投入的努力水平并不受过度自信水平和风险态度的影响，这与委托人在合同谈判中占据主导地位不无关系。假设产出是努力的线性函数，在实际经济活动中，通过构建销售渠道和电子信息平台等投入获取更正确的市场信息，即努力水平产生会影响产出方差，且当两人同时努力发生1+1＞2的情况，是否可以得

A到最优解仍需进一步探究。

［1］WEINSTEIN N D.Unrealistic optimism about future life events［J］.Journal of Personality and Social Psychology，1980，39(5):806 －820.

［2］HILARY G，MENZLY L.Does past success lead analysts to become overconfident? ［J］.Management Science，2006，52(4):489 －500.

［3］BERNARDOA E，WELCH I.On the evolution of overconfidence and entrepreneurs［J］.Journal of Economics＆ Management Strategy，2001，10(3):301－330.

［4］MALMENDIER U，TATEG.CEO overconfidence and corporate investment［J］.The Journal of Finance，2005，60(6):2661 －2700.

［5］BUSENITZ LW，BARNEY J B.Differences between entrepreneurs and managers in large organizations:biases and heuristics in strategic decision － making［J］.Journal of Business Venturing，1997，12(1):9 －30.

［6］GERVARISS，HEATON JB，ODEAN T.The positive role of overconfidence and optimism in investment policy［R］.Philadelphia:University of Pennsylvania，2002.

［7］GERVARIS S，HEATON J B，ODEAN T.Overconfidence，compensation contracts，and capital budgeting［J］.The Journal of Finance，2011，66(5):1735 －1777.

［8］SCHRAND C M，ZECHMAN S L C.Executive overconfidence and the slippery slope to financial misreporting［J］.Journal of Accounting and Economics，2012，53(1):311 －329.

［9］BOLTON P，SCHEINKMAN J，XIONGW.Executive compensation and short－termistbehaviour in speculativemarkets［J］.The Review of Economic Studies，2006，73(3):577 －610.

［10］KEIBER K L.Managerial compensation contracts and overconfidence［R］.Berlin:WHU Otto Beisheim Graduate School of Management，2002.

［11］ROSA L E.Overconfidence and moral hazard［J］.Games and Economic Behavior，2011，73(2):429－451.

［12］严志辉，钟美瑞，黄健柏.基于过度自信的多任务委托:代理模型扩展研究［J］.系统工程，2006(2):19－22.

［13］黄健柏.我国经理人市场激励契约设计与效率研究［D］.长沙:中南大学图书馆，2004.

［14］黄健柏，杨涛，伍如昕.非对称过度自信条件下委托代理模型［J］.系统工程理论与实践，2009，29(4):92－102.

［15］陈其安，杨秀苔.基于代理人过度自信的委托－代理关系模型研究［J］.管理工程学报，2007(1):110－116.

［16］李娟，郝忠原，陈彩华.过度自信委托代理人间的薪酬合同研究［J］.系统工程理论与实践，2013，33(1):1－9.

［17］罗春林，黄健，柳键.不同风险偏好下的供应链定价与订货策略［J］.计算机集成制造系统，2012(4):859－866.