基于Ansoft的永磁悬浮直线导轨平台的设计及磁力分析

张海龙，张坚，孟庆涛，邹文，张钢

(上海大学 机电工程与自动化学院，上海 200072)

永磁悬浮支承技术是磁悬浮支承技术的一种，根据Earnshaw定律[1]，只用永磁悬浮支承无法实现稳定的全永磁悬浮，因此需要同时采用辅助支承。所用的辅助支承不同，永磁悬浮机构的特点也不同。相比主动磁悬浮技术，永磁悬浮技术具有结构简单、成本低、无需电控系统、结构尺寸小和无需润滑密封等优点。而相比常规的滚动与滑动轴承，它具有微摩擦和寿命长等优点，成本甚至接近于滚动支承，具有很大的发展前景[2-5]。

目前，对永磁悬浮轴承的研究较多[2-8]，而对永磁悬浮导轨的研究却很少。在此提出了2种永磁悬浮支承的直线导轨平台方案，拟用在航母所用的电磁弹射器上。对这2种方案进行了详细说明和承载能力及刚度的计算，并对比了2种方案各自的优缺点和适用场合。这种永磁悬浮直线导轨平台除了可应用在电磁弹射器上，也可以用在其他需要直线运动的场合，如机床导轨等。

1 设计方案

弹射器是航母的重要部件，对航母的战斗力具有重要的影响。目前，最为先进的是美国用于下一代福特号航母上的电磁弹射器，采用了“大功率直线电动机驱动技术+飞机轮子支承”方案，文中驱动技术借鉴美国方案，也采取大功率直线电动机驱动方案，但支承改为磁悬浮支承技术。由于本方案支承方式与美国方案不同，研究对象是永磁悬浮导轨支承平台，所以体积、重量比美国的均大大缩小且不成比例。所提出的“大功率直线电动机驱动技术+永磁悬浮导轨支承平台”方案若能成功使用将会改进电磁弹射器的性能。

方案如图1所示，其中左侧是没有采用磁悬浮支承技术的美国方案，右侧是采用永磁悬浮导轨支承的方案。

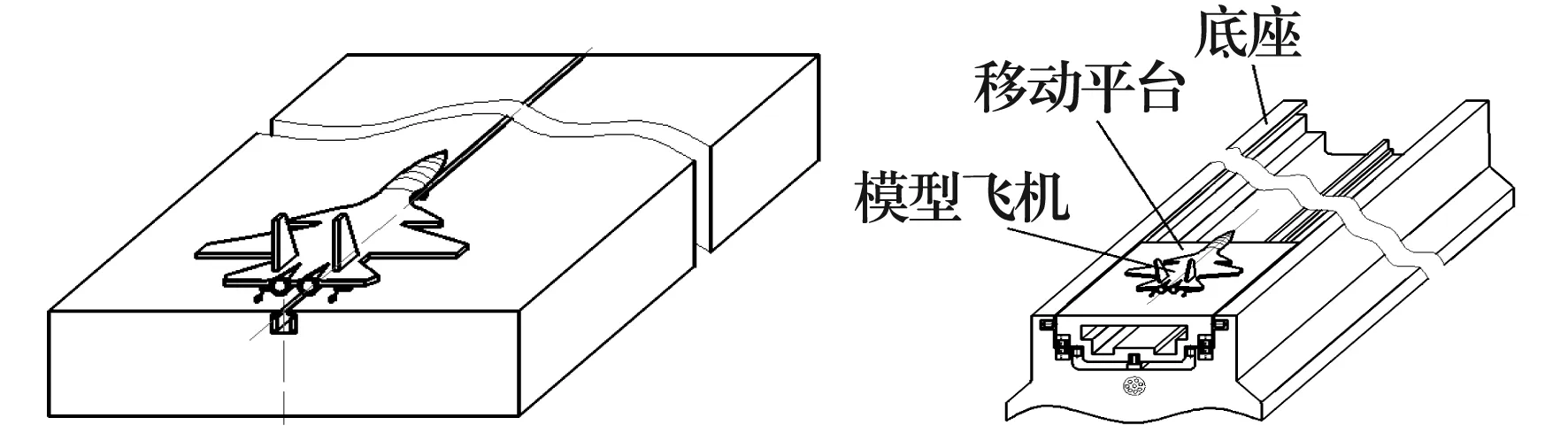
图1 磁悬浮支承的电磁弹射器方案

1.1 4磁条方案

4磁条方案的原理及平台受力情况如图2所示。

图2 4磁条永磁导轨的截面图

此方案中，平台和底座上各装有2根磁条，磁条充磁方向为竖直方向。磁条间的初始气隙为5 mm。底座上的2条条形磁铁与平台上的2条磁铁磁极相反从而产生承载的斥力。另外下部还安装有直线电动机和2组滚轮。其中一组滚轮为侧向辅助支承，另一组为竖直方向上的辅助支承。Fz1与Fz2为平台所受磁斥力，Fz3与Fz4为滚轮所受的力，F为平台的自重与外载荷(包括直线电动机竖直方向很小的分力)的合力。假设平台稳定，则有

Fz1+Fz2=F+Fz3+Fz4。

(1)

当F较小时，磁力Fz1+Fz2为初始气隙5 mm时的磁力，此时滚轮和平台底座接触受力，平台在垂直方向没有完全悬浮。当F较大时，5 mm气隙所产生的磁力Fz1+Fz2不足以承载，平台会下降，此时，竖直方向起辅助支承作用的滚轮会与底座上的面分离，滚轮不再起支承作用，由此可得

Fz3+Fz4=0，

(2)

此时平台在垂直方向为完全磁悬浮支承，摩擦阻力最小。平台下降时，随着平台下降距离Δz的减小，磁力Fz1+Fz2会变大，到某一位置时平台会重新平衡。此时有

F=Fz1+Fz2。

(3)

1.2 8磁条方案

8磁条方案的受力情况如图3所示。

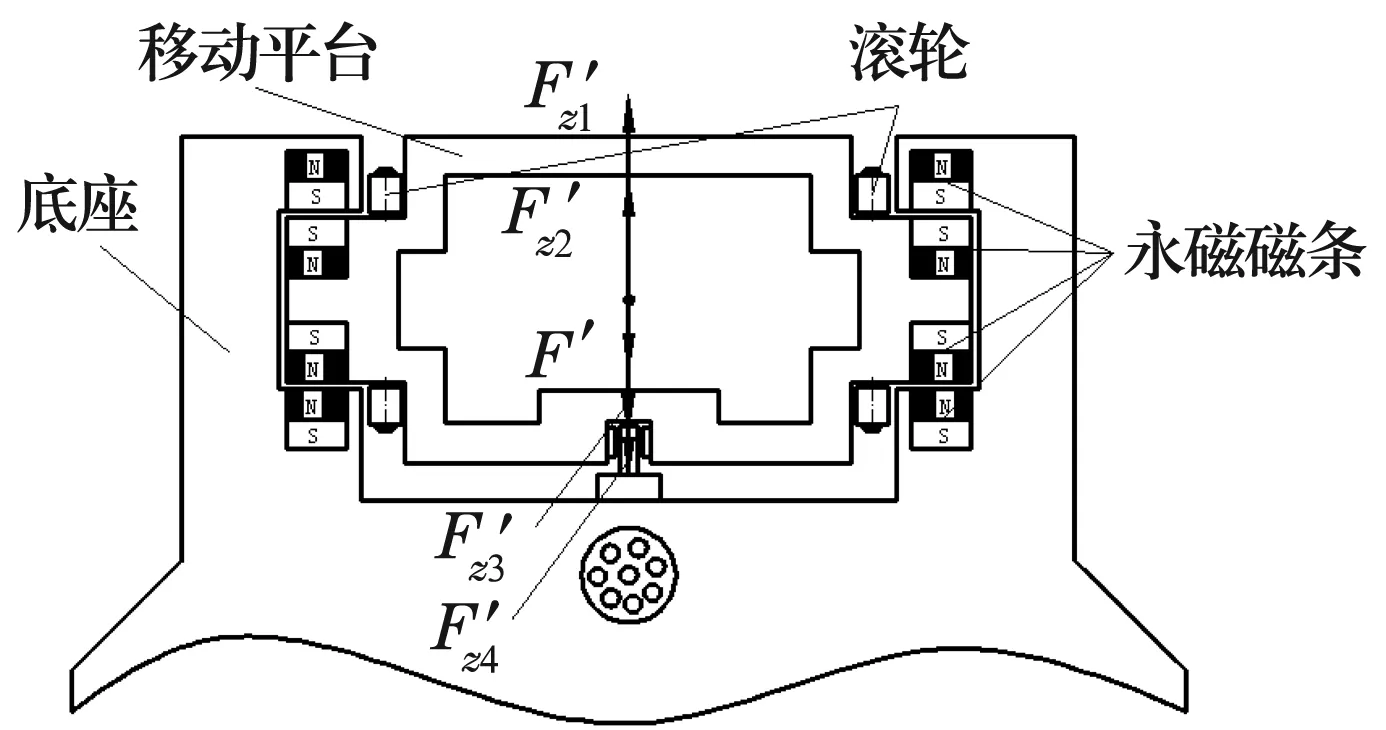
图3 8磁条永磁导轨的截面图

(4)

当平台处于中间位置时，上下气隙相等，则有

(5)

(6)

1.3 方案对比

对比2种方案可得：

(1)4磁条方案只有在一定外载荷下，平台在垂直方向才能完全悬浮；而8磁条方案在没有外载荷时，平台在垂直方向也可以完全悬浮。

(2)在同样的结构参数和气隙条件下，4磁条方案节省磁性材料，占用空间小，且承载力大。

由以上分析可以看出，2种方案各有优缺点，适用于不同的场合。

2 力学分析

2.1 磁场和磁力分析理论基础

选用电磁场有限元分析软件Ansoft Maxwell v14.0进行磁力磁场的计算。Maxwell是电磁场有限元分析最常用的软件之一，基于Maxwell电磁场方程组进行计算分析，不仅功能强大，也可以很好地控制计算精度。在网格划分时，除了可以采用有限元网格自适应划分技术，也可以手动划分。软件提供了多种网格参数控制方法，可以有效地控制网格的大小，这对计算精度非常重要。

对于静磁场的磁力，需要求磁场分布，然后在此基础上求磁力和力矩。Maxwell的静磁场求解器根据安培定律和高斯磁通定律计算

(7)

(8)

计算磁力和力矩采用虚位移法，永磁体磁力的计算公式为[9]

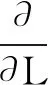
(9)

(10)

式中：L为运动方向的位移；Wm为磁场能量；B为磁通密度；H为磁场强度；V为被求磁力物体的体积。

三维静磁场的边界条件可以直接采用系统默认：物体间交界面的边界条件为自然边界条件，即跨越物体之间界面磁场强度H的切向分量和磁感应强度B的法向分量是连续的，并且满足[9]

Ht1=Ht2+Js,

(11)

Bn1=Bn2,

(12)

式中：Ht为分界面处磁场强度的切向分量；Bn为分界面处磁通密度的法向分量；Js为表面电流密度。

外边界条件为诺依曼边界条件：磁场H与表面边界相切，强制磁场强度的法向分量为0。

虚功法计算精度高[10]，而Ansoft中又可以控制迭代精度，从而可以保证计算的准确性。

2.2 承载能力和刚度的分析

永磁体磁条材料采用各向异性的烧结钕铁硼，充磁方向上的矫顽力Hc=907 000 A/m，相对磁导率μr=1.067，剩余磁通Br=1.21 T。平台上的短磁条尺寸为40 mm×40 mm×400 mm，底座上的长磁条尺寸为40 mm×40 mm×2 000 mm，磁条之间的初始气隙取c=5 mm。计算时平台处于中间位置。

利用Ansoft进行建模及计算：网格划分设置磁条细化；求解区域设为200%；迭代计算误差1%，最大迭代次数20次；单元加密比例为30%；边界条件采用系统默认；选择平台上的所有磁条计算其受力，所得力即为平台所受的磁力之和。建模时不考虑除磁条之外的其他结构对磁场和磁力的影响，这是因为这些结构采用铝合金或陶瓷等材料，对磁场基本无影响。计算过程中发现划分的四面体单元个数为142 755～151 285，迭代8～10次即可满足1%的收敛要求。网格划分情况如图4所示，由图可知网格很密，比较理想。用主流配置的计算机完成一次计算需要10 min左右。

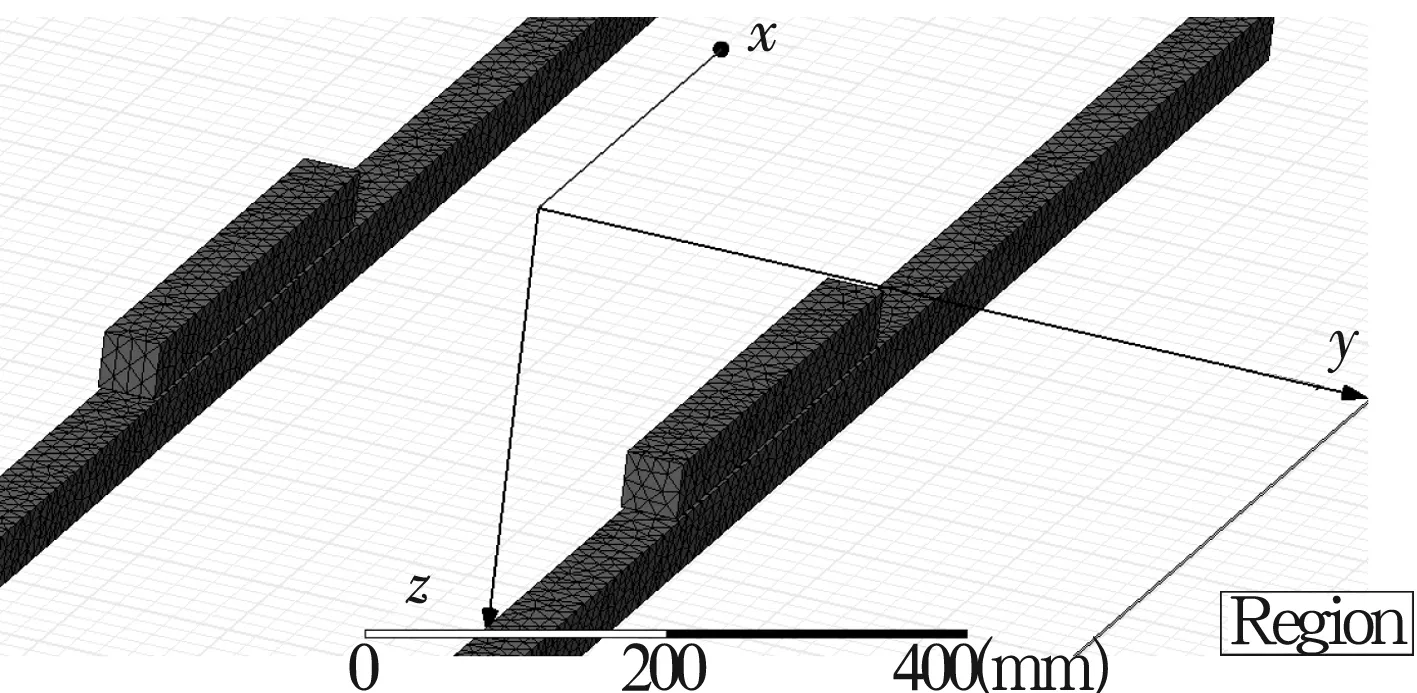
图4 磁条网格划分

计算的其他必要参数及所用的右手坐标系如图5所示。模拟时，采用1∶50的比例进行缩小。

图5 坐标系和计算参数

2种方案的初始气隙均为5 mm，以0.5 mm的气隙间隔来计算平台在不同气隙条件下的磁力变化。令竖直方向上的磁力Fz为承载力，Δz为平台在z方向的偏移距离，通过计算2组模型的平台在不同偏移量Δz时的磁力可以得出2组数据结果如图6所示。对于4磁条方案和8磁条方案的另外2个方向上的磁力Fy和Fx，所有数据的绝对值均小于5 N，说明这2个方向存在较小的不稳定力，需要辅助轮和直线电动机来承受。

图6 2种方案的磁力计算比较

根据最小二乘拟合曲线的公式

(13)

(14)

可以求得2种模型磁力曲线拟合所对应的一次函数方程

y=Ax+B。

(15)

计算可得4磁条方案的一次函数拟合方程为

Fz=519.01Δz+6 542.93，

(16)

同样可得8磁条方案的一次函数拟合方程为

(17)

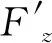
从承载角度分析：

(1)若采用4磁条方案，平台偏移Δz=0时，最大承载力为6 642 N；Δz=4 mm时，最大承载力为8 652 N。但这种方案要求承载力必须大于6 643 N时,平台在垂直方向才可以完全磁悬浮。

(2)若采用8磁条方案，平台偏移Δz=0时，承载力为0；Δz=4 mm时，承载力为3 470 N。

对比以上结果可以发现，采用同样尺寸的磁条，尽管8磁条方案耗用2倍的磁性材料，结构也增大了，但承载能力却不足4磁条方案的一半。反之，若要8磁条方案拥有同样的承载力，需要耗费更多的永磁材料和占用更多的空间。虽然4磁条方案在垂直方向完全悬浮有一定的约束条件，但这可以根据实际工况通过合理的参数设计来克服。

综上所述，4磁条方案适用于重载低刚度工况，8磁条方案适用于轻载高刚度工况。

2.3 平台不同位置时的磁力变化

考虑到长磁条两端的磁场分布与中间的磁场分布有所不同，因此有必要对比平台在两端位置的磁力和中间位置的磁力变化。为了观察平台从一端运动到另外一端时磁力的变化规律，每隔一段距离计算一次，从而得出磁力-位置曲线图。根据模型的对称性，可以只分析平台从中间到一端的磁力变化。计算时采用4磁条模型和气隙c=5 mm的基本参数。

首先以100 mm为间隔，当平台处于边缘位置时，令位移s=0，当平台运动到中间时，根据底座上磁条的长度(2 000 mm)及平台的长度(400 mm)可得s=800 mm，一共需要计算9组数据。同样利用Ansoft进行计算，计算基本设置参考前文，此次网格划分的四面体单元个数在146 319～155 631之间，网格划分情况和图4类似，通过迭代8次即可满足计算精度要求，所得数据见表1。

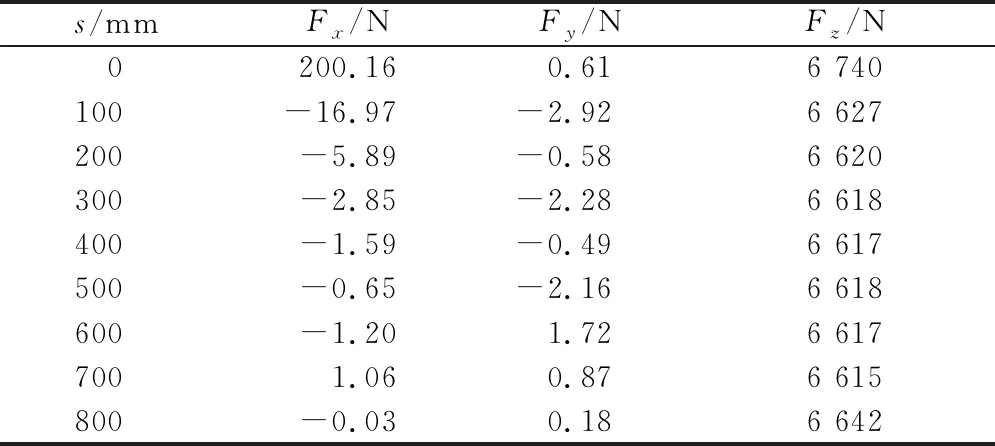
表1 4磁条模型磁力与位置关系

分析以上数据可知，不同位置Fy的绝对值都很小，这是由软件计算误差产生的，理论上应该为0，也说明该方向受力不太平衡，必须采用辅助轮进行定位(由辅助轮承受的力比较小)。Fz随位置的改变也无显著变化。Fx在s=0时有较大的磁力，数值为Fz的3%；随着平台往中间移动Fx逐渐变小，s=100 mm之后Fx变得很小。

为了研究Fx的详细变化，在s=0～200 mm区间内以10 mm为间隔继续分析磁力。根据所得数据绘制曲线图如图7所示，由图可知，磁力在x轴方向的分量Fx主要出现在s=30 mm之前，在s=0～30 mm区间内Fx快速下降，约在50 mm处逐渐趋于0。Fx最大值出现在s=0处，为200.16 N，方向为x轴正向，这是由于边缘不对称效应引起的，不可忽略。x轴方向是直线电动机驱动的方向，因此，设计选用直线电动机时需要考虑这一外力的影响。

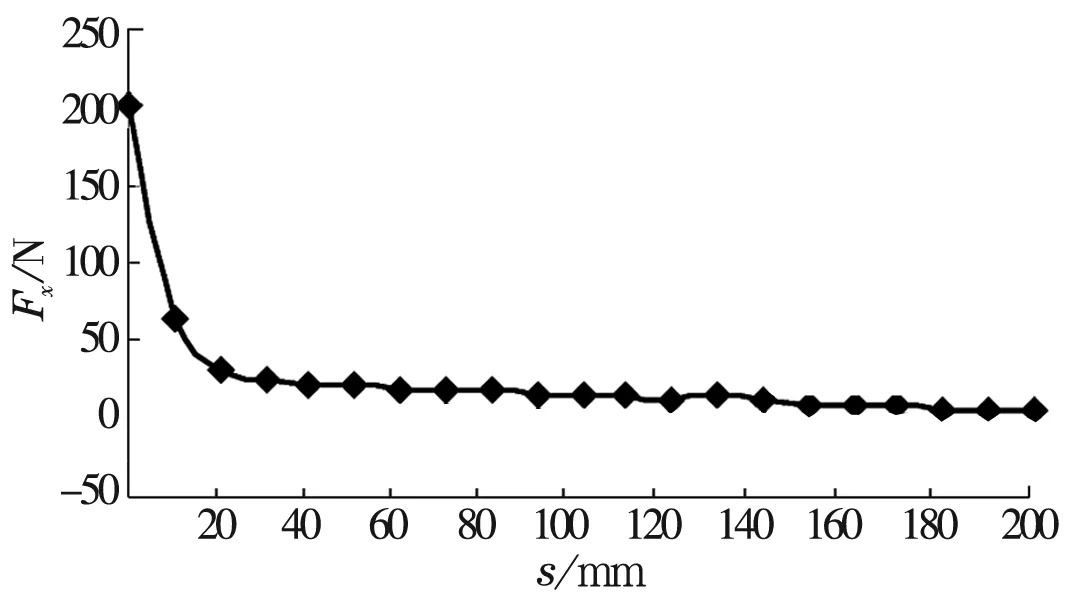
图7 4磁条模型磁力-位置关系图

继续分析s=0～10 mm时Fx的变化，以1 mm为间隔，得到如图8所示的曲线图。这一阶段Fx呈近似直线下降趋势，此结果可以作为直线电动机设计计算的依据。

图8 s=0～10 mm时Fx的变化

3 结论

利用Ansoft Maxwell对2种方案进行了磁力计算，并对4磁条模型平台不同位置时的磁力变化做了计算分析，得出以下结论：

(1)相比8磁条方案，4磁条方案具有耗用磁性材料少、结构紧凑、承载能力大等优点，也有刚度较小和完全悬浮的约束条件，但这些缺点可通过合理的参数设计来克服。说明4磁条方案适用于重载低刚度场合，8磁条方案适用于轻载高刚度场合。

(2)随着永磁悬浮支承移动平台位置的变化，竖直方向或承载方向上的磁力Fz基本无变化，但沿运动方向上的磁力Fx却有明显变化，这是由于磁条边缘处的磁场和磁条中间的磁场不同而引起的，这一特点将对直线电动机的设计产生一定影响。