ART2神经网络的一种改进
陈国灿,高茂庭
上海海事大学信息工程学院,上海 201306
ART2神经网络的一种改进
陈国灿,高茂庭
上海海事大学信息工程学院,上海 201306
1 引言
自适应共振理论(Adaptive Resonance Theory,ART)神经网络是一种自组织、无监督学习神经网络[1-3],具有能够迅速自组织地进行对输入模式的识别并聚类,并且能够把陷入在各种噪声背景里的近似信号挑出来并进行加强等优点[2,4]。
但传统的ART2神经网络[2,5]在对输入模式进行识别聚类时,由于只利用了输入模式的相位信息,而忽视了其幅度信息的作用[6-7],在处理相位相同而幅度不同的输入模式簇时,难以将它们区分开,聚类效果不理想;同时,它还对输入模式中各神经元取值存在着一定的限制,在F1层中将输入模式中非正实数统一作为0处理,导致输入模式的部分信息丢失,影响了聚类结果。
本文对传统的ART2网络从几个方面进行改进,一方面,在输入模式进入网络学习的同时,既考虑它的相位信息,同时也计算其到各个簇的中心点的最短距离,综合考虑其幅度信息;另一方面,还对非线性变换函数(滤噪)做了相应的处理,使其能正确地处理负数的输入,并在F1层稳定后仍保持其负数形式,不会导致输入模式的信息丢失;再一方面,为了消除离群点对聚类结果的影响,本文还对输入模式进行了离群点的判定。最后,通过实验验证了这种改进方法的可行性和有效性。
2 传统的ART2神经网络
2.1 ART2神经网络的结构
ART2神经网络的基本思想是竞争学习机制和自稳学习机制[2],ART2神经网络为两层结构[5,8],分别为F1层和F2层,其中F1层有n个输入节点,F2层有m个输出节点。网络的两层之间既存在从F1层到F2层的前馈连接权wij(i=1,2,…,n;j=1,2,…,m),也存在从F2层到F1层的反馈连接权tij(i=1,2,…,n;j=1,2,…,m),此外,网络还包含一个复位信号R来实现F2层的重置。ART2神经网络中单个神经元的典型结构如图1所示。
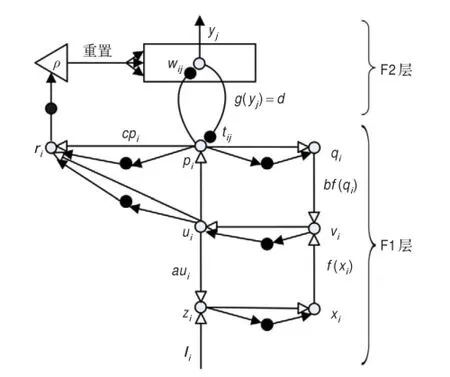
图1 ART2神经网络中单个神经元结构图
ART2神经网络也可以分成注意子系统和取向子系统。注意子系统完成自下向上矢量的竞争选择及矢量间相似度的比较,取向子系统检查相似度能否达到满意的标准,并作出相应的动作。
2.2 ART2神经网络学习算法

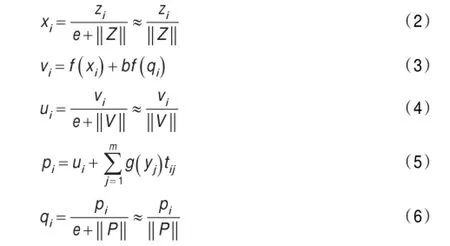
其中公式(3)中函数f(x)是非线性处理函数,用于对传送的信号进行非线性变换,归一化处理和非线性处理的结合确定了噪声判定标准,并使网络能够从噪声中分离出信号,非线性处理函数f(x)的非线性程度决定了对比增强和噪声抑制的程度,函数f(x)定义为:
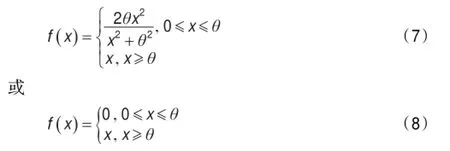

F2层选择出获胜神经元j并送回一个反馈信号,然后计算STM变量P和U的匹配度‖‖R,也就是F1层中经过处理的STM信号与激活的LTM(Long Time Memory)信号之间的匹配度,计算公式如下:
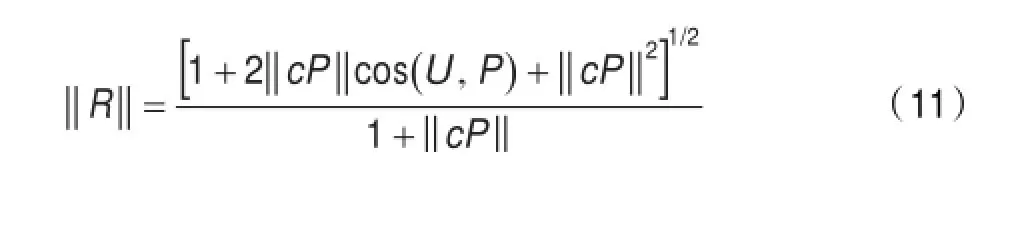
当‖R‖大于规定的警戒值ρ时,LTM信号进入学习阶段,即

反之,取向子系统发出重置信号,F2层神经元重新竞争,相似度第二大的神经元获胜。
3 一种改进的ART2神经网络
传统的ART2神经网络是按相位信息聚类的,与幅值信息无关[9-15]。传统的ART2神经网络在处理相同相位信息而幅值信息不同的两个簇时,效果很不理想。一些文章中也提到了通过比较权值和输入样本的模来恢复幅度信息[7],但这种权值并不能反映模式原型的幅度信息,所以仍然无法利用幅度信息。
对原始数据有正有负的数据样本,由于传统的ART2网络存在输入域的限制[13],传统的ART2网络的F1层中将样本数据的非正实数抑制为0,因此传统的ART2网络不能将位于第二、三、四象限的数据样本进行有效地分类。
同时,传统的ART2神经网络对离群点的存在不敏感,为了尽量消除离群点对聚类结果的影响,本文改进算法通过将离群点另外作为一类,以减小离群点对聚类结果的影响。
针对传统ART2神经网络存在的上述不足之处,本文通过在输入激活过程中,计算其到各个簇的中心点的最短距离,综合考虑其幅度信息,若相位和幅度两者均超过相应的警戒阈值时,才发生谐振并调整权值;对非线性变换函数(滤噪),也做了相应的处理,使其能正确地处理负数的输入,并在F1层稳定后仍保持其负数形式,以免导致输入模式的信息丢失;为了消除离群点对聚类结果的影响,本文还对输入模式进行了离群点的判定,并增加一个阈值R_dis来检测离群点。改进的ART2神经网络相位与幅度匹配如图2所示。
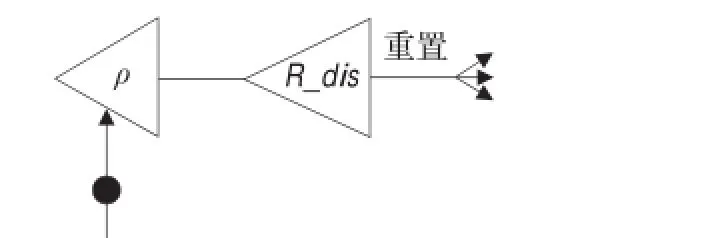
图2 改进的ART2神经网络中相位与幅度匹配
该方法的主要思想是:在数据样本进入F1层,经过F1层的自稳学习后,幅度信息原型Ii通过进行竞争学习找出获胜神经元,与其距离最短的神经元获胜。获胜神经元自上向下反馈一个信号强度,反馈的信息P=(p1,p2,…,pn)与F1层中稳定的输入模式的相位信息U=(u1,u2,…,un)进行相位匹配度计算以及离群点检测,若两者有一个不符合所设定的阈值要求,则重新开辟一个簇,否则将输入模式归入获胜神经元所在的簇。改进的ART2神经网络算法流程如图3所示。
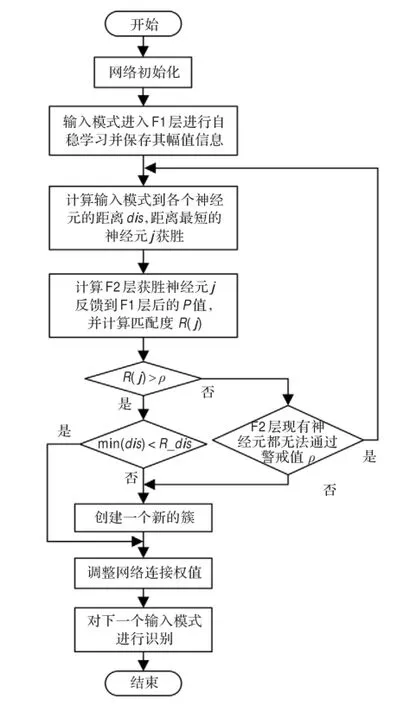
图3 改进的ART2算法流程图
改进后的ART2网络也包含注意子系统和取向子系统。注意子系统包括F1和F2两个短期存储单元STM以及连接F1和F2层的长期存储单元LTM即连接权向量Wn×m和Tn×m,此时自下向上的连接权向量wij记录的是簇的中心点幅度信息,其中第j列表示第j类的中心点。取向子系统的作用是计算输入模式与记忆模式间相位匹配程度,即F1层稳定的中间模式U与获胜神经元自上向下的反馈模式P进行相位匹配,以及对输入模式进行离群点检测,以此来决定网络接下来的动作:共振或重置。
首先,对网络进行初始化设置。改进的ART2网络中F1层的初始化以及自上向下的权向量Tn×m的初始化和传统的ART2网络相同。簇的个数m设置为1,自下向上的连接权向量Wn×m初始化第一个输入模式作为第一个簇的中心点,即同时还需要设定两个阈值ρ和R_dis,ρ作为相位匹配度的警戒值,R_dis作为离群点判定的警戒值。
当n维输入模式I=(I1,I2,…,In)进入F1层后,通过公式(1)~(6)计算F1层的稳定状态,由于传统的ART2网络将非正实数统一作为0处理,非线性转换函数将其作为噪声处理,使得网络丢失了该部分的信息,影响了整个聚类结果。因此需要调整非线性处理函数以便能正确地处理非正实数,防止将有用的信息误作为噪声处理。非线性处理函数调整为:
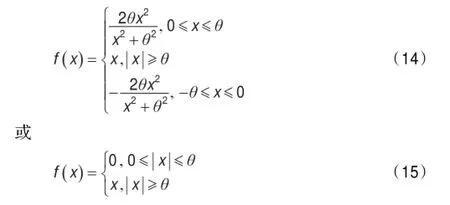
F1层达到稳定状态后,输入模式I经过自下向上的连接权向量Wn×m传入F2层并进行竞争学习,找到与其距离最短的神经元作为获胜神经元,即获胜神经元被激活,其他神经元则处于抑制状态,F2层选择出获胜神经元j并送回一个反馈信号,并计算F1层中经过处理的STM信号U与激活神经元的LTM信号的反馈值P之间的相位匹配度‖‖R。由于‖‖R反映的是P和U的整体匹配程度,而不管P和U的各分量之间的差异,在这里本文仍采用公式(11)进行相位匹配计算。若匹配度‖‖R大于所设定的阈值ρ,则对输入模式进行离群点判定,即若kj大于预先设定的阈值R_dis,则将该输入模式作为离群点处理,将该输入模式作为单独的一个类,将输入模式划入第j类中,网络进入学习阶段,自下向上的权向量wij更新为第j类的新的中心点即第j类所有数据样本的各分量的均值,自上向下的权向量tij按公式(13)进行更新。
对于传统ART2网络,当输入模式进入F1层后,进行共振直到F1层处于稳定状态,由于输入模式进入F1层时,F2层无反馈信息进入,实际上只需要1~2次共振使得F1层处于稳定状态,再进入F2层,计算与F2层m个神经元的相似度,最大相似度神经元获胜,获胜神经元反馈一个信号,并进行匹配计算,如果匹配度小于预先设定的阈值则F2层重置,寻找次胜神经元,最坏情况下F2层重置次数为m次,否则网络进入学习阶段,因此,算法时间复杂度O(mn),其中,n为输入模式的个数;改进的ART2网络在F1层仍只需要进行1~2次共振就能达到稳定状态,F1层稳定后输入模式传递至F2层,计算出与m个神经元的距离,距离最短的神经元获胜,获胜神经元反馈一个信号,并进行匹配计算,如果匹配度小于预先设定的阈值则F2层重置,寻找次胜神经元,最坏情况下F2层重置次数为m次,否则网络进行一次离群点判定,改进算法F2层的判定次数要比传统的ART2的判定次数多一次,即F2层重置次数的最坏情况为m+1次,故改进算法的时间复杂度仍为O(mn)。虽然改进算法的复杂度在数量级上无变化,但在处理相同相位不可分的情况下的准确率要比传统ART2网络有明显提高。
4 实验和结果分析
本文利用上述算法针对横、纵坐标在[0,1]的范围内随机生成的5个特征明显的类,每类包含30个数据样本进行聚类。分别用传统的ART2与改进后的ART2网络对该数据样本进行聚类,聚类结果分别如图4和图5所示,其中各个参数设置如表1所示,其中参数a、b、c、d、e的取值均参照文献[2]中的参数设置,这些参数还可通过实验经验来取值。
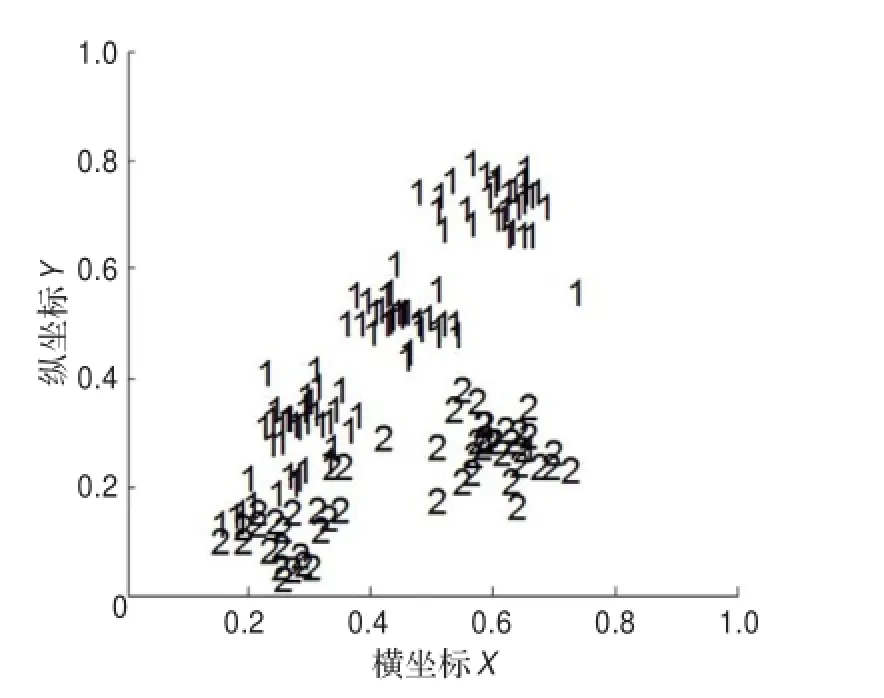
图4 传统ART2网络聚类结果
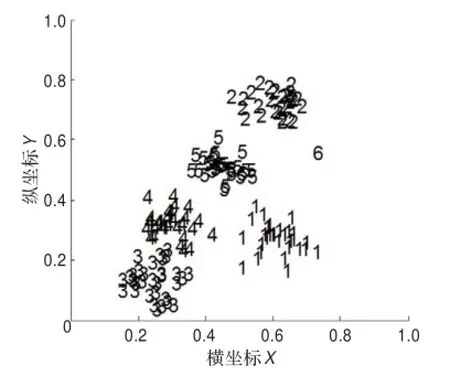
图5 改进后ART2网络聚类结果
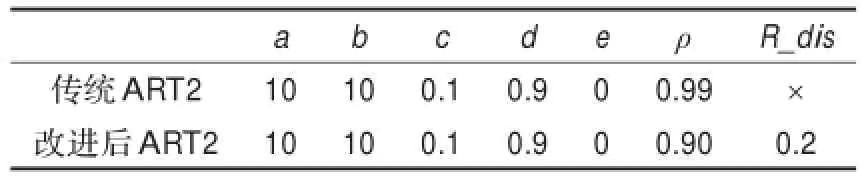
表1 网络参数设置表
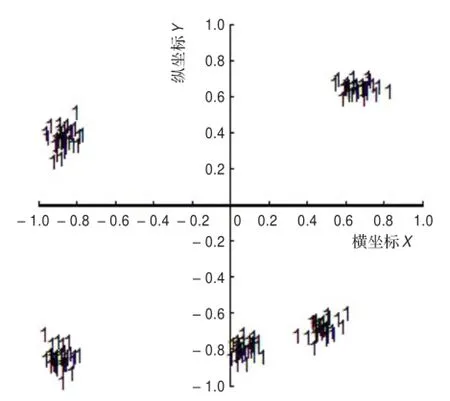
图6 传统ART2的四个象限内数据聚类

图7 改进后四个象限内数据样本的聚类
传统的ART2网络在数据处理过程中将样本数据进行归一化处理,只保留了数据的相位信息,相位信息通过竞争学习进行聚类后,得到的聚类结果只考虑了数据样本的相位信息而忽略了数据的幅度信息,将相位信息相同或相近的样本数据划分在同一个类中。由图4可以看出,相位相同或相近的数据样本被划分在同一个类中,无法将相位相同或相近的两个类区分开来。改进后的ART2网络,在数据处理的过程中不仅将数据进行归一化处理,同时还保留了数据原型的幅度信息。在竞争学习时,通过将幅度和相位信息两者结合,能够有效地对相位相同而幅度不同的两个类进行正确聚类。由图5还可看出,改进后的ART2网络能对离群点进行有效地识别,类别6表示该数据点与其他5个类的中心点的最短距离要大于设定的阈值R_dis,该数据点被作为离群点处理。
对原始数据有正有负的数据样本,由于传统的ART2网络存在输入域的限制,传统的ART2网络的F1层中将样本数据的非正实数抑制为0,因此传统的ART2网络不能将位于四个象限的数据样本进行有效的分类。改进后的ART2网络的非线性变换函数能处理负数的输入,并在F1层稳定后仍保持其负数形式,所以该网络还能对分别位于四个象限内的数据样本进行有效地聚类。
本文针对传统的ART2网络和改进后的ART2网络对分别位于四个象限的数据样本的聚类作了一个对比分析,数据样本是横、纵坐标在[-1,1]范围内随机生成的5个特征明显的类,每类包含30个数据样本进行聚类。网络的各个参数设置见表1。由图6可以看出,传统的ART2网络对位于四个象限内的数据样本的聚类效果很差,而图7是使用改进后的ART2网络对其进行聚类,显而易见,改进后的ART2网络可以对四个象限的数据进行很好的分类。
5 结论
通过上述理论和实验结果,表明本文提出的一种改进的ART2神经网络在处理相同相位的两个簇时,性能优于传统的ART2。该网络同时考虑了数据的相位信息和数据原型的幅度信息,并消除了离群点对聚类结果的影响。通过变换非线性变换函数,改进后的ART2网络能够处理负值数据,对四个象限的数据能够进行有效地聚类。通过实验表明改进的ART2网络在处理需要考虑幅度信息以及离群点的数据样本时性能要明显优于传统的ART2网络。
[1]Carpenter G A,Grossberg S.A massively parallel architecture for a self-organizing neural pattern recognition machine[J].ComputerVision,GraphicsandImageProcessing,1987,37(1):54-115.
[2]Carpenter G A,Grossberg S.ART-2:self-organization of stable category recognition codes for analog input pattern[J].Applied Optics,1987,26(23):4919-4930.
[3]Carpenter G A,Grossberg S.ART-3:hierarchical search usingchemicaltransmittersinself-organizingpattern recognition architectures[J].Neural Networks,1990,3(2):129-152.
[4]马锐,人工神经网络原理[M].北京:机械工业出版社,2010.
[5]Frank T,Kraiss K F,Kuhlen T.Comparative-analysis of fuzzy art and ART2A network clustering performance[J]. IEEE Trans on Neural Nerwork,1988,9(3):544-549.
[6]Li Liangjun,Zhang Bin,Che Yuanyuan.The improved algorithm of ART2 in data mining[C]//2009 1st International Workshop on Database Technology and Applications. Washington,DC:IEEE Computer Society,2009:177-180.
[7]顾民,葛良全.一种ART2神经网络的改进算法[J].计算机应用,2007,27(4):945-947.
[8]Hagan M T,Demuth H B.神经网络设计[M].戴葵,译.北京:机械工业出版社,2002.
[9]申岸伟,俞斌.一种提高ART-2神经网络分类器性能的方法[J].信号处理,1996,12(1):28-32.
[10]唐红卫,桑农,曹治国,等.ART-2神经网络的研究和改进[J].红外与激光工程,2004,33(1):101-106.
[11]徐永成,温熙森,易晓山,等.ART-2A的同相位不可分问题及其解决方法[J].数据采集与处理,2001,16(4):393-396.
[12]从爽,郑毅松,王怡雯.ART-2神经网络的改进及建模实现[J].计算机工程与应用,2002,38(14):25-27.
[13]黎明,严超华,刘高航.具有更严格警戒测试准则的ART-2神经网络[J].中国图象图形学报,2001,6(1):81-85.
[14]姚关顺.ART-2神经网络的缺点及其改进[J].仪器仪表用户,2008,15(2):112-113.
[15]杨兴,朱大奇,桑庆兵.一种改进的ART型神经网络学习算法[J].计算机技术与发展,2006,16(9):27-29.
CHEN Guocan,GAO Maoting
College of Information Engineering,Shanghai Maritime University,Shanghai 201306,China
While the matching measure of the pattern in clustering is only about the phase information and neglects the effects of the amplitude information of the patterns,traditional ART2 neural network can not cluster well for two clusters with the same phase but different amplitudes,and it also has limitation problem for inputs domain.As to the above disadvantages,an improved ART2 algorithm is put forward.The amplitude information of the patterns is also saved during the input pattern entering the network in the learning process,and the limitation is relaxed in a nonlinear transformation of negative numbers,and the shortest distance from the input pattern to the center of each cluster is taken into consideration. At the same time,a threshold to judge outliers is added to eliminate the influence of outliers on clustering results.Experimental results demonstrate that the performance of the improved ART2 is superior to the traditional ART2 when they cluster the two clusters with the same phase.
Adaptive Resonance Theory(ART)2 neural network;clustering;phase information;amplitude information
传统ART2神经网络在聚类过程中模式的匹配度量仅仅与模式的相位信息相关,这种匹配度量忽略了模式的幅度信息的作用,在对相位信息相同而幅度信息不同的两个簇进行聚类时,效果很差;同时,它还存在输入域限制的问题。针对这些不足之处,提出了一种改进的ART2神经网络,在输入模式进入网络学习过程中,保存其幅值信息,放宽对负实数的非线性转换,并考虑输入模式到各个簇的中心点的最短距离,同时增加一个阈值对离群点进行判定,消除了离群点对聚类结果的影响。实验验证,改进的ART2网络在对相同相位的两个簇聚类时,性能明显优于传统的ART2网络。
自适应共振理论(ART)2网络;聚类;相位信息;幅度信息
A
TP391
10.3778/j.issn.1002-8331.1210-0155
CHEN Guocan,GAO Maoting.Improvement for ART2 neural network.Computer Engineering and Applications, 2014,50(18):137-141.
上海市科委科技创新项目(No.12595810200);上海海事大学科研项目(No.201100051)。
陈国灿(1990—),男,硕士研究生,CCF学生会员,主要研究领域为数据挖掘;高茂庭(1963—),男,博士,教授,CCF高级会员,主要研究领域为数据挖掘、数据库与信息系统。E-mail:gcc1990@163.com
2012-10-16
2012-12-03
1002-8331(2014)18-0137-05
CNKI网络优先出版:2013-01-11,http://www.cnki.net/kcms/detail/11.2127.TP.20130111.1111.028.html

