Negative Differential Resistance of Au-MgB2-Au Nanoscale Junctions

Fu-ti Liu,Yan Cheng,Xiang-rong Chen

a.College of Physics and Electronic Engineering,Yibin University,Yibin 644000,China

b.Computational Physics Key Laboratory of Sichuan Province of Yibin University,Yibin 644000,China

c.College of Physical Science and Technology,Sichuan University,Chengdu 610064,China

Negative Differential Resistance of Au-MgB2-Au Nanoscale Junctions

Fu-ti Liua,b,c,Yan Chengc∗,Xiang-rong Chenc

a.College of Physics and Electronic Engineering,Yibin University,Yibin 644000,China

b.Computational Physics Key Laboratory of Sichuan Province of Yibin University,Yibin 644000,China

c.College of Physical Science and Technology,Sichuan University,Chengdu 610064,China

The electron transport of linear atomic chain of MgB2sandwiched between Au(100)electrodes was investigated by using the density functional theory with the non-equilibrium Green’s function method.We have calculated the corresponding cohesion energy and conductance of junctions in different distance.It is found that,at the equilibrium position,the Au-B bond-length is 1.90˚A,the B-Mg bond-length is 2.22˚A,and the equilibrium conductance is 0.51G0(G0=2e2/h).The transport channel is almost formed by the π antibonding orbitals,which was made up of the pxand pyorbital electrons of B and Mg atoms.In the voltage range of-1.5 to 1.5 V,the junctions show the metallic behaviors.When the voltage is larger than 1.5 V,the current decreases gradually and then negative differential resistance appears almost symmetrically on both positive and negative bias.

Electronic transport,MgB2atomic chain,Negative differential resistance

I.INTRODUCTION

The advent of nanotechnology made it possible to synthesize and manipulate even the ultimately thin wires made of single atomic chains[1].Low dimensional forms of materials can have properties quite different from those of their bulk structures.The existence of single atom chains was demonstrated using the scanning tunneling microscope and mechanically controllable break junctions where a quantized conductance close to G0=2e2/h for gold was measured,in agreement with previous theoretical predictions[2,3].The linear atomic chains of silicon display metallic I-V characteristics[4],the linear atomic chains of carbon is even a better conductor than gold chain[5,6].The conductance of monatomic chains of S,Ge,Sn elements,and of binary compounds such as InP,GaAs,AlSb,BN,SiC, GaN,AlN has been reported[7-10].The current voltage characteristics of nanodevices have shown profound potentials for device application,including high nonlinearity,negative differential resistance,and electron mechanic current switching.However,a thorough understanding of electron transport mechanisms at nanoscale has not yet been achieved[11].The bulk materials of MgB2were discovered to be a superconductor at a remarkably high critical temperature for its simple hexagonal structure.It will be a good material for electronic devices.During the past decades,MgB2has been synthesized in various forms:bulk,thin f i lms,powders, wires,tapes,as well as single crystals[12].The results show that the conductance of MgB2unit cell when the c axis is perpendicular to the directions of z axis(electronic transport direction)is larger than that when the c axis is parallel to the z axis direction[13].In order to provide insight into electron transport properties of MgB2,we examined the conductance of MgB2linear atomic chain attached to Au nanoscale leads using the density functional theory(DFT)combined with the non-equilibrium Green’s function method.

FIG.1 The MgB2linear atomic chain attached to Au(100)-3×3 leads.

II.THEORETICAL MODE AND METHODS

The theoretical model in this program is illustrated schematically in Fig.1.The physical model is comprised of MgB2linear atomic chain coupling with two semi-inf i nite Au(100)metal electrodes.The whole system can be divided into three regions:left and right leads,and a central extended molecule(scattering area), which includes seven and six Au atomic layers respectively at each side of the junction to screen the perturbation effect[14].In addition,in order to reduce the inf l uence of leads on the atomic chain,we design the pyramid-shaped electrodes at the top site with theatomic chain parallel to the transport direction(z-axis). The transport behavior is investigated by the ab initio transport code SMEAGOL[15-17],which calculates the density matrix and the transmission coefficients of a two probe device using the nonequilibrium Green’s function formalism.The scattering potential is calculated self-consistently using the SIESTA implementation of DFT[18].The left and right leads are considered perfect crystals,and the potential is well approximated by that of a perfect bulk electrodes.

The central quantity of the method is the retarded Green’s function of the entire system,which is def i ned by direct inversion of the equation

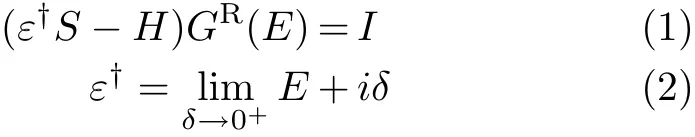
where E is the energy,S is the corresponding overlap matrix,H is the Hamiltonian matrix,I is the inf i nitelydimensional identity matrix.Because the interaction of molecule with electrodes can be incorporated into the self-energies(E),we can focus the attention on the calculation of the retarded Green’s function of the scattering region

The conductance G associated to the two-probe device can be calculated using the Fisher-Lee’s relation[19]:

where ΓL/Ris the anti-hermitian parts of self energy, e is electron charge and h is the Planck constant.The electron current can be calculated through the formula:

where f is electron distribution function of two electrodes,andµL/Ris chemical potential for the left/right electrode.More calculation details on how this procedure is performed in SMEAGOL can be found in Refs.[15,16,20].

In our calculations,we use the Perdew-Zunger version of the local density approximation to the exchangecorrelation functional[21].Valence electrons are expanded in single-zeta basis sets for Au atoms and double-zeta along with polarization basis sets for B and Mg atoms.Troullier-Martins pseudo potential in nonlocal form is generated[22].A periodic boundary condition is applied in the basal plane(orthogonal to the transport direction)with four irreducible k-points in the two-dimensional Brillouin zone.A k-grid sampling of 2×2×100 for the gold electrodes is employed.The cut-of fenergy and iterated convergence criterion for total energy is set to 200 Rydberg and 10-4,respectively. Furthermore,the charge density is integrated over 50 energy points along the semi-circle,20 energy points along the line in the complex plane and 20 poles are used for the Fermi distribution.

FIG.2 Conductance(G)and the cohesion energy(∆E)as a function of distance dz.

III.RESULTS AND DISCUSSION

In order to calculate the equilibrium structure under different distance,we perform geometry relaxation by keeping the bulk Au leads f i xed and relaxing the apexes of the point contact[23].The ground state energy is therefore calculated as a function of the distance dzbetween the outer slices(as shown in Fig.1),i.e.we simulate a junction breaking process.During the simulations of the junction breaking process,we calculate the junctions’conductance as a function of dz(shown in Fig.2).The conductance varies with dz.This demonstrates the sensitivity of the conductance to the local atomic re-arrangement of the contact region[24].Going into more details,as the junctions stretch,the conductance increases from 0.45G0at dz≈13.76˚A to 0.64G0at dz≈14.56˚A,then decreases to 0.26G0at dz≈16.96˚A, and increases again to 0.97G0at dz≈18.56˚A,then decreases abruptly to 0.07G0at dz≈19.76˚A,which is the B-Mg bond break-point.

In order to obtain the conductance of the junctions at the most stable structure in different distance,we calculate the cohesion energy as a function of dzduring the simulation process.The cohesion energy is def i ned as follows:

FIG.3 The total transmission coefficient T(E)and density of states(DOS)at zero bias.

The cohesion energy∆E as a function of dzis shown in Fig.2.In the range of 13.76-20.56˚A,there is a minimum value of the cohesion energy.The cohesion energy minimum is located at the equilibrium distances, dz,eq=15.36˚A.The distances dz,eqcorresponding to those minima describe the optimal position,that is to say,the system will naturally form if the leads are free to relax.When the junctions are in the optimal equilibrium positions,the Au-B bond length,dB-Au,is 1.90˚A,and dB-Mg=2.22˚A.The equilibrium conductance of MgB2chain at the optimal position is 0.51G0. The results indicate that the junctions of Au-MgB2-Au have good conductivity.

In order to gain a deeper understanding of the electronic transport properties of the junctions in the optimal position,we calculate the transmission coefficient T(E,V=0)and DOS in the energy range from-3.0 eV to 3.0 eV(shown in Fig.3).We can see that there are two molecular orbitals that contribute to electronic transport near the Fermi level(EF)of the chain.The transmission spectrum has good corresponding relation to the DOS.From the calculated results,we can know that T(E,V=0)is dominated by a resonance corresponding to the energy of the lowest unoccupied molecular orbital(LUMO).

In order to understand the structure of electronic transport channel,we calculate the projected density of states(PDOS)of B and Mg atoms in the chain. The results are shown in Fig.4.It is easy to see the transport channel is almost formed by the pxand pyorbital electrons of B and Mg atoms.Because that are perpendicular to the axis direction of the chain,they constitute the π antibonding orbitals,which is LUMO. This LUMO has important inf l uence on electron transport properties.The s orbital electrons of B and Mg atoms have the spherically symmetric characteristics, they interact along the direction of the atomic chain, forming the σ bonding orbitals,which is not very good for electronic transmission.So,its contribution to the transmission is very small.

FIG.4 The projected density of states(PDOS)of the chain at zero bias.

The results of relationship of current with external voltage are shown in Fig.5.We can see the junctions show the metallic behavior in the voltage range from -1.5 V to 1.5 V.This is due to the interaction between the chain and the metal electrodes,resulting in electrons of metal leads doped into the MgB2linear atomic chain [25].The most striking inf l uence is on the existence of negative differential resistance(NDR).When the external voltage is larger than 1.5 V,the current decreases gradually and then NDR phenomenon appears almost symmetrically on both positive and negative voltage ranges,which is due to the asymmetric structure of the junction.As we all know,NDR effect has many applications including high-speed switch,memory and amplifier[26].

To know more about the transport properties of the junctions,we now look at the dependence of transmission spectra T(E,V)on the external bias.As we know,the existence of external voltage will lead to the two leads maintain different chemical potential.So the junctions will be in the non-equilibrium states.From Eq.(5),we know that the current through junctions depends on the transmission amplitude within the bias window of[-V/2,V/2].In order to investigate nonequilibrium properties of this two-probe system,we calculate the transmission of the junctions under different voltage in the range from-2.0 V to 2.0 V.Figure 6 depicts the transmission of junctions when the voltage is 0,0.5,1.0,1.5,and 2.0 V,respectively.In the voltage range of 0-1.5 V,with the increase of external volt-age,the transmission peak is gradually near to the bias window and contributes to the transport current,which leads to a linear increase in the current.The junctions show the metallic behavior.However,when the voltage is larger than 1.5 V,the transmission amplitude in the bias window decreases rapidly.As a result,according to the Eq.(5)the total current of the chain decreases and NDR appears under large voltage.

FIG.5 The relationship of current with voltage.

IV.CONCLUSION

BasedontheDFTcombinedwiththenonequilibrium Green’s function method,we have studied the electron transport properties of MgB2in the form of linear atomic chain,which is sandwiched between Au(100)electrodes.To show the breaking process of Au-MgB2-Au junctions,we have calculated the corresponding cohesion energy and conductance of junctions in different distance.We f i nd that,when the Au-B bond-length in the junctions is 1.90˚A and Mg-B bond length is 2.22˚A,the cohesion energy of the junctions reaches the minimum,i.e.the chain is in the equilibrium position.The equilibrium conductance of junctions at this time is 0.51G0.From the calculated PDOS, we f i nd that the electron transport channel is almost formed by the π antibonding orbitals,which is made up of the pxand pyorbital electrons of B and Mg atoms.In order to obtain the transport properties of these junctions under different voltages,we have calculated the currents at different voltages ranging from -2.0 V to 2.0 V.It is found that the junctions show the metallic behaviors in the range of-1.5 V to 1.5 V. However,when the voltage is larger than 1.5 V,the current decreases gradually,and the negative differential resistance appears almost symmetrically on both positive and negative bias.These interesting physical properties motivate further experimental researches.It is expected that our theoretical predictions might be realized in future experiments.

FIG.6 The transmission of the chain under different voltage.The regions between the two vertical dashed lines stand for the bias window.

V.ACKNOWLEDGMENTS

This work was supported by the National NaturalScienceFoundationofChina(No.11174214 and No.11204192),the Research Project of Education Department in Sichuan Province(No.13ZB0207), and Scientific Research Project of Yibin University (No.2013YY05).

[1]D.R.Bowler,J.Phys.:Condens.Matter 16,R721 (2004).

[2]H.Ohnishi,Y.Kondo,and K.Takayanagi,Nature 395, 780(1998).

[3]J.Ferrer,A.Martın-Rodero,and F.Flores,Phys.Rev. B 38,R10113(1988).

[4]F.T.Liu,Y.Cheng,F.B.Yang,X.H.Cheng,and X. R.Chen,Chin.Phys.Lett.30,067302(2013).

[5]A.I.Yanson,G.Rubio-Bollinger,H.E.van den Brom, N.Agrait,and J.M.van Ruitenbeek,Nature(London) 395,783(1998).

[6]S.Tongay,R.T.Senger,S.Dag,and S.Ciraci,Phys. Rev.Lett.93,136404(2004).

[7]V.M.Garcia-Suarez,D.Z.Manrique,C.J.Lambert, and J.Ferrer,Phys.Rev.B 79,060408(2009).

[8]X.C.Chen,J.Yang,Y.H.Zhou,and Y.Xu,Acta Phys.Sin.58,3064(2009).

[9]J.X.Yu,Y.Cheng,S.Sanvito,and X.R.Chen,Appl. Phys.Lett.100,103110(2012).

[10]R.T.Senger,S.Tongay,E.Durgun,and S.Ciraci, Phys.Rev.B 72,075419(2005).

[11]J.Taylor,H.Guo,and J.Wang,Phys.Rev.B 63, 245407(2001).

[12]J.Nagamatsu,N.Nakagawa,T.Muranaka,Y.Zenitani, and J.Akimitsu,Nature(London)410,63(2001).

[13]F.T.Liu,S.H.Zhang,X.H.Cheng,and Y.X.Zhou, J.Henan Normal Univ.41,55(2013).

[14]J.Taylor,Ph.D.Dissertation,Montreal:McGill University of Canada,(2000).

[15]I.Rungger and S.Sanvito,Phys.Rev.B 78,035407 (2008).

[16]A.R.Rocha,V.M.Garcia-Suarez,S.Bailey,C.Lambert,J.Ferrer,and S.Sanvito,Nat.Mater.4,335 (2005).

[17]A.R.Rocha,V.M.Garcia-Suarez,S.Bailey,C.Lambert,J.Ferrer,and S.Sanvito,Phys.Rev.B 73,085414 (2006).

[18]J.M.Soler,E.Artacho,J.D.Gale,A.Garcia,J.Junquera,P.Ordejon,and P.D.Sanchez,J.Phys.:Condens.Matter 14,2745(2002).

[19]D.S.Fisher and P.A.Lee,Phys.Rev.B 23,6851 (1981).

[20]A.R.Rocha,Ph.D.Dissertation,Dublin:Trinity College of Ireland,(2007).

[21]J.P.Perdew,Phys.Rev.B 33,8822(1986).

[22]N.Troullier and J.L.Martins,Phys.Rev.B 43,1993 (1991).

[23]R.B.Pontes,A.R.Rocha,S.Sanvito,A.Fazzio,and S.A.Roqueda,ACS Nano 5,795(2011).

[24]I.S.Kristensen,D.J.Mowbray,K.S.Thygesen,and K.W.Jacobsen,J.Phys.:Condens.Matter 20,374101 (2008).

[25]D.Zhang,Y.Xu,J.Zhang,and X.Miao,Phys.Lett. A 376,3272(2012).

[26]B.A.Mantooth and P.S.Weiss,Proc.IEEE 91,1785 (2003).

ceived on March 13,2014;Accepted on May 20,2014)

∗Author to whom correspondence should be addressed.E-mail：ycheng@scu.edu.cn,futiliu@163.com