Insights into Elastic and Thermodynamics Properties of Binary Intermetallics in Ni-Al Alloys under Extreme Condition:Full-Electronic Quasi-Harmonic Study
Yong-song Luo,Yu-ping Cang,Dong Chen
College of Physics and Electronic Engineering,Xinyang Normal University,Xinyang 464000
Insights into Elastic and Thermodynamics Properties of Binary Intermetallics in Ni-Al Alloys under Extreme Condition:Full-Electronic Quasi-Harmonic Study
Yong-song Luo,Yu-ping Cang,Dong Chen∗
College of Physics and Electronic Engineering,Xinyang Normal University,Xinyang 464000
Atomistic modeling based on the accurate f i rst-principles method is used to investigate the lattice parameter,elastic constant,elastic modulus including bulk modulus(B)and shear modulus(G),Poisson’s ratio,and elastic anisotropy of Al,NiAl and Ni3Al under extreme condition.The elastic constants obtained from calculations meet their mechanical stability criteria.Both NiAl and Ni3Al exhibit ductile behavior due to their high bulk mudulus to shear modulus ratios of B/G ratios.Through the full-electronic quasi-harmonic approximation,in which the mobile electrons are considered,we successfully obtain the thermo-physical properties including the thermal expansion coefficient,bulk modulus,heat capacity and entropy at simultaneously high temperatures and high pressures.The calculated quantities agree well with the available results.Some silent results are also interpreted.Several interesting features in the thermodynamic properties can also be observed.
First-principles,Heat capacity,Bulk modulus,Debye approximation
I.INTRODUCTION
Due to the valuable properties such as light weight, high elastic moduli,good corrosion resistance,excellent thermal conductivity,and large plasticity[1],Al,NiAl, and Ni3Al are especially amenable to be used in space project.As a metallic element without d-electrons,a relatively low atomic mass and a simple structure,Al can be used as a reference material in modern industry. It has been known for several decades that aluminum has a face-centered cubic structure at room temperature (space group:Fm-3m).Al can retain its mechanical stability up to 220 GPa[2].Upon further compression, it will transform into a new phase,which has a hexagonal close-packed structure(hcp-Al)[2,3].The Ni-Al binary alloys have been used as high-temperature materials for gas turbines and aircraft engines.These alloys also belong to the engineering materials with attractive properties including good high-temperature strength, resistance to oxidation and low density[4,5].The Ni-Al alloys for structural applications in energy conversion systems are currently under development[6-9].NiAl and Ni3Al crystallize in cubic structures(space group: Pm-3m).The Ni and Al atoms(NiAl)occupy the(0.5, 0.5,0.5)and(0,0,0)Wyckof fpositions[4],respectively. Different atoms in Ni3Al occupy the Al(0,0,0)and Ni (0.5,0,0.5)sites[10].
First-principles technique including lattice dynamics and phonon approaches has been widely used and are now indispensable for condensed-matter physics.One shortcoming is that the pressure and temperature effects can not be simultaneously considered.Blanco et al.have developed a“quasi-harmonic Debye”approach (QHD)[11],in which some fundamental thermal properties of solids can be obtained at high temperature and high pressure.Unfortunately,the QHD scheme is not suitable for metals since the mobile electron contributions to the Gibbs free energy are not taken into account in this scheme.As an all-known fact,there are many free electrons in metals and alloys.These highly mobile electrons can not be ignored,especially at high temperatures.
The temperature and pressure dependences of thermodynamic quantities can directly provide useful information for understanding the dynamical response of solids[12].Although the elastic and thermodynamic properties of Al,NiAl and Ni3Al have been widely investigated from experiment[6,8,13-15]to theory[7, 16-23],the pressure P was often restricted to 0 GPa and the mobile electron contributions were usually ignored.Take Ni as an example,the electronic contribution to the heat capacity was 28%of heat capacity at 1000 K[19].
In this work,we investigate the thermodynamic properties of NixAl(x=0,1 and 3)at simultaneously high temperature and high pressure by the recently developed full-electronic quasi-harmonic approximation(FEQHA)sheme to obtain the high-temperature and highpressure properties of solids,the mobile electrons areconsidered at high pressures and high temperatures.
II.METHOD OF CALCULATION
We fi rstly do the total energy calculations by performing the fi rst-principles plane-wave pseudo-potential (PW-PP)method[24].The exchange-correlation functional is treated by the generalized gradient approximation(GGA)of the PBE form[25].Reference confi gurations for the valence electrons are Ni3d84s2and Al3s23p1.According to the convergence tests,the cuto ffenergies are chosen to be 500 eV.The Monkhorst-Pack k-points[26]are 14×14×14,15×15×15,and 15×15×15 for Al,NiAl,and Ni3Al,respectively.The convergence of the total energy is 0.2µeV/atom.The phonon density of state is calculated through the finite displacement method combined with the normconserving pseudo-potentials[27].For the ˚super-cell(48unit cells),we use a cuto ffradius of 5.0A in order to obtain the accurate results.The q-vector is chosen to be 9×9×9.For such simple structures,these parameters are suitable for the phonon calculations.
Thek-pointsaredeterminedbytheequation (1/a:1/b:1/c),where a,b,and c are the lattice constants.For the cubic Al,NiAl,and Ni3Al,the 1/a:1/b:1/c=1:1:1.The k-point mesh should be 3×3×3, or 4×4×4,or 11×11×11,etc.According to our convergence tests,the plane-wave cuto ff500 eV and the kpoints 14×14×14 can generate good results for Al.The adequate parameters for NiAl and Ni3Al are found to be 500 eV(cuto ffenergy)and 15×15×15(k-points).
The main advantage of the calculation of pressure and temperature dependent properties of solids is the easiness with which extreme conditions,unattainable by experimental means,can be modeled and determined.Then FEQHA sheme is implemented to obtain the high-temperature and high-pressure properties of solids.This method has been described in detail elsewhere(see Refs.[28,29]),here we give a brief overview for completeness.In the FEQHA scheme,the nonequilibrium Gibbs free energy G∗(V;P,T)can be determined by

where E(V)is the total energy.PV represents the hydrostatic pressure condition.Fviband Felare the contributions to the Helmholtz free energy from atomic vibrations and mobile electrons,respectively.


where kBis the Boltzmanns constant,T the temperature,n(ε,V)the electronic DOS,f(ε)the Fermi function,ωjthe vibrational frequency,εFthe total density of states at Fermi energy level,n the number of atoms,and N the number of cells in the macroscopic solid[19].Thermal properties such as heat capacity CV, CP,isothermal bulk modulus BT,adiabatic bulk modulus BS,thermal expansion coefficient α,Gr¨uneisen ratio γ and entropy S can be deriven from Eq.(1)

The advantages of the FEQHA scheme are:(i)wide ranges of temperature and pressure conditions are considered,(ii)only a few calculation parameters are included in this approach.Up to now,the magnetic energies of solids are not considered in the QHA and FEQHA methods.Therefore,these methods are not suitable for transition metals and the corresponding alloys.On the other hand,the high-temperature results obtained by QHA near the melting point Tm(T-Tm<100 K)have not been verified by experiments. The disadvantage of QHA,however,is that most of the parameters are nonlinear and starting from a good set of values is usually a requirement for achieving the convergence of the total energies.Appling the FEQHA model,the real situations inside solids can be simulated well since the mobile electrons are included.
III.RESULTS AND DISCUSSION
A.Crystal structures and elastic properties
The schematic crystal structures and different atomic coordinations of Al,NiAl and Ni3Al are plotted in Fig.1. The pressure effect on the elastic constants is essential, especially for understanding the chemical interaction and mechanical stability,and for for developing interatomic potentials.Therefore,the dependences of the elastic constants on pressure for Al,NiAl and Ni3Al are calculated and listed in Tables I and II.According to theVoigt-Reuss-Hill(VRH)approach[30],the bulk modulus B,shear modulus G,Young’s modulus E,Poisson’s ratio σ,and Zeners elastic anisotropy factor A for the cubic crystal can be determined by the following equations[6,22]

TABLE I Lattice constant a,elastic constants Cij,bulk modulus B,shear modulus G,Young’s modulus E,Poisson’s ratio σ and Zeners elastic anisotropy A of Al.

TABLE II Lattice constant a,elastic constants Cij,bulk modulus B,shear modulus G,Young’s modulus E,Poisson’s ratio σ and Zeners elastic anisotropy A of NiAl and Ni3Al.
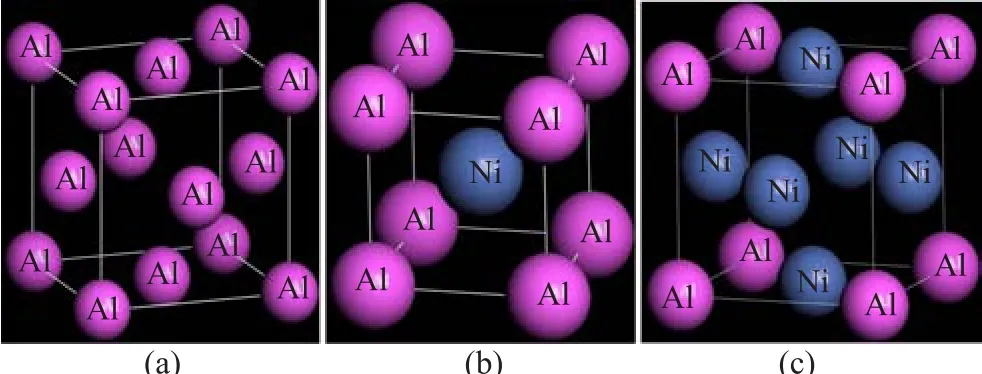
FIG.1 Crystal structures and atomic arrangements of (a)Al,(b)NiAl,and(c)Ni3Al.

As shown in Table I,the lattice constant a,elastic constants Cij,elastic modulus B,G and E of Al are consistent with the experimental data as well as with the theoretical results.The elastic constants and elastic moduli increase with applied pressure while a shows the opposite trend.The slopes of these quantities are different.C11is more sensitive to pressure than C12and C44.At 0 GPa,the discrepancy between the calculated Cijand the experimental data[31,32]is mainly due to: (i)GGA typically underestimates the elastic constants; (ii)the experimental data are obtained at room temperature while f i rst-principles results are restricted to 0 K;(iii)The measurements of Cijfrom polycrystalline samples include defects and porosities.In our scheme, the calculations are related to ideal crystals.The Born and Huangs stability criteria[36](C11+2C12>0,C44>0, C11-C12>0 and C11>B>C12)are satisfied by the elastic constants listed in Table I.Therefore,Al can retain its cubic structure in the pressure range of 0-200 GPa. σ decreases f i rst,and then increases or decreases unorderedly when the pressure exceeds 80 GPa.It is worth noting that the PW-PP bulk moduli agree well with the FEQHA bulk moduli,which have partially proven the reliability of our calculation.
As it can be seen in Table II,C11and C12of NiAl and Ni3Al increase monotonically and rapidly with applied pressure while C44increases slowly with pressure increasing.All B,G and E increase with the increasing pressure,but the slopes are different.σ is larger than 0.327(0.334)for NiAl(Ni3Al)and gradually increases with applied pressure.Cijsatisfies the Born and Huangs criteria[36],which suggests that the cubic NixAl(x=1,3)are stable below 30 GPa.The elastic anisotropy can be conveniently expressed by a dimensionless parameter A,which is called Zeners elastic shear anisotropy factor.A=1 ref l ects the isotropic character of a crystal,but a majority of solids show elastic anisotropy(A/=1).For NiAl,A increases with the increasing pressure up to 10 GPa whereas it decreases linearly in the pressure range of 10-30 GPa.Ni3Al is little anisotropic and somewhat insensitive to pressure. Besides,the anisotropy of Al(see Table I)increases rapidly with pressure when P<40 GPa and gradually becomes less anisotropic upon further compression.
Pugh introduced the B/G ratio characterized as an indication of brittle versus ductile[38].If B/G>1.75, the material exhibits a ductile manner,otherwise,it behaves in a brittle character.Besides,the smaller the B/G ratio is,the stronger the material hardness will be. The B/G ratio indicates that NiAl and Ni3Al are ductile alloys.The ductility increases with the increasing pressure.NiAl is harder than Ni3Al at a f i xed pressure. As can be seen in Table I,Al is a brittle material at 0 GPa,but it behaves in ductile manner in the pressure range of 40-200 GPa.Our calculated zero-pressure lattice constant of NiAl agrees well with the theoretical values(0.2918˚A[7],0.2895˚A[39])and the experimental data(0.2880˚A[40]).The lattice constant of Ni3Al is also in excellent agreement with the theoretical results (0.3568˚A[10],0.3574˚A[22])and the experimental data (0.3572˚A[41]).All the values listed in Table II are in agreement with the results reported in Refs.[6,22,37] except C44and A of Ni3Al.Unfortunately,the exact reason for this discrepancy is still unclear.
B.Thermal properties
Since NixAl(x=0,1 and 3)are potential materials for satellite components and deoxidizers,it is necessary to investigate the thermal properties of Al,NiAl and Ni3Al under extreme conditions.For the NiAl and Ni3Al alloys,the Debye-Grneisen model is used in the FEQHA scheme.
Figure 2(a)displays the temperature dependence of α for Al via different methods.After a sharp increase, up to 300 K,α reaches a linear region in the temperature range of 300-900 K.It can be clearly seen that the FEQHA results are closer to the experimental data[42] in the temperature range of 0-400 K compared with the QHD results.The results of these two approaches agree well with the experimental data[42]at temperatures higher than 400 K.In Ref.[19],the computed α of Al,Ni,NiAl and Ni3Al are often larger than the experimental data at high temperature.Generally speaking, our FEQHA results are more reliable than the QHD results since the electron contributions are taken into account in the FEQHA approach.As shown in Fig.2(b), the behavior of α is quite different.The 0 GPa-curve has a parabolic behavior while the 200 GPa-curve shows almost linear dependence on temperature.α decreases rapidly as the pressure increases.The temperature effect becomes less important.
Figure 2(c)and(d)illustrate the pressure and temperature effects on the thermal expansion coefficient α of NiAl and Ni3Al,respectively.Both pressure and temperature are important for α.At a given temperature, α increases with the decreasing pressure.At a f i xed pressure,α increases sharply with the increasing temperature below 400 K.Then,the rate decreases in the temperature range of 400-1300 K.The calculated thermal expansion coefficients of NiAl and Ni3Al are basically closer to the reported experimental data[42]compared with the theoretical results given in Ref.[19].At high temperatures,Al has the greatest α while Ni3Al has the lowest α.The thermal expansiondecreases with the subscript x of the NixAl crystal.

FIG.2(a)Temperature dependence of α for Al.Variations of α with temperature and pressure for(b)Al,(c)NiAl,and (d)Ni3Al.

FIG.3 (a)Temperature dependence of CPfor Al at 0 GPa.(b)Variations of CPfor Al with temperature at 40,80,120, 160,200 GPa.(c)Temperature dependences of CPfor NiAl and Ni3Al at 0 GPa.(d)Pressure dependences of CPfor NiAl and Ni3Al.

FIG.4 Variations of CVfor Al with temperature and pressure.
The isobaric heat capacity CPand isochoric heat capacity CVof Al,NiAl and Ni3Al on the temperature and pressure dependences are drawn in Fig.3 and Fig.4, repectively.As shown in Fig.3(a),CPincreases quickly at low temperature and tends to zero when the temperature vanishes.Then,CPgradually reaches a linear region(T>400 K)and the propensity of increment becomes gentler.One can also notice that the FEQHA results are rather in good agreement with the experimental data[16]and the theoretical results[17,33] compared with the QHD results.It is found in Fig.3(b) that CPis dependent on both temperature and pressure.CPincreases with the temperature at a given pressure,and decreases with the pressure when the temperature is f i xed.The temperature effect on CPis much more significant than that of pressure.As shown in Fig.4,CVfollows the Debye T3law at low temperatures. CVand CPshow roughly similar behaviors in the entire ranges of pressure 0-200 GPa and the temperature 0-700 K.Unlike the isobaric heat capacity curves,the CVcurves obey to the Dulong and Petits classical law (24.94 J/(mol K):CV~3R for monoatomic materials) at high temperatures while CPfollows a linear increase with the temperature increasing.
In Fig.3(c),CPshows a sharp increase up to 300 K, and then CPincreases almost linearly with the temperature increasing.The CPvalues of Ni3Al are larger than those of NiAl before the cross point(at 600 K). It is seen from Fig.3(d)that CPdecreases at the given temperature when the pressure increases.The inf l uences of the temperature on CPare much more signif icant than that of the pressure on it.The calculated CPfor Ni3Al are 90.2,97.8,100.9 and 102.7 J/(mol K)at temperatures of 300,500,700 and 900 K,respectively. These values are in agreement with the experimental data of 97.9(300 K),103.7(500 K),109.3(700 K)and 115.6 J/(mol K)(900 K)[23].The calculated CPare consistent with Shang et al.’s results[23],which ref l ects that our results are reliable.
Figure 5(a)shows the temperature dependences of the isothermal bulk modulus BT(BT(P=0)=B)and adiabatic bulk modulus BSfor Al.One can see that BTand BSare nearly constant from 0 K to 100 K,which indicates that the temperature effect on bulk modulus is trivial.This is due mainly to the fact that the atomic vibrations in the unit cell are not significant in the temperature range of 0-100 K.As calculated obviously from Eq.(9),BTand BScoincide at zero temperature and diverge more and more when the temperature increases.BSdecreases moderately and smoothly with the temperature increasing.The negative slopes of the curves demonstrate that Al becomes more and more compressible when T is applied and the compressibility increases with the increasing temperature.It is the rapid volume variation that makes BTrapidly decrease. The calculated BSare 74.9,71.4,67.4,and 62.7 GPa at temperatures of 300,500,700,and 900 K,respectively. These results are in good agreement with the experimental BSvalues of 76.1(at 300 K),72.5(at 500 K), 68.3(at 700 K)and 63.9 GPa(at 900 K)[43].
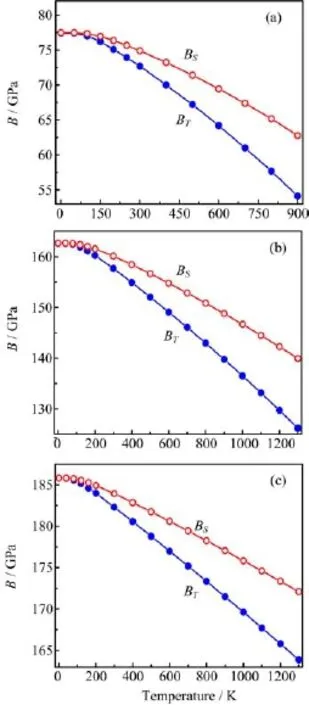
FIG.5 The temperature dependences of adiabatic bulk modulus BSand isothermal bulk modulus BTfor(a)Al, (b)NiAl,and(c)Ni3Al.
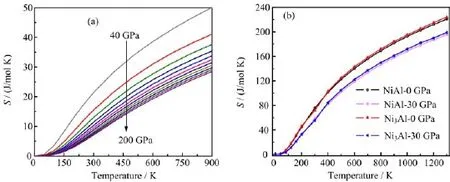
FIG.6 The temperature dependences of entropy S for(a)Al at 0,20,40,60,80,100,120,140,160,180,and 200 GPa shown as the arrow indicates,(b)NiAl and Ni3Al.
It can be clearly seen from Fig.5(b)and(c)that the temperature dependences of BSand BTfor NiAl,and Ni3Al are quite similar to the curves drawn in Fig.5(a). In the temperature range of 0-1300 K,BS(BT)decreases by 19.01%(30.10%),13.96%(22.38%),and 7.37%(11.84%)for Al,NiAl,and Ni3Al,respectively. Therefore,the temperature effect on the compressibility of NiAl is weaker than that of Al,but stronger than that of Ni3Al.Since Eq.(9),errors in the higher-order thermal parameters(the thermal expansion coefficient α and the Gr¨uneisen parameter γ)will lead to larger errors in the isothermal bulk modulus BT.As shown in Fig.5(c),the calculated BT(Ni3Al)are 183.9,178.4 and 171.2 GPa at temperatures of 300,700 and 1300 K,respectively.These results agree well with the theoretical values of 173.9(300 K),164.5(700 K)and 151.8(1300 K)[23].More importantly,the FEQHA bulk moduli of the three alloys are in agreement with the PW-PP bulk moduli listed in Tables I and II.
In Fig.6(a),the entropy S of Al is very small below 100 K.Between 100 and 900 K,the entropy,as expected,increases quickly with the increasing temperature.When the pressure increases from 0 to 200 GPa, the entropy S decreases at constant temperature.The effect of increasing the temperature is similar to decreasing the pressure.The entropy S drawn in Fig.6(b) shows the same performance as the entropy illustrated in Fig.6(a).S is variable by power exponent with the temperature increasing.Ni3Al has greater entropies compared with NiAl.The temperature effect on S is much more significant than the pressure effect on S. Our calculated entropies for Ni3Al are 0.88 at 40 K, 71.94 at 300 K and 184.79 J/(mol K)at 900 K,agreeing with the theoretical results of 0.99 at 40 K,97.37 at 300 K and 215.17 J/(mol K)at 900 K[23].
IV.CONCLUSION
The structural,elastic and thermodynamic properties of the typical metal Al and its alloys(NiAl,Ni3Al) have been investigated through the accurate planewave pseudo-potential method combined with the fullelectronic quasi-harmonic approximation(where the highly mobile electrons are included).The agreement between our calculated lattice constants/elastic constants and the other results is good.All the elastic constants meet the mechanical stability criteria.B/G ratios are well above 2.56 suggesting NiAl and Ni3Al as ductile.Ni3Al is little anisotropic and somewhat insensitive to pressure.Both NiAl and Al have strong elastic anisotropies.The bulk modulus,heat capacity, thermal expansion coefficient and entropy of Al,NiAl and Ni3Al are predicted at simultaneously high temperatures and high pressures.The results show that Al has the greatest thermal expansion cofficient while Ni3Al has the lowest one.Ni3Al has greater entropies compared with NiAl.Some interesting features in these quantities can be observed at high temperatures.
The agreement between our computed thermal properties and the available experimental data indicates that the FEQHA approach can predict blindly the behaviors of Ni-Al alloys in regions beyond the experimental limits.Nevertheless,our results are all predictions and need to be verified by the future experiments.
陈林曾发文讲述这段历程:当时的宏远队中,李春江是从辽宁来的,黄云龙是从八一过来的,张勇军来自湖北,李青山来自黑龙江,关德友是吉林的。从球员组成来讲,可以说是“散兵游勇”。因此宏远队也有另一个称谓:“雇佣军”。
V.ACKNOWLEDGEMENTS
This work was supported by the National Natural Science Foundation of China(No.U1204501,No.11304141, No.11105115).We thank Prof.Alberto Qtero-de-la-Roza and his colleague for the FEQHA model(Gibbs2 code).We also acknowledge Prof.M.A.Blanco and his co-workers for their QHD model(Gibbs code).
[1]T.G.White,S.Richardson,B.J.B.Crowley,L.K. Pattison,J.W.O.Harris,and G.Gregori,Phys.Rev. Lett.111,175002(2013).
[2]J.C.Boettger and S.B.Trickey,Phys.Rev.B 53,3007 (1996).
[3]R.G.Greene,H.Luo,and A.L.Ruof f,Phys.Rev.Lett. 73,2075(1994).
[4]J.Q.He,Y.Wang,M.F.Yan,Y.Yang,and L.Wang, Comput.Mater.Sci.50,545(2010).
[5]S.He,P.Peng,L.Peng,Y.Chen,H.Wei,and Z.Q. Hu,J.Alloys Compd.597,243(2014).
[6]G.Frommeyer,R.Rablbauer,and H.J.Sch¨afer,Intermetallics 18,299(2010).
[7]H.Z.Fu,Z.F.Hou,J.Fu,and Y.M.Ma,Intermetallics 42,156(2013).
[8]Z.F.Zhang,B.Gleeson,K.Y.Jung,L.Li,and J.C. Yang,Acta Mater.60,5273(2012).
[9]J.Zhang,Z.Chen,X.J.Du,C.Chen,and T.Yang, Superlattices Microstruct.52,834(2012).
[10]A.Hussain,S.Aryal,P.Ruils,M.A.Choudhry,J. Chen,and W.Y.Ching,J.Alloys Compd.509,5230 (2011).
[11]M.A.Blanco,E.Francisco,and V.Lua˜na,Comput. Phys.Commun.158,57(2004).
[12]D.W.He,Y.S.Zhao,L.L.Daemen,J.Qian,K.Lokshin,T.D.Shen,J.Zhang,and A.C.Lawson,J.Appl. Phys.95,4645(2004).
[13]A.R.Shirani Bidabadi,M.H.Enayati,E.Dastanpoor, R.A.Varin,and M.Biglari,J.Alloys Compd.581,91 (2013).
[14]P.S.Ho and A.L.Ruof f,J.Appl.Phys.40,3151 (1969).
[15]N.W.Ashcroft and N.D.Mermin,Solid State Physics, New York:Rinehar and Winston,(1976).
[16]R.C.Shukla and C.A.Plint,Int.J.Thermophys.1, 299(1980).
[17]S.Raju,K.Sivasubramanian,and E.Mohandas,Solid State Commun.122,671(2002).
[18]Y.P.Varshni and R.C.Shukla,J.Chem.Phys.43, 3966(1965).
[19]Y.Wang,Z.K.Liu,and L.Q.Chen,Acta Mater.52, 2665(2004).
[20]A.Debernardi,M.Alouani,and H.Dreyss´e,Phys.Rev. B 63,064305(2001).
[21]S.K.Xiang,L.C.Cai,and F.Q.Jing,Phys.Rev.B 70,174102(2004).
[22]H.Hou,Z.Q.Wen,Y.H.Zhao,L.Fu,N.Wang,and P.Han,Intermetallics 44,110(2014).
[23]S.L.Shang,Y.Wang,D.E.Kim,and Z.K.Liu,Comput.Mater.Sci.47,1040(2010).
[24]W.Kohn and L.J.Sham,Phys.Rev.140,A1133 (1965).
[25]J.P.Perdew,K.Burke,and M.Ernzerhof,Phys.Rev. Lett.77,3865(1996).
[26]H.J.Monkhorst and J.D.Pack,Phys.Rev.B 13,5188 (1976).
[27]G.J.Ackland,M.C.Warren,and S.J.Clark,J.Phys.: Condens.Matter 9,7861(1997).
[28]A.Otero-de-la-Roza and V.Lua˜na,Comput.Phys. Commun.182,1708(2011).
[29]A.Otero-de-la-Roza and V.Lua˜na,Comput.Phys. Commun.182,2232(2011).
[30]R.Hill,Proc.Phys.Soc.A 65,349(1952).
[31]G.N.Kamm and G.A.Alers,J.Appl.Phys.35,327 (1964).
[32]K.Hachiya and Y.Ito,J.Alloys Compd.337,53 (2002).
[33]D.R.Lide,Handbook of Chemistry and Physics,New York:CRC Press,(1998).
[34]R.Gaudoin,W.M.C.Foulkes,and G.Rajagopal,J. Phys.:Condens.Matter 14,8787(2002).
[35]B.K.Panda,C.D.Beling,and S.Fung,Phys.Rev.B 50,5695(1994).
[36]M.Born and K.Huang,Dynamical Theory of Crystal Lattices,Oxford:Clarendon,(1954).
[37]H.Yasuda,T.Takasugi,and M.Koiwa,Acta Metall. Mater.40,381(1992).
[38]S.F.Pugh,Philos.Mag.45,823(1954).
[39]N.I.Papanicolaou,H.Chamati,G.A.Evangelakis,and D.A.Papaconstantopoulos,Comput.Mater.Sci.27, 191(2003).
[40]Y.I.Dutchak and V.G.Chekh,Russ.J.Phys.Chem. 55,1326(1981).
[41]P.M.Rao,S.Suryanarayana,K.S.Murthy,and S.N. Naidu,J.Phys.:Condens.Matter 1,5357(1989).
[42]Y.S.Touloukian,R.K.Kirby,R.E.Taylor,and P. D.Desai,Thermal Expansion:Metallic Elements and Alloys,New York:Plenum Press,(1975).
[43]D.Gerlich and E.S.Fisher,J.Phys.Chem.Solids 30, 1197(1969).
ceived on April 27,2014;Accepted on June 16,2014)
∗Author to whom correspondence should be addressed.E-mail:chchendong2010@163.com,FAX:+86-376-6391731
 CHINESE JOURNAL OF CHEMICAL PHYSICS2014年4期
CHINESE JOURNAL OF CHEMICAL PHYSICS2014年4期
- CHINESE JOURNAL OF CHEMICAL PHYSICS的其它文章
- Exchange Bias Effect in Phase Separated La0.33Pr0.34Ca0.33MnO3Thin Films
- Elasticity and Thermodynamic Properties of EuS Related to Phase Transition
- Corrosion Study on Tantalum in Anhydrous Ethanol
- Kinetics Study on O2Adsorption and OHadDesorption at Pt(111),Its Implication to Oxygen Reduction Reaction Kinetics
- Phase Transition Behaviour of VO2Nanorods
- Effect of Molybdenum Doping on Oxygen Permeation Properties and Chemical Stability of SrCo0.8Fe0.2O3-δ
