A Two-step Design Method for Shaft Work Targeting on Low-temperature Process*

LUO Yiqing (罗祎青)**, FENG Shengke (冯胜科) SUN Changjiang (孙长江)and YUAN Xigang (袁希钢)School of Chemical Engineering and Technology, Tianjin University, Tianjin 30007, ChinaBeijing Risun Chemical Technologies Institute Company Limited, Beijing 00070, China

A Two-step Design Method for Shaft Work Targeting on Low-temperature Process*

LUO Yiqing (罗祎青)1,**, FENG Shengke (冯胜科)1, SUN Changjiang (孙长江)2and YUAN Xigang (袁希钢)11School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China2Beijing Risun Chemical Technologies Institute Company Limited, Beijing 100070, China

In low-temperature processes, there are interactions between heat exchanger network (HEN) and refrigeration system. The modification on HEN of the chilling train for increasing energy recovery does not always coordinate with the minimum shaft work consumption of the corresponding refrigeration system. In this paper, a systematic approach for optimizing low-temperature system is presented through mathematical method and exergy analysis. The possibility of “pockets”, which appears as right nose section in the grand composite curve (EGCC) of the process, is first optimized. The EGCC with the pockets cutting down is designed as a separate part. A case study is used to illustrate the application of the approach for a HEN of a chilling train with propylene and ethylene refrigerant system in an ethylene production process.

exergy, shaft work, heat exchanger network, cold pocket, low-temperature process, optimization

1 INTRODUCTION

The heat exchanger network (HEN) and the refrigeration system in a low-temperature process are interlinked and their interactions are complex because compressor power is involved in utility requirements as well as heat in the system [1]. There are several methods for optimizing HEN in low temperature in recent years, almost all of which try to recover more heat energy in HEN [2]. However, since different level cold utility is supported by the refrigeration compressor, although these methods can recover most of heat energy in HEN, the refrigeration shaft work is usually not optimal and the optimization for whole system cannot be guaranteed. In a low-temperature process, the refrigeration shaft work should be the final target in optimizing the whole system [3, 4]. The pinch analysis method [5] can set heat load targets, but it is difficult to optimize the shaft work target simultaneously. Linnhoff and Dhole [6] had introduced the concept of “shaft work targets”, which allows the designer to obtain quantitive changes in the refrigeration shaft work requirement with exergy analysis [7] and bypass the exact design of both HEN and refrigeration system. To show the exergy loss in a heat exchanger network, carnot factor has been used to form the grand composite curve (EGCC) as shown in Fig. 1 [8-10],

where ηcis the carnot efficiency and T0is the environment temperature. In Fig. 1 the shaded area between curves is proportional to the exergy loss in the HEN and is denoted as (σT0)HEN[8, 11]. Thus the amount of ideal work equivalent lost in heat transfer is proportional to the shaded area. When the reduction of shaded area is (σT0)HEN, the reduction of the shaft work is

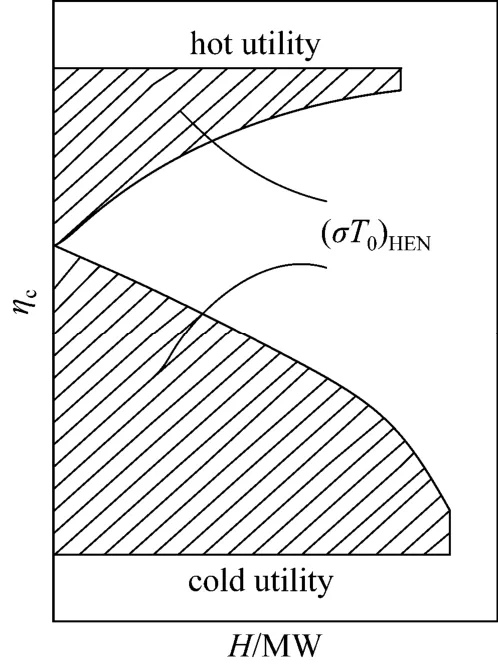
Figure 1 Exergy grand composite curve

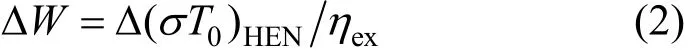
where ηexis the exergetic efficiency of refrigeration system, which is approximately constant [12] and is 0.59 here.

However, as shown in Fig. 2, there are always pockets in the EGCC. If the energy in pockets and the temperature difference of the hot and cold streams in the pocket are both large [13], it is worthwhile to recover the energy in the pocket to improve the energy efficiency of the system. In this study, a two-step method is introduced to reduce the shaft work of a low-temperature process. First, cold pockets in the EGCC will be optimized in order to recover high quality utility. Then a mathematical method will be used to optimize the optimal utility arrangement. AHEN of a chilling train with propylene and ethylene refrigerant cycle process, with several cold pockets below the pinch of its EGCC, is used as a case study to specify the significant economic benefits.

Figure 2 EGCC with pocket

2 OPTIMIZATION METHOD

In a low-temperature process, the EGCC always contains some pockets. A two-step method is adopted to optimize the process.

2.1 Optimizing cold pockets

Figure 3 shows the principle of optimizing cold pockets. A lower quality utility “EB” is used to exchange heat with the hot streams. Then, cold streams are used to generate a higher quality utility “FC”, and its temperature is decided by the minimum temperature difference of heat transfer. According to Linnhoff, the reduction of the exergy loss is proportional to the area of “EBCF”, namely Δ(σT0)HEN,P.

Figure 3 Cold pockets in the EGCC

2.2 Optimizing the low-temperature process without pockets

Figure 4 shows the EGCC without pockets after optimizing the cold package of “EBCF”, and a mathematical method is then used to obtain the optimum utility setting for the system. The level as well as the number of cold utilities is chosen as optimization variables, and the shaded area between the cold utilities and the process streams is the objective for minimization.

The mathematical model is presented as

where N is the number of cold utilities, Hirepresents the enthalpy supplied by cold utility at temperature level i, ηciis the carnot factor at temperature level i, Hminand Hmaxrepresent the minimum and maximum enthalpy in the EGCC, respectively, S is the original loss of exergy, which is represented by the shaded area in Fig. 4. The optimization problem can be solved using a particle swarm optimization (PSO) [14] algorithm, which is a population based stochastic optimization technique. In PSO, the potential solutions, named as particles, fly through the problem space following the current optimum particles. As a point in a D-dimensional space, each particle updates according to its own experience and of other particles. The algorithm is simple in concept and can give good results in a faster and cheaper way. A PSO algorithm [15] is implemented and is illustrated in Fig. 5, where k is the number of iteration, ω, c1and c2are positive constants, v is the set of rate of position change of particle, and T is a set of temperature levels needed to be optimized for all particles.

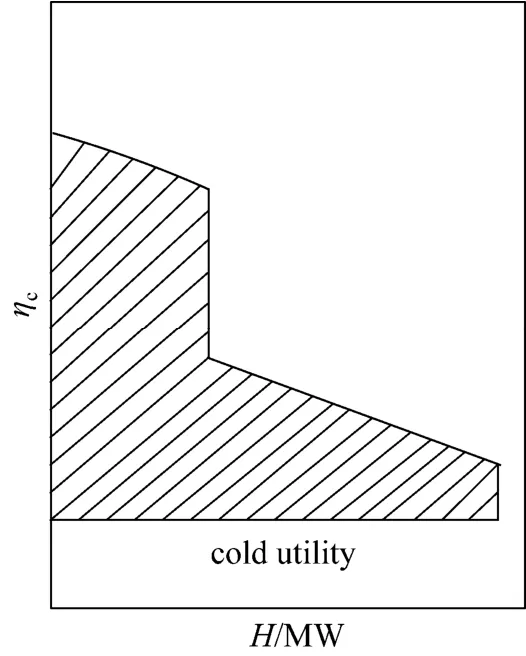
Figure 4 EGCC without pockets

Figure 5 The methodology framework

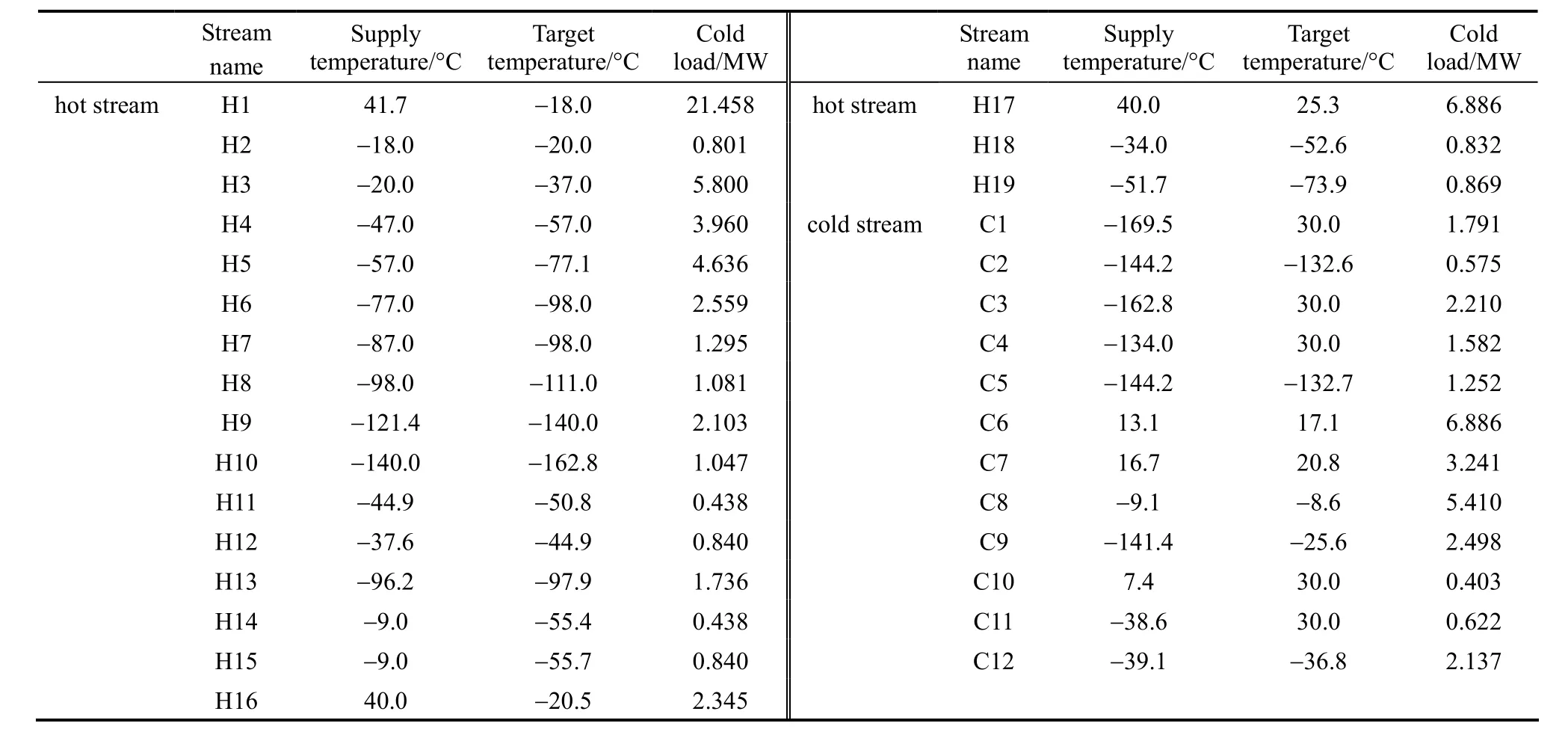
Table 1 Stream data of the HEN

3 CASE STUDY

The stream data shown in Table 1 belong to a HEN of a chilling train in an ethylene plant. The value of T0in Eq. (1) is 298.15 K. Fig. 6 is the EGCC for the process with vertical axis ηc. The original cold utilitiesare shown in Table 2, where P represents the propylene refrigerant and E represents the ethylene refrigerant. By calculating the area between the EGCC and the cold utilities, we get the exergy loss 2.659 MW. Then the two-step method is adopted to optimize the process.

Figure 6 shows the pockets for the system. We optimize the pocket as shown in Fig. 7, in which both the energy and the temperature difference of the hot and cold streams are large. Here, the minimum temperature difference of heat transfer is taken as 3.0 °C. A lower quality utility is used to exchange heat with the hot streams and the cold streams are used to generate a higher quality utility. The rectangle area is proportional to the reduction of exergy loss.

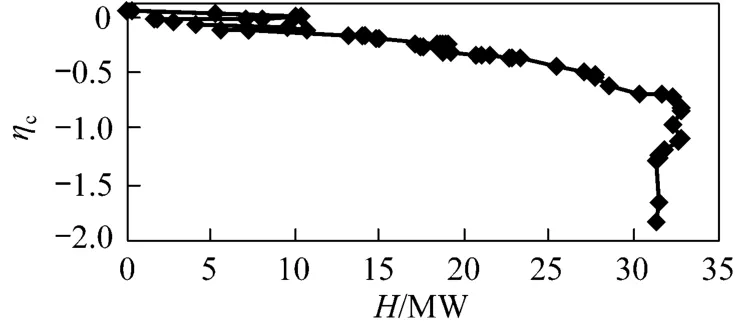
Figure 6 EGCC for the HEN of a chilling train in an ethylene plant

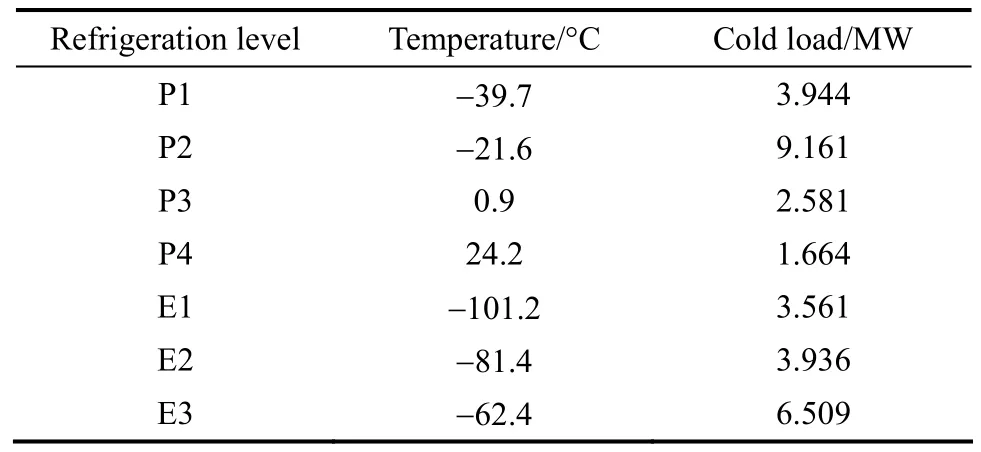
Table 2 The data of original cold utilities

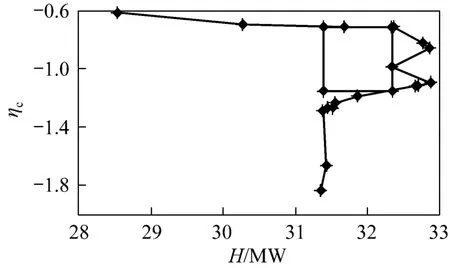
Figure 7 The pocket with the lowest temperature for the HEN of a chilling train

To maximum the area of the rectangle, a cold utility at −101.0 °C with 1 MW heat load is used to exchange heat with the hot streams in the pocket. Meanwhile, the process cold streams generate a high quality utility at −134.5 °C with 1 MW heat load. From the area of the rectangle, the reduction of exergy loss is 0.457 MW. According to Eq. (2), the reduction of the shaft work is 0.775 MW.

Next, the process without pockets is optimized. Fig. 8 is the EGCC. To find the optimum arrangement of cold utilities, which makes the area between the process streams and the utilities minimum, mathematical programming is used. The number of cold utilities is first set 7, then the levels of refrigeration are searched in the curve with the objective function of minimizing the area between the refrigeration and process streams. Table 3 shows the results with 7 optimum cold utilities. By calculating the area between the process streams and the cold utilities, we get the exergy loss of 2.316 MW. Then the reduction of exergy loss is 0.343 MW and the reduction of the shaft work is 0.581 MW.

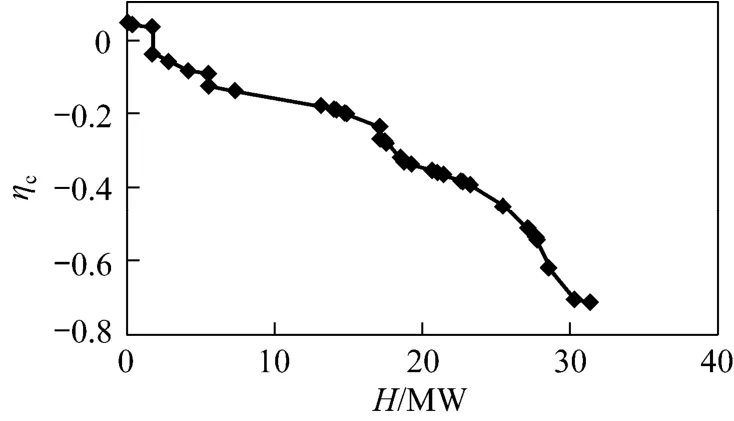
Figure 8 EGCC without pockets for the HEN of a chilling train in the ethylene plant

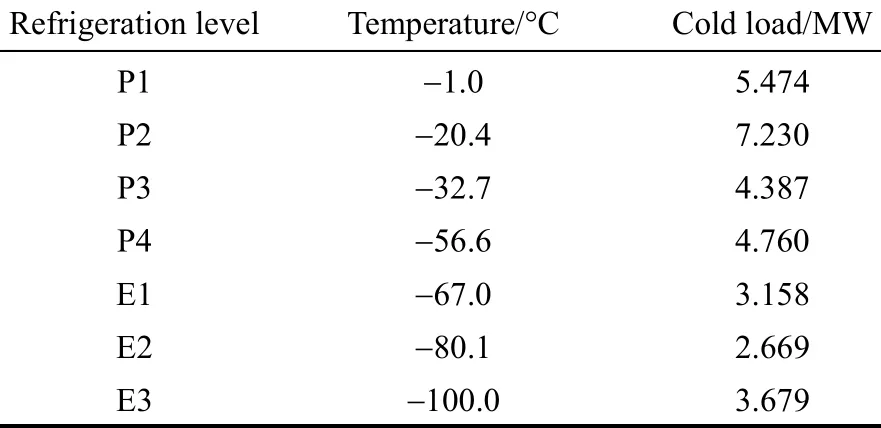
Table 3 The data with 7 cold utilities

Table 4 shows the optimum results with 8 cold utilities. The reduction of exergy loss is 0.454 MW and the reduction of the shaft work is 0.769 MW. Table 5 shows the optimum results with 6 cold utilities. The reduction of exergy loss is 0.140 MW and the reduction of the shaft work is 0.237 MW.

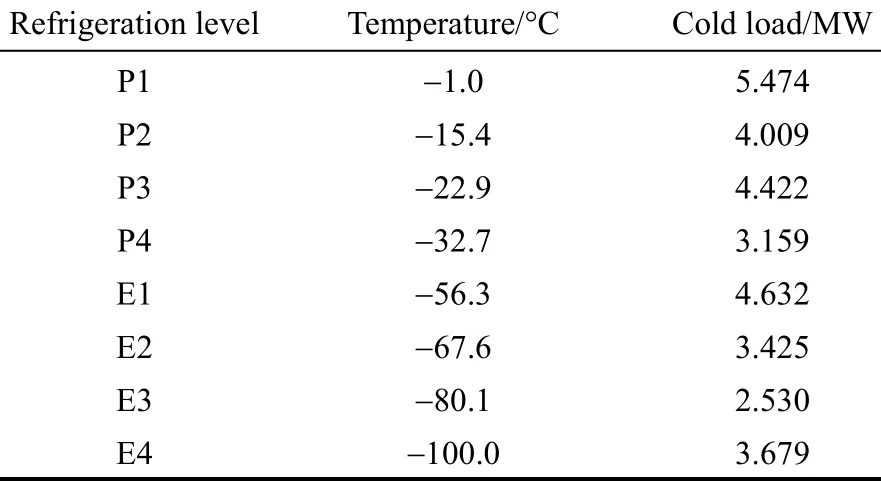
Table 4 The data with 8 cold utilities

Table 5 The data with 6 cold utilities

The results are compared in Table 6. The reduction of shaft work increases with the number of utilities, but the increment is reduced as the number is increased from 7 to 8. More utilities mean more capital cost, so a suitable level of utilities should be chosen by a trade-off between the reduction of shaft work and capital cost.

Table 6 Comparison of the reduction of shaft work with different numbers of utilities

4 CONCLUSIONS

This paper presents a two-step method to optimize HEN in a low-temperature process. The main purpose is to achieve the largest reduction of shaft work needed in HEN and to obtain optimal refrigerant levels. The cold pockets are first optimized to improve the energy performance of the system, which not only reduces the refrigerant quality requirement, but also generates higher quality refrigerant; then a mathematical method is used to find the best utility setting in the EGCC to cut down the cold pockets. The two-step method can give the optimal configuration of refrigeration levels in an efficient and effective way. A HEN of a chilling train with propylene and ethylene refrigerant cycle process is used as a case study. The results show that the two-step method can reduce the shaft work loss significantly.

NOMENCLATURE

Subscripts

REFERENCE

1 Linnhoff, B., Ashmad, S., “Super-targeting: Optimal synthesis of energy management systems”, Trans. ASME, J. Energy Resources Techno, 111 (3), 131-136 (1989).

2 Huang, K.F., Zhang, J.W., Feng, X., “Optimum setting for the utility system of ethylene plant”, Chemical Industry and Engineering Progress, 25, 466-469 (2006). (in Chinese)

3 Mehra Yuv, R., “Refrigeration charts for low temperature processes”, Chemical Engineering, 15 (1), 131-139 (1979).

4 Shelton, M.R., Grossmann, I.E., “Optimal synthesis of refrigeration systems”, Computers and Chemical Engineering, 10 (5), 461-477 (1986).

5 Linnhoff, B., “The pinch design method for heat exchanger networks”, Chemical Engineering Science, 38 (4), 745-763 (1983).

6 Linnhoff, B., Dhole, V. R., “Shaft work targets for low-temperature process design”, Chemical Engineering Science, 47 (8), 2081-2091 (1992).

7 Rosen, M.A., Dincer, I., “Exergy as the confluence of energy, environment and sustainable development”, International Journal of Eχergy, 1 (1), 3-13 (2001).

8 Linnhoff, B., “Pinch technology for the synthesis of optimal heat and power systems”, Trans ASME, J. Energy Resources Technol, 111 (3), 137-147 (1989).

9 Hui, C.W., Ahmad, S., “Total site heat integration using the utility system”, Computers and Chemical Engineering, 18 (8), 729-742 (1994).

10 Panjeshahi, M. H., Langeroudi, E.G., Tahouni, N., “Retrofit of ammonia plant for improving energy efficiency”, Energy, 33 (1), 46-64 (2008).

11 Umeda, T., “A thermodynamic approach to the synthesis of heat integration systems in chemical processes”, Computers and Chemical Engineering, 3 (1-4), 273-282 (1979).

12 Dhole, V. R., “Distillation column integration and overall design of sub-ambient plants”, Ph.D. Thesis, University of Manchester (UMIST), England (1991).

13 Wang, Y.F., Feng, X., Cai, Y., Zhu, M.B., Chu, K.H., “Improving a process’s efficiency by exploiting heat pockets in its heat exchange network”, Energy, 34 (11), 1925-1932 (2009).

14 Luo, Y.Q., Yuan, X.G., Liu, Y.J., “An improved PSO algorithm for solving non-convex NLP/MINLP problems with equality constraints”, Computers and Chemical Engineering, 31, 153-162 (2007).

15 Luo, Y.Q., Yuan, X.G., “Global optimization for the synthesis of integrated water systems with particle swarm optimization algorithm”, Chin. J. Chem. Eng., 16 (1), 11-15 (2008).

2013-08-13, accepted 2013-09-09.

* Supported by the National Basic Research Program of China (2010CB720500) and the National Natural Science Foundation (21176178).

** To whom correspondence should be addressed. E-mail: luoyq@tju.edu.cn