光学测量中光斑图像的处理及测量精度研究

周红锋，任朴生

(临沧师范高等专科学校 数理系，云南 临沧 677000)

在光学测量系统中，一般多用反射光线或汇聚光线形成的光斑进行测量，对采集到的光斑图像的处理直接影响到系统的测量准度、精度及其它指标。测量过程中，由于受被测物体表面倾斜、反射或散射特性变化及外界干扰等影响，使采集到的光斑图像信号的光强分布不均匀、畸变及光斑中心发生偏移。这就需要采用适当的图像处理技术对光斑进行必要的处理，以提高光斑图像区域的识别和定位精度，从而减小测量误差，提高系统的测量性能。本文以激光三角法测量小角度的实验系统为例，采用了几种常用的图像处理技术，对测量中的光斑图像进行分割和定位处理，并对其定位精度和测量结果进行了分析探讨。

1 实验系统简介

1.1基本原理。

该实验系统的测量原理[1]如图1所示，一束测量激光投射到待测平板上，当被测平板以O点为转轴转过一个微小角度α时，经物体表面反射的光线也会随之在CCD上发生移动。若令前后两次反射光线相交的夹角为β，则它们的几何关系为：

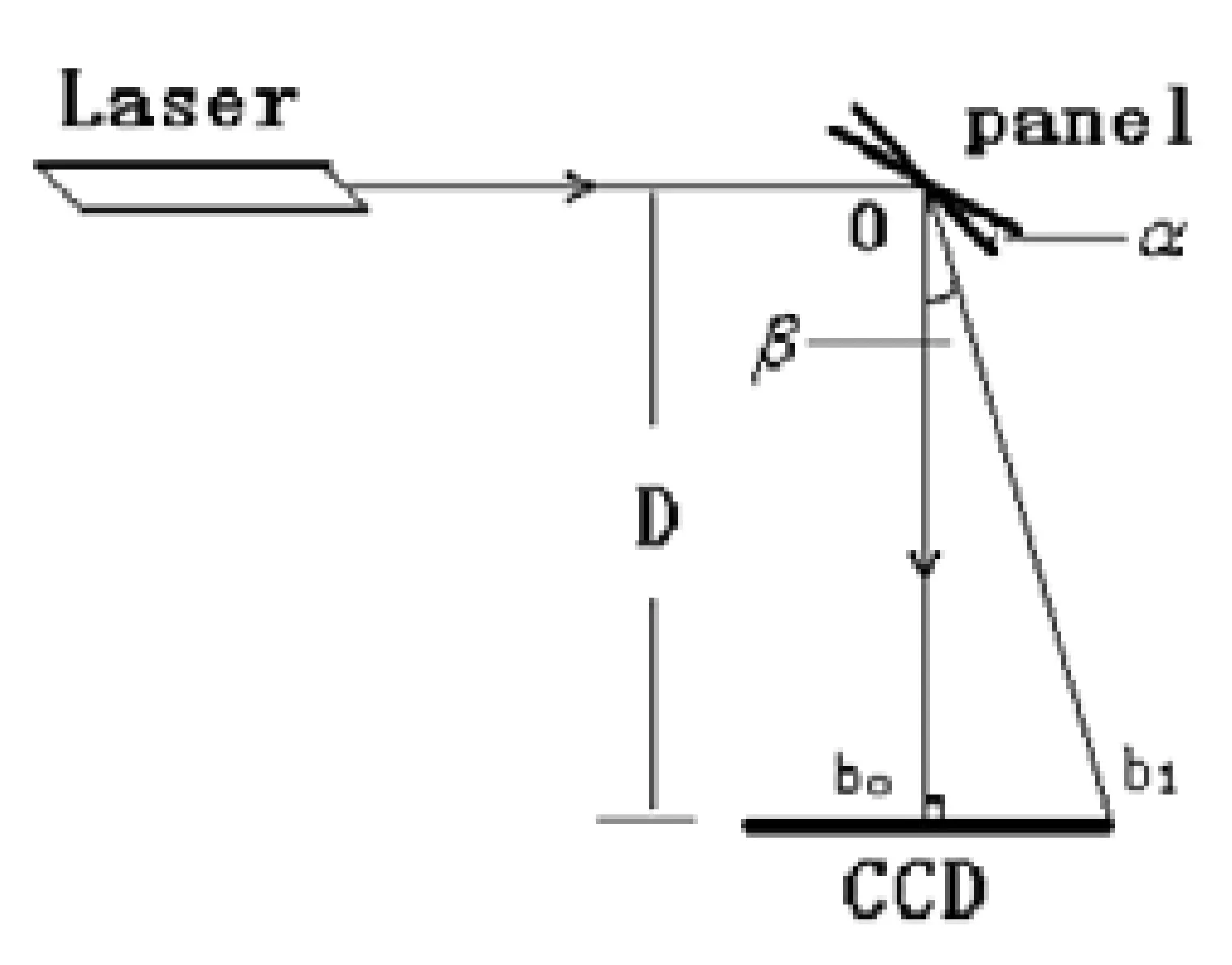
图1 实验原理图

β=2α

(1)

由图中的关系可得

(2)

(3)

测量时，只需计算出平板转动时激光的反射测量光斑在CCD上的位移(b1-b0)，再测量出平板转轴O到CCD的距离D，便可由(3)计算出此时平面板转过的角度α了。

1.2 实验系统及光路设计。[2]

该实验系统主要由防震台、He-Ne激光器、准直仪、待测平面镜及分光计、接收屏、CCD相机、图像采集卡和配套软件及装有图像处理软件的计算机组成，其实验的光路结构如图2所示。

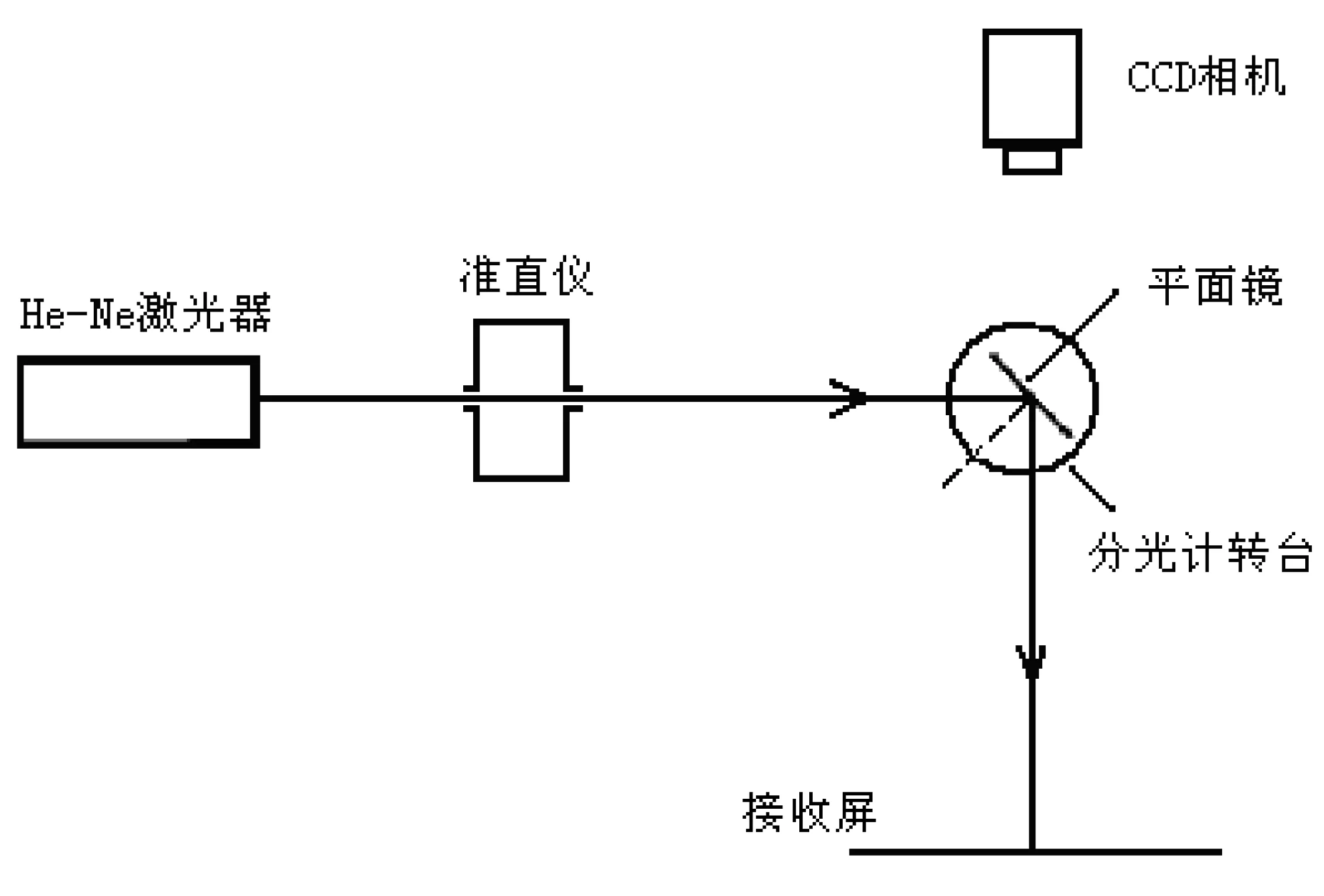
图2 测量光路结构图

在图2中，当平面镜转动一个微小角度时，接收屏上的测量光斑也随之移动。实验过程中，只需计算测量光斑在接收屏移动的距离，即式(3)中(b1-b0)的数值，便可算出此时平面镜在水平方向转过的微小角度。

2 光斑图像处理

2.1 光斑图像区域的分割。

在测量过程中，把光斑图像区域从背景中提取和分离出来，可以大大减小图像处理程序的开销、提高测量的速度，并且也提高了光斑图像区域中心位置坐标定位的精度和稳定性。由于光斑图像的光强度分布是典型的脉冲分布，图像中光强度值较大部分是光斑区域，而强度值较小部分则是背景。因此，只要选择合适的分割阈值，就可以把光斑区域从背景中分离出来。

分割的光斑区域 (b)迭代法分割的光斑区域

从图中可以直观地看出，迭代法能够更好的去掉杂散光斑点，其分割效果明显优于直接阈值法，当然其程序开销也比直接阈值法大得多。

2.2 光斑图像中心的定位。

在计算光斑图像区域的中心时，并不能简单地认为就是某个像素点，否则会带来较大的测量误差。为了精确计算分割得到的光斑图像区域的中心坐标，就必须应用适当的算法对其实施亚像素定位计算，[5]把对光斑图像区域的分辨和定位精度提高到比CCD象素尺寸更高的量级，从而大大提升实验系统的测量精度。实验过程中，采用形心法和灰度重心法来计算光斑图像区域的中心坐标，以实现其精确定位。

2.2.1形心法。

形心法是以图像的外形为特征，计算其几何中心，计算前需要把图像进行二值化处理。若二值图像I(i, j)中的目标区域为S，其形心(x0,y0)为：

(4-4-1)

(4-4-2)

由于图像中存在噪声，因此目标区域的二值化分割后将产生误差，目标边界会存在一些毛刺和断点，为了消除它对算法精度的影响，可对目标进行一些预处理，如形态学的扩张、侵蚀、开启和闭合等运算。

2.2.2灰度重心法。

灰度重心法可以看成是以图像灰度为权值的加权形心法。灰度图像I(i, j)中目标区域S的灰度重心(x0,y0)为：

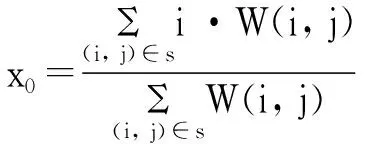
(4)

式中I(i, j)，为图像中坐标为(i, j)的像素的灰度值，W(i, j)为其加权值，计算中取W(i, j)=I(i, j)。

对于背景灰度值较小，而目标灰度值较高的情况，例如CCD测量中的光斑图、天文图像中的恒星，其目标的灰度分布多为抛物线或高斯曲面，具有基本对称的圆形分布，此时采用灰度重心法计算其中心位置，不仅算法相对简单，而且还能获得较高的测量精度。[6]

3 实验结果及分析

实验中，对计算机采集的同一测量过程中的6组光斑图像，经过几种不同图像处理技术处理后，把其中心坐标及对应转角的标准差进行了对照，如下表所示。表中只列出了光斑中心坐标值的平均值、中心坐标的标准差及对应被测转角的标准差；中心坐标及标准差保留到小数点后两位有效数字，转角的标准差保留到小数点后一位有效数字；σ形、σ灰分别表示采用形心法和灰度重心法处理时被测转角的标准差(中心坐标的单位为像素，转角的单位为秒)。

根据表中的数据可以看出，对原灰度图直接应用形心法和灰度重心法定位计算的中心坐标的标准偏差在0.7至0.9个像素左右，相应被测转角的标准偏差在8'' 左右；而经过两种分割算法处理后，其中心坐标和相应被测转角的标准偏差都逐渐减小。直接阈值法分割处理后，其中心坐标的标准偏差为0.6至0.7个像素左右，被测转角的标准偏差为6'' 左右；而采用迭代法分割处理后, 其中心坐标的标准偏差为0.5像素左右，被测转角的标准偏差为4'' 左右；其中心坐标和被测转角的测量精度都有了很大的提高，并且测量的稳定性也有了明显的改善。因而，在光学测量中应用适当的后续图像处理技术，能较好地提高测量系统的测量精度和稳定性。

[1]Daniel F. Garcia, Manuel Garcia, Faustino Obeso, Valentin Fernandez. Flatness Measurement System Based on a Nonlinear Optical Triangulation Technique. IEEE Transactions on Instrumentation and Measurement.2002,51(2):176-182.

[2]周红锋，王东云，等.激光三角法测量小角度的测量模型和光路设计研究[J]. 云南民族大学学报(自然科学版)，2008(3):277-279.

[3]K.R.Castleman. Digit Image Processing[M]. Prentice Hall, 1996: 186-213.

[4]钟志光,卢君,刘伟荣.Visual C++.NET 数字图象处理实例与解析[M].清华大学出版社,2003:371-372.

[5]于起峰，等.基于图像的精密测量与运动测量[M].科学出版社,2002:132-134.

[6]湛廷政,吕海宝.CCD细分技术方法研究及应用[J].光学学报,2002,22(11):1395-1399.