稳定性分析方法对均质土坡计算结果的影响

黄诗渊，刘健，徐静，曹智



稳定性分析方法对均质土坡计算结果的影响

黄诗渊1，刘健2，徐静1，曹智1

（1. 重庆交通大学 河海学院，重庆 400074；2. 重庆市水利电力建筑勘测设计研究院，重庆 470074）

以一均质土坡为例，分别采用瑞典法、毕肖普法、简布法等极限平衡法以及有限元强度折减法计算该土坡的稳定性. 研究了土条数目对条分法、网格密度对强度折减法的影响；并对这几种土坡稳定性分析方法的计算结果进行了对比分析，结果表明：极限平衡法和有限元强度折减法两类方法计算得到的安全系数和滑动面基本一致，极限平衡法得到的安全系数偏安全；各方法计算的模型划分得越精细，得到的安全系数越小，但随着精细程度的增加，安全系数减小的趋势趋缓.

土坡；稳定性；极限平衡法；强度折减法；安全系数

边坡工程的稳定性分析涉及道路、水利、铁路、建筑、矿山等众多工程领域，一直以来都是岩土工程研究中的热点和重点[1,2]. 研究边坡稳定性的目的是使工程边坡的结构合理化，或对危险边坡采取一系列的处理加固措施，防止发生边坡失稳，避免因滑坡等灾害带来人员和经济损失，因此，经济合理地设计边坡并对其进行稳定性分析评价显得尤为重要.

在边坡稳定性分析中，极限平衡法[3]应用得最为广泛，随着边坡工程计算理论以及计算机应用的不断发展，有限元强度折减法在边坡稳定性分析中的运用也得到了重视，许多学者对其进行了比较深入的研究与探讨，但是两类方法都存在一定的局限性，不同方法计算出来的结果也存在一定的差异. 本文在实际工程中分析对比这两类方法，其结果对于工程设计人员的实践有借鉴作用，对降低边坡灾害的发生概率具有一定的意义.

1 极限平衡法计算原理

极限平衡理论是最经典的确定性分析方法. 具体方法是将有滑动趋势范围内的边坡岩体或土体按规则沿着某一滑动面划分成若干竖条或斜条，通过块体的平衡条件建立整个边坡的平衡方程；以此为基础进行边坡分析，从而确定边坡稳定的安全系数. 该方法具有模型简单、计算公式简便、能够解决多种复杂的剖面形状、能够考虑各种加载形式等优点，在工程上应用广泛. 在过去的一百多年中，学者通过不同的假设，将极限平衡法分为瑞典法[4]、毕肖普法[5]、简布法[6]、摩根斯坦-普莱斯法、斯宾塞法、萨尔玛法等，其中常用的有瑞典法、毕肖普法、简布法.

1.1 瑞典法

瑞典法是一种不太严格的条分法，假定滑动面为圆弧形，滑动土体为不变形的刚体沿着圆弧面转动，而且假定土条两侧的侧向力大小相等、方向相反作用在同一直线上并相互抵消. 安全系数定义为每一土条在滑裂面上所能提供的抗滑力矩之和与外荷载和滑动土体在滑裂面上所产生的滑动力矩和之比，计算公式为：

1.2 毕肖普法

毕肖普法也是条分法的一种，它与瑞典法的不同之处是考虑了侧向力的不平衡，但计算过程中不考虑条块间的切向作用力. 假定各土体条底部滑动面具有相同的抗滑安全系数，该数值等于整个滑动面的平均安全系数. 因为考虑了土体的条间切向力，所以由毕肖普法所得安全系数的物理意义更加明确，结果相对来说更为合理. 此处采用考虑孔隙水压力的计算公式：

1.3 简布法

简布法是一种严格的条分法，它沿用了毕肖普法关于安全系数的定义和土条竖向应力平衡的公式，适用于任意形状的坡面，滑动面也可以是任意形状. 简布法不仅考虑了条间法向力的作用，还考虑了条间切向力的作用. 假定整个滑动面上的稳定安全系数是一样的，土条上所有竖向力合力的作用线和滑动面的作用点是同一点，已知推力线的位置，利用力矩平衡条件将条间切向力看成是条件法向力的函数，可求出滑动面的平均安全系数和应力分布，还能求出各个分界面上的抗剪安全系数以校对计算结果. 其计算公式为：

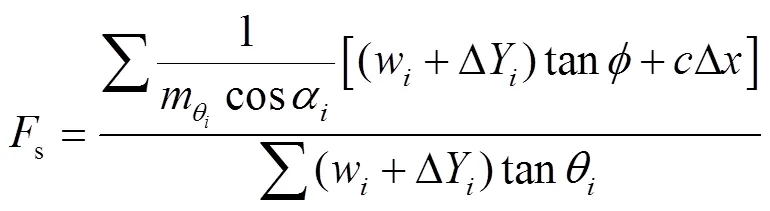
2 有限元强度折减法计算原理

有限元强度折减法[7-10]的基本原理类似于极限平衡法，故也叫做强度储备安全系数法. 相对于极限平衡法，有限元强度折减法克服了一些不足，它不需事先假设滑动面的形状（可以自动搜索需要的滑动面），也不需要假设条间力，考虑了土体的弹塑性本构关系并且满足应力—应变关系，能够模拟整个边坡的渐进破坏过程，同时反映边坡破坏失稳以及塑性区发展的过程.

在结果分析中，判断土坡失稳临界状态的标准有3种：1）以计算收敛与否为标准；2）以特征部位的位移拐点为标准；3)以是否形成一个连续的塑性贯通区为标准[11,12]. 本文采用第2种标准来判别边坡是否失稳.

3 算例分析

图1 模型简图

3.1 极限平衡法计算

采用岩土软件GEO-STUDIO中的SLOPE/W模块对该算例采用极限平衡法进行计算，计算时选取15种土条数目，计算结果见表1.

表1 极限平衡法计算结果

3.2 有限元强度折减法计算

图2 有限元强度折减法网格划分图（全局网格尺寸=1 m）

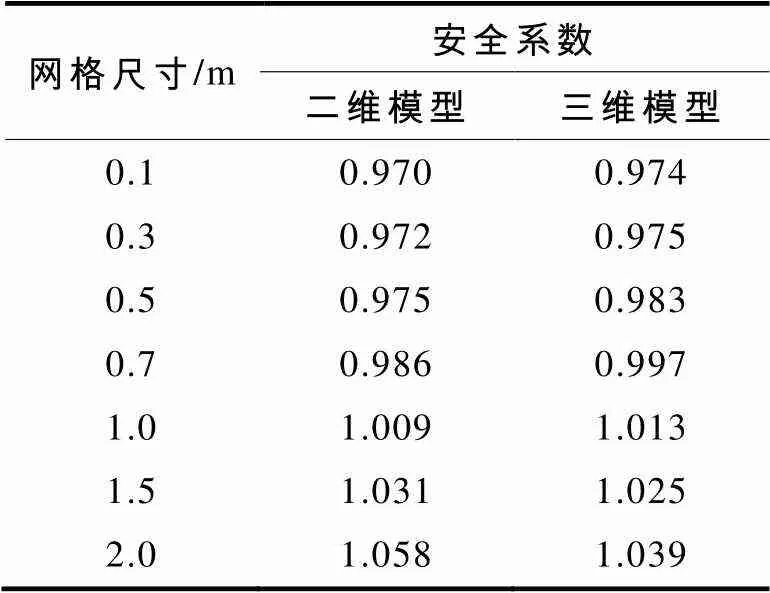
表2 有限元强度折减法计算结果

3.3 计算结果分析

3.3.1 安全系数

从表1和表2可知：1）3种极限平衡法计算的安全系数大致相同，大小顺序为毕肖普法＞瑞典法＞简布法，结果均相差在5%以内；2）有限元强度折减法的结果和3种极限平衡法的结果差别不大，总体上有限元强度折减法算得的安全系数略大些. 原因是极限平衡法假定边坡体是刚塑性的，没有考虑土体内部的应力—应变关系，而实际上土体在重力作用下形变时内部的应力有调整.

从图3可以发现，极限平衡法计算的安全系数整体上随土条数目的增多呈下降的趋势，在土条数目增多至30个以后，安全系数走势趋于平稳，说明在一定范围内，土条数目的增多可以增加计算的精确程度.

从图4可以观察到，有限元强度折减法计算的安全系数随着网格尺寸的减小而减小，说明网格尺寸越小，即网格密度越大，有限元强度折减法计算的安全系数越精确，但随着网格密度增加到一定程度，计算收敛困难，且精度增加不再明显.

图3 安全系数与土条数目关系图

图4 安全系数与网格尺寸关系图

图5 极限平衡法的滑动面（土条数目=15）

3.3.2 滑动面

比较图5与图6可以很清晰地观察到，有限元强度折减法和极限平衡法算出的滑动面的位置、形状基本一致，都是呈大致的圆弧状，且都通过坡脚点. 此外，在选取相同土条数目进行极限平衡计算时，滑动面顶点与坡顶点之间距离的大小顺序为毕肖普法＞瑞典法＞简布法；在同一种极限平衡法的情况下，滑动面顶点与坡顶点之间的距离随着土条数目的增多而减小.

图6 有限元强度折减法的滑动面（全局网格尺寸=1 m）

4 讨论

值得指出的是，本文的结论仅基于一个均质边坡的模型，未考虑影响边坡的尺寸、材料、形态等其他因素，因此，对边坡稳定性安全系数精度影响的研究还需要进一步的探讨.

[1] 刘立平，雷进生. 边坡稳定性分析方法的最新进展[J]. 重庆大学学报：自然科学版，2000, 23(3): 115-118.

[2] 刘金龙，陈陆望，王吉利. 边坡稳定性分析方法简述[J]. 水电能源科学，2008, 26(1): 133-137, 167.

[3] 曾亚武，田伟明. 边坡稳定性分析的有限元法与极限平衡法的结合[J]. 岩石力学与工程学报，2005, 24(A02): 5355-5359.

[4] 胡辉，姚磊华，董梅. 瑞典圆弧法和毕肖普法评价边坡稳定性的比较[J]. 路基工程，2007(6): 110-112.

[5] 戴自航，沈蒲生. 土坡稳定分析简化Bishop法的数值解[J]. 岩土力学，2002, 23(6): 760-764.

[6] 蔡志远，马石城，蔡志坚. 基于C语言程序的简布法边坡稳定性分析[J]. 长沙大学学报，2012, 26(5):20-22.

[7] 张鲁渝，郑颖人，赵尚毅，等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报，2003(1): 21-27.

[8] 宋雅坤，郑颖人，赵尚毅，等. 有限元强度折减法在三维边坡中的应用研究[J]. 地下空间与工程学报，2006, 2(5): 822-827.

[9] 郑颖人，赵尚毅，宋雅坤. 有限元强度折减法研究进展[J]. 后勤工程学院学报，2005, 21(3): 1-6.

[10] 马建勋，赖志生，蔡庆娥，等. 基于强度折减法的边坡稳定性三维有限元分析[J]. 岩石力学与工程学报，2004, 23(16): 2690-2693.

[11] 刘金龙，栾茂田，赵少飞，等. 关于强度折减有限元方法中边坡失稳判据的讨论[J]. 岩土力学，2005, 26(8): 1345-1348.

[12] 裴利剑，屈本宁，钱闪光. 有限元强度折减法边坡失稳判据的统一性[J]. 岩土力学，2010, 31(10): 3337-3341.

[责任编辑：熊玉涛]

Effects of the Stability Analysis Method on the Results of the Calculation of Homogeneous Soil

HUANGShi-yuan1, LIUJian2, XUJing1, CaoZhi1

(1. College of Hehai, Chongqing Jiaotong University, Chongqing 400074, China; 2. Chongqing Surveying and Design Institute of Water Resources, Electric Power and Architecture,Chongqing 470074, China)

This study takes a type of homogeneous soil slope as example, adopts the Fellenius method, the Bishop method, the Janbu method, and the finite element strength reduction method respectively to calculate the stability of the dirt slope, and then analyses the effects of the number of soilstripes on the slice method and the effects of the grid density on the strength reduction method. In addition, it makes a comparison of the calculation results of these methods for slope stability analysis. The results show that the safety factor and the slip surface of the limit equilibrium method and finite element strength subtraction method were basically the same, and the safety factor of the limit equilibrium method was stronger than that of the finite element strength reduction method; the finer the model partitioning is, the lesser the safety factor becomes; but with the increase of the partitioning density, the safety factor decrease trend levels off.

dirt slopes; stability analyses; the limit equilibrium method; the finite element strength reduction method; safety factors

1006-7302（2014）04-0043-06

TU457

A

2014-07-04

黄诗渊（1991—），男，江西赣州人，在读硕士生，主要从事水利、岩土方面的研究.