一道力学题的五种解法

徐姣芳 钟磊玖 丁敏方

（宁波市北仑中学 浙江 宁波 315800）

题目：如图1所示，一纸带放在水平面上，其上压一重物，现将纸带水平向右以恒定的速度匀速抽出，则：

A.重物质量越小，抽出纸带所用时间越短

B.重物质量越大，抽出纸带所用时间越短

C.重物与纸带间的动摩擦因数越小，抽出纸带所用时间越短

D.重物与纸带间的动摩擦因数越大，抽出纸带所用时间越短

图1

解法一：公式法

设重物质量为m，与木块间的动摩擦因素为μ，距纸带左边的距离为L，纸带速度为v.纸带对重物的滑动摩擦力f就是重物所受的合力，重物加速度

抽出时间应是与加速度相关，重物的加速度与质量无关，所以选项A，B错.

设纸带抽出所用时间为t，在这个过程中，纸带的位移

重物的位移

由几何关系（如图2）可得

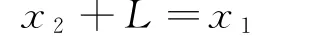
即

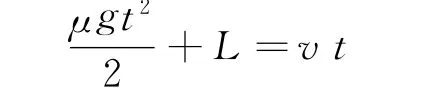
图2

公式变形得

纸带能抽出，方程（1）一定有解，其解为

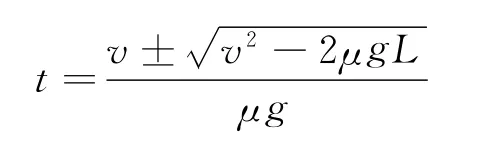
方程（1）的解，实际上是重物由静止开始以加速度μg加速运动，而纸带以速度v匀速运动，最终重物与纸带左端相遇的时间解.如果有两个解，则一个解是纸带抽出的时间t1，另一个解是纸带抽出后，重物继续做匀加速运动再追上纸带左端的时间t2，本题的解应为时间短的那个t1，则

在t的决定式中，没有重物质量因素，所以选项A，B错.

而且

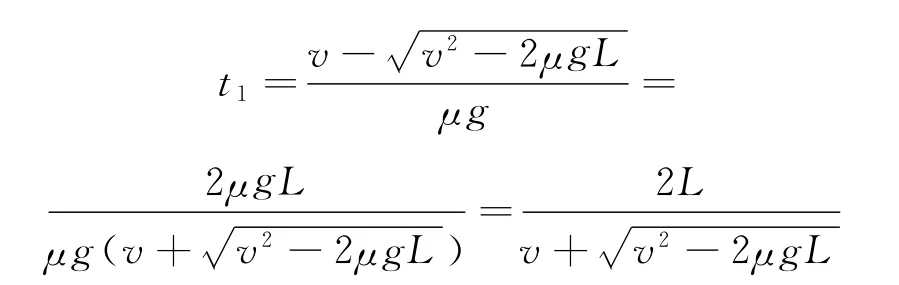
不难得出，μ越大，t也越大，C正确，D错误.

在下面的4种解法中，A，B的证明都与解法一相同.

解法二：v－t图像法

在抽出的过程中，纸带做匀速运动，重物以加速度a＝μg（解法一已经推导）做匀加速度运动，μ越大，a越大.作出纸带与重物的v－t图像（如图3），μ小的重物v－t图像对应斜线1，μ大的重物v－t图像对应斜线2.

图3

由几何关系可得，在抽出过程中纸带对地的位移与重物相对地的位移之差就是重物开始时距纸带左边的距离L，是确定的.反映到v－t图像上，就是：

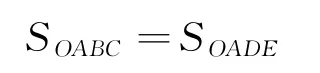
因此，t1＜t2，C正确，D错误.

解法三：定性分析法

在纸带抽取过程中，重物也在摩擦力作用下做加速运动，抽取时间决定于纸带相对于重物的速度，动摩擦因数大的，重物加速度大，速度增加快，任意时刻纸带相对于重物速度小，因此，抽取时间长，C对，D错.

解法四：特殊值法

不难理解，纸带抽出的时间与动摩擦因数μ有关，虽然本题没有给出具体数据，但可以自己假设便于计算的数据进行比较，例如，重物距纸带左边长度L＝1m，纸带抽取速度为v＝10m／s；

当μ1＝0.1时，由方程（1）可得

解出结果

当μ2＝0.6时，由方程（1）可得

解出结果

如果将μ1，μ2假设的数值差距大一些，便于比较.在此题中，比较t1，t2的大小，得t1＜t2，可得C正确，D错误.

需指出的是，撇开本题选项结构，仅凭上面两个数据就得出C正确是不严谨的，要加上“抽出时间随动摩擦因数是单调变化”的条件，才无懈可击.但本题已经证明A，B错了，C和D两个选项一定有一个正确，因此，根据这两个数据得出结论也是可以放心的.

本题用特殊值法还比较繁琐，但有些题采用这种方法判断是比较简单的.

解法五：极值法

极值法，实际上也是特殊值法，只是把特殊值取到最大或最小.

当μ取最小值零时，则在纸带抽出过程中，重物不动，时间的意义同解法一）.

当μ不等于零时，在纸带抽出过程中，重物都会跟着纸带向右运动一点时间，纸带相对地的位移要大于L，时间变长（μ取无穷大，重物瞬间就达到与纸带相同的速度，抽不出，或说抽取时间无穷大），C正确，D错误.

同样，“极值法”与“单调变化”联合才是严谨.但本题可以，原因解法四已述.

小结：通过对一道力学题多种解法的展示，目的在于启发学生开动脑筋，灵活运用不同的方法求解习题，激发学生的钻研学习兴趣，调动他们的发散思维，加强素质培养，提高学生分析问题和解决问题的能力.