数控系统可靠性测试试验数据的周期识别

高连生 高山峰

(①北京航空航天大学机械工程及自动化学院，北京100191;②北京航空航天大学机械工程及自动化学院CNC-SRT实验室，北京100191)

数控系统作为数控机床的重要组成部分，其可靠性直接关系到数控机床整机的可靠性水平［1］。对数控系统进行可靠性测试可以通过让其运行数控代码来实现。测试数控系统的运行状态获取其实际运行的试验数据是数控系统可靠性测试的重要内容。数控代码记录了数控加工的一切必要信息:工件的加工工艺顺序，运动轨迹与方位，工艺参数(转速、进给量和切削速度)以及辅助功能(换刀、变速和切削液开启等)［2］。数控系统的运行过程就是数控代码的执行过程。本可靠性试验采取无替换定时截尾的可靠性试验统计方案，即各个数控系统在无故障不需要停机的情况下一直在同一个NC程序的驱动下按照NC程序的周期运行。同时可靠性试验的数据采集系统也在马不停蹄地按照预定的采集周期采集数控系统的运行状态数据。因此随着试验的进行产生了大量的数据，而在对数据进行分析时，是盲目的。例如对于某一天某一时间段内的数据，并不知道这段时间内的数据与一个NC程序运行周期的关系，不知道该从何时开始对数据的分析才合适，所以在对数据进行分析时是盲目的。只有从大量数据中找到了某一个完整的运行周期的数据，以这个周期为参照进行数据分析才是合适的。所以期望按照数控系统所运行的数控程序的周期一个周期一个周期的对数据进行处理，所以很有必要对这些数据进行周期识别。数控系统是在数控程序的驱动下运行的，所以周期识别依照的肯定是其运行的数控程序。通过对数控程序进行解析，提取其中的主轴和各个伺服进给轴一个程序运行周期的运行状态来作为周期识别的参照，找到试验数据中的某个周期。找到了某个周期可以从这个周期开始对试验数据进行分析处理，可以得出每个周期中测试信号的特征。

周期识别其实就是通过建立合理的模型，然后提取一个周期的特征获得相应的特征参数的过程。石油大学的张来斌［3］等人在“柴油机缸盖周期性振动信号的自相关周期识别”中，利用拓展的周期信号自相关函数，实现了柴油机缸盖振动信号类周期的识别和主要振动波形的提取。沈阳航空工业学院的卢艳军［4］在“数控机床状态监测系统的研究”中，利用小波分析等信号处理技术和模式识别技术对数控机床的状态监测数据进行分析得出了监测信号的特征。中南大学的罗永顺［5］在“数控机床故障信号分析与特征提取”中使用Kalman滤波算法滤除了干扰振动信号;应用Laplace小波相关滤波法提取齿轮和轴承故障参数;并运用这两种滤波方法对机床主轴的振动信号进行滤波及故障特征的提取。因此在数控系统可靠性试验数据处理时可以借鉴相关信号处理技术和模式识别技术实现周期信号的自动识别。

1 周期信号的概念

一般周期信号定义为:对于信号x(n)，若有x(n+kN)=x(n)，k和N均为正整数，则称x(n)为周期信号［3］。即以一个时间间隔为周期，周而复始地出现性质相同的信号的现象。时间间隔称为周期，具有这种性质的信号称为周期信号。这一概念里，信号的性质相似有两点含义:①信号的时域指标相同;②信号的频域分布特性相同［3］。

2 数控系统可靠性试验数据的周期性

数控系统是由输入其内部的数控代码驱动来完成高速、高精度的加工的。数控系统的运行过程就是数控程序的执行过程。数控系统可靠性试验数据采集系统采集的是数控系统运行数控程序的结果。由于该可靠性试验选择了无替换定时截尾的统计方案，试验过程中数控系统始终在一个数控程序的驱动下运行，因此数控系统的运行结果是有周期性的，即数控程序的每一个运行周期为一个周期。例如主轴在两个运行循环的时域图形如图1所示。从图中也可以看出时域波形呈现一定的周期性。周期就是数控程序的运行周期。

3 数控系统可靠性试验数据的特征提取及周期识别

3.1 数控系统可靠性试验数据的特征提取

3.1.1 试验数据的特征表示

根据数控程序的解析结果可以得到数控程序一个运行周期各个测试信号的状态。在一段数控程序的运行过程中，用二进制数的0和1来分别表示主轴和各个伺服进给轴的旋转或位移状态，旋转的状态记为1，不转的状态记为0，同理，在某个方向上有位移的情况记为1，没位移记为0。利用速度位移公式可以得出主轴和各个进给轴一个程序周期的时域状态，例如图1所示。

可靠性试验采用1s的数据采集周期，即数据采集系统每隔1s采集一次测试信号的二进制状态1或0，因此采集的信号是一个一个离散的点。对于所采集的信号可以用数据结构SigItem来表示，该结构表示的信号状态是离散的。SigItem的结构为:

{

double time;//采集信号的时间点——时间间隔为采集周期(1 s)

int ncp;//NCPower信号的值

int ncr;//NCReady信号

int power;//24VPower信号

int spr;//主轴使能信号

intspon;//主轴旋转信号

intXon，Yon，Zon;//X，Y，Z轴的位移信号

……//其他信号

}

而在一个NC程序的运行周期中对于某个测试信号可以用如下的数据结构StatusAndTimeKept来表示其特征，用该结构表示的信号状态是连续的。Status-AndTimeKept的结构为:

{

intstatusValue;//信号状态值(1或0)

doublestartTime;//该状态的起始时间

double timeKept;//该状态的维持时间

}

3.1.2 试验数据的特征提取

可靠性试验采集的信号是离散的点，同时受采集系统性能、继电器性能或者数控系统本身插补性能及精度等各方面的影响，其中还可能存在干扰信号。

因此对于测试信号的特征提取就是对测试信号进行进一步的加工处理从大量的信号中寻找噪声，将噪声信号处理成合理的信号，在提高信号信噪比的同时根据信号状态的变化将离散的信号连续化并提取信号的特征参数。这里的特征参数就是前面所说的数据结构StatusAndTimeKept包括信号的状态、该状态的起始时间及维持该状态的时间长度。因此对于信号的特征提取可以分为3个步骤:(1)信号的连续化;(2)信号去噪;(3)信号特征提取。

(1)信号的连续化

在信号的处理过程中，可以根据信号状态的变化，将一个个离散的信号进行连续化，即将SigItem分别表示成StatusAndTimeKept结构，之后根据各个信号状态持续时间的长短来确定噪声。

信号的连续化首先开辟一个StatusAndTimeKept结构，然后对各个时间点的信号状态进行判断，如果下一个时间点的信号状态与上一个时间点的信号状态相同则只计入一次状态而把信号的持续时间累加，如果下一个时间点的信号状态与上一个时间点的信号状态不同，那么需要重新开辟一个StatusAndTimeKept结构，然后再重复进行上述判断直到指定的结束时间。这样，就把一个个离散的时间点信号连续化了。

(2)信号去噪

在对测试信号进行分析后，可以得出对于噪声信号可定义为夹杂在合理信号中的持续时间很短的信号，并且该段信号两端的信号状态应该是相同的。至于短到什么程度，需要给出一个适当的比例(信噪比)。对于信号的降噪，首先要确定信号的噪声，然后才能根据信号的变化过程，对其进行处理。在上面已经进行了信号的连续化，那么对于信号噪声的寻找就简单了。例如图2的信号状态变化过程表示成Status-AndTimeKept的结构为:

(1，0.0，200.0)，(0，200.0，160.0)，(1，360.0，10.0)，(0，370.0，180.0)，(1，550.0，200.0)，(0，750.0，15.0)，(1，765.0，160.0)，(0，925.0，40.0)

把该结构的第3个参数:信号状态的维持时间与给定的去噪标准进行比较，如果某一时间段小于这个标准，并且该段信号前后的信号的状态相同且维持时间较长，就认为该处信号是一个噪声，然后再根据该信号前后信号的状态将该信号处理成合理的状态。例如上述信号变化过程，假设去噪时的信号维持时间标准为20 s，那么在逐步比较中可以得出第3个时间段10.0 s和第6个15.0 s都小于去噪标准，并且与前后较长时间段的信号状态相反，则判定这两处为噪声信号。找到噪声信号后，根据噪声前后信号的状态，将噪声信号的状态改为与其状态相同的信号，将噪声信号的持续时间以及它后面信号的持续时间分别都累加到噪声信号前面的信号维持时间上，以此类推，然后再表示成原来的数据结构。图2信号去噪后如图3所示。表示成StatusAndTimeKept的结构为:

(1，0.0，200.0)，(0，200.0，350.0)，(1，550.0，375.0)，(0，925.0，40.0)

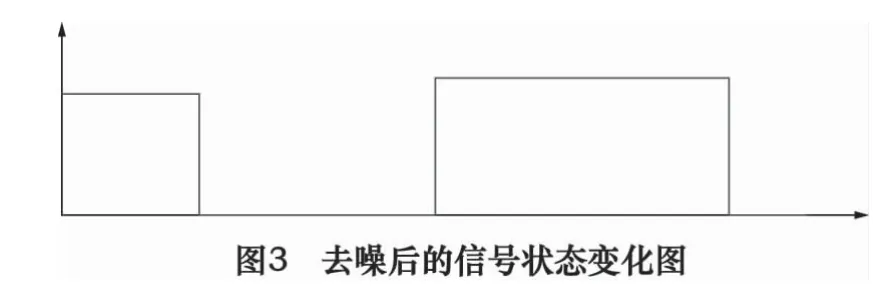
(3)信号特征提取

信号的特征提取就是将信号连续化及去噪后的结果累加，表示成前面所说的连续的StatusAndTimeKept的数据结构，然后提取它的特征参数。

3.2 周期识别

因为试验数据的周期性是靠数控程序运行的周期性来保证的，因此试验数据的周期识别需要以数控程序对测试信号的解析结果作为基准来完成。所以，为了以数控程序的解析结果作为基准去识别试验数据的周期，在对试验数据进行降噪的同时需要对数控程序的解析结果进行相同标准的去噪处理，并将其结果表示成与Status And Time Kept结构类似的Standard Status And Time Kept结构，然后再以去噪后的数控程序的周期为标准去在大量的试验数据中寻找试验数据的周期。

StandardStatusAndTimeKept的结构为

{

intstatusValue;//信号状态值(1或0)

double timeGap;//该状态的维持时间

}

StatusAndTimeKept结构中保留状态起始时间StartTime这个属性是为了以后寻找故障时间。

周期识别就是将标准的StandardStatusAndTimeKept信号数据作为基准在大量的试验数据StatusAnd-TimeKept中寻找与该结构各个参数值相差在一定误差范围内，并且各参数的顺序与标准顺序一致的一个周期。例如，图4a表示某信号一个周期的变化情况，图4b是随机地从大量试验数据中截取的该信号的测试结果。从图4中可以看出试验数据与标准程序运行周期的关系。图4b中的部分才是大量试验数据中的一个标准的周期。该部分前面和后面分别是另外的周期。所以在周期识别中不仅要考察信号的状态是否与标准周期一致，同时要考察信号的持续时间与标准周期的接近程度，还需要考察这两个参数为整体构成的结构与标准周期信号结构之间的先后顺序才能找到正确的周期。

周期识别算法的具体思路是:首先进行信号状态的匹配检查:对试验信号的状态与标准信号的状态进行匹配，如果两信号状态相同接着进行信号持续时间的误差匹配检查，如果持续时间在误差范围内，把信号状态和信号状态持续时间作为一个整体，考察信号状态变化的顺序性，直到最后返回一个周期起点的下标位置。

4 结语

试验数据是可靠性试验最宝贵的资源。随着试验的进行，试验数据是逐步累加并且有周期性的。然而由于该课题的性质，导致对于任意时间段内的数据却无法确定其与周期的关系。本文从数控系统所运行的数控程序的周期性入手来对大量的试验数据进行周期识别，给出了相关算法的思想，该方法有利于实现数据处理的智能和自动化。试验数据周期识别的实现为进一步分析数控系统的各个测试信号以及数控系统运行故障奠定了基础。

［1］韩兴国.数控机床运行状态数据采集及数据处理技术研究［J］.装备制造技术，2012(6):245-247.

［2］胡荣强，苏义鑫.数控机床NC代码的解释与执行［J］.计算机应用研究，1996(2):79-80.

［3］张来斌，潘兴德等.柴油机缸盖周期性振动信号的自相关周期识别［J］.石油大学学报:自然科学版，1999，23(6):57-58，72.

［4］卢艳军.数控机床状态监测系统的研究［J］.制造业自动化，2008，30(8):34-36.

［5］罗永顺.数控机床故障信号分析与特征提取［D］.长沙:中南大学，2007.