关于偏相关系数的计算公式的一点注记

陈敏琼，彭东海

1 偏相关系数常见的几种定义与计算方法

定义1［1］设变量组 ｛X1，X2，…，Xp｝之间存在线性关系：

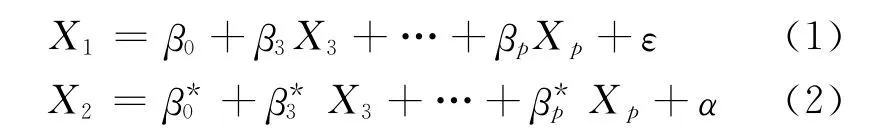
其中ε，α为随机扰动项，则在X3，…，Xp给定的条件下X1与X2的偏相关系数的大小可定义为：

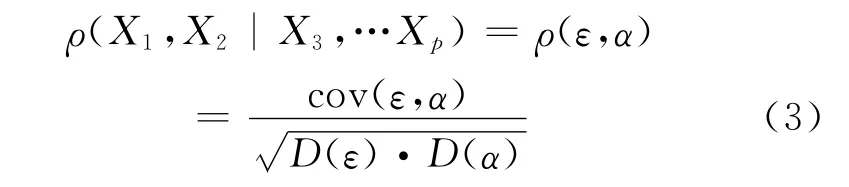
若有样本数据则可通过样本数估计得出模型（1）和（2）的残差序列｛i｝，｛｝，i＝1，2，…，n，则X3，…，Xp给定的条件下X1与X2的样本偏相关系数为：

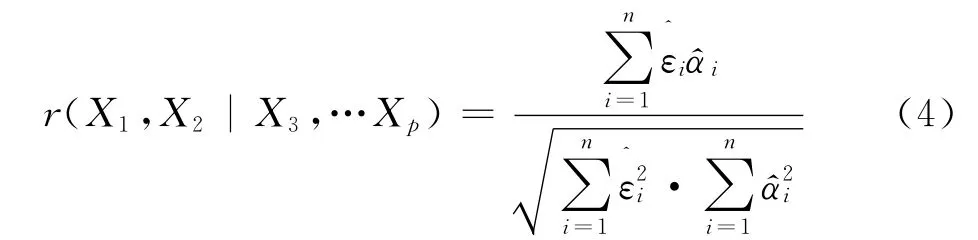
定义2［2］设回归模型

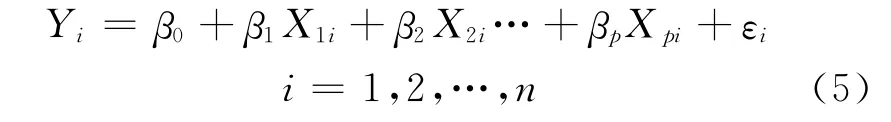
记Y的 残 差 平 方 和 为SE（X1，X2，…，Xp），而SE（X2，…，Xp）表示去掉变量X1后建立的新的回归模型

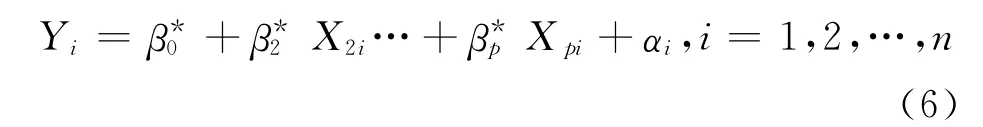
的残差平方和，则称

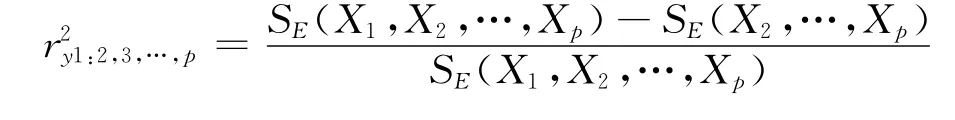
为变量Y关于变量X1的偏决定系数。而称此偏决定系数的平方根

为Y与变量X1的偏相关系数。

公式3［3］设有变量组｛X1，X2，…，Xp｝，其相关系数阵为

其中，rij表示变量Xi，Xj的简单相关系数.则 ∀i，j＝1，2，…，p，变量Xi与Xj在其他变量给定的条件下的偏相关系数为：

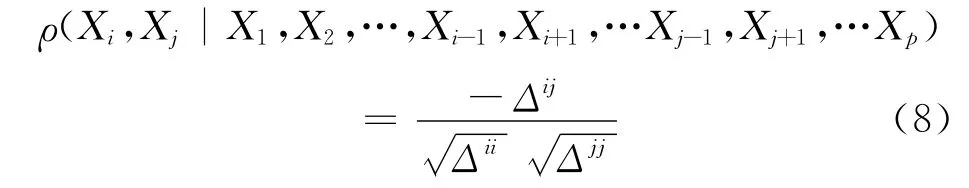
其中，Δij，Δii，Δjj分别为｜R｜中元素rij，rii，rjj的代数余子式。

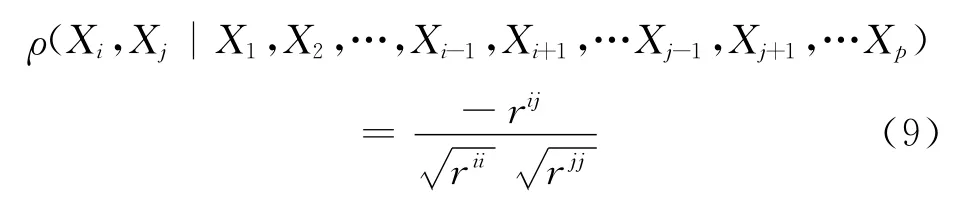
定义1所给出的偏相关系数的定义侧重说明两变量在扣除其他变量的影响之后的“纯相关”，定义2所给出的偏相关系数的定义则常在回归分析中用来衡量某个自变量对因变量的重要性，以判定该自变量是否需要加入模型中（事实上可以证明定义2的计算公式就是定义1所定义的偏相关系数的绝对值）。定义1与定义2都是基于回归分析提出的，笔者以为回归分析的前提条件是已明确变量之间是具有因果关系的，这样定义出来的偏相关系数不具有对称性，也不符合相关分析的本质。而公式3给出的计算公式则没有区分变量之间的因果关系，因而更合理，而且计算上也简便。下面笔者将通过分析得出公式3所指出的两变量之间的偏相关系数计算公式，事实上是基于多元正态分布理论中的条件分布的结论导出的。

2 偏相关系数的计算公式（9）的理论依据——基于多元正态分布理论

由此条件协方差阵可计算在X（2）给定的条件下，X（1）中两两指标之间的偏相关系数大小。

故在X3给定的条件下X1与X2的偏相关系数的大小为：

其中，ρij表示变量Xi与Xj的简单相关系数大小，i，j＝1，2，3。

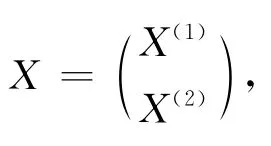
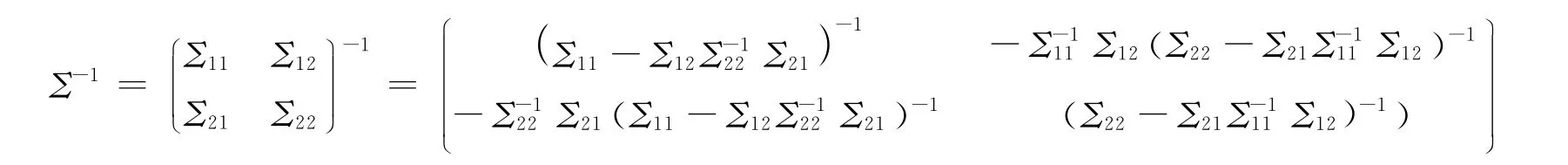
此结论说明在X3，…，Xp给定的条件下X1与X2的偏相关系数的大小

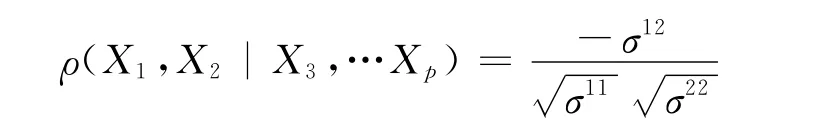
其中σ11，σ12，σ22分别为协方差阵Σ的逆矩阵Σ－1中的第1行第1列的元素、第1行第2列的元素及第2行第2列的元素。

类似，若要求变量Xi与Xj（不妨设j＞i）在其 他 变 量X1，X2，…，Xi－1，Xi＋1，…，Xj－1，Xj＋1，…Xp给定的条件下的偏相关系数，可令

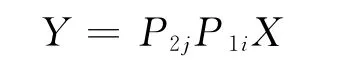
（其中P1i表示单位阵Ip的第1行与第i行交换所得的初等阵，P2j表示单位Ip的第2行与第j行交换所得的初等阵）。则由多元正态分布性质可知

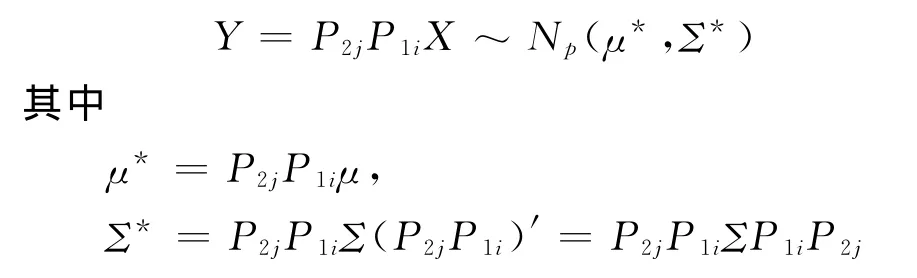
由前面推导结论可知Xi与Xj（注：此时Xi与Xj为向量Y的第一和第二个指标）在变量X1，X2，…，Xi－1，Xi＋1，…，Xj－1，Xj＋1，…，Xp给定的条件下的偏相关系数

其中，c11，c12，c22分别为Y的协方差阵Σ＊的逆矩阵（Σ＊）－1中的第1行第1列的元素、第1行第2列的元素及第2行第2列的元素。

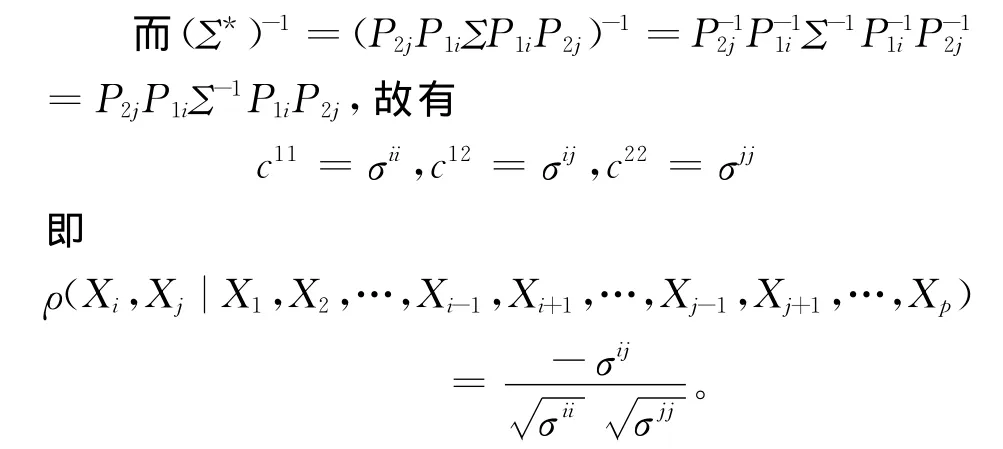
综合上述可知，若随机向量X＝（X1，X2，…，Xp）′～Np（μ，Σ），Σ＞o，记Σ＝ （σmn）p×p，其中σmn＝cov（Xm，Xn），m，n＝ 1，2，…，p，且记Σ－1＝（σmn）p×p，则在其他变量X1，X2，…，Xi－1，Xi＋1，…，Xj－1，Xj＋1，…，Xp给定的条件下Xi与Xj的偏相关系数大小为：

另外，由随机向量X的相关系数阵R与协方差阵Σ的关系：

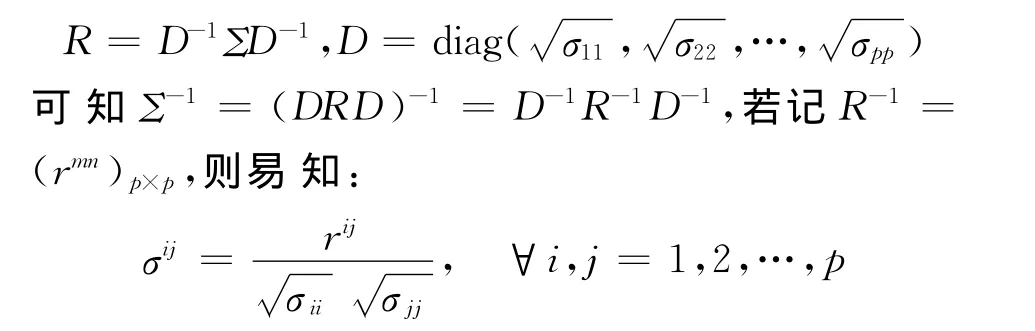
从而可得：

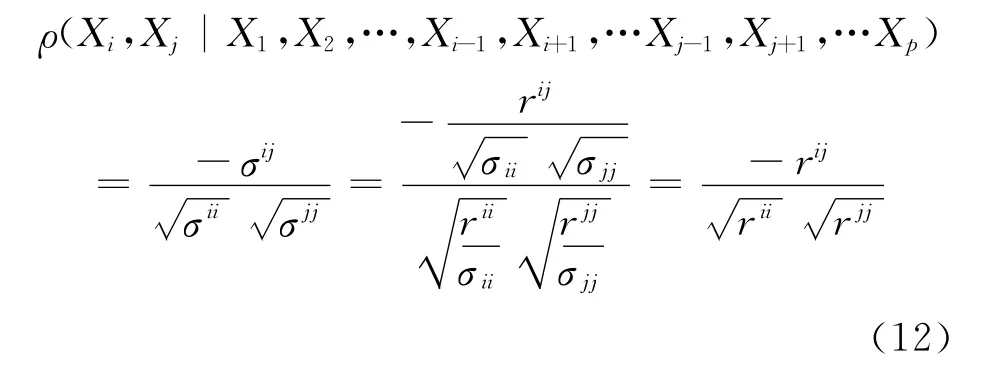
至此，公式（9）得证。

3 结论

本文从多元正态分布理论中的条件分布的结论出发，论证了公式3所提出的两变量之间的偏相关系数的计算公式（9）的合理性。该结论说明对于联合分布服从多元正态分布的向量组｛X1，X2，…，Xp｝来说，若要求变量组中两两变量之间的偏相关系数（即“净相关”）大小，只需知道该向量组的协方差阵Σ或简单相关系数阵R（未知时可通过样本进行估计），通过求Σ－1或R－1，再按（11）式或（12）式计算即可（若变量只有3个，则更简单，按（10）式计算即可）。因此计算方便且定义合理。但注意前提条件是变量组的联合分布必须服从多元正态分布，至于如何验证联合分布是否服从多元正态分布则不是本文讨论的重点。

［1］李 钢.关于偏相关系数计算思想的思考［J］.商场现代代，2008，（中旬刊）：388－389.

［2］王黎明，陈 颖，杨 楠.应用回归分析［M］.上海：复旦大学出版社，2008：65－66.

［3］郝黎仁，樊 元，郝 欧.SPSS实用统计分析［M］.北京：中国水利水电出版社，2007：184.

［4］何晓群.多元统计分析（第二版）［M］.北京：中国人民大学出版社，2010：12－15.