对易变质多物品库存系统的最优订购策略的探究

童 伟，姚云飞

随着物流业的快速发展，库存控制与管理逐渐受到重视，经典的EOQ模型也越来越广为熟知。但是EOQ模型由于其参数固定而具有一定的局限性。在实际生活中，许多物品具有一定的变质性，例如血液、酒精、水果等食品。覃毅延［1］等提出了需求随价格变化的具有折扣的易变质物品的库存模型，证明了当供应商给予数量折扣时，零售商的需求量是增大的，并给出了供应商给予数量折扣时零售商的订货量和订货周期的计算方法。励凌峰［2］等研究了变质率服从 Weibull分布的易变质物品的最优采购和库存策。王道平［3］建立了在需求和采购价格均为时变的易变质物品EOQ模型.罗兵［4］等进一步考虑了变质物品在存货影响销售率且需求和采购价均为时变时的EOQ模型。

近年来多物品库存受到越来越多的关注。Bhattacharya［5］考虑了需求为线性的情况下两种易变质物品的库存问题。Saha［6］建立了需求依赖库存水平的易碎多物品库存模型。莫降涛［7］等给出了易变质多物品最优订购策略的线搜索算法。

本文所研究的是易变质多物品库存系统的最优订购策略，采用适当的订购策略，使得库存系统单位成本最小。一般的订购策略有两种：一是一次性订购所有的物品，也就是每一次订购，则所有的物品都订购，这种策略比较方便，但缺乏一定的变通性；二是部分物品同时订购，将一些订购频率差不多的物品同时订购。这种方法考虑到物品的组合，每次订购可以选择性的订购部分物品。本文给出第一种策略的最优解，第二种策略的估计解，并用数值例子对两种策略进行比较。

1 模型符号说明与假设条件

（1）n表示库存系统订购的物品种类数量，ni表示第i种物品，i＝1，2，…，n

（2）Di为第i种物品的需求率，为常数。

（3）不允许缺货，补货率无限大，提前期为零。

（4）A为一次订购物品的基本订购费。

（5）Ai为订购第i种物品额外的订购费，ci为第i种物品单位购买成本，h为单位物品单位时间库存持有成本占单位购买成本的百分比，T为库存周期长度。

（6）αi为第i种物品的变质率，Ii（t）为第i种物品在t时刻的库存水平。

2 模型建立与解的分析

2.1 考虑第一种订购策略，即一次订购所有物品

在这种情况下，所有物品有共同的订购周期，则第i种物品在t时刻的库存水平满足下式

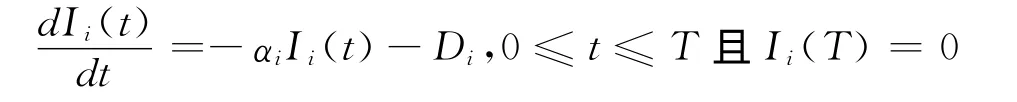
解上述微分方程，得

相应的得到第i种物品的库存费为：

变质费为：

库存系统在一个周期内的平均成本为：

事 实上可令f（x）＝ex［（x－1）2＋1］－2，则

当x＞0时f′（x）＞0，所以f（x）在（0，＋∞）上是严格增函数。

定理1atc（T）有最小值解，且唯一。

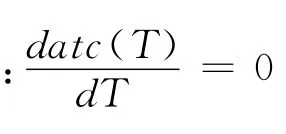
2.2 部分产品同时订购

2.2.1 模型的建立

这种情况下，我们考虑订购最为频繁的一种物品，令这种物品的订购周期为T，则其余物品的订购周期为T的mi（mi为正整数）倍，第i种物品的订购周期即为miT，则第i种物品在t时刻的库存水平满足下式

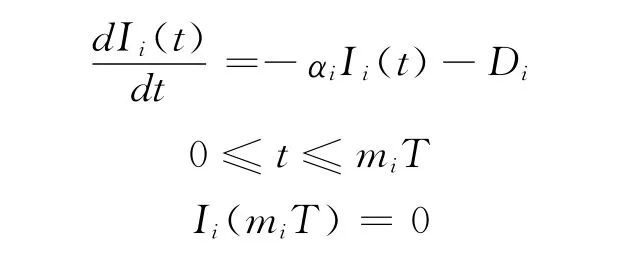
解上述微分方程，得

相应的得到第i种物品的库存费为：

变质费为：

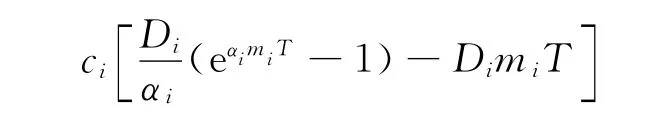
库存系统在一个周期内的平均成本为：

为方便，以下将ATC（T，m1，m2…mn）简记为ATC。若ATC要取得极值需满足下式：

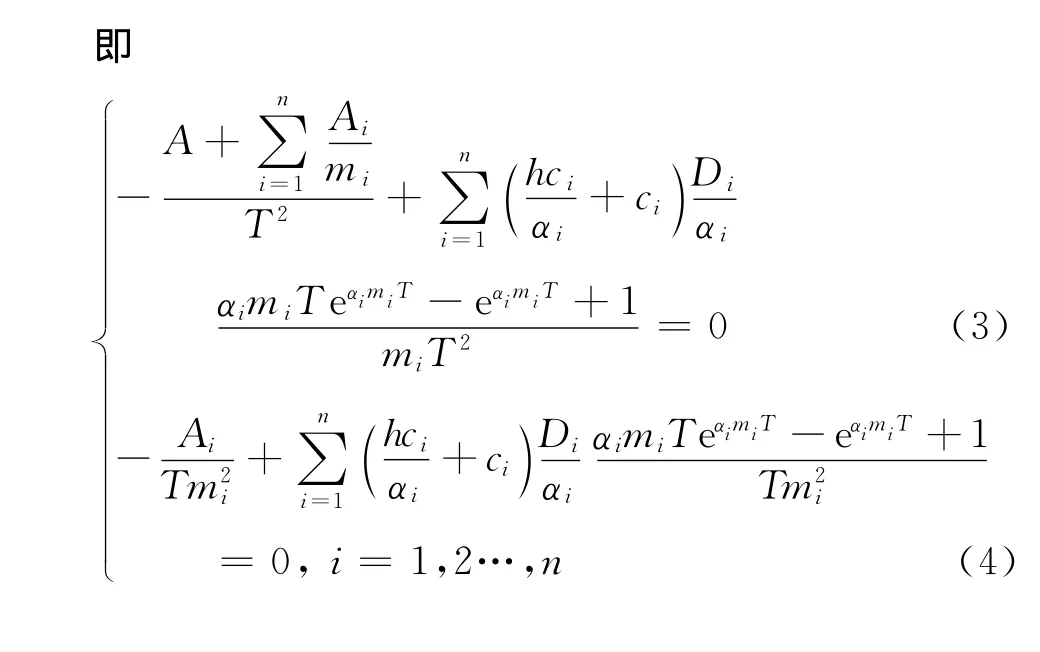
定理2 若存在满足（3）式和（4）式的一组解（T＊，m＊1，m＊2…m＊n），则该解是ATC的最小值解。

证明 分别用ATC对T和mi求二阶偏导，可得：

将（3）式带入上式化简可得

其n＋1个顺序主子式为

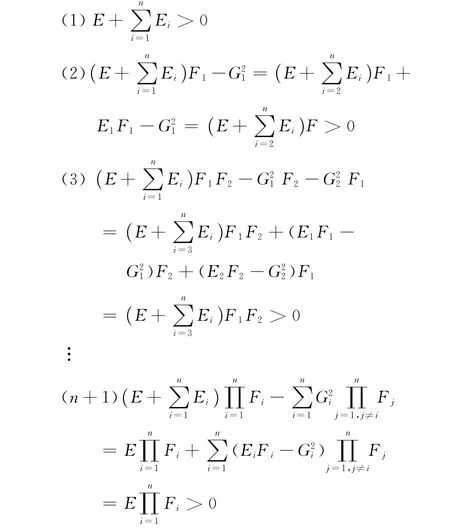
定理3 对于给定的一组值 （m1，m2…mn）（mi＞0）（4）式有唯一确定的解T；对于给定的T（T＞0），（4）式有唯一确定的一组值 （m1，m2…mn）。

证明 将（3）式左右两边同时乘以T2，然后

令左边为M（T），则

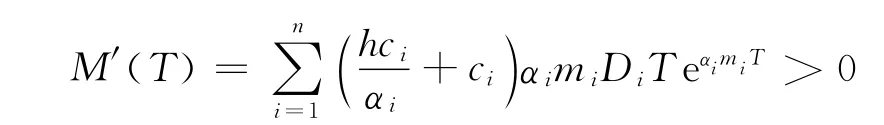
则M（T）在（0，∞）上是严格增函数

当T→＋∞ 时，M（T）→＋∞，由介值定理可知，M（T）存在唯一确定的解T，该解T也即为（3）式的解。

同理，将（4）式左右两边同时乘以Tm2i，然后令左边为Ni（mi）（i＝1，2…，n），则

则Ni（mi）在（0，∞）上是严格增函数Ni（mi＝0）＝－Ai＜0，当mi→＋∞时，Ni（mi）→＋∞，由介值定理可知，M（T）存在唯一确定的解mi，该解mi也即为（4）式的解。证毕。

对于（3）式和（4）式的解很难求解出，但是由定理3我们知道对于给定的一组值（m1，m2…mn）（mi＞0）（3）式有唯一确定的解，所以，若能给出 （m1，m2…mn）的估计值，则最优解T很容易求出，从而得到较好的库存系统平均费用的值。

2.2.2 模型的求解

首先由

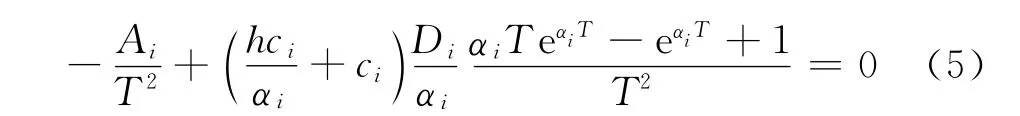
算出每一个物品单独订购的最优周期，令其中最优周期最小的物品i的mi＝1，则其他物品的mj由下式给出

这种方法能很好的体现出不同变质率下物品的订购频率，因此是个比较不错的估计方法。

综上所述，对于策略2，我们可以给出算法如下：

Step 1：输入各参数，求解方程（4），得到Ti，令Ti值最小的物品mi＝1

Step 2：由（5）式 求解出mj，且令mj取整到最接近的整数

Step 3：将所有物品的mi值及各参数带入（3）式并计算出T＊

Step 4：用（2）式计算出平均成本ATC

3 实例

某超市订购4种物品，其各参数如表1.其中h＝0.2，A＝100。

表1

利用本文所给出的算法，得到T1＝0.32，T2＝0.4575，T3＝0.434，T4＝0.248。所以选物品4的m4＝1，则m1＝1，m2＝2，m3＝2，T＊＝0.2917，ATC（T＊）＝2967.61，Q＊1＝117，Q＊2＝478，Q＊3＝829，Q＊4＝592。

若将各参数值带入（1），解得若使用策略1，其最优T＊＝0.3491，atc（T＊）＝3259.75。由此可以看出策略2被策略1更好。

下面分析物品的变质率αi对库存系统最优订购策略的影响，为方便起见，这里只以物品1为例。

表2

从表中可以看出，随着变质率的增大，库存系统的最优订购周期逐渐减少，而平均成本增加。

4 结束语

本文对易变质多物品库存系统提出了两种订购策略，以系统平均费用最少为目的建立模型，并尝试着给出其最优解。最后通过数值列子比较两种策略的优劣，并对物品变质率对系统订购周期和平均成本进行了数值分析。本文的研究中还有些不足，没有考虑购买费用滞后支付对库存系统的影响，如果允许滞后支付该如何制定最优订购策略，这些问题值得进一步研究。

［1］励凌峰，黄培清，骆建文.易腐物品的库存管理研究［J］.系统工程，2004（123）：25－30.

［2］覃毅延，唐焕文，郭崇慧.需求随价格变化的具有折扣的易变质物品的库存模型［J］.运筹与管理，2006，15（4）：22－26.

［3］王道平，于俊娣，李向阳.需求和采购价格均为时变的易变质物品EOQ模型［J］.数学的时间与认识，2011，41（8）：59－66.

［4］罗 兵，杨 帅，李宇雨.变质物品在存货影响销售率且需求和采购价均为时变时的EOQ模型［J］.工业工程与管理，2005（3）：40－44.

［5］Bhattacharya.D.K.Production，manufacturing and logistics on multi－item inventory［J］.European Journal of Operational Research2005，162（3）：786－791.

［6］Saha A ，et al.Inventory models for breakable items with stock dependent demand and imprecise constraints［J］.Mathematical and computer Modeling，2010（52）：1771－1782.

［7］莫降涛，陈桂梅，范婷，毛宏.需求依赖即时库存水平的易变质多物品最优订购［J］.系统工程，2011（209）：98－102.