基于改进TOPSIS法的航空发动机性能评估方法

黄燕晓

（中国民航大学 职业技术学院，天津 300300）

0 引言

准确评估航空发动机性能是发动机健康管理的关键，也是确保其安全的措施之一。近年来，多参数评估方法以有效性和实用性广泛应用于航空发动机性能评估领域[1]。国内外学者和研究人员进行了广泛研究，其中杨皓翔等采[2]用AHP法和熵值法组合确定权重以及采用“Kullback leibler距离”代替“欧氏距离”计算贴合度来评估地下水水质的优劣；肖淳、邵东国[3]等采用“垂直距离”代替“欧式距离”来衡量方案逼近理想解程度的正交投影法与常规逼近理想解技术相结合的TOPSIS改进方法建立流域初始水权分配模型；Karimi, M, Moztarzadeh, F, Pakzad, A.等[4]在金融风险管理方面应用模糊的TOPSIS法进行评估。

但是上述研究在利用TOPSIS法时都忽略TOPSIS法存在的不足，也未考虑各参数间的相关性从而使得决策信息在计算时重复计算，导致计算精度不高。为解决这一问题，本文采取措施改进TOPSIS法，并利用ANP法在计算各参数权重时考虑参数间相关度，以增加发动机性能评估的准确度。

1 发动机性能评估TOPSIS法及不足

TOPSIS[3]方法，首先构建机队中发动机性能决策矩阵并进行规范化处理，确定机队中发动机性能的正理想解和负理想解，然后计算各台发动机综合性能到正理想解和负理想解间的欧氏距离，利用综合效能函数发动机性能贴近度来度量各台发动机性能的优劣，对机队中发动机性能进行排序。

通过TOPSIS评估方法可知，该评估方法存在两个不足：逆序和中垂线矛盾问题。在原有机队中加入新的发动机为评估对象时，机队中发动机的正、负理想解就改变，那么计算的性能贴近度也会发生变化，各台发动机原有的性能排序将会被改变。此外，机队中不同台发动机性能评估结果可能距离正理想解的距离近时其距离负理想解的距离也近，即某两台发动机性能可能分别落入正、负理想解之间的同一垂线时，此垂线在正、负理想解中垂线的上方和下方时，那么各台发动机的性能本来是有差异的，但最终的评估结果则有可能是两台发动机性能一致，最终导致评估不准确，甚至错误。

2 TOPSIS评估方法改进

2.1 逆序问题解决方法

如图1左图所示，设M为正理想解，N为负理想解， BN×AM - BM×AN＞0，发动机A的性能比B的动机加入机队后，其正、负理想解M和N变成M'和N'，那么据图1左图有可能得出BN'×AM'- BM'×AN'≤0 ，即发动机A的性能比B发动机的性能好，显然得出的结果与实际是矛盾的。故改变传统TOPSIS法评估模型中提出的以机队中发动机各评估参数值中最差的为负理想解的方法，提出以原点o为绝对负理想解，以100为绝对正理想解，使正负理想解保持绝对不变，则插入新发动机后，原有性能排序不会改变，解决逆序问题。

2.2 中垂线矛盾解决方法

中垂线矛盾问题，如图2左图所示，可以在参数值标准化处理中加以解决：通过将A和B发动机的数据均处理到中垂线CD上方的正方形ENFM内，即数据标准化时将极小值标准化为正理想解的一半，比如正理想解为100，极小值就为50，如图2右图所示。

图2 中垂线矛盾解决方法

故提出对发动机的效益型、成本型和固定型的性能参数在标准化处理时，依据发动机性能参数的属性将各参数标准化后与正理想解的一半相乘并加上正理想解的一半。针对三种属性的性能参数标准化具体公式如下：

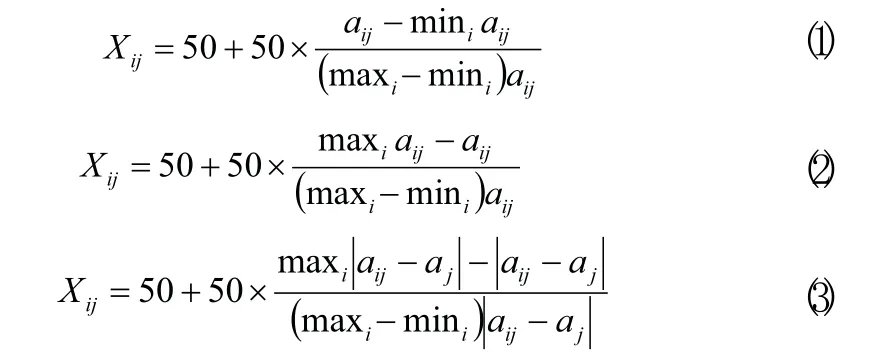
2.3 基于ANP计算发动机性能参数权值

针对发动机性能参数间并不独立的而是相互相关的现实，采用考虑多参数间相关及相关优先度的ANP方法，确定发动机性能参数权值。首先对发动机性能参数对发动机性能的影响类型不同将发动机性能参数分类，并以此构建发动机性能参数层次体系[6]，如图3所示；同时依据各类型发动机性能参数相关性，构建发动机性能参数网络层次体系[7]，如图4所示。

图3 性能参数层次体系

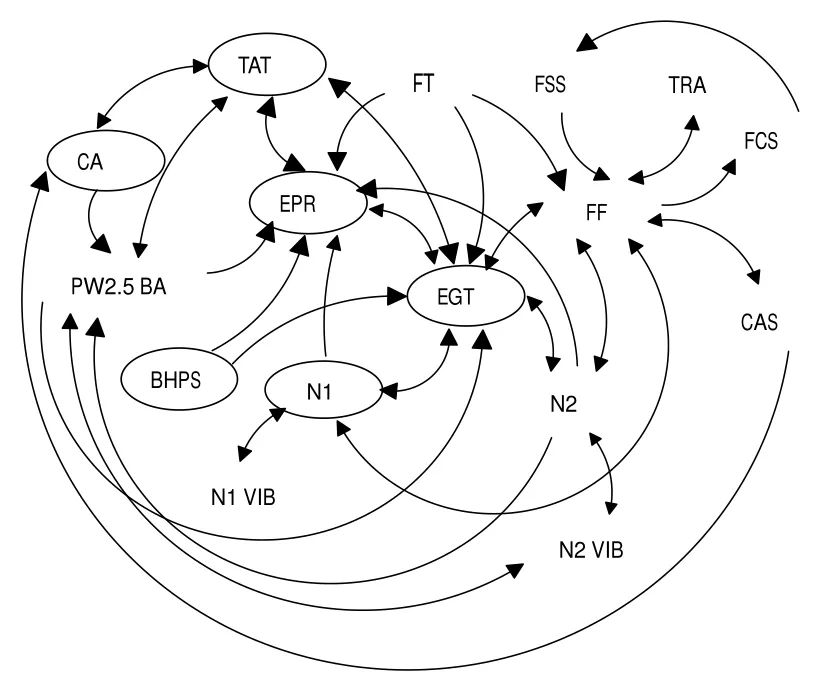
图4 性能参数网络体系

其次构建ANP的超矩阵以计算权重。通过已经构建的发动机性能参数层次体系和网络体系以及确定的各参数之间的相关优先度，建立发动机各性能参数相对其他参数的排序项量，综合得到在某个准则下的超矩阵 Wij。

接着构造航空发动机性能参数加权超矩阵。构造的未加权超矩阵表示的是性能参数某层间各个参数对单个准则的排序，但没有考虑其他层对该准则的关系和影响。故分析各层间影响关系，即将每个单层作为一个性能参数，如气路参数、结构参数等，针对单层进行两两比较判断，并计算相应排序权值，由此得到加权超矩阵。

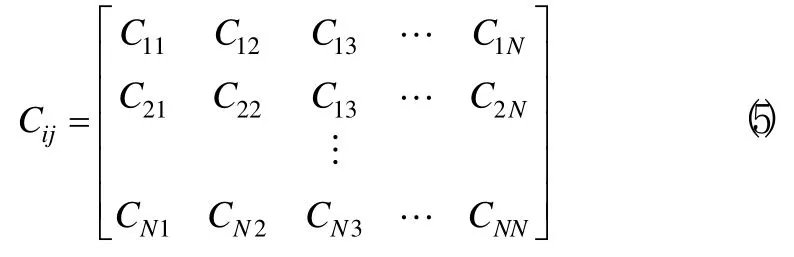
最后求解极限超矩阵。由于性能参数之间存在着相互依存关系或者反馈作用，导致参数之间的影响程度的比较变得复杂。通过对加权超矩阵的极限化处理，得出发动机各性能参数相对于发动机性能这个最高目标的归一化权值。即：

2.4 计算机队中各台发动机性能的贴近度

设机队中发动机 Ai的性能数据向量Ri=(Ri1,Ri2,…,Rin)T，正理想解为 S+=(1 0 0, 1 00,…,100)T、负理想解为 S-=(0 , 0,…,0)T，协方差矩阵为∑的n维总体。由于TOPSIS法中的马氏距离计算中能够用各参数协方差表示各参数数据的相关性，故提出以马氏距离代替欧氏距离来计算机队中各台发动机性能的贴合度。

Ai到正理想解和负理想解的马氏距离分别为：

那么，机队中各台发动机相对贴近度计算方法为：

依据 ci的大小对性能排序： ci越大，性能越好，在翼寿命更长；反之在翼寿命较少。

3 评估模型实例验证

1) 计算发动机性能参数权值

选取某公司PW系列发动机8台进行分析，由于飞机在巡航状态下，运行最为稳定，性能也比较平稳。故提取8台发动机在飞机巡航状态下的数据对8台发动机性能进行排序。

利用ANP法从发动机航后QAR中选取16个主要参数进行分类并构建性能参数层次体系，并分析各参数的相关性，构建性能参数网络体系，通过超级决策软件（super decisions, SD），并在通过一致性检验即判断矩阵一致性CR＜0.1的情况下[8]，获得各性能参数权重，如表1所示。

2) 性能参数标准化处理

对8台发动机巡航阶段性能参数值，根据公式（1,2,3）进行标准化处理，得到矩阵如下：

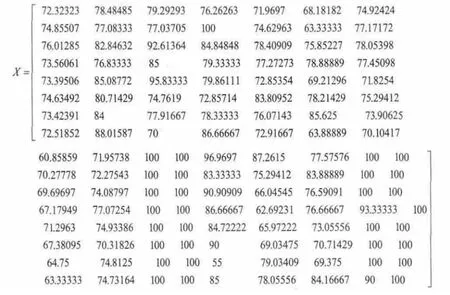
3) 根据式(4)，式(5)求机队中各台发动机性能到正、负理想解的距离：

依据公式（6），计算各台发动机性能贴近度及依此对发动机性能排序。

4 结果比较分析

利用TOPSIS法计算各台发动机性能到正理想解和负理想解的欧氏距离，进而确定发动机机队中各台发动机性能贴合度，并依贴合度进行性能优劣排序的结果如表2所示。

ANP法在定性确定各参数间相关度的基础上，以各参数间的相关优先度构造判断矩阵，定量计算并归一化得到的权重向量，同时验证符合一致性要求，各性能参数权重向量结果如表1所示。结合各台发动机起飞状态下性能参数的归一化值，利用公式（9）计算发动机机队中个台发动机的性能指数，并依性能指数进行性能优劣排序，如表3所示。

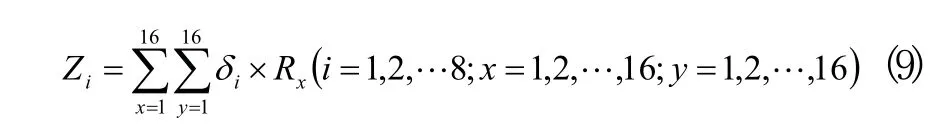
从表3可以分析：改进TOPSIS法和TOPSIS法都是以发动机的性能值距离发动机正、负理想解下的贴合度为发动机机队中各台发动机的性能表示值，贴合度值越大，表示发动机性能值距离正理想解越近，而负理想解越远，即发动机性能在机队中最好；而ANP法则以性能分数表示机队中各台发动机性能表示值，性能分数越大，说明发动机性能在机队中最好。依改进TOPSIS法和TOPSIS法评估的发动机性能结果分析：机队中A1，A2，A7和A8发动机的性能排序只差1；而A3，A4，A5和A6发动机的性能排序差异分别为3，3，4，2，故可以得出，通过对TOPSIS性能评估方法改进，机队中发动机性能排序变化较大。而从改进TOPSIS法和ANP法评估的发动机性能结果来看：机队中A1发动机的性能排序只差2，而A3，A4，A6和A7发动机的性能排序差异分别为1，1，1，1；A2，A5和A8发动机的性能排序则保持一致，故可以得出，通过对TOPSIS性能评估方法改进，机队中发动机性能排序变化基本很小，其中3台发动机的性能排序两种方法的评估结果保持一致。

故通过对3种评估方法得出的发动机机队性能排序结果，可以得出：通过以原点而不是以各发动机性能参数差值为负理想解、利用样本协方差矩阵反映参数间相关性和以ANP法确定各参数权值并以马氏距离而不是欧氏距离来计算发动机性能的贴合度等改进TOPSIS法，重构的发动机性能评估模型解决了TOPSIS法模型不足引起的评估结果偏差较大的问题，同时通过ANP法评估得出的结果说明改进TOPSIS法得到的发动机性能排序具有可行性。

5 结论

1) 通过对TOPSIS评估方法的分析，提出以原点o为绝对负理想解，以100为绝对正理想解，使正负理想解始终保持绝对不变，解决逆序问题；提出依据发动机性能各参数属性的不同而采用不同的方法，但是都要将各参数标准化后与正理想解的一半相乘并加上正理想解的一半，解决中垂线矛盾问题。

2) 针对TOPSIS评估方法中，发动机多性能参数权值难以合理确定的问题，提出ANP法将发动机性能参数依不同属性分层，同时考虑参数间相关优先度，准确获取权值。

3) 针对发动机性能参数间存在的相关性，提出以马氏距离而不是欧氏距离来计算发动机性能的贴合度，其中包含了各参数间的协方差，降低发动机性能信息重叠，提高计算速度。

表2 改进TOPSIS法、TOPSIS法及ANP法发动机性能评估结果

[1] 张海军,左洪福,梁剑.航空发动机多指标模糊信息熵的性能排序研究[J]. 应用科学学报,2006,24(3):288-292.

[2] 杨皓翔,梁川,侯小波.改进的TOPSIS模型在地下水水质评价中的应用[J].南水北调与水利科技,2012, (5):51-55.

[3] 肖淳,邵东国,杨丰顺.基于改进TOPSIS法的流域初始水权分配模型[J].武汉大学学报（工学版）,2012,45(3):329-334.

[4] Karimi M, Moztarzadeh F,Pakzad A. Application of Fuzzy TOPSIS for Group Decision making in Evaluating Financial Risk Management, 2012[C].Malacca, Malaysia,2012 International Conference on Innovation, Management and Technology Research (ICIMTR2012),2012:215-218.

[5] 栾圣罡.基于气路参数样本的航空发动机状态监控监视方法与系统研究[D]. 哈尔滨:哈尔滨工业大学,2008.

[6] Karimi M, Moztarzadeh F, Pakzad A. Application of Fuzzy TOPSIS for Group Decision making in Evaluating Financial Risk Management,2012[C].Malacca, Malaysia,2012 International Conference on Innovation, Management and Technology Research (ICIMTR2012),2012:215-218.

[7] 陈可嘉,于先康.逆向物流服务供应商选择的ANP方法及Super Decisions软件实现[J].福州大学学报（自然科学版）,2012,40(1):31-37.