射频仿真系统中天线阵列在空间位置和布局设计＊

赵 泉 孔令峰

（中国船舶重工集团公司第723研究所 扬州 225001）

1 引言

随首雷达对抗辐射式仿真的发展、导弹导引头测试要求的不断提高，国内建起了大量功能各异的微波暗室，其中以辐射式仿真暗室为最［1］，世界各国高度重视，并得到极大发展，尤其是美国的仿真技术应用最为全面［2］。整个系统最关键的环节是三元组天线阵列的精度控制，它直接影响到仿真试验的精度。早在上世纪70年代，美国波音公司提出了沿用至今的角闪烁方程（幅度重心公式），为射频仿真系统的发展奠定了基础［3］。球阵面天线阵列的设计是保证目标位置精度的基本条件，天线三元组在球阵面上位置坐标直接影响到后续阵列结构的设计。

2 天线阵布局的几种方案

球阵面天线阵列除了设计成三元组外，也可设计成四元组，但是不难证明，在技术指标相同的条件下，三元组面阵所需的微波器件数量要比四元组面阵省得多。天线阵的形状一般有圆形、六边形、矩形及官帽形等，图1中圆形面阵和六边形面阵单元布置图的例子在最大尺寸相同的情况下，圆形面阵的视场角要比六边形的略大些。

但从图1中可知，六边形的优点是天线辐射单元的利用率高，成本最省。国外仿真试验室的天线阵主要采用这两种形状，尤其是用于雷达导引头的仿真试验，采用圆形面阵比较多，其视场角一般都能满足要求，而且在各个方向上的视场角基本相同。但对于开展导弹末制导回路的仿真试验，尤其是考虑到在弹道末段的快速变轨情况，要求很大的视场角才能满足试验要求。这时，面阵应当设计成矩形，而且微波暗室的横向尺寸相应地要加大。有时甚至设计成矩形面阵的视场角还满足不了要求，这时只能将弹道分段做试验。至于官帽形面阵一般是为了节省经费只能满足特定方向上的大视场角要求，在其余方向上的视场角都比较小［4］。

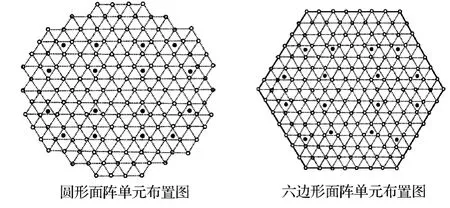
图1 三元组天线阵列布局图

3 球面三角形内角的理论计算分析

由于射频仿真要求利用三个天线不同幅度的变化来模拟三角形内部的目标点的运动，根据幅度重心公式的原理可知，三个天线距离转台中心的距离必须是相等。而射频仿真中的天线数量一般都较多，其天线布局一般如图1所示，但实际在空间布局上，每个天线都应该在一个等半径的球面上，因此相邻三个辐射天线所组成的是球面三角形。

而在以往较多的文章中提及三元组中球面三角形为球面等边三角形［5～7］，而笔者通过计算发现如图1所示在球面上所有辐射天线组成的三元组并不是所有的三角形都是球面等边三角形的。

假定球面阵中天线单元间距为D＝48mrad［8］。如图2所示，有六个球面三角形，分别为△agb，△afg，△bgc，△cgd，△dgf，△cgf。

以△agb为例，三条边对应的张角分别为48mrad。如图2所示的六个三角形如果是平面三角形，则完全可形成封闭的六个等边三角形，而对于球面三角形，则要根据球面三角形计算，利用球面三角形计算公式［9］：

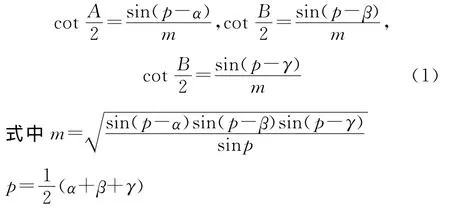
式中：α，β，γ分别为球面三角形边的张角；A，B，C分别为三条边对应的球面三角形的角。

通过式（1）计算可知，图2中△agb三个角度为60.0191°。图中6个球面三角形假设都是等边三角形，则每个面三角形的角度都是60.0191°，则∠agb＋∠bgc＋∠cgd＋∠dge＋∠dge＋∠egf＝60.0191＊6＝360.115°＞360°，则通过计算六个角度的和可以明显看出，圆周角大于360°，因此假设不成立，证明图2所示的六个球面三角形不可能是等边三角形。

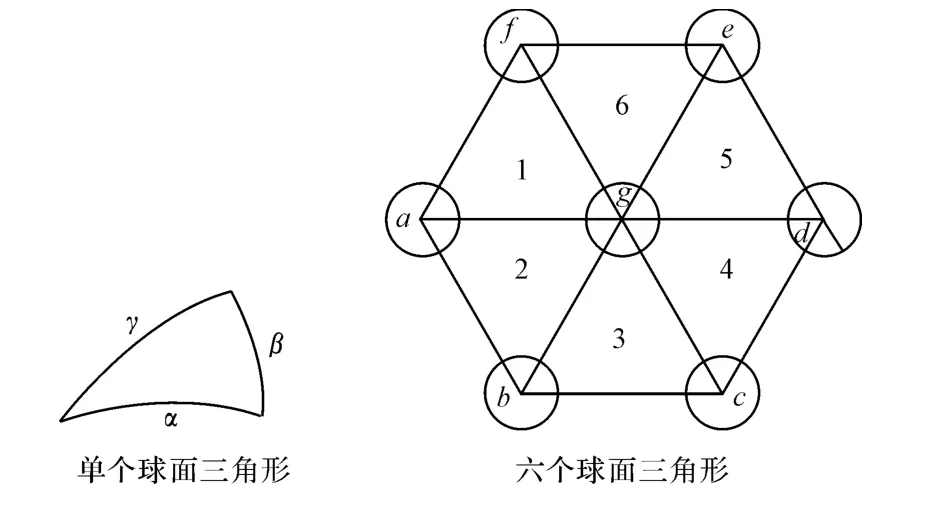
图2 球面三角形示意图

以上是以三元组阵元的张角为48mrad计算得出的结果，而对于张角的选择并不是任意值，它取决于被试雷达天线的波束宽度及模拟的精度，不同的张角在辐射式仿真试验中对试验精度有不同的影响。

是否存在一个确定的张角满足在球面上形成如图2所示的由六个球面等边三角形形成的球面六边形呢？答案是否定的。现假设存在，则每个球面等边三角形的角度都为60°。通过式（2）计算球面等边三角形的张角。

通过公式（2）计算可知，p＝90°，代入m的计算公式发现m无解，即无法求得球面等边三角形的张角，则可得出结论：无论球面等边三角形的张角为何值，都不存在如图2所示的，能够形成六个球面等边三角形组成的六边形。

4 目标球面位置的理论计算

三元组在球面阵上的坐标计算公式如下［10］：

假设坐标原点在球心，采用右手坐标系统如图3所示。

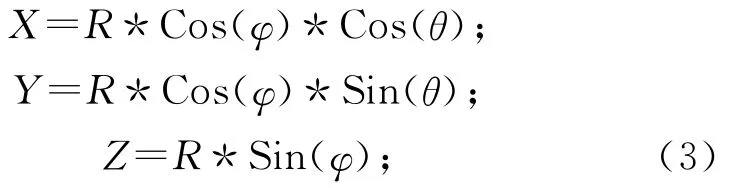
关于球面三角形的形状，也可能通过几何关系进行分析。在球阵面上，天线单元分为若干层，每

一层相邻单元天线间隔相对于各层水平截面的圆心角是三元组的张角，每层单元相对于球中心（即转台中心）为仰角的整数倍，即在俯仰方向上相邻层的天线单元相对于转台中心的夹角相等，天线单元按三元组的形式排列。设中心水平截面为0层，上下对称排列，则相邻层之间的三角形全部为等腰三角形，底边在同一层上的三角形尺寸都相同，三角形底边因地球仪原理向上（或下）有所缩小，并且向上（或下）减小的速度逐渐加快，因此在球面阵中三元组越往上（往下），球面三角形中的底相对于腰越短的趋势。

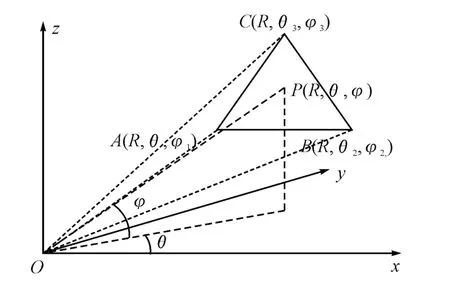
图3 三元组坐标示意图

假设面阵半径R＝20000mm，三元组张角48mrad，从中心层向上共六层为例，计算结果所表一所示，每层三元组的弧长见表1.

表1 各层三元组底边与腰的误差列表

从表1可以明显看出，在面阵中的各层三元组会随着层数的增加，三元组底边与腰的长度差越来越大，不再是误差很小的球面等边三角形。

5 结语

本文从射频仿真阵列结构中辐射天线布局出发，分析研究了几种天线的布局方式，分析论证了相关文章中提及利用球面等边三角形的幅度重心公式，来模拟产生目标运动的问题。阐明了本文的论点，同时对本文论点进行了证明。通过本文的阐述，帮助未来天线阵列设计者，充分考虑到三元组在球面的布局，提高以后在目标位置模拟精度、定位误差分析、三元组近场修正的工作效率，优化了射频仿真阵列设计。

［1］方辉熠，李启权，陈洲达.防空导弹武器系统仿真［M］.北京：宇航出版社，1995.

［2］Mike F，Wacker.Use Allan Vaniance To Characterize Oscillator Stability［J］.Microwave＆RF，1997：92－190.

［3］A A Polkinghorne，et al.Radio Frequency Simulation System（RFSS）System Design Handbook［R］.Boeing Company D243－10004－1，1975.

［4］倪虹，路军杰，等.射频仿真系统天线阵设计方案评述［J］.战术导弹技术，2010（4）：104－109.

［5］江伟明.辐射式仿真试验三元组天线阵元张角对被试设备性能仿真影响研究［J］.舰船电子工程，2007，27（3）：88－91.

［6］王泗宏，黄惠明，等.射频仿真幅相控制误差对目标位置精度的影响分析［J］.飞行器控制学报，2007，26（2）：59－63.

［7］蒋庆平，刘晓宁，等.弹箭与制导学报，2006，26（1）：282－285.

［8］毛继志，郭陈江，等.幅相误差对射频仿真系统目标位置精度的影响［J］.系统仿真学报，2003（8）：1149－1151.

［9］叶其孝，沈永欢.实用数学手册［M］.第2版.北京：科学出版社，2006：51－55.

［10］潘忠堂，周德兴.射频仿真系统阵列结构设计综述［J］.雷达与对抗，1999（4）：43－48.