“我要做数学大人”——3C①知识形成漫谈
●郑大明
一天, 孙子用积木摆了一座如图1 所示的 “房子”。

图1
我问他:“积木是什么样子的呀?它们有几个?”他说:“方形的,三个;三角形的一个呀! ”接着他告诉我,老师只问了他们每个积木的颜色和软硬。 我告诉他,爷爷这个叫数学问法,老师那个叫物理问法。 等以后长大了, 两种你都会问了。 他高兴地说:“我要做数学大人,还要做物理大人。 ”
是呀,孙子要做“数学大人”。 我就琢磨,他怎样才能从“数学幼儿”变成“数学大人”呢? 需要有什么本领才是“数学大人”呢?
《数学课程标准》(2011 版) 开篇就指出:“数学是研究数量关系和空间形式的科学”。数量关系是什么呢? 通俗地讲就是关于事物的个数以及事物的多与少,大与小,长与短等信息。空间形式又是什么?就是关于事物的样子即形状, 以及事物所在的位置比如上边或者下边、前面或者后面,还有事物运动的方式比如汽车轮子是滚动着走的还是滑动着走等信息。如果把握了数学的这个本质内涵,我们就知道如何把小孩子培养成“数学大人”了。
一、学会数学地认知:有数学家的耳朵和眼睛
我们认识一样东西,心理学上叫做认知。数学认知就是用数学家感知和认识事物的方法去收集事物的信息。 如果你会用数学家的看、听、摸等方法去收集信息了,你就形成“数学认知”本领了。
《数学课程标准》(2011 版)提出了数学家认知事物的三个本领,即数感、空间观念和数据分析观念。
所谓数感,就是想到用看、听和摸等方式了解事物的个数或多少的本领。 如图2,一盘鸡蛋多少个?一筐鸡蛋多少个?
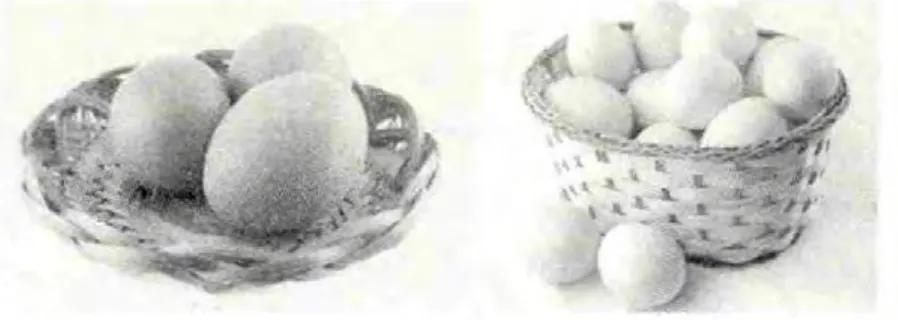
图2
一盘鸡蛋个数少,正常人用眼睛一看,边看边数边念,一,二,三。 你就知道了鸡蛋是3 个,旁边的人也听到了鸡蛋是3 个。 瞎子怎么办? 听你边念边数,也知道了。他也可以自己用手边摸边数,知道鸡蛋是3 个。一筐鸡蛋,你能只看就数出来了吗?那不行,有些被遮住了,需要分拣出来,边捡边数了。
同时,通过这些信息收集活动,你也就知道了盘子里面的鸡蛋个数比筐子里的少,反过来筐子里的鸡蛋比盘子里的多。
所谓空间观念,就是想到用形状、方位、位置、运动等知识去了解事物的本领。
如图3,看到这个箱子图片你想说些什么?

图3

图4
“箱子是木头做的。”这不是数学家的眼光。数学家说:“箱子是正方体形状的。 ”“箱子有一个面用木条钉成三角形了。”“箱子的6 个面都钉了木块。”“钉有斜木条的面不在前面,也不再上面。”“箱子不容易滚动;容易推着滑动,也就是平移。 ”
当然,空间观念还包括“看图形想实物”,“看句子想图形、想位置或者画图形”等内容。 如图4,根据下面的图形设计制作一个礼品盒, 并在上面贴一朵花,在周围画上卡通画或者写上祝福语。
所谓数据分析观念, 就是能想到用收集数据的方法研究一些事物或者现象发生的情况以及预测其发展势头的本领。
如,家长:“请问张老师,五年级的3 个班,哪个班好一些,我想把孩子转到那个班去。 ”张老师:“3个都还可以,转哪个班都没问题。 ”
数学家:“请问同学们,五年级的3 个班,哪个班好一些? 我们想知道哪些班能保持‘优秀班集体’。 ”
学生:“你去查看各班的成绩单吧,老师那有。 ”“你去班上问同学嘛! ”
数学家看成绩单和到班上去问学生, 都是调查研究、采集数据和分析情况的好方法。拿到成绩单数一数,排一排,就知道哪个班成绩好,成绩好的人数有多少。问同学就知道哪个班表现好了。有了这个本领就不会像张老师那样回答:“都可以。 ”或者“二班好点。 ”这样回答,没有说服人的证据或者理由。
数学家认知事物,最重要的就是有序地认知。认知时做到依次序,不重复不漏掉需要认知的东西。
数鸡蛋等事物的个数, 一般按照由少到多的顺序,一个一个地、一十一十地接着往下数;数水果等几种事物的个数,就要先分开苹果啊、香蕉啊和梨啊,分类以后再从少到多地数;数家里来的客人,就要从屋里到屋外依次一个一个地数完;看箱子有几个面,就要从上到下,从左往右,从前往后依次数完6 个面。
像给你一个圆形,叫你联想真实的事物,你就得从身边近的东西开始观察,再到离自己远的东西。先看身边的钟表、杯子、碗等,再看远处的汽车轮子、风车,再想天上的太阳、月亮;从熟悉的东西开始慢慢到陌生的东西。
二、学会数学地表达:有数学家的嘴巴和铅笔
我们说话,在心理学上叫做表达。表达的目的是传播或者交流信息, 是一个人向另一个人或一群人传播或者交流信息。有了这种本领,你就能够在人群中相互沟通了。表达经过无记录到有记录地发展,分为口头表达和书面表达。口头表达就是用嘴说,用声音符号传达信息; 书面表达在白纸或者电脑等东西上用文字和图形符号传递信息。
《数学课程标准》(2011 版)提出了数学家表达信息的两个本领,即符号意识和几何直观。
所谓符号意识,就是想到了用约定的、统一的数学符号来传播所了解到的事物信息的本领。
数学家常用的符号有文字符号如一、二、三等,数字符号如 0,1,2,3 等, 字母符号如 a、b、c 和 x、y、z等,几何符号如点、线、面、体等,图形符号如〇、☉、☆、□等。 还有许多规定的符号如“>、<、=、( )、[ ]”等。
数学家用的声音符号,就是指对每一种文字、数字和几何符号等,都规定一个对应的读音(每个不同的民族或者国家, 对同一个符号的读音都不一定相同)。或者反过来说,对生活中人们的读音,都对应一个文字、数字或者几何符号等去记录。 比如“0”读作“零”,“=”读作等于;“☉”读作圆。
有了这些符号我们就能传播和记录事物的大小、多少、形状等数学信息了,就能像数学家那样说话了。 例“三角形什么样子的? ”“三角形有 3 个角,3条边,3 个顶点”。
所谓几何直观, 就是想到了用约定的几何符号点、线、面、体等来传播一些没有形状特点的事物或现象的本领。比如记录天气变化的天气实况图,记录心脏律动的心电图等,都不是真正意义上的有形事物,但是我们用上几何元素表示,就能直观地说明问题。如图5,这些交通标志牌上的几何图形符号,简单明白地给司机们提示了哪些能行走、哪些不能行走、要注意些什么的信息。你想,要是每个需要提示的地方派一个人或者一个大喇叭在那里 “哇啦哇啦” 地提示,那效果会是怎样的呢?

图5
这里的图形符号表示的是一种交通运行现象或者行为状态,而不是一个事物真实的形状或者样子。
如图6 是一张汕头市平均月气温和降水量统计图。这里的温度和降水量也是一个没有形状的事物,但是通过用这些点、线和直条表达出来,人们一下就能感受它们的存在,也能很容易地知道了它们的发展变化状态,可以预测明年大致每个月的气温和降水量的情况了。
数学家说话,最重要的就是注意了以下四点:
一是客观真实。 数学不允许像童话故事那样瞎编。 比如,小明说:“超人奥特曼昨天给我200 元钱,今天早上买了2 个包子和1 碗稀饭,还剩193 元。 ”
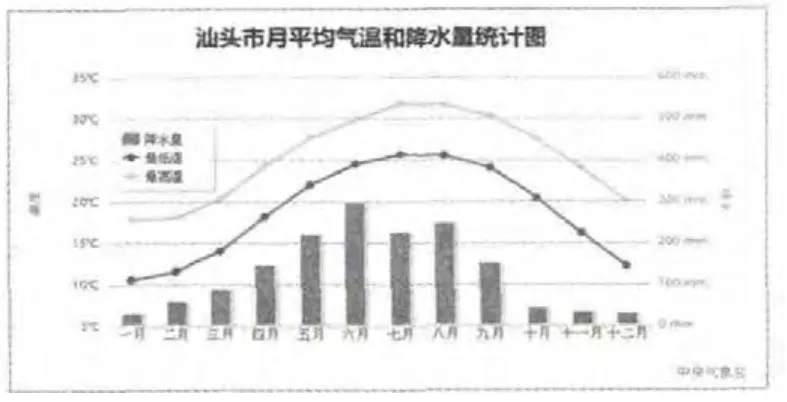
图6
二是科学准确。使用数学语言,不管是声音符号还是文字、字母符号,都不能用错了,因为用错了别人就听不懂或者看不懂了。 比如135,读音记录为一百三十五,不能写成“一白山石午”。也不能用模棱两可的语言或者符号。 比如“一头牛重四百1000 克。 ”这里的“1000 克”和“1 千克”,看起来意义上好像区别不大,但是在计数规则上,就不一样。 1000 克是以“1 克”为计量的标准单位,意思是 1000 个“1 克”;而1 千克是以“千克”为计量的标准单位,意思是1 个“1 千克”。 因此,应该写成“一头牛重 400 千克。 ”
三是简单明了。数学家表达的特点是简单。比如交通标志的第一和第二排,一看图形就明白意思,就不需要加文字。 第三排比较复杂, 就加了简单的文字。通常来讲,如果一个词语或者一个符号能说清楚的,就绝不使用两个。
四是图文并茂。表达比较复杂的事物,往往需要文字符号与图片、图形或者图形符号一起使用,才方便说清楚意思。 比如上面图5 的“禁行标识”和图6的“气温和降水量统计图”,既有文字说明,又有符号、图形等。
三、学会数学地思考:有数学家的大脑和胸襟
我们想问题,在心理学上叫做思考,想的过程叫做思维。数学家想问题,有两个关键,一个是情绪,一个是方式。也就是说,一要静下心来,心平气和,不偏不倚,实事求是,在社会学里面叫做中立,在数学上叫做理性精神。二要有思考的路径,从哪里开始到哪里结束,用什么作参照,用什么做比较,他们都有相应办法。 如果没有这些东西作支撑,就可能胡思乱想,没有结果。
《数学课程标准》(2011 版)提出了数学家想问题的两个本领,即模型思想和推理能力。
所谓模型思想,就是想到了要建立若干个想问题的参照标准的本领。 这些参照标准既可以是生活中有的东西,也可以是我们大家约定俗成的一些东西。 像雷锋叔叔,就是生活中的好人模型。 一说做好事了,大家马上就想到和雷锋叔叔比一比,看自己做的是不是雷锋做的那些好事。
数学家塑造了许许多多这样的标准化模型。 比如,数的模型与加法模型。 如表1 中的实物,我们发现苹果、 蜜蜂和足球, 在生活中他们几乎没什么联系。但是在表格中,数每一列事物个数的次数也就是频率是一样的。 因此, 我们先用点子表示数数的次数,有了数数的模型。 再给他一个读音,有了“yī、èr、sān、sì”这样的声音模型,我们就可以说话了。以后数任何东西,凡是数“●”的,就说“yī”,数“●●”的,就说“èr”。 嘴上能说了,数学家又规定了写数的符号化模型“一、二、三、四......”,再后来引进了国际上通用的阿拉伯数字符号“1,2,3,4……”进行书写。

表1
如表2 中的点字图,呈现了加法模型的基本形成过程,从若干个类似的黑白点子组合,抽象出两部分合成一个整体的过程,再用语言和式子记录这个过程。于是,整个一个从点子模型到式子模型的加法模型就形成了。

表2
后来,数学家还发现这个模型中的两部分,无论先写哪一部分,结果都是一样的。 于是出现了A+B=B+A 以及7=1+6=2+5=3+4 的衍生模型。
类似的模型还很多种类,如图7 中(1)是计数单位的模型;(2)计量单位的模型;(3)基本图形的模型。有了这些基本的模型,我们就可以借助它们思考和研究更复杂的问题。
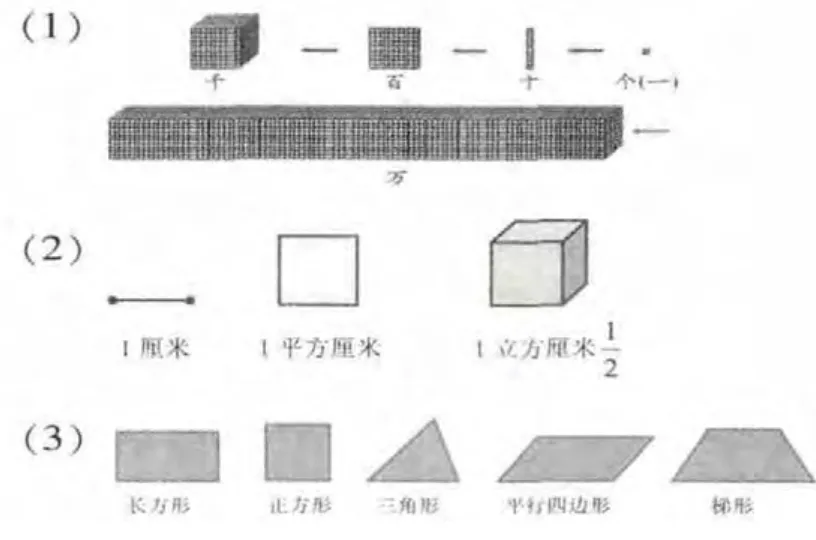
图7
所谓推理能力,就是想到运用已知模型或者研究出的结论进行肯定与否定,从而得出新结论的本领。 这里涉及两个词语,概念和判断。 利用概念对事物的某些特征进行肯定和否定,就是判断。
西方人把推理过程叫做逻辑 (源自古典希腊语logos)。逻辑三要素是概念、判断和推理。上面讲了推理和判断,现在说说概念。
概念就是数学家想问题时使用的参照标准,也就是基本模型。从前面的研究发现,有些模型是生活中的实物或者数学家根据事物共同的形状特点约定的图形元素,用起来很直观、很形象;有些模型没有实物或者事物的图形元素做标准,只能靠语言、文字来进行说明的,比如“加法”“负数”“圆周率”等。 于是,逻辑学上把借助实物或图形元素想问题的过程,叫做形象思维; 借助非实物或者图形元素想问题的过程,叫做抽象思维。
逻辑学上还把推理分为归纳推理和演绎推理等几种形式。 所谓归纳推理就是举出许多实物或者基本模型的共同点进行综合判断,得出新结论的过程。
如图8,看图片,孩子们很容易发现这些昆虫的共同点得出结论:“昆虫都有6 只脚和1 对翅膀”。

图8
一些同学还能马上举出蜜蜂、蝉、蝴蝶、金龟子、天牛子等等都是昆虫的例子。也有同学会产生疑问:昆虫不是都有1 对翅膀吗?跳蚤的翅膀呢?最后查阅资料,才发现跳蚤的翅膀退化了,属于变态昆虫。 但跳蚤的腿脚很发达,于是才跳着走的。
这就属于演绎推理了。所谓演绎推理,就是运用已知结论对需要作出判断的事物或现象进行对比判断得出新结论的过程。 因为,昆虫都有一对翅膀,是先前的结论。既然跳蚤是昆虫,那么跳蚤的翅膀在哪里?
按照形式逻辑的演绎推理三段论格式表达上述过程就是:

四、学会数学地运用:有数学家的双手和双脚
我们做事情,要用到我们的身体和学来的知识,这在心理学上就叫做运用。 前面讲的都是数学家怎样运用自己的眼睛、嘴巴、耳朵和大脑了解事物的信息和想问题。 其实,要像数学家那样做事情,前面讲的那些就是关键的组成要素。 如果你不会看, 不会说,不会想,就谈不上会做。 即使你照着别人设计好的图纸、想好的方案、摆好的模型模仿一辈子,你也很难有自己的思想和方法,做不出大的成绩来。因此我们说“学会数学地做”就是要像数学家那样,自己看,自己想,自己说,自己做。这就是《数学课程标准》(2011 版)上告诉的数学家做事情两个关键本领,即创新意识和实践能力。
所谓实践能力就是包括照着别人的图纸与方案模仿做事情和自己独立做事情的本领。
所谓创新意识就是专指自己独立看、 自己独立说、自己独立想、自己独立做的本领了,而且特别强调你要看到别人没有看到的,说出别人没有说出的,想到别人没有想到的,做出别人没有做出的。
同时,《数学课程标准》(2011 版)还告诉了数学家做事情的一个专项本领,即运算能力。
很多人认为,现在有计算机了,这个本领没啥用了。 其实,数学家具备的运算能力,不是把自己训练成会计算题目的机器,而是具备一种态度和一种规则意识。即做任何事情都要一丝不苟和按规则办事。就像计算数学题,不专心观察、不认真书写、注意力不集中就容易出错; 不按运算法则去做就很难找到合适的答案。 比如“先乘除,后加减;先括号里,再括号外”是先辈或者大家共同总结出来的规则,你照着做就会很快得出答案。 但是,如果遇到特殊数据,你会尝试按照一些规律和性质改变一下运算顺序,就会找到简便的算法,更快更好地完成任务。如果再遇到更特殊的运算数据,完全靠自己去寻找更新、更独特的思路和算法, 得出答案或结论, 你就是数学家了。 比如,成功发布“陈式定理”的陈景润、成功创造“统筹优选法”的华罗庚、成功解决“孪生素数界限问题”的张益唐等,就是这样的数学家。
因此,我们学习数学家做事,那么长大后如果按照一定的规则办事,就会很顺利地完成任务。如果我们解决问题过程中还学会了自己看、 自己想、 自己说、自己做,练就了“发现问题、提出问题、分析问题和解决问题”的本领,那你就是真正的“数学大人”。

