融合FFT与小波的电力谐波检测技术的探讨

童 晋

（合肥工业大学 电气工程学院，安徽 合肥 230009）

融合FFT与小波的电力谐波检测技术的探讨

童 晋

（合肥工业大学 电气工程学院，安徽 合肥 230009）

比较FFT和小波变换理论，结合两者共同点及不足，尝试以FFT为主、小波去噪相辅的方法提高谐波检测的准确度。借助MATLAB中小波工具箱中的多种阀值函数，对模拟信号进行降噪、去噪处理，尽可能使其接近原始信号的波形，并利用 FFT对去噪以后的信号进行分析，提取幅值图进行比较，以检测该方法在谐波检测系统或装置中的应用的可行性。仿真实验结果表明，一定条件下，融合FFT与小波变换理论在应用于谐波检测上有更高的准确度和有效性及存在应用于实践中的可能性。

电力系统；谐波检测；FFT；小波分析；MATLAB仿真

近年来，伴随着大量可靠、快速、廉价的电力电子阀在电力行业各个部门的广泛应用，谐波问题也伴随其成为电力系统工作者们一个新的研究挑战。谐波是一种干扰量，它会影响到电网的整体电气环境，对各类设备的正常运行产生干扰。

1 谐波问题研究的起源

早在二十世纪五六十年代，E.WKimbark便在其著作中对有关变流器引起的电力系统谐波问题进行了总结。1992年，CENELEC正式颁布了《公用配电系统供电特性》，并将其作为当时的欧洲共同体对电能质量的统一标准，其中，为中低压配电系统用户供电端的电能质量作了制定全面的规定[1]。

我国对电力系统谐波问题的研究起步较晚。1982年，我国首次谐波学术研讨会第一次针对石太电气化铁路中出现的谐波问题，以及由此引起的电力电容器损坏等问题进行了讨论，这是我国开展有关谐波研究工作的开端。而现今，在我国实行的国家标准《电能质量一公用电网谐波》中，针对谐波的主要指标包括：n次谐波电压含有率、谐波电压、电压谐波总畸变率[2-3]。

在各类谐波问题中，谐波检测是其一重要分支，对于抑制谐波有着极其重要的指导作用，因此，对谐波的分析与测量是分析控制电力系统工作中一项极为重要的工作。在检测工作迅猛发展的这数十年间，先后诞生了频域理论和时域理论，并据此形成了多种谐波检测方法：模拟滤波、傅立叶变换、小波变换、瞬时无功功率理论、神经网络等。本次研究尝试着将FFT与小波变换结合起来，探讨其使用的可能性。

2 FFT和小波理论综述

2.1 快速傅立叶变换（FFT）算法

FFT是由J.W.Cooley和J.W.Tukey于1965年提出，在对有限长序列通过DFT将其频域离散化成有限长序列时，因其计算量大，无法实时处理问题，于是引出了FFT。它利用指数函数的周期性、对称性以及正交性，将离散傅立叶变换（DFT）的计算量大幅度减少。

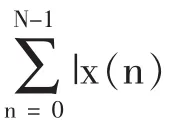
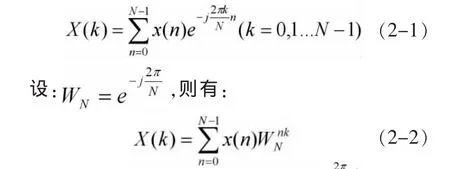
利用这些特性，可以将DFT运算中的部分项合并，并使DFT运算分解为若干个小点数的DFT。因为DFT的计算量与成正比，所以N越小，计算量也就越小[4]。

2.2 小波分析法理论

小波分析是著名科学家 Y.Meyer于20世纪80年代构造出来的，后在与S.Mallat合作下，共同建立了构造小波基的方法和如何进行多尺度分析。小波变换是一种时域面积固定而形状可发生多项改变的时频局部化分析方法。因此，它可以从复杂信号中提取有效信息，并通过其自身可伸缩、平移等特性对信号进行多尺度地细化分析，从而可以解决许多傅里叶变换无法分析的问题。该方法在低频部分具有较低的时间分辨率和较高的频率分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，而因于此，使得小波变换具有对信号的自适应性[5]。

将小波变换运用到谐波分析中，就是利用小波的运算特性来滤除频率较高的频带上的信号分量：将含有谐波的信号分解开，得到多个不同频率的信号，把低频带上的分量作为基频分量，则将高频带上的分量可视为各次谐波分量，据此便可以求得所需谐波信息。在小波分解完成后，不同的尺度可以具有不同的时域和频域分辨率，借此可以将不同频率范围包含的信号分离出来，从而达到谐波检测的目的。将小波变换用于谐波检测时，小波基函数和分解层数的选取非常重要，如果小波基函数和分解层数选取合适，则可以得到很好的检测结果。在本研究中，因时间及研究水平有限，兹采用MATLAB小波工具箱中自带的小波函数进行实验。

使用小波进行去噪的过程主要分为以下三个步骤：

⑴ 选择小波基函数，确定小波分解层数，对输入信号作小波分解（本文采用sym8小波，分别进行5层和2层分解进行对比讨论）[6]：

其中，y表示输入信号向量y1，y2， …yn，f是真实信号向量f1，f2，…fn，z是高斯随机向量z1，z2，…zn。

⑵对小波系数W0作门限阈值处理 （本次研究采用MATLAB自带的四种阀值，在不同小波分解系数下进行分析），如：

门限阈值处理是去噪过程中极为重要的一步，如果阀值过小，则无法完全去除噪声分量，而如果阀值过大，会损害信号中的有效信息，造成输出信号失真，影响测量结果。

⑶ 重构信号[7]：

根据阀值化处理后的高频和未处理的低频小波系数进行信号重构，得到去噪后信号。

2.3 FFT与小波理论在谐波检测中的比较及评述

针对FFT与小波之间相辅相成的关系，及这两者之间存在的差异性：在小波变换中，可以准确地确定发生突变的时刻，以滤除干扰信号，但无法准确快捷地分辨出各次谐波；而傅立叶变换则可以较为准确地测出平稳波形中的各次谐波幅值。从确定突发信号起止时间以及提高系统信号监测的准确性的角度上来看，小波变换优于傅立叶变换，但又因为在测量中需要测出电压等级下各次谐波成分的含有率，所以必然需要傅立叶变换的存在。

对于各电压等级下各次谐波成分的含有率而言，傅立叶变换最大的缺陷在于其不能够聚焦到信号的每个细节，继而进行多分辨率的时频分析，它没办法很好地消除畸变信号以及突发信号造成的误差，而小波分析恰恰擅长于此。因而我们可以大胆的进行尝试：利用小波变换的原理对信号进行去噪处理后，保留信号本身所含有的周期性信号，然后对已去噪信号进行FFT分析，便可以得到相较于一般FFT法测量值更为准确的测量数据。

本文通过进一步研究，探讨将傅立叶变换和小波变换融合在一起，利用两者的优点，将之应用于电力系统谐波信号的分析。

3 MATLAB仿真研究

3.1 仿真中使用的MATLAB阀值

在MATLAB中有4种阈值函数形式可以选用[8-9]:

rigrsure:基于无偏似然估计原理进行阈值选择，先确定一个给定阈值的风险估计，再选择其中风险最小的阈值t*作为最终选择。

sqtwolog:长度对数采用固定的阈值形式,这种阈值形式在软门限阈值处理中能够得到直观意义上很好的去噪效果。

heursure：启发式阈值它是rigrsure和sqtwolog两者的综合：当输入信号信噪比很小时,估计有很大的噪声，这时heursure采用固定阈值sqtwolog。

minimaxi：最小极大原理选择的阈值，同sqtwolog类似，这是一种固定阈值，通过产生一个最小均方误差的极值，在信号中实现最大均方误差最小化，计算公式为:

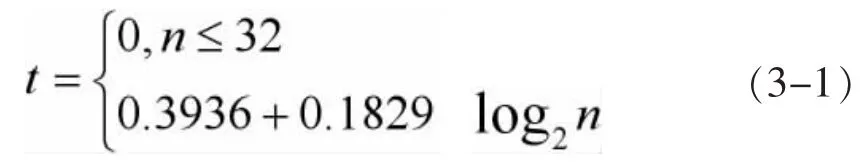
3.2 仿真分析

因为本文主旨讨论在降低电力系统谐波时应用小波去噪的可行性，为方便计算及验证结果，故仅采用整次谐波进行分析讨论。

而在实际应用中的噪声信号种类很多，但因为实验条件等原因，本次研究仅使用MATLAB中的randn作为噪声影响。

通过使用MATLAB中固有的四种阀值函数对其进行一维小波去噪后进行傅立叶变换求得幅值，通过对比原函数处理结果来分析探讨融合小波去噪与FFT算法是否能提高在电力系统谐波测量过程中的精度。通过多种阀值函数处理来了解不同的阀值函数会对波形、幅值产生什么样的影响，以讨论去芜存菁的可能性。并通过利用不同小波分解层数实验，观察小波分解对原函数影响来了解能否存在在许可条件下降低其对原函数的影响的可能性。

大体流程图如下：

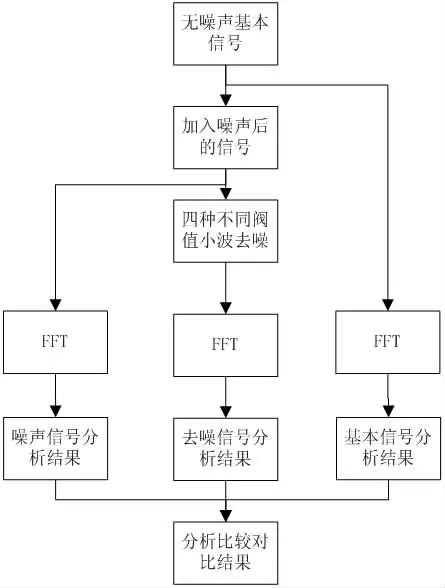
1 实验流程图

仿真实验步骤：

（1）设定原始信号，叠加白噪声。

（2）使用4种阀值分别对加噪信号进行小波去噪处理，并与原信号进行波形对比。

（3）对原信号、加噪信号、去噪后信号进行FFT处理，输出幅值图对比。

（4）变换白噪声幅值、小波去噪分解层数，多次实验，观察其变化情况。

（5）分析比对各项结果，得出结论。

仿真实验结果：

原始信号：

叠加的噪声信号：

使用MATLAB小波工具箱进行去噪处理，采用其自带的sym8小波基，进行5层小波分解用于去噪。

图2 叠加较高噪声时各信号波形图

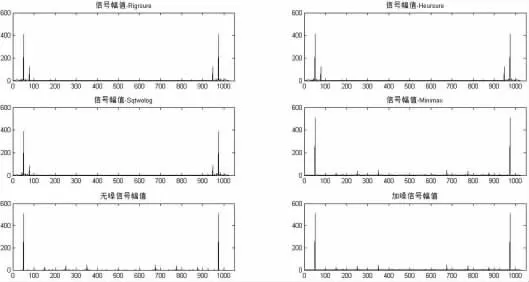
图3 叠加较高噪声时各信号幅值图

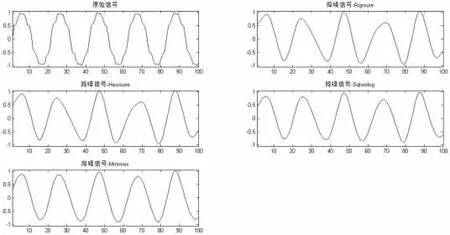
图4 叠加较低噪声时各信号波形图

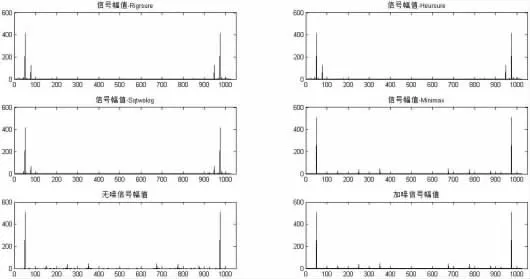
图5 叠加较低噪声时各信号幅值图

观察波形、幅值图可知，去噪前，波形中存在大量的非整次谐波，严重干扰对各次谐波的检测，而在运用四种不同的阀值小波进行去噪后，虽然各自在不同程度上都对波形造成了一定的影响，但均能在一定程度上提高对谐波检测的精度。去除了加噪信号中大量的非整次谐波影响，在一定程度上提升了检测效果。

减少小波分解层数：（lev=2）

图6 降低小波分解次数后，叠加较高噪声时各信号波形图

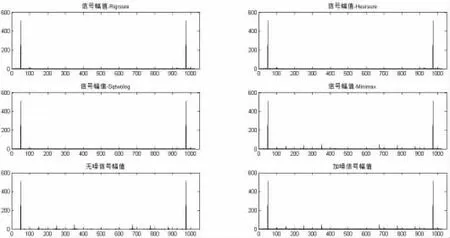
图7 降低小波分解次数后，叠加较高噪声时各信号幅值图

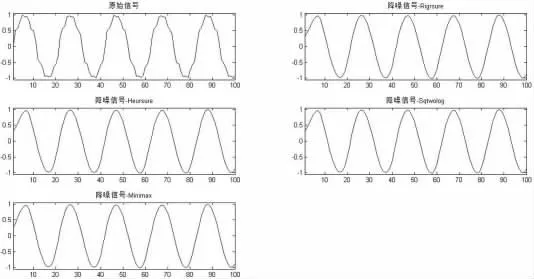
图8 降低小波分解次数后，叠加较低噪声时各信号波形图

图9 降低小波分解次数后，叠加较低噪声时各信号幅值图

在降低小波分解层数，即探讨对波形影响能否降低：

经对比图2与图6、图4与图8：当小波分解层数减少时，会降低其对波形的影响；对比图 3与图7、图5与图9：当小波分解层数减少时，谐波检测去除的干扰量也有所减少（如存在有大量非整次谐波）。

4 结论

本文通过在对FFT和小波分析等谐波分析方法进行研究比较的基础上，探究一种融合FFT和小波变换法的谐波分析法的可行性。在综合辨析了FFT和小波理论后，讨论了FFT和小波分析法的优缺点，并尝试先借助小波的特性剔除了信号中的大部分噪音，再进行FFT分析。仿真实验结果验证，结合FFT和小波分析对电力谐波的检测，能在一定程度上提高对谐波检测的精度和实时性，并通过探讨多种阀值处理和不同层数小波分解，了解其存在应用到实践中的可行性。

[1]陈磊.电弧炉电气系统的建模与谐波分析[D].沈阳：东北大学电气工程学院,2008.

[2]张向程.基于小波变换的电力谐波参数测量方法研究[D].长沙：湖南大学电气工程学院,2004.

[3]刘艳利.电力系统谐波检测算法研究与实现[D].威海：山东大学电气工程学院,2012.

[4]李益华.电力系统谐波检测的FFT加窗插值算法与小波分析方法的比较[J].电力科学与技术学报，2007，22(2):39-42.

[5]胡晓冬，董辰辉.MATLAB从入门到精通[M].北京:人民邮电出版社，2012.

[6]高成.Matlab小波分析与应用[M].2版.北京:国防工业出版社，2007.

[7]孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.

[8]胡昌华，张军波，夏军，等.基于MATLAB的系统分析与设计(小波分析)[M].西安:西安电子科技大学出版社，1999：217-225.

[9]吴竞昌.供电系统谐波[M].北京:中国电力出版社，1998.

[责任编辑：桂传友]

TM711

A

1674-1102(2014)06-0044-04

10.13420/j.cnki.jczu.2014.06.012

2014-03-04

童晋（1991－），男，安徽池州人，合肥工业大学电气工程学院硕士研究生，研究方向为电气工程。