大型汽轮机高压进汽阀启动过程换热规律研究

陈永照， 黄 威， 王宇翔， 刘丽平， 忻建华

（1.上海交通大学 动力机械与工程教育部重点实验室，上海200240；2.上海电气电站设备有限公司，上海200240）

随着汽轮机技术的不断发展，运行参数不断提高，运行方式逐渐多样化，机组中各部件的换热情况越来越复杂.一些高温下运行的厚壁部件在机组启动和变工况过程中容易受热不均，产生较大的内部热应力，如果热应力控制不当，则直接影响机组安全性和役期内的寿命.目前，国内外针对高中压汽缸、转子等部件在启动和稳定运行时的热应力进行了较多的研究，并将其作为控制机组启停和变负荷速率的依据之一［1－3］，而对于同属高温厚壁部件的高压进汽阀，相关资料还比较匮乏.阀门启停过程热应力的计算与启停各阶段的传热系数有关，传热系数直接影响热应力分析的正确与否.笔者以某超超临界百万机组的高压进汽阀为例，通过计算和试验比较的方法，分析机组启动过程中主调阀门的换热特性，得到了启动和稳定运行的传热系数，为后续阀门热应力的研究和控制提供依据.

1 启动过程换热分析

现代先进汽轮机主调阀的结构是将主蒸汽阀（以下简称主阀）和调节阀整合为一体直接安装到高压缸上，结构示意图见图1.这种形式的主阀和调节阀紧密相连，结构紧凑，压损较小，但国内缺少对其启停过程中换热规律的研究资料.图1中，蒸汽从主阀进口管道A进入主阀腔室B，在主阀阀门开启状态下经主阀和调节阀之间的连通管道进入调节阀腔室C，最后经调节阀出口管道D进入高压缸.

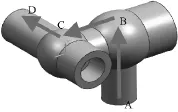
图1 某超超临界机组高压进汽阀结构示意图Fig.1 Structural diagram of a USC HP valve

汽轮机组的启动根据部件的初始金属温度不同分为冷态、温态、热态和极热态4种方式，其中冷态启动时阀门换热情况最复杂，阀门的热应力也最大，因此工程设计上可用冷态启动过程来涵盖另外3种启动过程.笔者通过研究冷态启动的传热过程以得到高压主调阀的换热规律.

图2为机组实际冷态启动过程曲线.图中A时刻表示锅炉点火开始启动，此时主阀和调节阀均为关闭状态.但锅炉一旦产生蒸汽（蒸汽温度110℃、压力0.137MPa）即沿主蒸汽管道进入主阀腔室，开始预暖主蒸汽管道和主阀，此时蒸汽在管道内表面和主阀腔室壁面发生凝结换热.随着蒸汽参数不断提高，主阀内壁金属温度（主壁温）也不断升高，但均低于主蒸汽压力下对应的饱和温度.此期间的高强度凝结换热使主阀内壁金属温度快速上升，并保持与蒸汽压力下的饱和温度（汽饱温）之间有一较小的温差但又与饱和温度变化趋势一致，直到图中B时刻二者温度基本一致，凝结换热结束，此时主阀内壁金属温度达282.7℃，蒸汽温度为498.7℃、压力为6.69MPa.此后主阀进入对流换热阶段.

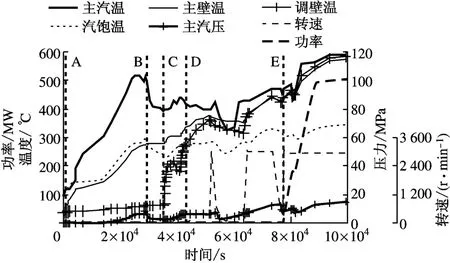
图2 某超超临界机组冷态启动过程曲线Fig.2 Cold start－up curve of the USC unit

图2中C时刻预暖管道和预暖主阀基本完成，主阀阀门打开，蒸汽进入调节阀腔室开始预暖调节阀.同样，调节阀金属壁面先与蒸汽发生凝结换热，在D时刻进入单相对流换热阶段.在凝结换热初期调节阀金属温度（调壁温）几乎呈阶跃上升，最大温升速率达33.2K／min，这主要是由于主阀开启瞬间调节阀腔室内蒸汽压力突升，蒸汽饱和温度相应升高，对调节阀的金属表面形成热冲击所致.

D时刻结束预暖调节阀，调节阀阀门微开，蒸汽进入高压缸预暖转子和内缸.此后在调节阀控制下进行了3次冲转，E时刻成功并网带负荷，然后进入升负荷和稳定运行阶段.

整个启动过程中，阀门温度状态的差异、蒸汽参数的波动以及流量的变化导致高压进汽阀内换热情况复杂，主阀和调节阀均先后经历凝结换热和单相对流换热.凝结换热阶段换热强度受蒸汽压力影响明显，单相对流主要受蒸汽温度和流量影响.

2 传热系数计算

由第1节分析可知，阀门冷态启动过程经历了凝结和单相对流2个换热阶段.目前，国内外关于阀门内换热规律的研究很少.传热系数多采用平板或圆管公式再考虑修正系数来计算.

凝结过程由于换热剧烈，部分文献将其作为第一类边界条件，或取传热系数为一较大的定值［4］，这种处理方法忽略了蒸汽凝结产生液膜的热阻以及凝结过程中液膜厚度的变化.考虑实际情况，可以分别选取努塞尔凝结换热分析解中的竖壁、球面和柱面公式，来计算主阀进口管道、主阀和调节阀腔室、主阀和调节阀的连通管道和调节阀出口管道的凝结传热系数，计算公式如下

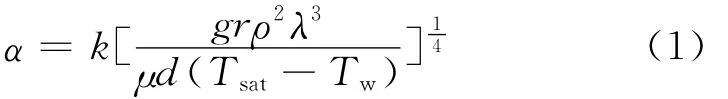
式中：系数k对应于球面、竖壁及柱面分别为0.826、1.13和0.729；ρ为饱和水的密度，kg／m3；λ为导热系数，W／（m·K）；μ为动力黏性系数，Pa·s；r为潜热，J／kg；Tsat和Tw分别为蒸汽压力下的饱和温度和金属壁面温度，℃；d为特征尺寸，m.

对于单相对流换热，有学者研究得到2类计算传热系数的经验公式.第一类公式为努塞尔数准则公式，如文献［5］和文献［6］所用分别以阀门入口管道直径和管中流速作为特征尺寸和速度的准则公式

式中：阀腔部分系数k1＝0.046；阀腔进、出口管道系数k1＝0.021.

对管道的弯曲部位应加以修正

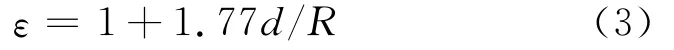
式中：d和R分别为管道直径和弯曲部位的曲率半径.

第二类公式是根据能量平衡方程利用实测数据计算传热系数，如热平衡法［7］.

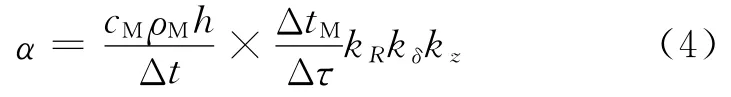
式中：cM、ρM分别为金属比热容和密度，J／（kg·K），kg／m3；h为金属壁厚，m；Δt为 Δτ时间内蒸汽与壁面平均温差，K，ΔtM为Δτ时间内金属平均温度变化值，K；kR和kz分别为考虑了壁面曲率和轴向导热的修正系数，kR＝1＋h／2R；kδ为壁面真实温度与距壁面δ处温度测点间的温差修正系数.

当温度沿壁厚呈抛物线分布时，

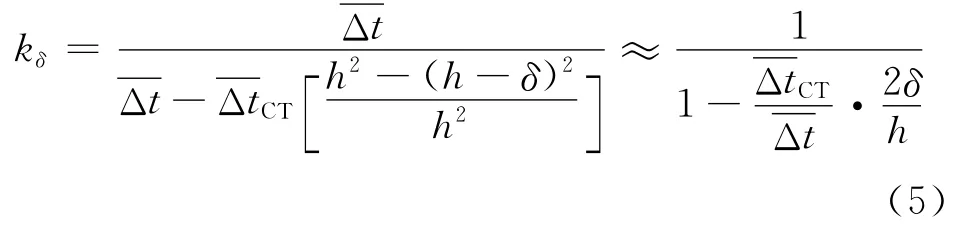
式中：ΔtCT为Δτ时间内沿壁厚平均温差.

经实际应用发现，上述公式均存在一定的局限性.如式（2）由于缺少阀门启动各时刻的准确流动参数而无法使用，式（4）对于结构复杂的阀门难以确定轴向导热修正系数，另外由于各种类型阀门的结构差异较大，计算所得传热系数也存在较大误差.

笔者根据实际情况，提出了确定传热系数的新方法——逐步逼近法.采用试验和理论计算相结合的方法，并借助有限元分析软件，利用迭代和修正传热系数计算温度场，使各测点的温度计算值与测量值吻合，最终得到传热系数.具体步骤如下：首先将整个启动过程按阀门内的流动特点［8］分为若干计算时段，认为各时段内传热系数是常数或按线性变化.然后确定各时段传热系数迭代初始值.为了减少迭代次数和缩短计算时间，方便对现有传热系数计算方法的精度和适用性进行比较和评价，选用图2所示的实际启动曲线和相应的热力参数，利用式（1）和式（4）计算所得凝结换热阶段和单相对流阶段的传热系数作为迭代初始值，部分时段传热系数计算结果见表1.考虑到凝结传热系数与凝结水膜厚度直接相关，而水膜厚度主要受温差ΔT＝Tsat－Tw的影响，所以表中凝结换热时段大致按ΔT值划分，表2类似.

表1 经验公式计算所得传热系数Tab.1 Heat－transfer coefficient calculated by empirical formula W／（m2·K）

根据图2的启动曲线和表1的传热系数，利用有限元计算软件对阀门进行了三维非稳态的温度场计算.图3为在整个启动过程中主阀计算温度和实测温度的比较.从图3可以看出，采用上述公式计算所得温度在大部分时段内与实测值变化趋势一致，但在升速、升负荷等过渡工况时偏差较大，最大偏差为56.8K，平均偏差为26.6K.

之后依据计算温度和实测温度的偏差对各阶段的传热系数进行逐步修正.引入修正系数k2，则修正过程可表示为

式中：αi、αi＋1分别为修正前、后的传热系数；Ts为加载温度；Tw，i为αi计算的内壁面温度.

用式（6）进行逐步逼近若干次传热系数修正和温度场计算，若计算结果Tw，i与实测值Tw之差小于某一设定值（设定值主要由其对应力计算结果的影响程度确定，应确保在设定值范围内应力计算结果不会有较大偏差），认为此时传热系数已充分逼近真实值，则停止逐步逼近修正过程.图3给出了本例中经过3次传热系数修正后主阀计算温度和实测温度的差异，可以发现二者几乎完全重合.进一步数据分析表明，二者最大温度偏差为7.2K，平均温度偏差为3.2K，此时应力计算偏差为4.8%，满足工程设计的要求.传热系数部分计算结果见表2.

从上述对2种传热系数计算方法的介绍和计算结果的比较分析可以看出，经验公式计算过程简单，但结果准确度不够；而逐步逼近法实用性强，虽然计算量稍大，但精度很高.因此，在实际应用中，对于较为粗略的分析，可以直接选用式（1）～式（4）计算传热系数，而对于要求较高的精确计算，可以在公式计算基础上采用逐步逼近法进行修正，直至达到精度要求.

表2 逐步逼近法计算所得传热系数Tab.2 Heat－transfer coefficient calculated by step－by－step approach W／（m2·K）

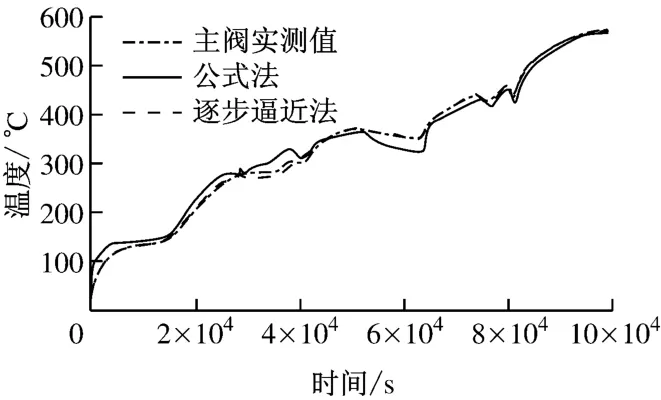
图3 主阀温度实测值与计算值的比较Fig.3 Comparison of main valve temperature between calculated results and actual measurements

3 传热系数适用性研究

逐步逼近法计算传热系数必须建立在一定的试验数据基础上，但在新阀门设计阶段，往往缺少相应的试验数据，因此要获得精确的传热系数是困难的，只能根据经验选取.针对这种情况需要进一步研究传热系数对于不同阀门的适用特点.

首先研究结构形式相同的阀门传热系数的适用性.图4为另一组主调节阀的冷态启动过程曲线，该启动过程与图2中基本一致，依次为暖主阀、暖调节阀、暖机、冲转并网、升负荷和稳定运行，且阀门结构也基本相同.

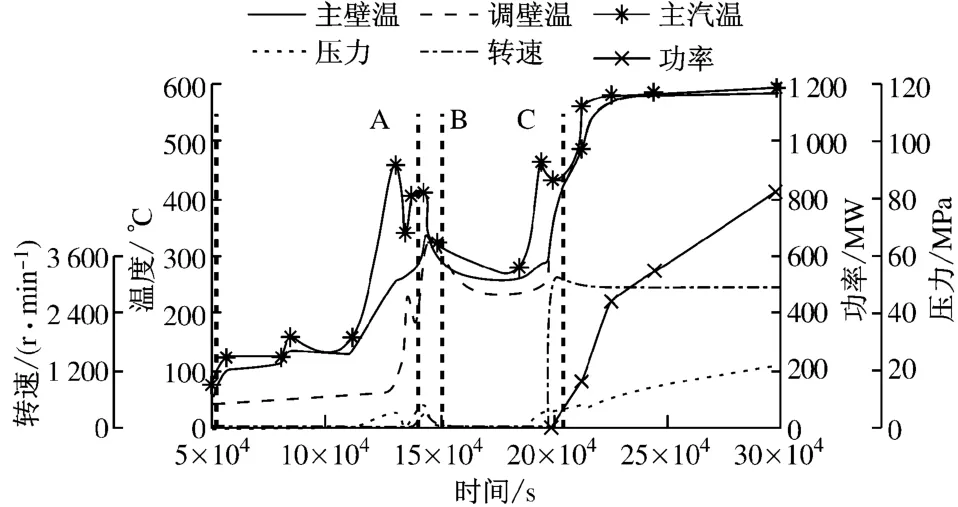
图4 另一超超临界机组冷态启动过程曲线Fig.4 Cold start－up curve of another USC unit

将前面逐步逼近法所得各阶段传热系数的选取规律（见表2）直接应用于这一启动过程计算，并将计算温度与实测值进行比较（见图5），发现除了某些特殊时刻，如阀门突然开启、关闭等，绝大部分时段的计算结果与实测值能很好地吻合，最大温度偏差为16.9K，平均温度偏差为5.7K，证明逐步逼近法所得传热系数对结构基本相同的阀门是适用的，这为不同蒸汽参数和容量的新阀门的热强度设计、非稳态运行工况热应力的计算和控制提供了依据.

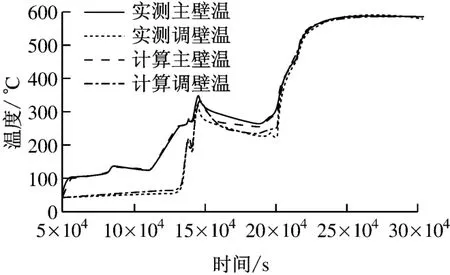
图5 传热系数用于同类阀门时计算值与实测值的比较Fig.5 Comparison between actual measurements and calculated results with heat－transfer coefficient applied to same type of valves

然后研究不同型号阀门沿用传热系数的规律.图6为某超临界600MW机组高压进汽阀的结构示意图，其中A为主阀，B和C为调节阀，与图1中阀门的差异较大.

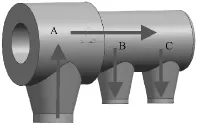
图6 某超临界机组高压进汽阀结构示意图Fig.6 Structural diagram of an SC HP valve

图7为该机组的冷态启动过程曲线，阀门所经历的启动阶段与前述超超临界机组基本相同，主要区别在于主阀阀门打开前调节阀已处于开启状态，因此开启主阀之后暖调节阀与暖机同时进行.将表2中的传热系数选取规律直接应用于该机组阀门，计算启动过程的温度分布，并将计算结果与实际数据进行比较，结果见图8.从图8可以看出，在整个启动过程中，计算所得主阀和调节阀内壁温度与实测值变化趋势一致，在C区计算值与实测值的偏差较小，但在主阀凝结换热前期（A1区）和调节阀凝结换热阶段（A2和B区）计算结果明显偏高（最大温度偏差为33.6K），表明这些时段的传热系数比实测值偏大.这说明阀门结构和运行方式对传热系数影响较大.

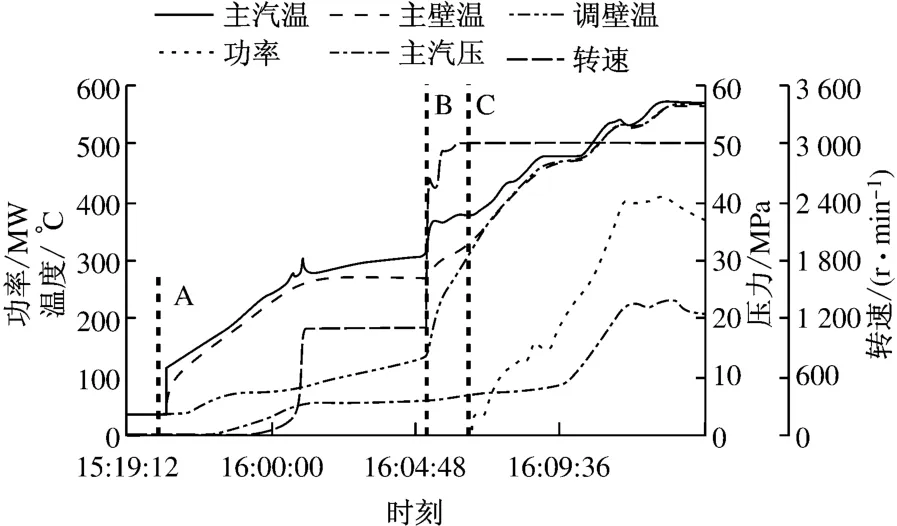
图7 超临界机组冷态启动过程曲线Fig.7 Cold start－up curve of the SC unit

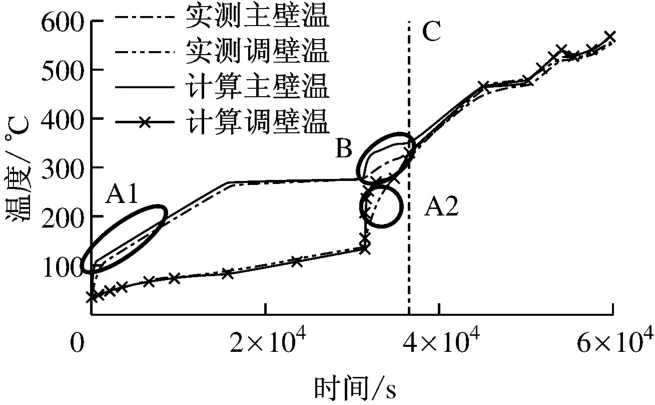
图8 传热系数用于非同类阀门时计算值与实测值的比较Fig.8 Comparison between actual measurements and calculated results with heat－transfer coefficient applied to different types of valves

对比图1中超超临界机组的阀门，在暖调节阀阶段主阀阀门开度较大，调节阀腔室内压力和流量较大，换热强度较高；而图6超临界机组的阀门暖调节阀和暖机同时进行，主阀阀门需要控制转子转速和暖机过程，因此开度很小（2%左右），调节阀腔室内的压力低、流量小，换热强度也相对较低，传热系数更小.若要得到这些时段的真实传热系数，需要采用逐步逼近法进一步计算.总体而言，不同结构的阀门间传热系数直接应用会因机组运行方式及阀门结构的不同产生一定的计算偏差，但可以满足工程中粗略计算的要求，具有一定的借鉴意义.因此，在设计不同于图1所示的阀门结构时，可以用表2所示的阀门在不同阶段的传热系数进行热强度设计和启停过程的热应力控制，在阀门投入运行后，根据阀门的实测数据采用逐步逼近法求得更为精确的传热系数，对阀门的热应力控制过程进行修正，以保证阀门在役期内的安全.

总结传热系数在不同阀门间的适用特点发现，对于结构基本相同的阀门，若机组运行方式相同，则传热系数是直接适用的，计算产生的偏差较小；而当结构不同、机组运行方式存在一定差异时，为满足较高精度的计算要求，阀门传热系数应根据实际运行方式差异进行适当修正.

4 结 论

（1）机组冷态启动时高压进汽阀内换热情况复杂，阀门各部位与蒸汽均先后进行凝结换热和单相对流换热，为避免热冲击，凝结换热阶段应限制蒸汽的压力，单相对流换热阶段则要控制蒸汽温度和流量.

（2）总结当前文献提供的阀门传热系数计算公式，并根据实际情况提出逐步逼近法.在实际计算中比较二者的计算效果，发现公式法因实际情况的复杂性存在一定的偏差，而逐步逼近法计算所得传热系数具有较高的可信度.

（3）对阀门传热系数适用性的研究发现，相同结构和运行方式的阀门间传热系数可以通用，不同结构和运行方式的阀门间传热系数直接应用会在某些时段产生一定的偏差，但整体效果良好.这为传热系数的简化计算和相互借用提供了重要依据，所得传热系数选取规律也可推广应用.

（4）对于获取传热系数的方法，建议在有实际运行数据时，根据式（1）～式（4）初步计算，若要准确计算，可在逐步逼近法的基础上进行适当修正；在没有实测数据的情况下，比如新阀门的设计，可以直接选用本文提供的传热系数，其计算结果满足近似计算要求.

［1］支小牧，寇可新，曹向欣.汽轮机转子热应力在线监测、寿命管理及优化启动的研究［J］.动力工程，2000，20（1）：543－548.ZHI Xiaomu，KOU Kexin，CAO Xiangxin.Steam turbine rotor thermal stress on－line supervision，life management and optimal start－up study［J］.Power Engineering，2000，20（1）：543－548.

［2］郑李鹏，陈坚红，盛德仁，等.燃气－蒸汽联合循环汽轮机快速启动的研究［J］.动力工程学报，2011，31（8）：579－584.ZHENG Lipeng，CHEN Jianhong，SHENG Deren，et al.Study on quick start up of steam turbine in a gassteam combined cycle［J］.Journal of Chinese Society of Power Engineering，2011，31（8）：579－584.

［3］方宁，纪冬梅，姚秀平，等.基于径向基函数神经网络的汽轮机转子等效应力计算模型［J］.动力工程学报，2011，31（4）：268－272.FANG Ning，JI Dongmei，YAO Xiuping，et al.Computation model for equivalent stresses in steam turbine rotors based on RBF neural network［J］.Journal of Chinese Society of Power Engineering，2011，31（4）：268－272.

［4］王宏光，戴韧，刘岩，等.超临界汽轮机阀壳的温度场和应力场计算分析［J］.上海理工大学学报，2007，29（1）：75－78.WANG Hongguang，DAI Ren，LIU Yan，et al.Numerical analysis of temperature and stress field in valve housing of super critical steam turbine［J］.Journal of University of Shanghai for Science and Technology，2007，29（1）：75－78.

［5］彭震中，丁祝顺，王璋奇，等.汽机调节阀阀体三维瞬态温度场及应力场分析［J］.热能动力工程，2002，17（1）：81－83.PENG Zhenzhong，DING Zhushun，WANG Zhangqi，et al.Numerical analysis of temperature and stress field in control valve housing of a steam turbine［J］.Journal of Engineering for Thermal Energy and Power，2002，17（1）：81－83.

［6］李德生，荆建平，孟光.汽机阀壳瞬态温度场及应力场仿真分析［J］.汽轮机技术，2008，50（1）：6－8.LI Desheng，JING Jianping，MENG Guang.Numerical simulation of temperature field and stress field of the valve box of a steam turbine［J］.Turbine Technology，2008，50（1）：6－8.

［7］普罗特金，列依泽罗维奇.单元发电机组汽轮机启动工况［M］.夏同棠，译.北京：水利电力出版社，1985：48－52.

［8］朱奇，谷传纲，戴韧.超超临界百万千瓦汽轮机主调节阀流场非稳态数值研究［J］.动力工程学报，2010，30（10）：743－748.ZHU Qi，GU Chuangang，DAI Ren.Numerical simulation on unsteady flow field in the main stop and control valve system of a 1 000MW ultra－supercritical steam turbine［J］.Journal of Chinese Society of Power Engineering，2010，30（10）：743－748.