基于线阵CCD的电子白板技术研究

骆力，谌小跞，井梦曦

(1.安徽工业大学计算机科学与技术学院，安徽马鞍山243032；2.深圳市海亚科技发展有限公司，广东深圳518000)

基于线阵CCD的电子白板技术研究

骆力1，谌小跞2，井梦曦2

(1.安徽工业大学计算机科学与技术学院，安徽马鞍山243032；2.深圳市海亚科技发展有限公司，广东深圳518000)

基于线阵CCD技术的交互式电子白板由于其低成本及可高效率地实现多点触控，展现出较大的发展潜力。针对采用线阵CCD技术的电子白板普遍存在的伪触摸点问题，在动态建模基础上分别采用扩展Kalman滤波算法和粒子滤波算法解决触摸点目标跟踪问题。结果表明，与传统的扩展卡尔曼滤波算法相比，粒子滤波算法提高了目标跟踪的精度，更好地解决了伪点问题。该研究结果可为交互式电子白板的设计方法提供理论依据和技术支持。

电子白板；线阵CCD；扩展卡尔曼滤波算法；粒子滤波算法

交互式电子白板主要应用于多媒体教学与会议，它通过触摸图形化界面的方式实现对应用程序的操作[1]。现阶段市场上可以实现交互式电子白板精确定位的主要技术有:电磁感应、红外感应、电阻压感、超声波和CCD扫描等技术。从国内外文献来看，能较好实现多点触控的交互式电子白板都具有技术复杂、体积较大的缺点，如纽约大学媒体研究室提出的基于面阵CCD后视和受抑全内反射（FTIR）的设计[2]。相比于文献[2]提出的方案，国外几家老牌电子白板生产商如SMARTTechnologies,Lum io和NextWindow相继采用的基于线阵CCD侧视的电子白板设计方案具有成本低、体积小等优点。该技术的工作原理是用线阵CCD检测电子白板表面的图像，通过对图像的处理计算，得到触摸点的位置，但难以实现多点触控[3]，其主要的技术困难是伪触摸点问题。伪触摸点的产生是由于线阵CCD不能获得触摸点的深度信息，从而对触摸点的数量判断错误。本文研究基于扩展卡尔曼滤波器与粒子滤波器的目标跟踪方法在电子白板中的应用，为设计实现多点触控的电子白板提供理论依据。

1 基于线阵CCD电子白板的原理与伪点问题

基于线阵CCD的电子白板结构如图1所示，白板上端左右2个顶点各有1块光学检测模组，白板的周围铺设有自回归反射膜。每块光学检测模组由一个激光扫描单元和一个线阵CCD组成，激光扫描单元发射不同角度的光线，通过自回归反射膜回到线阵CCD，线阵CCD根据光线强度产生不同强度的模拟信号。当手指触摸到电子白板上时，经过触摸点的光线就被阻挡，线阵CCD就会在相应的像敏单元产生较低的模拟信号。这样线阵CCD就可以检测到触摸点的方向。由2个线阵CCD检测到的方向可以计算出触摸点的位置。但是由于触摸点的相互遮挡和干扰，会出现盲区和伪触摸点的问题。盲区由于触摸点相互遮挡产生，电子白板对触摸点发生漏检，盲区的影响不严重，因为漏检的触摸点通常很快会被检测到，对操作者来说仅会感觉系统的响应稍有延迟。相比于盲区，伪触摸点的影响较大，触摸点会出现在其本不该出现的地方，发生误操作。以图1为例，A点和B点为真实触摸点，每个真实触摸点都会被2个线阵CCD分别检测到，这样共有4个方向的光束被真实触摸点遮挡，这4个方向可能会出现另外2个交叉点C和D。电子白板可能会将C和D认为是真实触摸点。

采用目标跟踪算法可以有效解决伪点问题。系统根据触摸点当前的状态估计触摸点下一时刻的状态，当下一时刻观测到的触摸点与估计的触摸点位置相差较远时，系统认为有2种情况：(1)如果观测到的触摸点在下一帧观测数据中消失，系统将观测数据判定为伪点。(2)如果观测到的触摸点在下一帧观测数据中仍然存在，系统将该点判定为新触摸点，并对该点进行跟踪[4]。衡量目标跟踪算法对触摸点轨迹估计性能的指标主要有程序运行时间、误差的均值、和误差的方差。

2 动态目标建模

由于线阵CCD的扫描频率通常大于1000帧/s，可以认为在线阵CCD得到2帧图像之间的时间段，触摸点为匀速，因此对触摸点的状态建立模型如式(1)，触摸点的状态向量共包括4个参数：触摸点的x坐标、触摸点的y坐标；触摸点在x方向上的速度、触摸点在y方向上的速度。

目标的状态序列{xk,k∈N}可以表示为

其中fk:Rnx×Rnv→Rnx是一个和xk-1,{} vk-1,k∈N有关的非线性方程。过程噪声序列为vk，nx和nv分别是状态的维数和过程噪声向量。N是自然数集。被追踪的触摸点状态xk可以从包含噪声的观测结果zk中估计。

由于在电子白板中通常采用鱼眼镜头的线阵CCD，观测函数为非线性函数，因此hk:Rnz×Rnn→Rnz是一个非线性方程。nk是观测噪声序列，nz和nn分别是测量矩阵的维数和测量矩阵的噪声向量。需要特别指出的是，寻找的xk的滤波估计是基于从时间1一直到时间k所有可观测的结果。

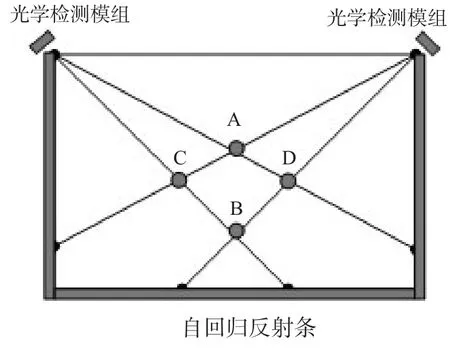
图1 伪触摸点问题Fig.1 Pseudo touch point

3 扩展Kalman滤波算法

在动态系统中，目标跟踪可以归结为状态估计问题，即从观测系统来估计动态系统的真实状态，如果当前的状态值是由当前及过去的观测值来估计，则称之为预测[5]。卡尔曼滤波器算法是目前目标跟踪中广泛使用的方法，通过构造先验估计，并在下一时刻根据带噪声量测结果获得反馈，成为结合先验估计和更新的测量结果的后验估计。因此，卡尔曼滤波器的计算可以分为2个部分：时间更新部分和状态更新部分。时间更新部分负责根据运动物体现在时间点的状态向量，来估计下一个时间点的状态向量和误差的协方差。状态更新部分负责根据量测结果反馈，并校正先前的估计情况。

标准卡尔曼滤波器要求目标的观测矩阵和运动描述矩阵都是线性的，而线阵CCD关于触摸点的观测矩阵是非线性的。因此，在工程上通常需要做某种近似即寻找上述问题的次优解[6]。使用最多的次优算法即是扩展卡尔曼滤波(EKF：extended KF)。扩展卡尔曼滤波器解决非线性关系的方法是将期望和方差线性化。同泰勒级数类似，面对非线性关系时，扩展卡尔曼滤波器通过求状态方程和量测方程的偏导以得到线性化的表达式并计算当前估计。即将非线性关系线性截断，从而将其近似描述出来。

扩展卡尔曼滤波算法可以表现为下面的递归关系，变量定义与卡尔曼滤波器算法公式相同。式中x̂-k是预估的状态向量，A是状态转移的过程矩阵，uk-1是允许外部控制施加于系统的变量，P-k是预估的误差协方差矩阵，Q是过程噪声矩阵，H均表示观测矩阵，R是观测噪声矩阵，K是卡尔曼增益。为了描述非线性的过程关系和观测关系，用过程函数f代替标准卡尔曼滤波中的过程矩阵A，用观测函数h代替标准卡尔曼滤波器中的观测矩阵H。W是过程函数f的雅克比矩阵，V是观测函数h的雅克比矩阵。

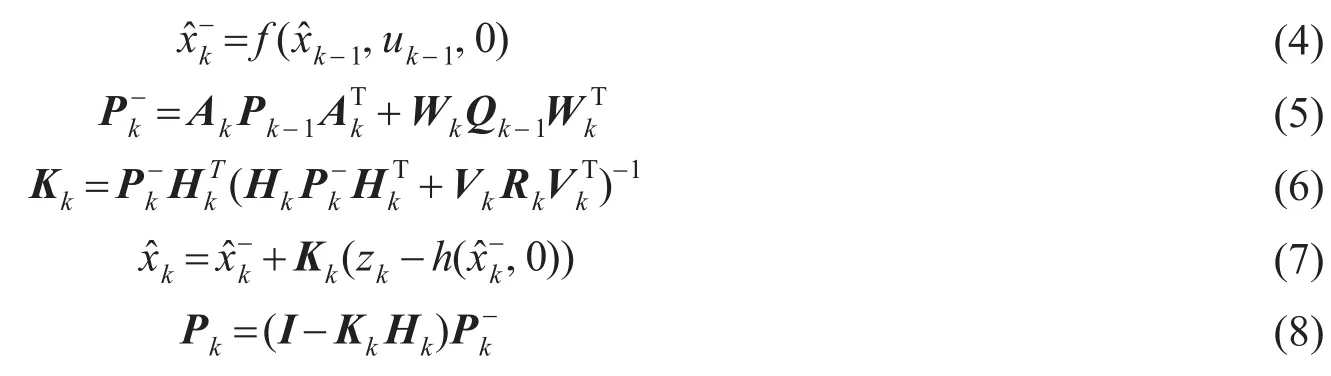
由于实际非线性动态模型较复杂,存在不确定性或噪声统计特性近似已知或未知,造成了滤波器性能下降[7]。因此滤波估计技术在实际应用时,扩展卡尔曼滤波器的收敛性、估计精度、实用性需要验证。

为了验证EKF算法的性能，通过下面的例子进行仿真分析。采用符合上文描述的马尔科夫过程的样本点，即系统的当前状态变量仅与其前一时刻的状态变量有关。数学模型如下:

其中：wk是过程噪声，服从伽马分布；vk是量测噪声，服从N(0,0.1)的高斯分布。跟踪50个随机采样点，进行100次独立实验。仿真过程中扩展卡尔曼滤波算法的均方误差的均值为0.379 1，均方误差的方差为0.175 2，平均运行时间为0.044 8 s。单次仿真结果见图2。从仿真结果可以看出采用扩展卡尔曼滤波算法，误差的方差较大，说明该算法在稳定性上存在不足。因此本文提出采用粒子滤波算法进行触摸点的目标跟踪。

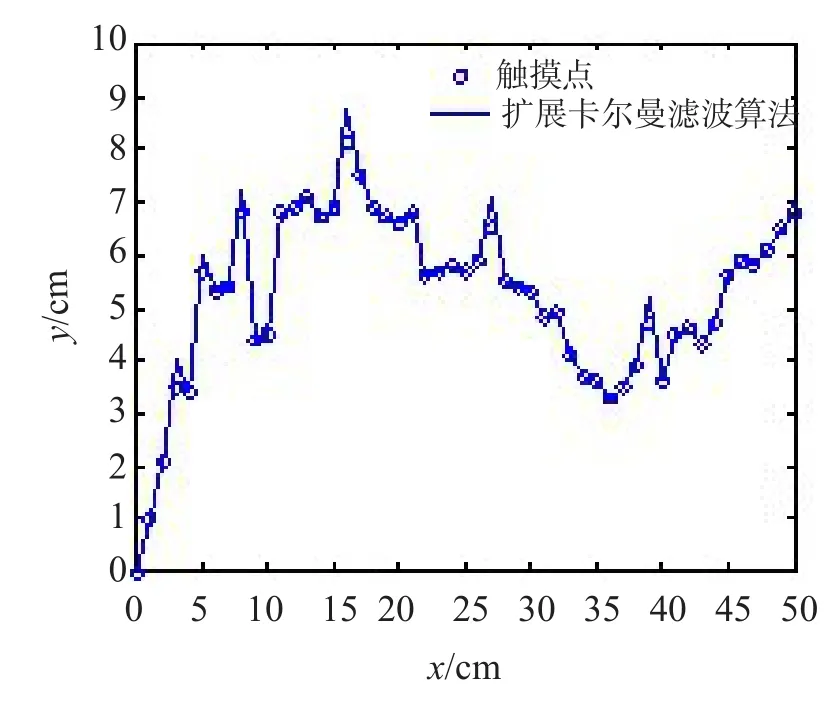
图2 扩展Kalman滤波跟踪Fig.2 EKF tracking algorithm

4 粒子滤波算法

从贝叶斯的角度看，电子白板动态系统中的递归状态xk根据量测结果z1:k估算得出，z1:k是时间从1到k观察到的数据。因此，需要构建概率密度函数p(xk|z1:k)。假设初始状态向量的概率密度函数是p(x0|z0)≡p(x0)，并且是事先已知可用的。在原则上，这个概率密度函数p(xk|z1:k)可以递归得到，递归的过程分为2个阶段：预测和更新。

假设要求的概率密度函数p(xk-1|z1:k-1)在时间k-1是能得到的。在预测阶段，包括使用马尔科夫方程来获得之后的在时间k的状态的概率密度函数为

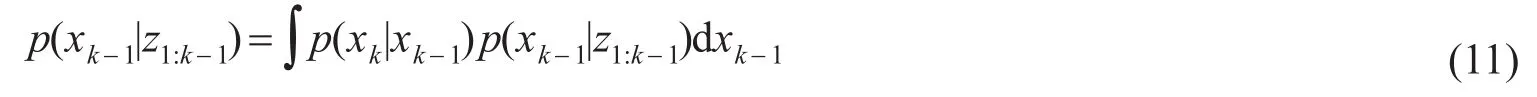
在上式中，p(xk-1|z1:k-1)kk-1被描述成一个马尔科夫过程。这个关于状态序列p(xk|xk-1)的概率模型由下面的系统方程定义，其中vk-1为过程噪声向量。

在时间k，可以获得一个量测结果zk，那么这个量测结果就可以用来被更新现在的状态。依照贝叶斯准，则有

这种后验概率密度的递归推广仅是一般概念的解决方案，而不能解析地确定。因此，包括卡尔曼滤波器和基于网格的滤波器解决方案在计算时存在受到限制的情况。为改善该解决方案，采用近似最佳逼近的贝叶斯解决方案——粒子滤波器。

粒子滤波算法实际就是采用蒙特卡罗方法来求解递推的Bayes滤波问题。而蒙特卡罗方法的核心是将积分问题转化为有限样本点的概率转移累加过程，如果可以从p(x0:k|z1:k)中抽取N个独立同分布的样本点，则可将每个粒子赋予l/N的权值[8]。但实际中抽样过程比较困难，常常需要借助于采样算法，本文采用重要性采样算法（SIS）。

权重选择使用重要性抽样原则。假设难以得出样本的概率密度函数，但它可以被估计。另设xi=q(x)成为一个容易从q(x)中产生的样本，即成为重要密度采样。加权近似密度由下式给出

其中

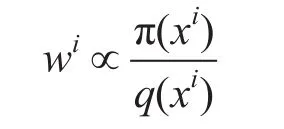
是对第i个粒子的归一化权重。

为了比较粒子滤波算法和扩展卡尔曼滤波算法的性能，使用3中相同的例子进行仿真分析。对50个采样点进行跟踪，进行100次独立实验，得到的单次仿真结果见图3。

图3为一次粒子滤波算法在一次独立实验中产生的状态估计曲线。仿真过程中粒子滤波算法的均方误差的均值为0.280 5，均方误差的方差为0.092 3，平均运行时间为0.087 7 s。在误差均值和方差方面，粒子滤波算法均优于EKF算法。由图3可以看出，该算法对非线性部分有很好的跟踪性能。在实际工程中，电子白板应对每个触摸点分别构造跟踪器，均方误差较小，意味着触摸点有较小的概率出现互相干扰的情况。如果均方误差较大，当2个或多个触摸点距离较近时，跟踪器可能丢失原本跟踪的触摸点，而开始对其他的触摸点进行跟踪。由此可以看出粒子滤波算法具有较小的均方误差，可以使电子白板在工作中具有更稳定的性能。如果采用50帧/s的线阵CCD摄像器件，每秒可以采集到50个更新的触摸点观测数据，由程序的运行时间看出对50个触摸点观测数据进行滤波处理需要0.44 s，这样的运行时间完全可以满足使用要求。

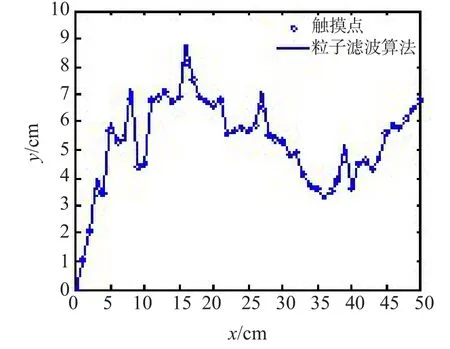
图3 粒子滤波跟踪Fig.3 PF tracking algorithm

应用了粒子滤波方法以后，在电子白板上进行书写，虽然误差达到要求，但可能会出现毛刺。因此需要在每写一笔后，对该笔划进行平滑校正。本文使用的平滑方法是移动平均方法，计算机仿真表明，滑窗的长度越长，平滑效果越好，但向书写方向滞后越严重。采用滑窗大小为5个触摸点观测数据，滑窗滤波算法结果仿真见图4。

5 结语

基于CCD技术的电子白板因其低成本、高效率地实现多点触控，具有广阔的应用前景。本文指出线阵CCD技术的伪点问题，并研究基于粒子滤波器的目标跟踪算法在电子白板中的应用。与传统的卡尔曼滤波和扩展卡尔曼滤波算法相比，该方法的精度优于后者，可以更好地解决了伪点问题。

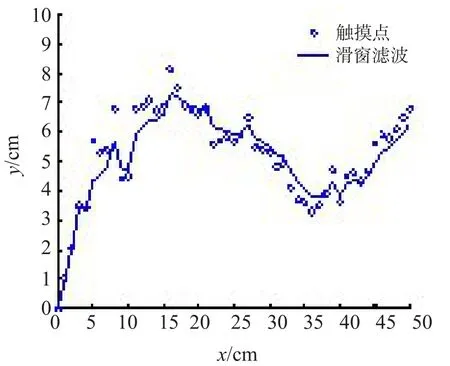
图4 滑窗滤波Fig.4 Slidingw indow filter

[1]刘玉平,唐棣.运用交互式电子白板提高学生课堂参与度[J].中国信息技术教育,2013(1):97-99.

[2]Han JY.Low-costmulti-touch sensing through frustrated total internal reflection[C]//Proceedings of the 18th annual ACM symposium on User interface softwareand technology.ACM,2005:115-118.

[3]彭超然,郑臻荣,李海峰,等.基于线阵CCD的大视场二维平面定位系统[J].浙江大学学报:工学版,2011(8):1475-1479.

[4]Jacucci G,Morrison A,Richard G T,et al.Worlds of information:designing for engagement at a public multi-touch display[C]// Proceedingsof the SIGCHIConferenceon Human Factors in Computing Systems.ACM,2010:2267-2276.

[5]李甫.粒子滤波算法研究及其电路设计[D].西安:西安电子科技大学,2010.

[6]周帆,江维,李树全,等.基于粒子滤波的移动物体定位和追踪算法[J].软件学报,2013(9):2196-2213.

[7]闫鹤.基于粒子滤波的目标跟踪研究[D].西安:西安电子科技大学,2010.

[8]吕林.海天背景下基于粒子滤波器的目标跟踪[D].武汉:武汉理工大学,2012.

责任编辑：丁吉海

A Study of the ElectronicWhiteboard Technique Based on Linear CCD

LUO Li1,CHEN Xiaoli2,JINGM engxi2
(1.School of Computer Science and Technology,Anhui University of Technology,Ma'anshan 243032,China；2.Shenzhen Haiya Technology Co.Ltd.,Shenzhen 518000,China)

The interactivewhite board(IWB)based on linear CCD technique showed greatdevelopmentpotential ow ing to its advantages of low cost,efficientmulti-touch.In order to solve the problem of pseudo touch points in CCD technique,the particle filter based on tracking algorithm is adopted.By comparing with the traditional extended kalman filter(EKF),the algorithm of particle filter has better performance than traditional EKF algorithm in tracking accuracy and can solve the problem of pseudo touch points.The result w ill be used to providea theoreticalbasisand technicalsupport for the design of IWB.

interactivewhiteboard;linear CCD;EKF;particle filter

O157.9,TP302

A

10.3969/j.issn.1671-7872.2014.02.017

1671-7872(2014)02-0183-05

2013-01-04

骆力(1960-)，女，广东龙川人，高级实验师，研究方向为计算机应用和数字图像处理。