改进的FastICA算法研究

张杰，刘辉，欧伦伟

湖南师范大学物理与信息科学学院，长沙 410081

改进的FastICA算法研究

张杰，刘辉，欧伦伟

湖南师范大学物理与信息科学学院，长沙 410081

独立分量分析是目前盲源分离算法中最常用的一种方法，其中快速独立分量分析（FastICA）以其收敛速度快而被广泛应用，但FastICA对初始值的选择比较敏感，而且在使用牛顿迭代法时，每迭代一步都需要计算一次函数值和一次导数值，当函数比较复杂时，计算它的导数值往往不方便，用单点弦截法进行迭代，将最速下降法与单点弦截法结合，在保证分离效果的同时使FastICA的迭代次数减少，同时使计算式更加简洁，而且减小了对初始值的敏感性，仿真实验验证了其有效性。

Fast独立分量分析（ICA）；牛顿法；弦截法；最速下降法；负熵

1 独立分量分析原理

独立分量分析（Independent Component Analysis，ICA）[1]是为解决盲信号分离而逐渐发展起来的，近些年成为信号处理和数据分析的有力工具。ICA的数学表述为：在不考虑噪声影响的情况下，假设观测信号（混合信号）为x(t)，源信号为s(t)，观测信号是由源信号线性瞬时混合得到，即

式中x(t)=[x1(t)，x2(t)，…，xm(t)]是m维的观测信号，s(t)= [s1(t)，s2(t)，…，sm(t)]是m维源信号，A是混合矩阵，ICA是由在源信号和混合系统均未知的情况下，仅根据得到的观测信号和对源信号的一些约束，通过源信号的统计特性[2-3]来估计出源信号。所得的估计信号包含了源信号最主要的信息。ICA的求解可以表述为：

式中G为全局传输矩阵，若通过学习使得G为单位矩阵，就可以得到y(t)=s(t)，从而得到源信号的估计信号。这里的y(t)就称为源信号的估计信号。

2 FastICA算法原理

FastICA也称为盲信号抽取固定点算法[2]，一般FastICA算法有基于四阶累积量、基于似然最大、基于负熵最大等形式，本文采用负熵[3]作为目标函数，负熵是一种可以度量随机变量非高斯性的函数，任一随机变量y的负熵定义为：

式中J表示负熵，H(y)表示随机变量y的熵，H(ygauss)为与y具有相同方差的高斯随机变量ygauss的熵，式（3）一般采用其近似方式，一种有用的近似是将高阶矩加以广义化[4]，同时通过化简可以得到：

上式为只使用一个非二次函数G的情况，v是零均值单位方差的高斯变量，所以EG(v)可以忽略不计，式（4）的最大化问题转化为求EG(y)的最优化问题，在约束条件E{(WTx)2}=||W||2=1下[5]，EG(y)的最优值可以通过下式得到：

用牛顿法[5]求解式（5），可以得到近似解：

通过化简可以得到：

上式即为基于牛顿法的迭代式。

3 FastICA改进算法

由式（6）可以知道牛顿法每迭代一次都要计算一次雅可比矩阵E{xg′(x)-β}，而计算雅克比矩阵需要求矩阵的导数，求导是计算式中最为复杂的部分，本文采用差商代替求导，即用弦截法迭代，弦截法迭代式为：

上式为双点弦截法迭代式，弦截法需要两个初始迭代点，双点弦截法两个初始迭代点在迭代中都变化，当有一个初始迭代点在迭代过程中固定不变时称为单点弦截法，单点弦截法迭代式为：

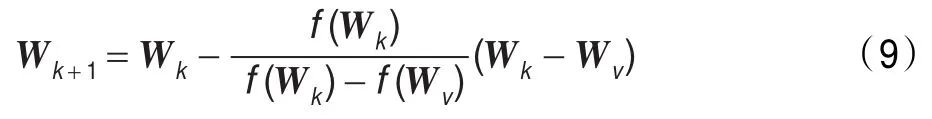
式中Wv为固定不变的起始迭代点，将式（5）代入上式并化简得：

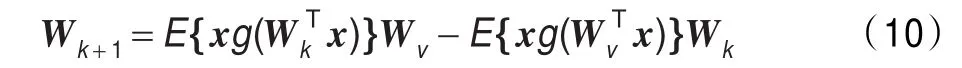
上式即为基于单点弦截法的迭代式，由于弦截法要求有两个起始迭代点，根据文献[6]的结论，最速下降法可以减小对初始值选择的敏感性，本文引入最速下降法[6-7]，用最速下降法求出一个起始迭代点，另外一个固定不变的起始迭代点Wv随机产生。

最速下降法计算步骤为：

（1）选一初始化随机正交阵W=[W1，W2，…，Wn]，同时令k=0，选取收敛判定值为critical=0.000 001。

（2）计算E{xg(WTx)}在W处的梯度值：

由于负梯度方向就是函数值下降最快方向，所以可将梯度值作为松弛因子代入下式：

（3）当abs(wk+1-wk)&abs(wk+1+wk)≤critical时，收敛则W0=Wk+1，不收敛则k+1且Wk=Wk+1后返回式（11）继续迭代。

改进算法的实现步骤：

（1）对混合信号x进行去均值和白化预处理。

（2）初始化权矢量W，通过最速下降法求出W0，起始迭代次数k=0，选取收敛判定值为critical=0.000 001。

（3）任意选取另外一个迭代点Wv，而Wv选取后不再改变，将Wv和W0代入式（10）求得Wk+1，用Wk+1= Wk+1/||Wk+1||去相关和归一化[7]。

（4）判断abs(wk+1-wk)&abs(wk+1+wk)≤critical是否成立，不成立则k+1后返回式（10）继续迭代，成立则估计出一个分离矩阵分量。

（5）当得到整个分离矩阵后，由分离矩阵与观测信号相乘得到源信号的估计信号，然后输出源信号的估计信号。

4 仿真实验

实验采用Matlab进行仿真，对4个源信号的混合信号进行分离，源信号中的4个信号均为录制的语音信号，采样频率均为8 kHz。混合矩阵A为由Matlab随机产生的4阶矩阵，本文为了方便对分离效果进行分析，对每次实验的混合矩阵采用同一个随机混合矩阵，由Matlab随机产生的混合矩阵A的值为：

源信号（图1）经过混合矩阵混合后得到的混合信号如图2，对混合信号采用牛顿迭代法及改进算法进行分离得到的信号如图3和图4。由Matlab仿真得到的信号图形如图1～图4所示。从分离后的图像可以看出，牛顿法和改进算法均能分离4个混合信号，下面将定量分析两种算法的性能。

图1 源信号

图2 混合信号

图3 牛顿法分离得到的信号

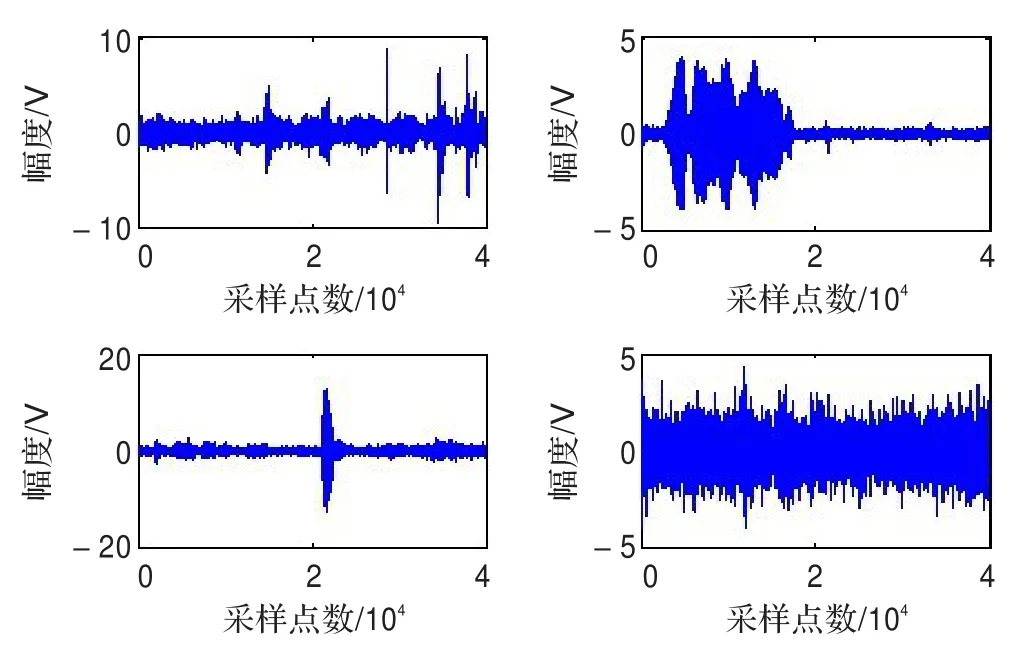
图4 改进算法分离得到的信号

5 算法的性能分析

独立分量分析的评价指标有多种，本文将用信噪比[8-9]和迭代次数来说明牛顿法和改进算法对混合信号分离效果的比较。

5.1 信噪比

信噪比，即SNR，是指一个电子设备或者电子系统中信号与噪声的比例。信噪比越大，说明混在信号里的噪声越小，语音信号的音质量越高。

信噪比判定式为：

表1 不同算法信噪比的比较

表1为两种算法分离所得信号的信噪比值以及它们的平均值，从表中可以看出，改进算法分离所得信号的信噪比值比牛顿法分离所得信号的信噪比值稍大，改进算法能够保证牛顿法的分离效果。

5.2 迭代次数

通过对牛顿法和改进算法取相同的初始值，然后看各需要进行多少步迭代才能收敛，由于每次得到的数值有偏差，可以取10次数值然后取平均值，由实验得到的数据如表2所示。

表2 不同算法迭代次数比较

表2中10组数据取平均值得23.6和15.3，所以改进的迭代算法对比原牛顿法在迭代次数上有所改进，使其只进行更少的迭代即可收敛。

6 结论

牛顿迭代法对初始值要求比较高，且每步迭代都要计算雅可比矩阵，本文通过采用改进牛顿法即弦截法进行迭代，同时结合最速下降法求迭代初始值，在保证牛顿法分离效果的同时，在计算复杂度和迭代次数上都有所改进。

[1]Comon P.Indepent Component Analysis，a new concept?[J]. Signal Processing，1994，36：287-314.

[2]Hyvarinen A.A family of fixed-point algorithms for Independent Component Analysis[C]//IEEE Conf on Acoustics，Speech and Signal Processing，1997：3917-3920.

[3]马建仓，牛奕龙，陈海洋.盲信号处理[M].北京：国防工业出版社，2006.

[4]杨福生，洪波.独立分量分析的原理与应用[M].北京：清华大学出版社，2006.

[5]毕杨.基于快速独立分量分析的盲源分离算法研究及应用[D].西安：西安理工大学，2007.

[6]季策，胡祥楠，朱丽春，等.改进的高阶收敛FastICA算法[J].东北大学学报，2011（10）：10-13.

[7]Hyvarinen A，Karhunen J，Oja E.Independent component analysis[M].New York：John Wiley Press，2001：79-86.

[8]徐明彪，朱维彰.关于信号盲分离效果评判指标的分析[J].杭州电子工业学院学报，2002，22（3）：63-66.

[9]Ye J M，Zhu X L，Zhang X D.Adaptive blind separation with an unknown number of sources[J].Neural Computation，2004，16（8）：1641-1660.

ZHANG Jie,LIU Hui,OU Lunwei

Institute of Physics and Information Science,Hunan Normal University,Changsha 410081,China

Independent Component Analysis（ICA）is the blind source separation algorithm which is one of the most commonly used methods.And the Fast Independent Component Analysis（FastICA）with its convergence speed is widely used. But FastICA is sensitive to the choice of initial value,and in the use of Newton iterative method,each iteration step is needed to calculate a function value and a derivative value.When the function is more complex,computing its derivatives is often not convenient.This paper uses the single point string section method to iterate.Combining the steepest descent method with the single point string section method,while ensuring the separation effect,it makes FastICA iterative times reduce.At the same time it makes the calculation type more concise,and reduces the sensitivity to the initial value.

Fast Independent Component Analysis（ICA）;Newton method;string section method;the steepest descent method;negative entropy

A

TN911.7

10.3778/j.issn.1002-8331.1205-0037

ZHANG Jie,LIU Hui,OU Lunwei.Research on improved FastICA algorithms.Computer Engineering and Applications,2014,50（6）：210-212.

湖南省科技厅项目（No.2012GK3121）。

张杰（1986—），男，硕士研究生，研究方向：信号处理；刘辉（1964—），女，副教授，硕士生导师；欧伦伟（1985—），男，硕士研究生，研究方向：数字信号处理。E-mail：liuhui1366@126.com

2012-05-14

2012-09-24

1002-8331（2014）06-0210-03

CNKI网络优先出版：2012-09-28，http://www.cnki.net/kcms/detail/11.2127.TP.20120928.1345.012.html