高分辨率遥感图像分割的最优尺度选择

刘兆祎，李鑫慧，沈润平，朱枫，张凯，王恬，王媛媛

1.南京信息工程大学大气物理学院，南京 210044

2.南京信息工程大学遥感学院，南京 210044

3.北京师范大学全球变化与地球系统科学研究院，北京 100875

4.中国人民解放军94940部队

5.兰州大学大气科学学院，兰州 730000

6.中国科学院大气物理研究所，北京 100029

高分辨率遥感图像分割的最优尺度选择

刘兆祎1，李鑫慧2，沈润平2，朱枫3，张凯4，王恬5，王媛媛6

1.南京信息工程大学大气物理学院，南京 210044

2.南京信息工程大学遥感学院，南京 210044

3.北京师范大学全球变化与地球系统科学研究院，北京 100875

4.中国人民解放军94940部队

5.兰州大学大气科学学院，兰州 730000

6.中国科学院大气物理研究所，北京 100029

面向对象的最优尺度选择是高分辨率遥感图像多尺度分割技术中的关键问题。最优分割尺度的确定直接影响到后续的图像信息提取与分析。在模型计算法的基础上，改进并实现了一种全局最优尺度计算模型。该最优尺度计算模型可以根据多波段信息自动选择最优尺度，从而避免了人目视的主观性。

面向对象；最优尺度选择；模型计算

1 引言

图像分割是图像处理与计算机视觉的基本问题之一，是图像处理与分析的关键步骤，它对提取目标特征、进行目标测量和分类及其后的高层处理都非常重要[1]。对于遥感图像而言，图像分割是决定遥感图像分析与计算成功与否的关键因素之一，尤其是随着高分辨率卫星数据如IKONOS，QUIKBIRD等的大量获取，图像分割被越来越多地用于面向对象方法的图像对象的获取中，图像分割的质量直接决定着后续的面向对象处理的精度[2]。因此在多尺度的高分辨率遥感影像分割中如何确定分割的最优尺度显得尤为重要。

关于多尺度分割算法研究很多，其中Fractal Net Evolution Approach被认为是一种有效利用光谱信息和空间信息的处理方法[3]，是商业软件eCognition多尺度分割的核心算法。利用该方法进行多尺度分割，需要预先设置分割参数，包括各波段权重、均值因子（包括光谱因子和形状因子）和分割尺度，其中分割尺度是形成影像对象的重要参数，但是该方法不能确定对象表达在哪一个尺度上是合理的，即无法确定最优尺度。因此有必要对多尺度分割的最优尺度选择进行研究。

目前国内外面向对象的最优尺度选择方法，主要有以下三类[4]：（1）凭借经验选择分割尺度，经反复验证确定最优分割尺度。这种方法简单直观，可操作性强，但带有一定的主观性，不易获得最优分割尺度。（2）选取尺度鉴别指标评价分割尺度选择质量。尺度鉴别指标的构造通常会强调某个因素的作用，如面积或颜色，指标选择不确定性较大，难以取得理想效果。（3）利用最优分割尺度计算模型计算最优分割尺度。该方法从对象内的同质性和对象间的异质性来判断分割的优劣，是一种全局最优判断的方法。

本文在分析原有模型计算法优劣的基础上，改进了基于多波段的模型计算法，达到了自动选择最优尺度的目的。

2 最优尺度选择

2.1 模型计算法

在遥感影像分类或信息提取中，对于整幅影像的理想分割结果是分割所得到的对象具有良好的内部同质性以及分割得到的对象与相邻对象之间具有良好的异质性。何敏等人基于这一原则，提出了一种面向对象的全局最优尺度计算模型[5]。这种方法的思想是：利用对象内部的标准差来表示对象内部的同质性，用空间相关性来表示对象之间的异质性，使得内部同质性和对象之间的异质性达到最好的综合效果。该模型自动计算得到最优尺度，方便快捷、可信度高，避免了人工目视的主观性。

该方法的不足之处是：首先它对分割结果质量的评价只考虑了单波段的信息，而没有充分利用遥感影像多波段的特点，分割结果的评价没有与分割过程建立联系。其次，这种方法是一种获得全局最优尺度的方法，但不同信息提取目标拥有不同的最优尺度，该方法没有考虑具体的信息提取目标。此外这种最优尺度的选择仍然只考虑了影像对象的光谱信息，而没有考虑影像对象的空间特征。

2.2 改进的基于多波段的模型计算法

遥感影像不同于自然图像的一个特点在于遥感影像具有多波段成像的特点。在遥感影像的信息提取中，应综合考虑、充分利用遥感影像在各波段的特征，以提高信息提取的精度。遥感影像分割的理想结果是分割所得到的对象具有良好的内部同质性，同时相邻对象之间具有良好的异质性，并且分割后的对象内同质性和对象间异质性在各个波段上都能够得到体现。基于这个思想，本文针对何敏等提出的模型计算法只考虑单个波段的不足，提出了改进的基于多波段的模型计算法选择影像分割的最优尺度，以便得到最佳的分割结果。

由于多波段影像的分割前可以设置不同的波段权重，权重大的表示分割过程中应更多地考虑该波段的信息。因此，在衡量分割结果同质性、异质性的时候，应该将分割过程中采用较大权重的波段同样赋予较大的权值，以体现分割过程和分割评价的标准一致性，从而将分割结果质量的评估与分割过程建立联系。

综合考虑多波段信息和波段权重后，本文提出的改进的基于多波段的计算模型具体计算过程如下：

设预分割的图像具有N个波段，在执行多尺度分割时各波段被赋予的权重是ti(i=1，2，…，N)，对象内部在各个波段上的同质性用公式（1）计算，对象间在各个波段上的异质性用Moran指数来表示[6]，计算公式见公式（3）。

式中Vb(b=1，2，…，N)表示在波段b上的对象同质性，Vi是对象i在波段b上的标准差，ai是对象i的面积，n为整个区域对象的总个数（分割后的对象总数）。加入面积因子可以使得面积大的对象具有更高的权重，避免了小对象引起的不稳定性。对象内部总的同质性指数是各波段上的同质性的加权和，权重与执行分割时所设的权重相同，见公式（2）：

上式中，N是波段数目，tb(b=1，2，…，N)表示波段b的权重，Vb是波段b的同质性指数。V越低，表示影像对象内部异质性越小，即对象内部具有良好的同质性。

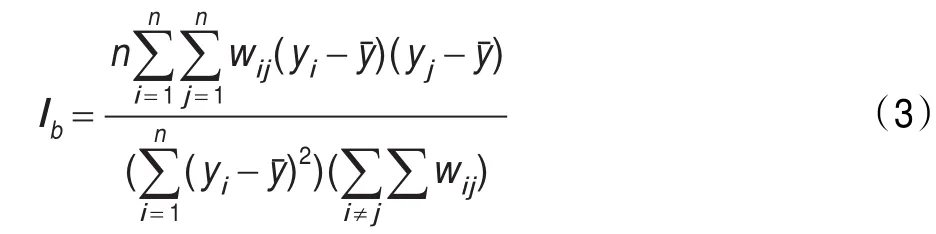
上式中，Ib(b=1，2，…，N)表示在波段b上的对象异质性，n为对象的总数；wij表示对象Ri和对象Rj的邻接关系，如果对象Ri和对象Rj邻接，则wij=1，否则wij= 0；yi为对象Ri在波段b上的光谱平均值；yˉ为在波段b上整个影像的光谱平均值。同理，对象间总的异质性指数是各波段异质性的加权和，见公式（4）：

上式中，N是波段数目，tb(b=1，2，…，N)表示波段b的权重，Ib是波段b的异质性指数。I越低，影像对象之间相关性越低，即影像对象之间的可分性越好。

由同质性指数和异质性指数构建衡量分割质量的质量函数[7-8]：

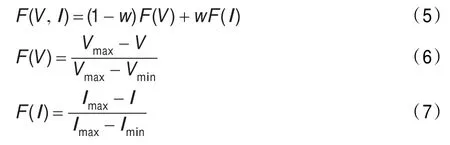
其中，V为对象内部的各波段上标准差的加权和（代表对象内部同质性），I为各波段上Moran指数的加权和（代表对象间的异质性），w为Moran指数I在目标函数值中所占的权重，范围为[0，1]。

在此基础上通过插值函数的方法可以得到一个最优分割尺度的计算模型[6]。

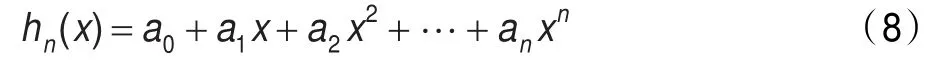
公式（5）在影像初分割阶段用来计算对应分割尺度的质量值，用于插值函数的插值点，为最优尺度计算模型公式（8）服务。

3 实验结果及分析

3.1 数据

本实验数据采用南京地区IKONOS影像。IKONOS卫星是全球第一颗高分辨率商业遥感卫星，可提供1 m分辨率的全色影像和4 m分辨率的多光谱影像（包括可见光红、绿、蓝和近红外波段）。因为影像范围较大，实验时利用ENVI4.2裁切300像素×300像素作为研究区，该区域位于南京市区内。实验前采用主成分分析法（PCA）将多光谱波段与全色波段进行融合，融合后的多光谱数据获得了全色波段的空间结构特征，分辨率也是1 m（图1）。

3.2 多尺度分割实验

分割实验在eCognition环境下进行。采用该软件中的multi-resolution算法对处理后的IKONOS影像进行多尺度分割。分割时设置的分割参数包括各波段权重、均值因子（包括光谱因子和形状因子，而形状因子又包括紧密度和光滑度两个因子）和分割尺度[5]。

因为多光谱波段在融合过程中需要重采样，必然会造成信息失真，为保证分割的可靠性，分割过程中应该较多地考虑全色波段。从融合后的效果看，融合后的近红外波段具有明显的网格状失真现象，分割中应赋予较小的权重。分割时的波段权重按全色、近红外、红绿蓝顺序对应设置为10，1，5，5，5，这也是利用模型计算最优尺度用到的权重。实验中将光谱因子和形状因子分别设为0.9和0.1；紧密度因子和光滑度因子一般分别设为0.3和0.7[5]。实验所要研究的对象是分割尺度，因此在实验过程中，这些因子的值始终保持不变。

确定好这些参数以后，以步长5递增进行影像分割。通过与图1（a）的标准假彩色合成影像作目视对比可以看出，当尺度为小于30时（如图1（b）），分割结果相当“破碎”，即分割出来的对象过多，相邻对象间的光谱异质性降低，类别可分性降低。当尺度大于100时（如图1（c）），分割结果“淹没”现象严重，产生较多合并对象，如图中房屋、道路和植被被分割到一个对象中去，没能对地物进行有效分割，这同样不利于提高后续信息提取的精度[9]。将各分割结果与分割前影像进行目视对比发现最优分割尺度在55左右（如图1（d））各个地物都较好地被提取出来。从全图来看，分割结果在“破碎”和“淹没”间比较平衡，比较能全面反应地物目标的差别。

3.3 模型计算和分析

根据上一步骤实验分割结果图，可以通过改进后模型计算法求得理论上的最优尺度。为了避免过分割和分割太粗造成计算结果的不稳定，实验计算不采用过大或过小的尺度的分割结果，只导入以尺度40～90分割结果。

通过程序追踪同质性指数和异质性指数和实验分割尺度的关系。对象内同质性指数用面积加权的标准差来指示（见公式（1）），对象间异质性指数用Moran指数（见公式（3））来表示。随着分割尺度的增加，分割对象的面积增大，对象数目减少（如图2所示）；因为包含像元的增多，在各个波段上对象内部同质性指数随尺度增大而增大（如图3），对象间异质性指数随尺度增大总体呈下降趋势（如图4所示）。可见体现分割质量好坏的异质性指数和同质性指数是一对矛盾的因子。

图1 不同分割尺度下的分割效果实验

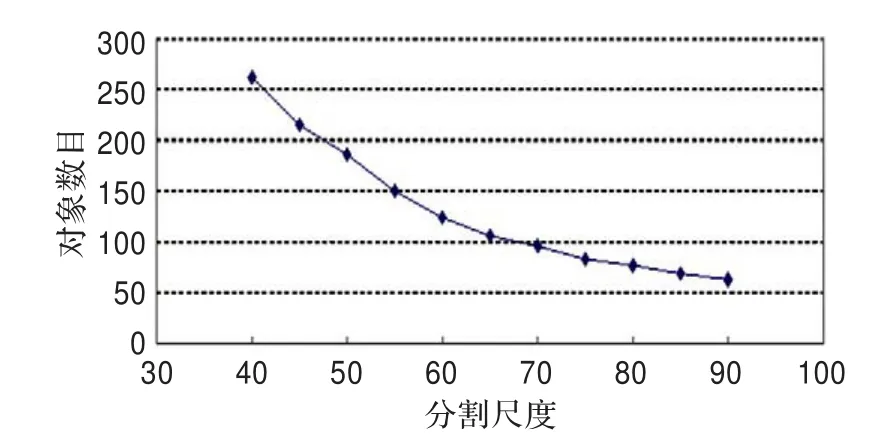
图2 对象数目与尺度关系

图3 同质性与尺度关系

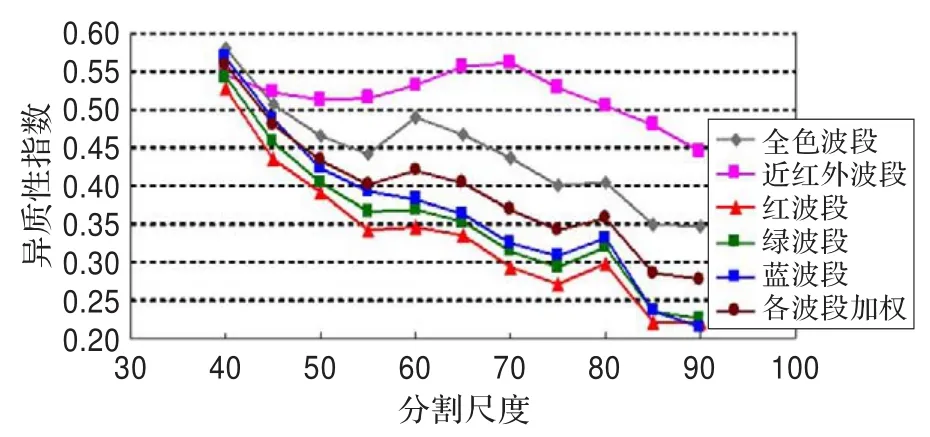
图4 异质性和尺度关系

分割质量值实际是同质性指数和异质性指数归一化后的加权和（见公式（5））。为了使得计算的分割质量值能够客观正确地反映真实分割质量，必须在异质性指数和同质性指数之间取得矛盾的平衡。首先取w=0.5为权重进行实验，通过对程序调试运行追踪，可得到各实验分割结果的分割质量，如图5所示。考虑到分割质量随分割尺度变化（见公式（8））的连续性，可以看出，在尺度45和55之间有个峰值对应最优分割尺度，尺度55以后分割质量下降。最终计算的最优尺度值为53，这与目视结果相当。模型计算的最优尺度的分割结果如图1（e）所示。

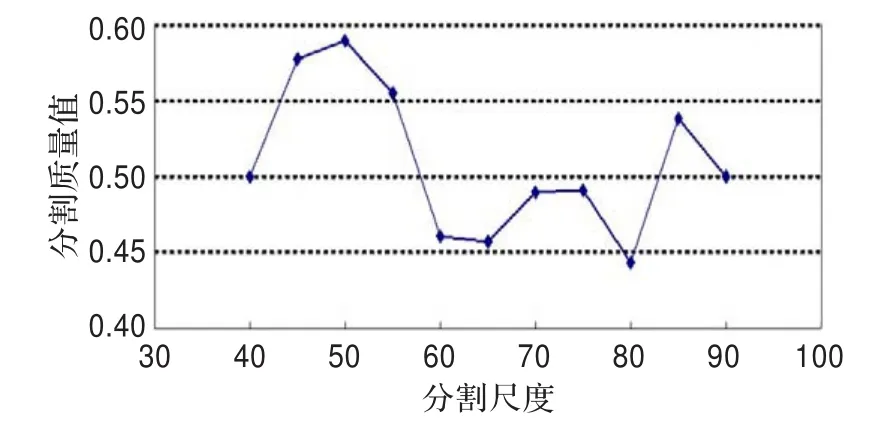
图5 分割质量与尺度关系

再对w分别取0.3，0.7进行分割实验，最终计算的最优尺度分别为45和81。

一个好的分割结果要求对象内部要有较高的同质性，即应保证对象自身的纯度，同时各对象之间要有较高的异质性，即应保证不同对象之间有差异，可分性好[10]。实验表明，对象的同质性指数是分割尺度的增函数，而异质性指数则随分割尺度的增加呈下降趋势，随着分割尺度的增加，对象个数随之减少，对象内的同质性相应减小，而对象间异质性则相应增大。在利用模型自动计算最优分割尺度时，当强调对象内同质性时，应适当减小异质同质权重w，此时计算结果会偏向小尺度；反之当要强调对象间异质性时则要适当增加权重w，此时的计算结果会偏向大尺度。实验表明基于该模型得到的最优尺度的选择结果是对象内均质性和对象间异质性矛盾因子的平衡。

4 结束语

本文提出的改进的基于多波段的模型计算法根据对象内同质性要大和对象间异质性要高的原则自动选择最优的分割尺度，具有较好的理论基础。实验表明，通过调节同质性指数和异质性指数的权重因子，可以获得一系列最优尺度值。在一权重因子下，全局最优尺度的选择结果是对象内均质性和对象间异质性矛盾因子的平衡。但是这种最优尺度的选择只考虑了影像对象的光谱信息，而没有考虑影像对象的空间特征，这将是后续的研究内容。

[1]章毓晋.图像分割评价技术分类和比较[J].中国图象图形学报，1996，1（2）：151-158.

[2]郭建聪，李培军，肖晓柏.一种高分辨率多光谱图像的多尺度分割方法[J].北京大学学报：自然科学版，网络版（预印本），2008（3）：123-125.

[3]Hay J G，Blaschke T，Marceau J D，et al.A comparison of three image-object methods for the multiscale analysis of landscape structure[J].Isprs Journal of Photogrammetry and Remote Sensing，2003，57（5/6）：327-345.

[4]于欢，张树清，孔博，等.面向对象遥感影像分类的最优分割尺度选择研究[J].中国图象图形学报，2010（2）：352-360.

[5]何敏，张文君，王卫红.面向对象的最优分割尺度计算模型[J].大地测量与地球动力学，2009，29（1）：106-109.

[6]胡文亮，赵萍，董张玉.一种改进的遥感影像面向对象最优分割尺度计算模型[J].地理与地理信息科学，2010，26（6）：15-18.

[7]陈建裕，潘德炉，毛志华.高分辨率海岸带遥感影像中简单地物的最优分割问题[J].中国科学D辑：地球科学，2006，36（11）：1044-1051.

[8]薄树奎，韩新超，丁琳.面向对象影像分类中分割参数的选择[J].武汉大学学报：信息科学版，2009，34（5）：514-517.

[9]张俊，汪云甲，李妍，等.一种面向对象的高分辨率影像最优分割尺度选择算法[J].科技导报，2009（21）：91-94.

[10]黄慧萍.面向对象影像分析中的尺度问题研究[D].北京：中国科学院研究生院（遥感应用研究所），2003.

LIU Zhaoyi1,LI Xinhui2,SHEN Runping2,ZHU Feng3,ZHANG Kai4,WANG Tian5,WANG Yuanyuan6

1.School of Atmospheric Physics,Nanjing University of Information Science and Technology,Nanjing 210044,China
2.School of Remote Sensing,Nanjing University of Information Science and Technology,Nanjing 210044,China
3.College of Global Change and Earth System Sciences,Beijing Normal University,Beijing 100875,China
4.Unit 94940 of PLA,China
5.School of Atmospheric Sciences,Lanzhou University,Lanzhou 730000,China
6.Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China

The problem of best segmentation scale is a key point in multi-scale segmentation of high-resolution image segmentation.The confirmation of the best segmentation has a direct effect on the extraction and analysis of the information gathered from the image.This paper puts forward a best segmentation scale model in overall situation on the basis of model calculation.This model can calculate the best segmentation scale on the consideration of multi-band information, therefore,avoiding the potential subjectivity of human visual.

object-oriented;best segmentation scale;model calculation

A

TP751.1

10.3778/j.issn.1002-8331.1206-0094

LIU Zhaoyi,LI Xinhui,SHEN Runping,et al.Selection of the best segmentation scale in high-resolution image segmentation.Computer Engineering and Applications,2014,50（6）：144-147.

江苏省大学生实践创新训练计划项目（No.10CX044）。

刘兆祎（1989—），男，硕士研究生，主要研究方向为卫星资料同化；李鑫慧（1978—），女，博士研究生，讲师，主要研究方向为遥感图像处理；沈润平（1963—），男，教授，博士生导师，主要研究方向为土地利用遥感与监测、图像处理等；朱枫（1988—），男，硕士研究生，主要研究方向为土地利用与气候变化；张凯（1989—），男，主要研究方向为图像处理；王恬（1988—），女，硕士研究生，主要研究方向为遥感与资料同化；王媛媛（1989—），女，硕士研究生，主要研究方向为陆面过程。E-mail：ryutyoui@yeah.net

2012-06-06

2012-10-29

1002-8331（2014）06-0144-04

CNKI网络优先出版：2012-11-12，http://www.cnki.net/kcms/detail/11.2127.TP.20121112.1436.006.html