灰色聚类分析在延边东部地区矿产预测中的应用

马艳英，马 超，刘艳丽

(1.吉林大学综合信息矿产预测研究所，吉林长春130026;2.吉林工程技术师范学院应用理学院，吉林 长春130052;3.中国石油集团东北炼化工程有限公司吉林设计院采购部，吉林吉林132002;4.吉林市吉化第一高级中学校物理组，吉林 吉林132002)

成矿预测的主要工作就是确定在什么地方找什么样地矿?找矿规模如何?哪些地方先找，哪些地方后找?即为将预测出的找矿靶区划分为首先安排工作的A类靶区和稍后安排工作的B类靶区及最后安排工作的C类靶区。本文利用灰色聚类分析方法，弥补了数理统计中的聚类分析方法在解决实际问题时只根据随机抽样的观测数据进行数字分类而忽视了客观实际之不足，为进一步部署工作提供有力帮助。

1 灰色聚类分析方法概述

灰色聚类分析方法是属于智能型的评估方法，即是包含人的经验在内的评估方法，它要求在对客观事物进行评估之前，先给出评定的准则。灰色聚类分析是通过计算找出每一个因子(样品或找矿靶区单元)的综合效果，明确某一因子属于各个灰类(A、B、C类找矿靶区)的权，从而构成综合效果权向量，以便对因子进行灰类归属。

设评估指标序号为 i，i=1，2，…，m;

评判类别序号为 j，j=1，2…，p;

因子标号为 k，k=1，2…，n，则 dki表示第 k 个评估因子在第i个指标下的样本，考虑所有评估因子对所有指标的样本，可构成样本矩阵d

给出各个指标属于某一灰类的白化权函数(如成矿有利度这个灰数在某个区间内越大，首先安排地质找矿工作的可能性就越大。其中，指标i属于第1类白化权函数fi1;指标i属于第2类(中间类，如果只有三类)的白化权函数fi2;指标i属于最末类的白化权函数fi3。

由此得出的白化权函数式为

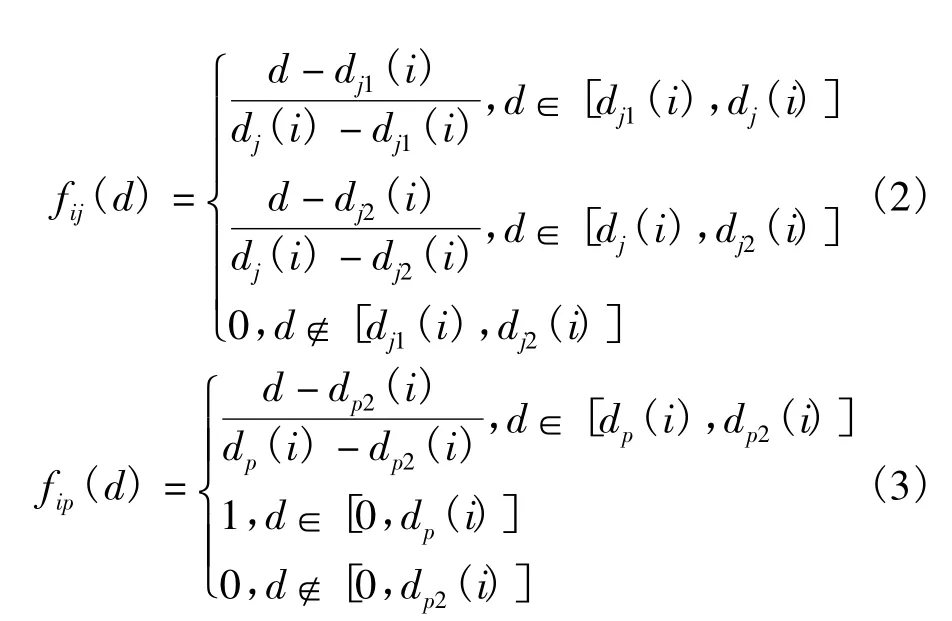
确定第k个评估因子属于第j个灰类的权为

从σk中找出最大权，最大权所属的类别即因子xk所属的灰类。

2 应用实例及计算结果

2.1 建立原始数据矩阵d

我们规定由特征分析、灰色关联分析定位预测模型计算得到的各单元成矿有利度及专家打分为各单元赋的权值作为评估指标(i=1，2，3)，评判类别(灰类)为A类、B类和C类预测靶区j=1，2，3;评估因子为31个单元(k=1，2…，31)，即构成31×3的原始数据矩阵见表1。

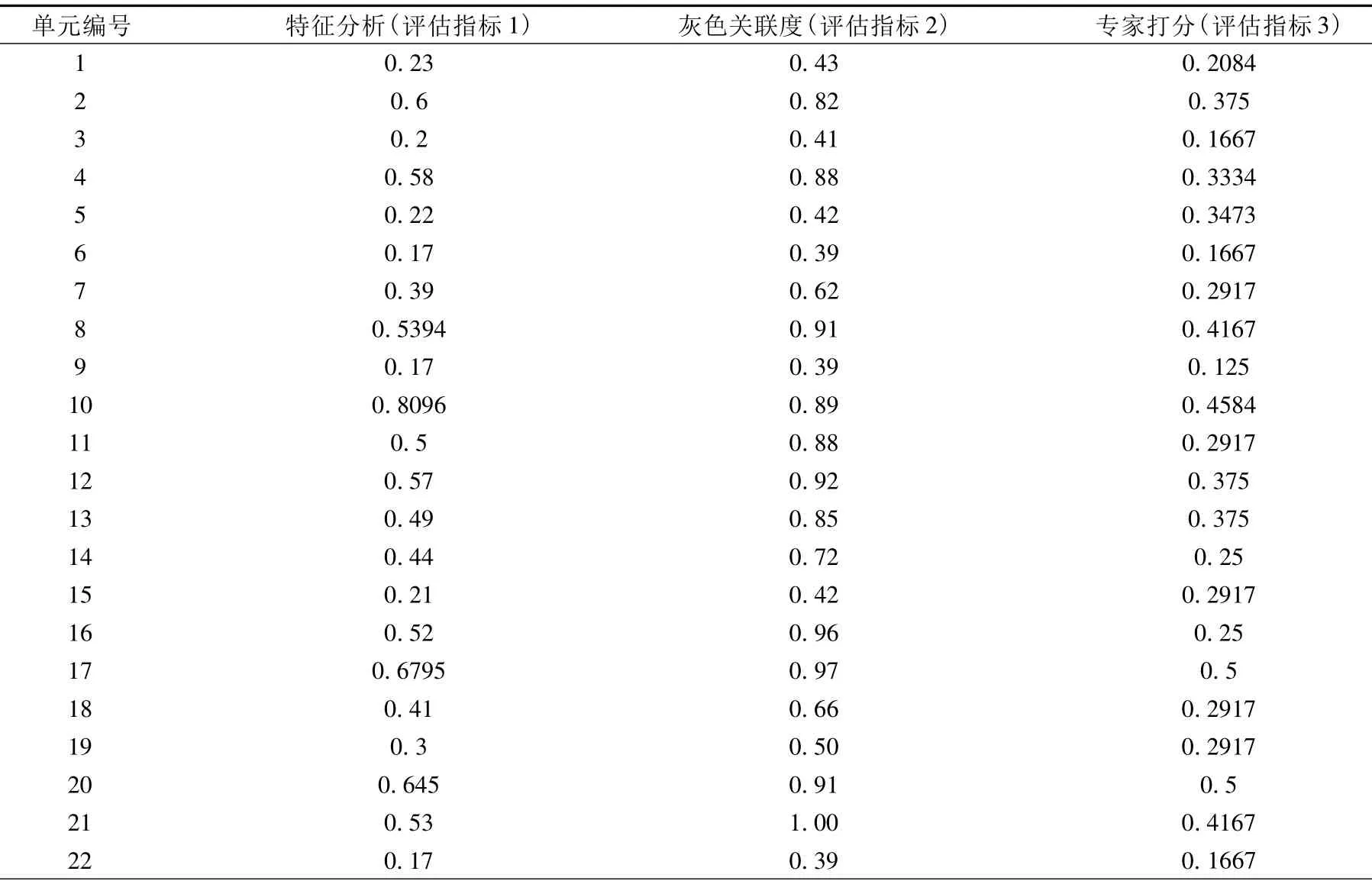
表1 原始数据表(31×3)

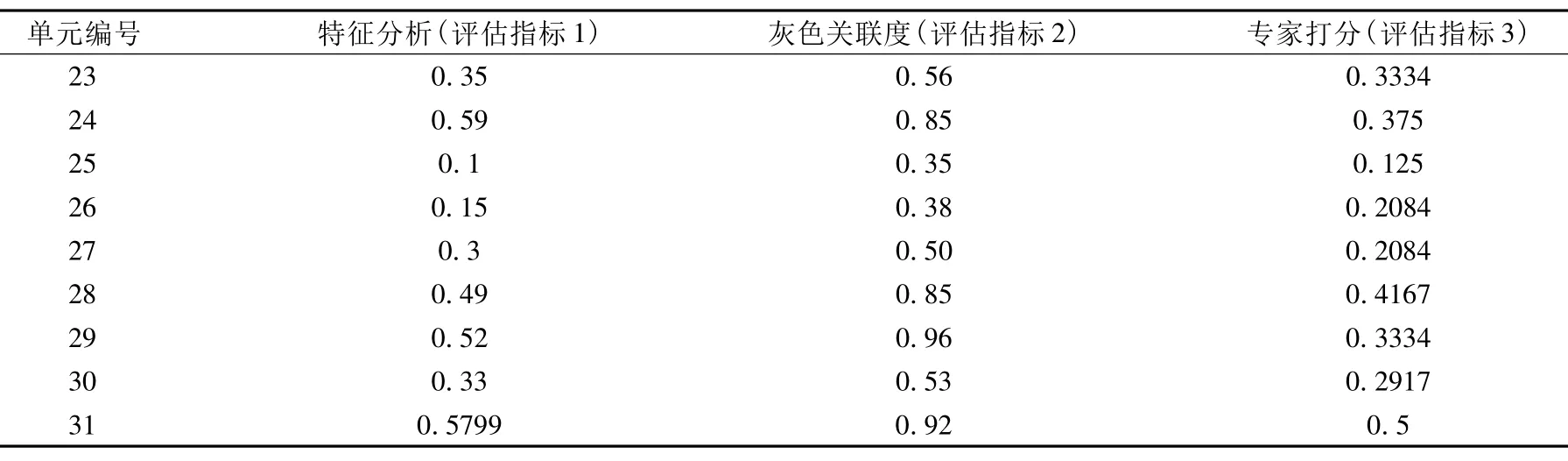
续表1 原始数据表(31×3)

2.2 给出各个指标属于某一灰类的白化权函数

对于指标1

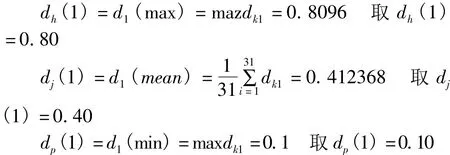
为此有

对于指标2

为此有

对于指标3

为此有

2.3 求标定聚类权

由(4)式分别计算出各评价指标属于某一灰类的聚类权。

对于指标1，有

η11=dh(1)/［dh(1)+dh(2)+dh(3)］=0.3479

η21=dh(2)/［dh(1)+dh(2)+dh(3)］=0.4347

η31=dh(3)/［dh(1)+dh(2)+dh(3)］=0.2173

对于指标2，有

η12=dj(1)/［dj(1)+dj(2)+dj(3)］=0.3076

η22=dj(2)/［dj(1)+dj(2)+dj(3)］=0.4615

η32=dj(3)/［dj(1)+dj(2)+dj(3)］=0.2307

对于指标3，有

η13=dp(1)/［dp(1)+dp(2)+dp(3)］=0.1538

η23=dp(2)/［dp(1)+dp(2)+dp(3)］=0.8520

η33=dp(3)/［dp(1)+dp(2)+dp(3)］=0.2307

2.4 计算聚类系数

对于 k=1，j=1，

σ11=f11(d11)η11+f21(d12)η21+f31(d13)η31=0.3774

对于 k=1，j=2，

σ12=f12(d11)η12+f22(d12)η22+f32(d13)η32=0.6677

对于 k=1，j=3，

σ13=f13(d11)η13+f23(d13)η23+f33(d13)η33=0.5346

因子1对于三个灰类的灰色聚类向量σ1为

σ1=(σ11，σ12，σ13)=(0.3774，0.6677，0.5346)

由于在σ1中σ13=0.6677最大，第一个单元属于第三类即B类靶区。

依次可得到 σ2，σ3，…，σ31，见表 2。

表2 灰色聚类系数值表

2.5 评价结果

从表2 可以看出 4、11、12、13、16、21、24、29 号单元的综合效果最好，属A类靶区，最有可能找到具一定规模的工业矿床，属首批重点安排地质找矿工作的靶区;1、2、7、8、14、18、19、23、28、30 号单元的综合效果次之，判为 B 类靶区;而剩下的 3、5、6、9、15、22、25、26、27号单元为C类靶区，综合效果较差，应该最后考虑安排工作。由于8、10、17、20、31为已知单元，再用灰色聚类分析计算时，除了8号单元为B类靶区外，其余的均为A类靶区，这说明用灰色聚类分析进行延边东部地区地质找矿与实际调查结果基本一致，说明该方法是可行的。

地质，1995，(1).

［1］燕长海.应用灰色聚类分析部署地质找矿工作［J］.河南

［2］李 林，桑树勋，黄华州等.灰色聚类分析在煤炭资源有效保障能力评价中的应用［J］.煤田地质与勘探，2009，(1).

［3］刘 刚.灰色聚类分析在圈闭评价中的应用［J］.天然气地球科学，2001，(6).

［4］于远祥，杨 勇，叶万军等.灰色聚类分析在地质灾害综合区划中的应用［J］.煤田地质与勘探，2009，(3).

［5］肖克炎，王勇毅，陈郑辉等，矿产资源评价新技术与评价新模型［M］.北京:地质出版社，2004.

［6］毛新虎，刘占魁，李秀青.灰色聚类法在矿山地质灾害危险性分区评价中的应用［J］.西南民族大学学报，2008，(3).

［7］张海燕，王新民，尹慧等.地质灾害风险评价阈回归联合聚类分析［J］.吉林大学学报(地球科学版)，2011，(2).