多径传播环境下的无源UHF RFID系统电波传播模型

唐志军，吴笑峰，詹杰，胡仕刚，席在芳

1.湖南科技大学信息与电气工程学院，湖南湘潭 411201

2.湖南科技大学物理与电子科学学院，湖南湘潭 411201

多径传播环境下的无源UHF RFID系统电波传播模型

唐志军1，吴笑峰1，詹杰2，胡仕刚1，席在芳1

1.湖南科技大学信息与电气工程学院，湖南湘潭 411201

2.湖南科技大学物理与电子科学学院，湖南湘潭 411201

针对自由空间模型在预测射频识别系统识别距离时存在的偏差，综合考虑射频识别系统应用的多径传播环境，建立一种无源超高频射频识别系统电波传播模型，并重点分析了前向链路路径损耗的主要影响因素及其计算方法。基于该电波传播模型，探索性地提出实际环境下的无源超高频射频识别应用模拟思路。仿真和测量结果表明，该模型在预测无源超高频射频识别系统识别距离时更为准确。

射频识别；传播模型；多径环境；路径损耗；识别距离

1 引言

射频识别（RFID）起源于20世纪40年代雷达技术的发展，是一种非接触式的自动识别技术，它通过射频信号自动识别目标对象并获取相关数据，识别过程无须人工干预。近年来，由于标签成本的大幅度降低，RFID应用显著增加[1-2]。通常，RFID系统可以分为有源和无源两种，由于成本的关系，无源RFID系统更广泛地应用于现实生活当中。无源RFID系统是基于负载调制或反向散射调制（Backscattering）原理来工作的。目前，UHF频段的无源RFID系统因其标签成本低、识别距离远，而具有巨大的市场和应用潜力，其标签和阅读器之间的通信是通过反向散射调制（改变反射系数）来实现的。识别距离是RFID应用需要重点考虑的性能指标之一，它直接关系到RFID标签识别的可靠性，而这主要取决于对路径损耗分析、链路预算和实际环境对系统的影响等因素。

现有RFID信道模型大部分是基于弗里斯（Friis）公式的自由空间模型[3-8]，然而，这些模型仅适用于视距（LOS）、远场、无环境影响的理想条件下，借助该模型预测系统识别距离时偏差较大。由于识别距离受许多复杂因素的制约，如阅读器性能、标签性能、产品包装、材料、地面、墙面、周围环境等因素。在影响RFID系统有效识别范围预测众多因素中，多径传播为决定性因素。尽管多径传播在移动通信中得到广泛研究，但由于RFID系统与移动通信系统在应用环境、识别距离和信号强度等方面存在显著的差异，所以这些研究结果并不能直接应用到RFID系统中。基于此，本文通过分析路径损耗和多径传播环境的影响因素，给出实际环境下的RFID系统电波传播模型，以提高系统识别距离预测的准确性。

2 电波传播模型

识别范围是无源UHF RFID系统最重要的特征参数之一，它主要受限于标签刚好能够从阅读器获取足够的开启功率的最大距离Rtag和阅读器能够检测到标签反向散射信号的最大距离Rreader，系统的有效识别距离取这两个距离的较小者[2]。而要准确计算或预测系统识别距离，则需要建立符合实际应用环境的电波传播模型。

2.1 自由空间模型

对于自由空间传播环境，阅读器到标签的无线链路中（前向链路），标签天线的接收功率Pr_tag可以用Friis自由空间方程来计算[2，9]：

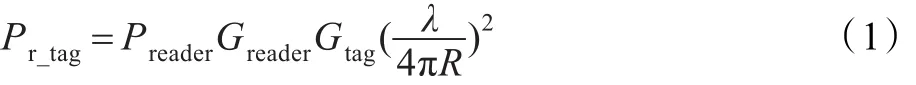
其中，Preader为阅读器发射功率，Greader为阅读器天线增益，Gtag为标签天线增益，λ为工作波长，R为阅读器到标签的距离。而在标签到阅读器的无线链路中（反向链路），对于无源UHF RFID系统，该链路为反向散射链路，当阅读器发射和接收采用同一天线时，根据雷达模型则阅读器的接收功率Pr_reader计算公式可表示为：

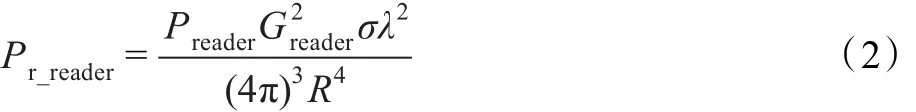
其中，σ为标签的雷达截面。

2.2 多径环境下的无源UHF RFID传播模型

综合考虑RFID实际应用环境，通过修改Friis自由空间传输方程，则前向链路中标签的接收功率Pr_tag可以表示为：

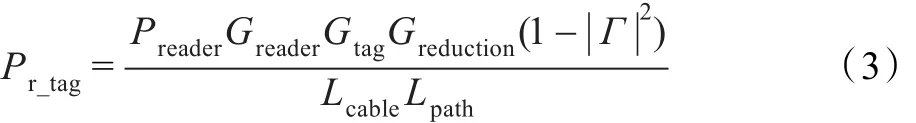
其中，Greduction用来描述由于天线失谐、标签附着材料和其他干扰因素等所引起的增益缩减，Γ为标签的反射系数，Lcable为线路损耗，Lpath为系统的路径损耗。标签的反射系数Γ可以用式（4）表示：

其中，ZA为天线的输入阻抗，ZL为负载阻抗。

在反向散射链路中，通过修改单站雷达方程，则阅读器的接收功率Pr_reader可以表示为：

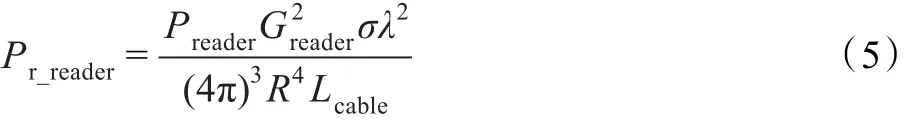
通常，标签的雷达截面可以分解为结构模式和天线模式。结构模式独立于天线负载，而天线模式与负载有关，因而，反向散射功率的结构模式部分不可以被调制，调制的反向散射信号与雷达截面的天线模式部分成比例关系[10]。而标签的雷达截面可以表示为标签增益及其反射系数的函数：

其中，Γdiff为标签的差分反射系数，Γdiff=Γ1-Γ2，Γ1和Γ2分别为标签芯片在不同状态下的反射系数，其大小取决于芯片负载情况[11]。由于标签天线的增益和阻抗与附着的材料相关，可以通过考虑天线增益和阻抗的变换来引入增益缩减系数Greduction。此外，由于材料的影响，实际环境中的反射系数相对自由空间定义的反射系数将发生变化，该变化包含在增益缩减中，Greduction可以表示为[12]：

其中，Gtag_material为考虑附着材料影响的标签增益，Gtag_free为自由空间下的标签增益。考虑到上述参数分析，则阅读器的接收功率Pr_reader可以进一步修改为：

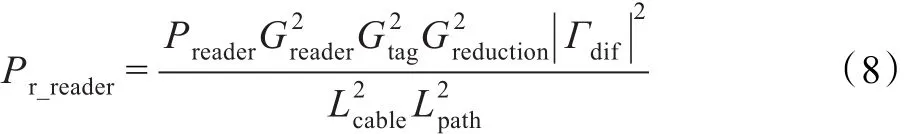
从式（3）和式（8）中可以看出，路径损耗Lpath为系统模型的关键参数，基于此，下面综合无源UHF RFID系统的实际应用环境和各种多径条件来分析讨论该参数。

3 路径损耗计算方法

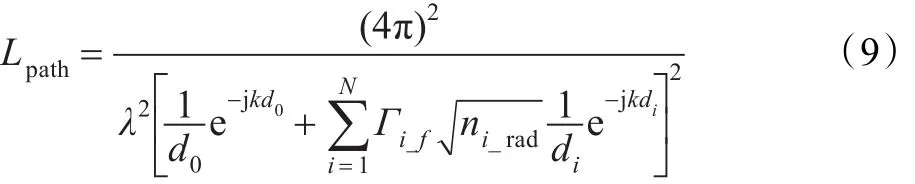
尽管大部分RFID是LOS通信系统，但环境反射的影响在应用中必须加以考虑。式（3）和式（8）中的路径损耗可以通过对地面、墙壁或其他物体的反射波建模来获取，路径损耗Lpath可以表示为：其中，d0为直接路径的长度，di为第i条反射路径的长度，k为波数，N为反射路径的总数，ni_rad为归一化天线散射模式，Γi_f为第i个波的菲涅耳反射系数。考虑到阅读器天线增益与方向性相关，Γi_f可以用式（10）来表示[13]：

其中，εc为地面的复介电常数，θi为入射角，p为极化相关因素，水平极化时p=1，垂直极化时p=1/εc。

当仅考虑直接路径时，该模型简化为自由空间模型。考虑一个仅包含直接射线和地面反射的简单模型。对于典型的地面参数（介电常数εr=15，电导率σc= 0.005 S/m）和典型的天线离地高度（0.5～2 m），菲涅耳反射系数Γf几乎是实数，最坏情况是Γf=-1。在平地模型中，当系统的识别距离R远大于阅读器天线离地高度(h1)和标签天线离地高度(h2)，即R>>4h1h2/λ时，路径损耗可以简化为：

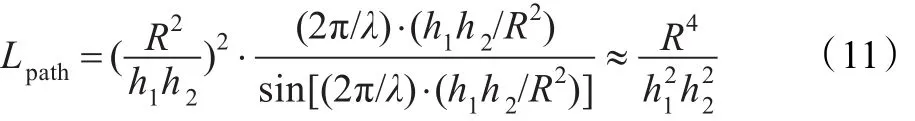
根据这些假设，对于平地模型，其路径损耗指数因子（或系数）n=4。通常，n的取值主要取决于应用环境。然而，在RFID实际应用环境中，这些假定存在偏差，因为实际距离往往小于开启距离Rtag，其路径损耗指数因子不同于自由空间(n=2)和平地模型(n=4)。在类似波导环境中，电磁波只沿一个方向传播，路径损耗可以通过距离的指数形式来描述。通常，RFID室内环境中的路径损耗计算可以根据经典的双斜率模型[14]获得：

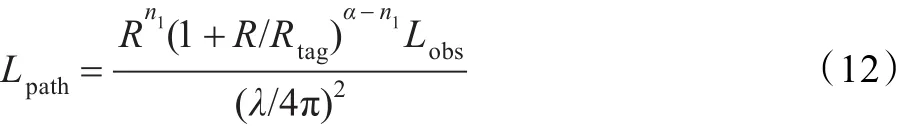
其中，n1为距离小于Rtag时的路径损耗系数，α为距离大于Rtag时的路径损耗系数，如平地模型α=4，Lobs为衍射和介质衰减所引起的损耗。而包含在Lobs中的衍射损耗可以通过移动通信广泛使用的刀口模型来获取，根据文献[15]可以导出Lobs的表达式：

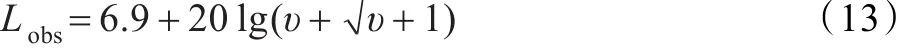
其中，υ＞-0.7，υ为障碍物的归一化高度，其计算可以通过式（14）给出：

其中，hobs为直接路径和障碍物边缘之间的距离，d1为障碍物边缘到阅读器的距离，d2为障碍物边缘到标签的距离。鉴于实际应用中的无源RFID系统识别距离往往小于开启距离Rtag，则式（12）可以简化为：

4 多径传播环境对系统性能的影响分析

图1描述了前向链路的多径情况：图1（a）是包含直接路径（LOS）的多径信道情况；图1（b）是小尺度衰落（快速衰落）情况，该多径信道无直接路径，标签接收来自地面和标签周围物体反射与衍射的功率；图1（c）是大尺度衰落（慢速衰落）情况，属于多反射与多衍射信道，标签接收到的信号为远离标签障碍物的多重反射和多重衍射之和，与第二种情况相反，这些多重路径经历不同的时间延迟，此外，阅读器和标签之间的主要障碍物会引起大尺度衰落（也称阴影衰落）。因此，路径损耗随识别距离急剧增大，以平均值为中心呈对数正态分布。第二种情况称为小尺度衰落，它是指由于位置的微小变化而引起的信号幅度及相位的变化。慢衰落可以用分贝表示，将其增加到Lpath中来表示未知的总路径损耗。由于标签的接收功率是一个随机变量，快衰落的影响可以通过总的接收功率（随机变量）而不是路径损耗来建模。

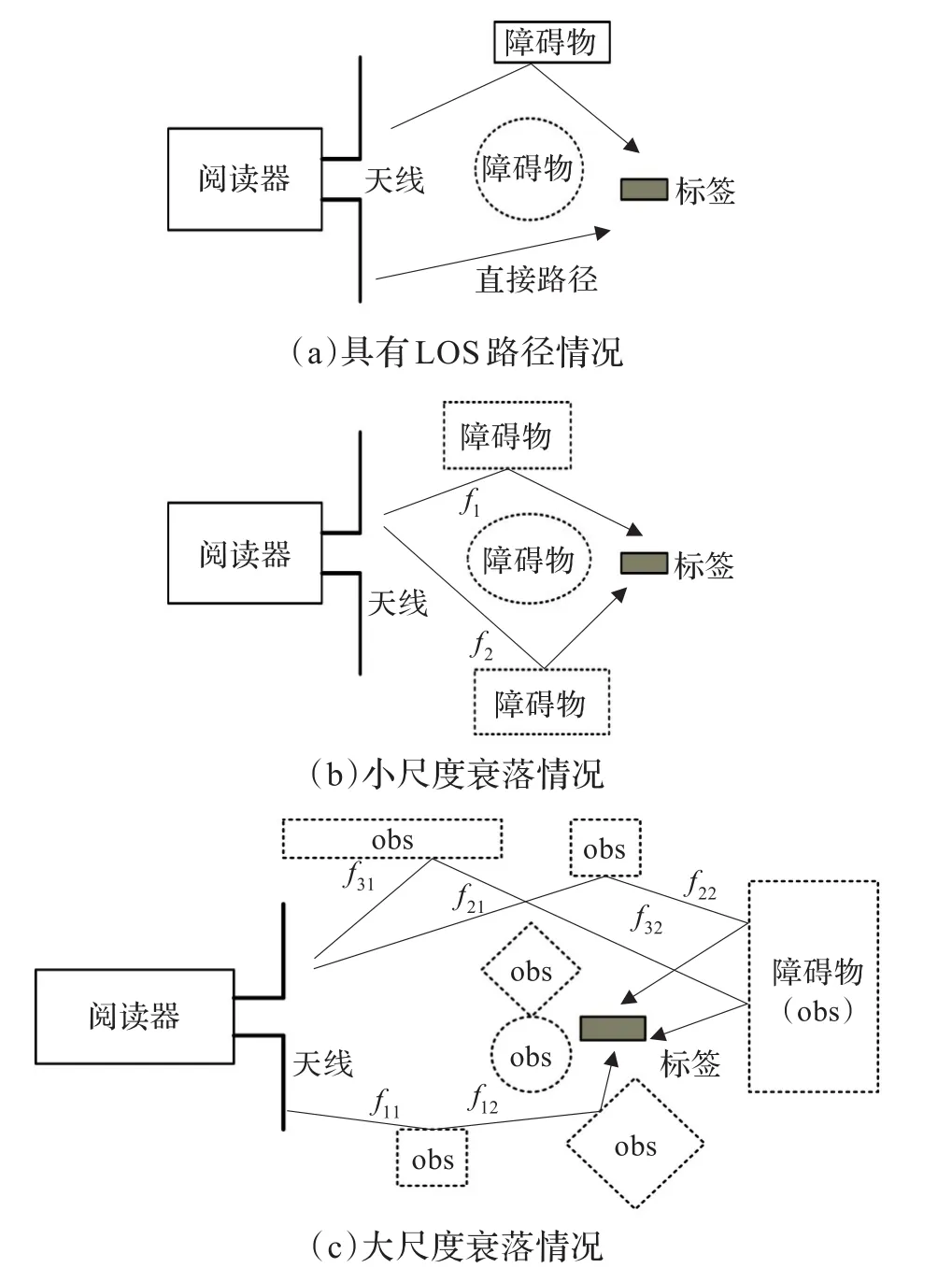
图1 前向链路各种多径情况

首先分析快速衰落情况，离散信道的低通脉冲响应hc(τ，t)可以通过若干个具有特定延迟和衰减的离散路径来表征。许多向量遭到破坏或重构导致了信号衰落。阅读器和标签间不同传播路径的杂波程度产生随机阴影影响，该随机变量通常具有正态分布。与此相反，当多径传播环境中LOS波占主导地位时，信号包络线的振幅服从莱斯概率分布[16-17]。在快速衰落情况中，标签接收功率大于开启功率Pth的概率可以由下列互补分布函数给出：

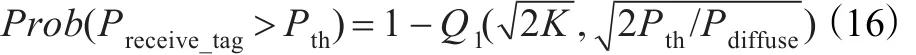
其中，Q1为马库姆函数，莱斯系数K定义为LOS镜面反射功率Plos与多径漫反射功率Pdiffuse之比。K值越大，则LOS链路则越多。

在近LOS链路中，由于来自物体的多重反射信号和其他拓扑特征的变化，接收功率强度随时间和空间发生变化。接收信号强度的变化量取决于非视距（NLOS）的程度。因为需要额外的发射功率来保证特定电平的可用性（定义为检测标签的概率），所以，当天线接收到的信号电平低于预定电平时，通信则发生中断。由于发射功率（即有效全向辐射功率，EIRP）受限于RFID法规，所以，该额外功率是很小的。因此，在非视距链路中提高可用性的关键是空间分集。如果没有主导LOS波存在，即Plos=0或K=0，则可以通过增加大量独立场分量来获得hc(τ，t)，然后，hc(τ，t)被建模为一个零均值高斯过程，任何时间的包络|hc(τ，t)|服从瑞利分布[18]。对于NLOS下的单输入单输出信道，随机接收信号电平服从瑞利分布。标签的平均接收功率大于其开启功率的概率可以用式（17）来表示：

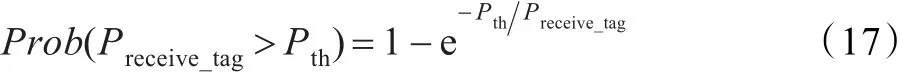
在移动通信系统中，慢衰落可以解释为大尺度内的快衰落平均水平。而RFID应用环境不同于移动通信环境，由于其散射体的距离较低，所以该大尺度必须缩减[19]。正如前面所讨论的，在RFID大部分应用中，由于LOS周围存在各种物体的阻挡，使得RFID环境为近LOS情形。RFID发射信号在到达接收端之前不是单一的散射机制，而是需要经过多次反射、折射、衍射和散射。假定不存在LOS路径，则接收信号Sr(t)、可以用所有路径项的和来表示：

其中，ai为某个路径幅度系数，表示各反射或衍射系数的级联相乘，φit为相位，该相位与各路径的行程差（相对直接路径）、到达时间、波长和周围环境等因素相关。从而，幅度系数ai可以表示为：

其中，bij为瑞利分布随机变量，M为沿路径i的散射次数。这些多重散射会影响接收功率的平均值。功率的对数就是这些随机变量的总和，根据中心极限定理，该功率服从高斯正态分布，即对数正态分布。然后，标签的平均接收功率大于其开启功率的概率可以通过式（20）来求解[19]：

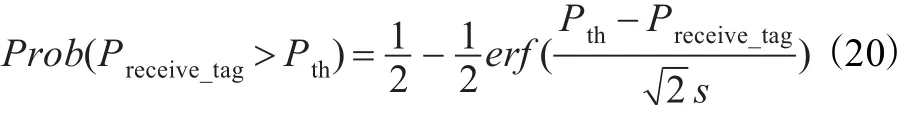
其中，erf(·)为误差积分函数，s为用分贝表示的功率标准偏差。功率延迟分布P(τ，t)显示标签天线的接收功率是不同路径到达时间的函数。可以从频率信道响应的傅里叶逆变换来获取脉冲信道响应hc(τ，t)，而P(τ，t)可以通过式（21）获得：

其中，τ为时间延迟，t为测量完成的时间点。若假定RFID是静态的，则遍历性条件满足，P(τ，t)的平均值等于瞬时值。

延迟分布决定了频率分散特性，也就是说，两个不同频率信道衰落的相关程度。从平均P(τ，t)中可以获得平均超量延时τm和均方根时延扩展τr。τr是反射延迟的均方根或标准偏差，它可以通过式（22）获取：

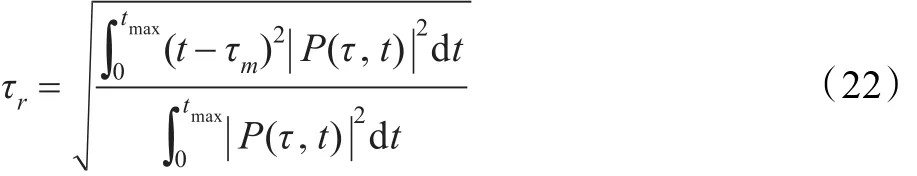
在一个高速数字系统中，该分散将经历频率选择性衰落和码间干扰。典型UHF RFID应用中，码持续时间通常大于10倍τr，所以不会产生严重的码间干扰。

另外一个重要的信道参数是相干带宽Bcoh，定义为组件之间的自相关函数首次低于预定水平（通常为最大值的0.3倍）时的频率间隔[14]。相干带宽可以从实际测量中近似获得：

基于上述关键参数分析，实际环境下的无源超高频RFID系统应用模拟思路可以描述为：①通过式（3）和双斜率模型来计算每一个点的平均功率；②利用式（20）来计算近NLOS对数正态环境下的覆盖概率；③用式（16）或（17）来分别计算莱斯或瑞利信道模型中的概率。

5 结果分析

基于平地模型，根据式（9）和（10），选择离地高度相同的阅读器天线和标签天线，路径损耗和识别距离的关系如图2所示。

从图2中的仿真和测量结果可以看出，与自由空间模型相比，平地模型更接近实际，并且其对路径损耗的预测值大于测量值。由于阅读器天线带宽减少了直接和反射波束的局部消除，所以一些具有相似延迟路径的叠加引起预测与测量的偏差。尽管平地模型存在局限性，但其衰落位置的预测与测量基本保持一致。然而，对于更远的距离，需要考虑更多路径来描述大衰落。此外，衰落幅度与频率相关，对于不同的频带，最大和最小值的位置依赖于极化特性。因而，极化的多样性可以有效防止多径信道衰落。

根据式（12），对数标度上的双斜率模型阐明了路径损耗对应于一条斜率为n1的直线，该直线提供了随机路径损耗的平均值。这相当于通过散射路径损耗测量值拟合一条最小二乘线性回归线，使得回归线路径损耗的均方差最小化。从该回归中可以获得不同离地高度天线的路径损耗系数平均值n1，结果如图3所示。从图3中可以看出：平地模型预测的路径损耗系数仿真值要比实测值低；多径环境对较低离地高度天线影响较大，其路径损耗系数大于2，当天线离地高度增加时，其路径损耗系数则趋向于自由空间的损耗系数值2；也就是说，天线离地高度越低，对路径损耗的影响就越大。此外，相对垂直极化，水平极化的路径损耗系数曲线具有更多纹波。

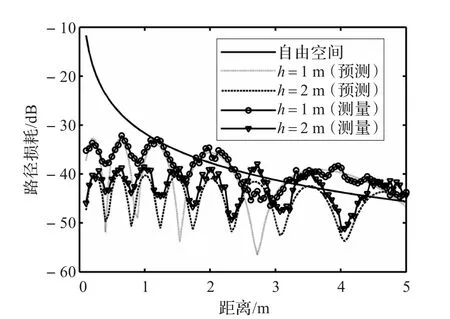
图2 路径损耗与识别距离及天线离地高度的关系

图3 路径损耗系数与天线离地高度的关系

图4显示了基于双斜率模型仿真计算与测量值之间的标准方差随天线离地高度变化的关系，两种极化的平均值接近2 dB，水平极化的方差要大于垂直极化的方差，这是因为对于水平极化来说，地面的反射系数是负的，其入射更接近正常地面入射。此外，可以通过图4获得功率标准偏差s。

图4 标准偏差与天线离地高度的关系

设定n1的值为2，标签天线增益为0 dBi，阅读器天线增益为6.0 dBi，EIRP采用FCC-15规定的4 W来预测RFID系统的识别范围。图5描述了标签和阅读器平均接收功率与识别距离的关系。考虑到典型的标签开启功率或灵敏度为-10 dBm左右，阅读器的灵敏度为-80 dBm左右，从图5中可以看出，影响RFID系统识别距离的通信链路主要是前向链路，即阅读器到标签的通信链路。

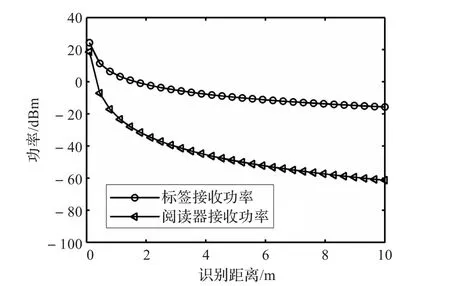
图5 平均接收功率与识别距离的关系

给定标签激活概率Prob(Preceive_tag＞Pth)=95%，根据式（3）、（16）、（17）和（20）可以得出RFID系统最大识别距离与有效全向辐射功率的关系如图6所示。从图6中可以看出，在EIRP一定的情况下，基于自由空间模型的识别距离最大，基于莱斯分布和瑞利分布的次之，而基于对数正态分布的识别距离与功率标准差s有关。

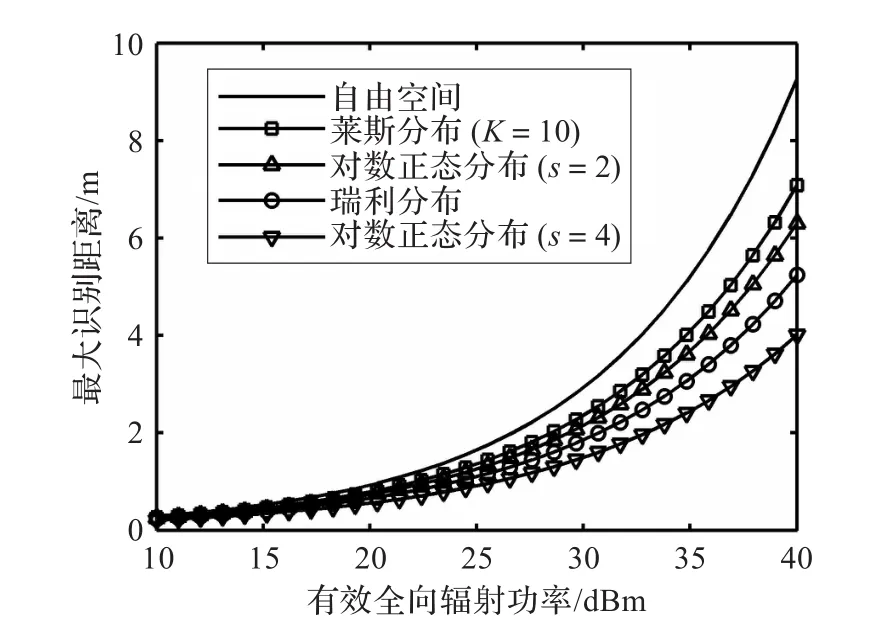
图6 不同多径信道的最大识别距离预测

该仿真结果显示，通过自由空间模型计算的识别距离过于理想，偏差较大，基于莱斯分布、瑞利分布和对数正态分布的识别距离预测值更接近实际。此外，当EIRP取值较小时，上述几种情况的差别不明显，当EIRP取值较大时，则有明显的差别。

6 结束语

基于自由空间和单站雷达模型，本文研究了多径传播环境下的无源超高频RFID电波传播模型，分析了多径传播环境对系统性能的影响。通过上述理论研究和实验仿真结果可以得出：（1）要正确地预测RFID系统识别距离，需要建立符合其实际应用环境的电波传播模型；（2）路径损耗是RFID无线链路预算中的关键参数，其计算方法取决于实际应用的多径条件；（3）鉴于阅读器的灵敏度远小于标签的开启功率，则影响RFID系统识别距离的通信链路主要是前向链路；（4）RFID应用环境不是静态的而是动态的，标签接收功率是一个随机变量，不同多径传播条件下的标签接收功率服从不同的统计概率分布。此外，基于多径传播环境下的电波传播模型，本文为无源超高频RFID系统提供一种新的应用模拟思路。

[1]BANSAL R.Com ing soon to a Wal-Mart near you[J].IEEE Antennas Propagation Magazine，2003，45（12）：105-106.

[2]唐志军，席在芳，詹杰.无源反向散射RFID系统识别距离的影响因素分析[J].计算机工程与应用，2012，48（23）：85-89.

[3]Nikitin P V，Rao K V S.Antennas and Propagation in UHF RFID systems[C]//IEEE International Conference on RFID，The Venetian，Las Vegas，Nevada，USA，2008：277-288.

[4]程鹏亮，戎蒙恬.射频识别系统电波传播模型与仿真[J].计算机仿真，2008，25（2）：322-324.

[5]Zhuo S，Cheung S C.Investigation of radio link budget for UHF RFID systems[C]//IEEE International Conference on RFID-Technology and Applications，Guangzhou，China，2010：164-169.

[6]Lazaro A，Girbau D，Salinas D.Channel modeling for UHF RFID[C]//Proceedings of the 39th European Microw ave Conference，Rome，Italy，2009：1105-1108.

[7]Raffaele D E.An indoor backscattering channel characterization for UWB passive RFID applications[C]//The 6th European Conference on Antennas and Propagation，Prague，Czech，2012：1169-1173.

[8]Daniel A，Ulrich M.Characterization and modeling of UHF RFID channels for ranging and localization[J].IEEE Transactions on Microwave Theory and Techniques，2012，60（5）：2491-2501.

[9]Nikitin P V，Rao K V S，Lam S F.Power reflection coefficient analysis for complex impedances in RFID tag design[J]. IEEE Transaction on Microwave Theory and Technologies，2005，53（9）：2721-2725.

[10]唐志军，何怡刚.无源射频识别系统中的雷达截面分析与计算[J].物理学报，2009，58（7）：757-763.

[11]Nikitin P V，Rao K V S，Martinez R D.Differential RCS of RFID tag[J].Electronics Letters，2007，43（8）：431-432.

[12]Griffin J D，Durgin G D，Haldi A，et al.RF tag antenna performance on various materials using radio link budgets[J].IEEE Antennas Wireless Propagation Letters，2006，5（1）：247-250.

[13]Antonio L，David G，David S.Radio link budgets for UHF RFID on multipath environments[J].IEEE Transaction on Antenna and Propagation，2009，57（4）：1241-1251.

[14]Rappaport T S.Wireless communication：principles and practice[M].2nd ed.Englewood Cliffs，NJ：Prentice-Hall，2001.

[15]LEE C Y.Mobile communications engineering[M].New York：McGraw-Hill，1995.

[16]佘开，何怡刚，李兵，等.无源超高频RFID系统链路预算分析[J].仪器仪表学报，2010，31（5）：974-979.

[17]Helstrom C W.Com puting the generalized M arcum Q-function[J].IEEE Transaction on Information Theory，1992，38（4）：1422-1428.

[18]Saleh A A M，Valenzuela R A.A statistical model for indoor multipath propagation[J].IEEE Journal on Selected Areas in Communications，1987，5（2）：128-137.

[19]Bertoni H L，Honchareko W，Rocha L，et al.UHF propagation for wireless personal communications[J].IEEE Proceeding，1994，82（9）：1333-1359.

TANG Zhijun1,WU Xiaofeng1,ZHAN Jie2,HU Shigang1,XI Zaifang1

1.School of Information&Electrical Engineering,Hunan University of Science and Technology,Xiangtan,Hunan 411201,China
2.School of Physics&Electronic Science,Hunan University of Science and Technology,Xiangtan,Hunan 411201,China

There is a deviation in predicting identification distance of the radio frequency identification system for free-space model,a radio propagation model for passive UHF RFID system s is proposed by taking into full consideration to the application of RFID system in multipath propagation environment.Main affecting factors and its calculation methods of path loss are analyzed emphatically for the forward link of passive UHF RFID system s.Furthermore,a simulated method of passive UHF RFID applications in the actual environment is presented based on the proposed propagation model.The simulated and measured results show that the identification distance of passive UHF RFID is predicted more accurately by using the proposed model.

radio frequency identification;propagation model;multipath environment;path loss;identification distance

A

TN926

10.3778/j.issn.1002-8331.1311-0316

TANG Zhijun,WU Xiaofeng,ZHAN Jie,et al.Radio propagation model for passive UHF RFID systems in multipath propagation environment.Computer Engineering and Applications,2014,50（16）：25-30.

国家自然科学基金（No.61377024，No.61274026，No.61376076）；湖南省教育厅科学研究项目（No.12A 045，No.12C0108）；湖南省科技计划资助项目（No.2013FJ2011）。

唐志军（1974—），男，博士，副教授，主要研究方向为RFID技术、物联网技术、超宽带天线、超低功耗微波器件等；吴笑峰，博士，副教授，主要研究方向为超大规模模拟集成电路、超低功耗微波器件等；詹杰，博士，副教授，主要研究方向为无线定位技术、射频天线等；胡仕刚，博士，副教授，主要研究方向为集成器件可靠性分析；席在芳，副教授，主要研究方向为宽带通信信号处理方法。E-mail：zjtang@hnust.edu.cn

2013-11-21

2014-03-12

1002-8331（2014）16-0025-06

CNKI网络优先出版：2014-03-19,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0316.htm l